基于分段线性非饱和随机共振的机械早期故障诊断方法研究
2017-09-11段佳雷
段佳雷
(西安工程大学,陕西西安710600)
基于分段线性非饱和随机共振的机械早期故障诊断方法研究
段佳雷
(西安工程大学,陕西西安710600)
针对大型机械设备运行环境恶劣、故障特征难以提取的问题,提出一种基于分段线性双稳态势函数模型的非饱和随机共振方法。该方法通过分段线性化的势函数代替经典的双稳态势函数,然后利用频移尺度变换实现机械设备振动信号的小参数化,使其满足随机共振系统的输入条件;最后,将系统输出信号的信噪比作为遗传算法的目标函数,优化非饱和随机共振系统参数,实现机械设备早期故障特征的增强与提取。仿真分析表明该方法可以有效地提取淹没在强噪声背景下的微弱故障冲击特征,而且轴承实验证明提出的方法能够有效增强与提取故障特征频率。仿真与实验结果进一步表明提出的方法优于经典双稳态随机共振方法,不仅能够获得高的输出信噪比,而且在特征频率处具有更高的幅值。以上优点归功于提出方法不仅克服经典双稳态随机共振系统的内在输出饱和问题,而且利用遗传算法实现系统与输入信号之间的最佳匹配。
非饱和随机共振;故障特征提取;信噪比;早期故障诊断
0 引言
随着科学技术的发展,机械设备朝着高、精、尖方向发展,致使设备结构愈来愈复杂,而且其恶劣的运行环境,导致故障特征遭受传递路径影响极其微弱,通常被淹没在强背景噪声中,因此机械设备故障难以提取与诊断。于是,早期故障特征提取一直是大型机械设备故障诊断中的关键难题[1-2]。
信号处理作为故障特征提取的一把利器,广泛应用于机械故障诊断。然而,大多数信号处理方法以消除信号中的噪声为目的,从而实现早期故障特征的提取[3];而意大利学者Benzi等[4]发现的随机共振方法能够利用噪声实现微弱特征的增强与提取,从而广泛应用于通信信号处理[5]、图像增强[6]、机械故障诊断等[7]领域。焦尚彬等[8]应用经典双稳态随机共振,实现了多频微弱特征的增强与提取;潘峥嵘等[9]基于经典双稳态随机共振系统输出信号的符号序列熵指标作为优化算法的目标函数,实现了轴承早期故障诊断;Lei等[10]基于频移尺度变换利用经典双稳态随机共振方法实现了行星齿轮箱太阳轮断齿、缺齿的故障类型判别;Klamecki[7]利用经典双稳态随机共振增强与提取旋转机械的故障特征;Barbini等[11]基于耦合的经典双稳态随机共振系统,实现了噪声的再次利用和微弱正弦信号的深度增强与提取;Qiao等[12]表明经典双稳态随机共振系统存在内在饱和问题,从而限制了随机共振的增强性能,为了解决该问题,通过对经典双稳态势函数的势阱壁进行线性等效,扩展了粒子运动路径,并基于该模型提出了非饱和随机共振方法实现了轴承和齿轮箱的故障诊断。
综上所述,已有随机共振方法主要聚焦在经典随机共振的改进和应用上,其经典双稳态势函数的陡峭势阱壁限制了布朗粒子的运动路径,致使系统输出陷入局部饱和状态,从而使经典双稳态随机共振系统的增强性能受限。受到文献[12]的启发,针对这一问题,建立了一个新的分段双稳态势函数模型,并基于绝热近似理论推导了其输出信噪比表达式;其次,基于建立的模型提出了非饱和随机共振新方法,该方法利用遗传算法优化非饱和随机共振的系统参数,获得最佳随机共振系统并实现机械早期故障特征的增强与提取。仿真和实验结果表明,提出的方法优于经典随机共振方法,能够获得较大的输出信噪比而且在故障特征频率处拥有更高的幅值。
1 经典双稳态随机共振
受随机噪声和周期外力激励的布朗粒子在经典双稳态势阱中的跃迁运动可以由郎之万方程描述[13]为
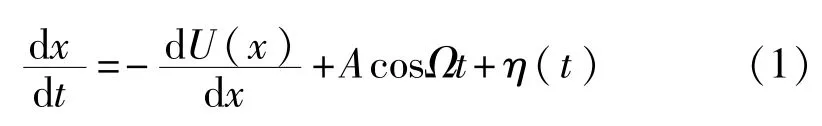
其中A,Ω分别表示微弱周期信号的幅值和角频率;η(t)是高斯白噪声,且满足以下统计特性:
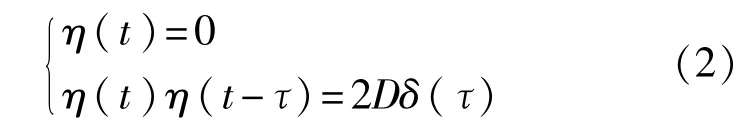
其中D是噪声强度。U(x)是经典双稳态势函数:
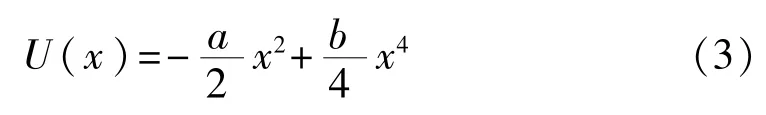
其中a和b都是大于0的系统参数。
为了直观地解释经典双稳态随机共振系统的输出饱和问题,当a=b=1时图1给出了在不同输入信号幅值A情况下经典双稳态随机共振系统的输出,可以看出随着系统输入幅值A的增加,系统输出信号的幅值变化缓慢,逐渐陷入局部饱和状态,表明经典随机共振系统的增强能力遭受经典双稳态势函数的陡峭势阱壁限制。因为陡峭的势阱壁使布朗粒子运动到某侧势阱壁时受到较大的反向势力,促使粒子快速向另一侧势阱壁运动,如此往复,则布朗粒子的运动路径被完全限制在势阱的局部范围内,难以实现较大幅度的跃迁。
2 分段非饱和双稳态随机共振
受文献[12]的启发,为了进一步避免经典双稳态随机共振的输出饱和问题,经典双稳态势函数被线性化为分段双稳态势函数:
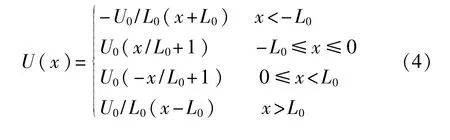
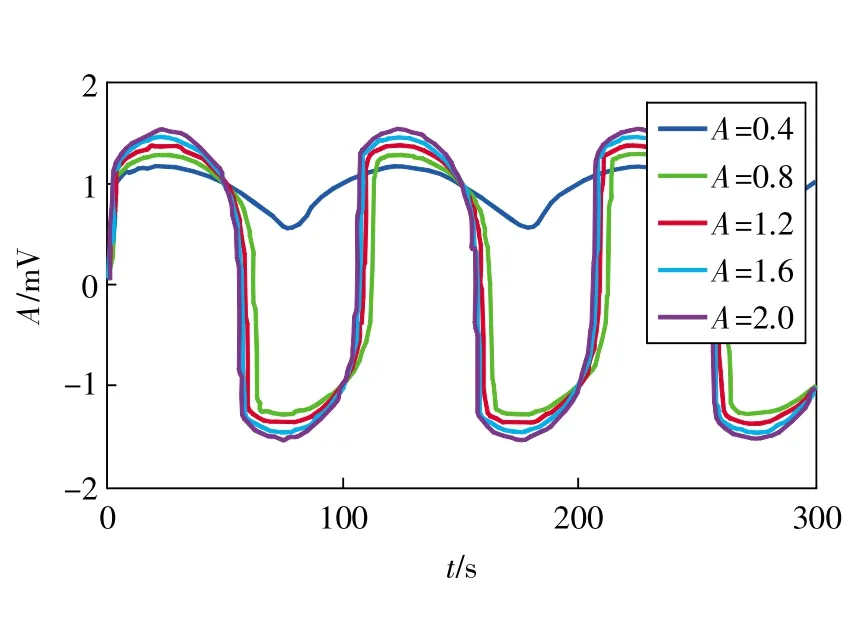
图1 经典双稳态随机共振系统的输出信号
式中:x——系统响应,其本质是布朗粒子在随机力η(t)和周期外力AcosΩt激励下,在势函数U(x)中的运动轨迹;
U0、L0——分段双稳态随机共振系统参数,且其均大于0。
为了合理对比,取U0=L0=1使得分段双稳态势与经典双稳态势具有相同的阱宽和垒高,图2呈现了在不同幅值的周期激励下分段双稳态随机共振系统的输出信号,可以看出随着周期激励的幅值逐渐增加,分段双稳态随机共振系统输出信号的幅值成倍放大。对比图1与图2可以发现分段双稳态随机共振系统具有更好的信号增强与放大能力,不会陷入饱和状态。这是因为分段双稳态势函数具有线性化的势阱壁,随着系统输入的增大,势阱壁的陡度保持为±U0/L0,且其与系统响应x的变化无关;相反由于经典双稳态势中x4的存在,当系统响应x>1时经典双稳态势的势阱壁的陡峭度成倍增大,致使粒子运动陷入局部饱和状态。
假设ρ(x,t)是分段双稳态随机共振系统响应x的统计概率密度函数,则分段双稳态随机共振系统对应的福克-普朗克方程[14]为
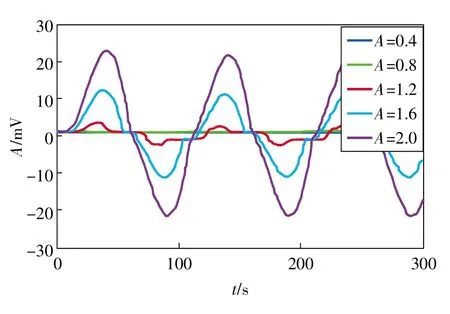
图2 分段双稳态随机共振系统的输出信号
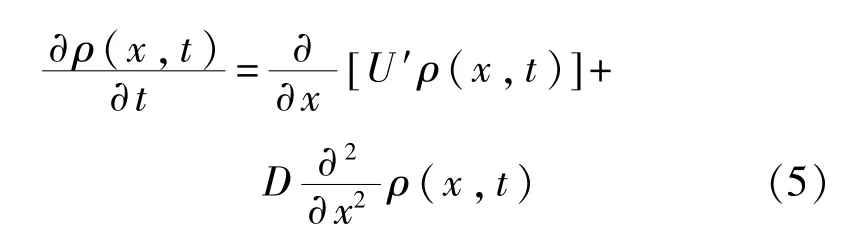
假定初始的概率分布满足绝热近似理论,即假定t=0时刻概率分布集中于某一势阱时:
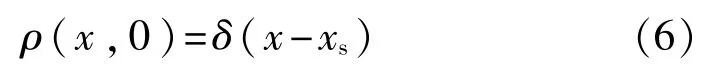
式中xs=L0是势函数U(x)的极值点。
假设概率流不随时间变化,即∂ρ(x,t)/∂t=0,对方程式(5)进行积分可得稳定解:
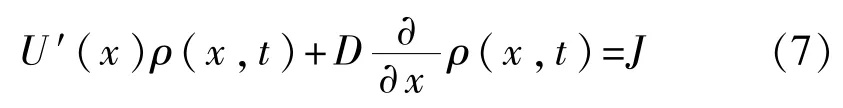
其中J表示定态流的强度。对于式(7),它的定态解为
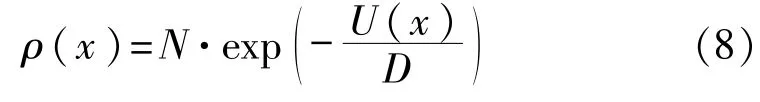
式中N为归一化常数。
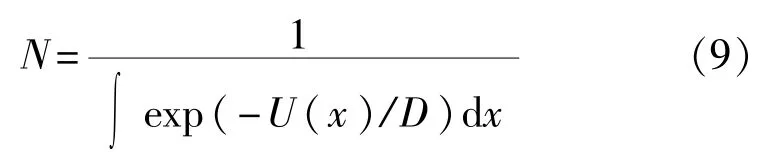
同理,式(5)的齐次解为
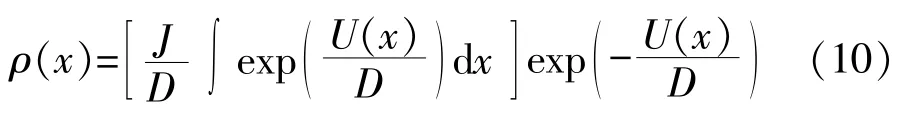
取ρ(x,t)=N·exp(-U(x)/D),则得:
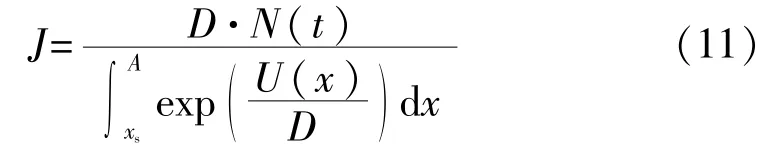
那么在t时刻处于(-∞,A)区间内的总概率为

由于J为概率流出这一区域的速率流,所以在稳态下,再结合式(11)得到:
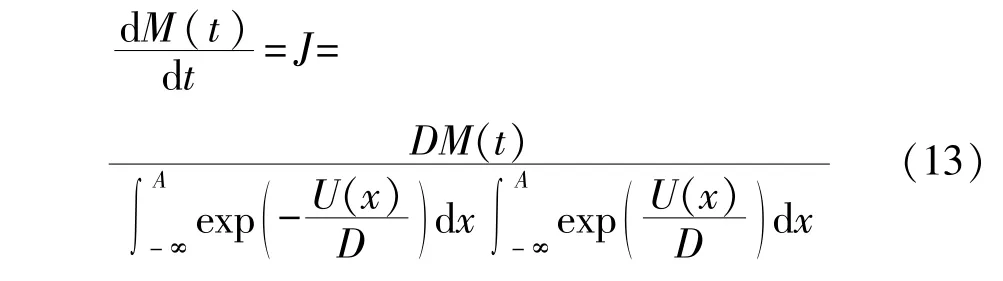
式中M(t)=M(0)exp(-Rt),而且:
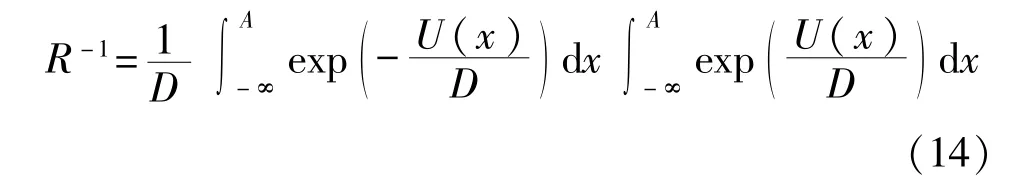
式中R表示概率流入不稳定区的速率,该速率被称为Kramers逃逸速率[15]。由于D〈〈1,式(14)中的两个积分均可求出,前一积分的贡献主要来自稳定点的邻域,而后一积分的主要贡献来自不稳定点的邻域。因此,分段线性系统中两势阱之间的概率跃迁速率为
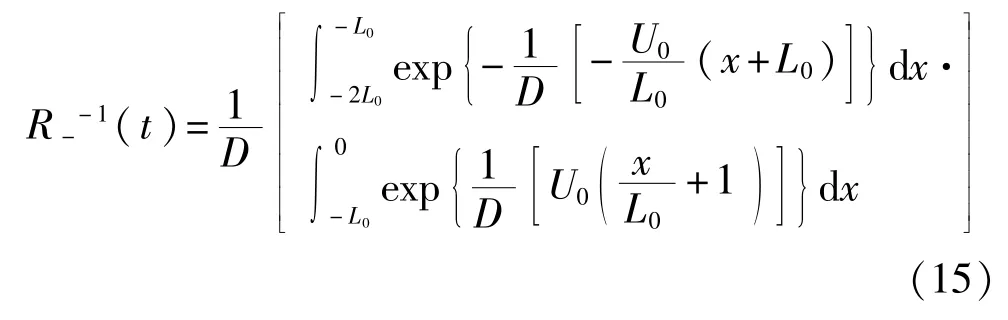
在A〈〈1,D〈〈1的条件下,可以求得:
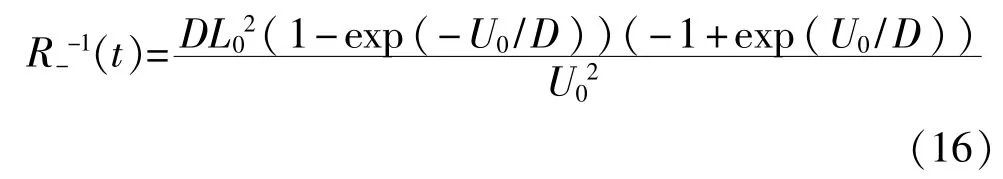
分段双稳态势函数具有对称性,故R--1(t)=R+-1(t),从而分段双稳态随机共振系统的Kramers逃逸速率为
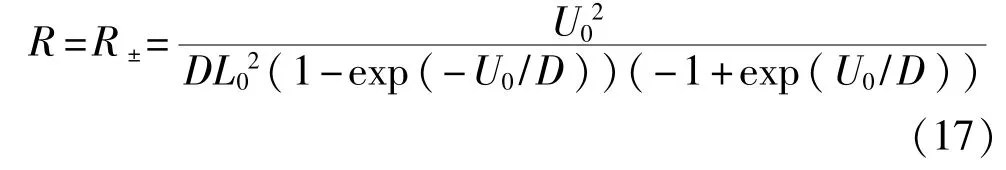
通常采用输出信噪比SNR来衡量系统的随机共振效果,其定义为输出噪声功率与信号功率之比。因此分段双稳态随机共振系统输出信噪比表达式为
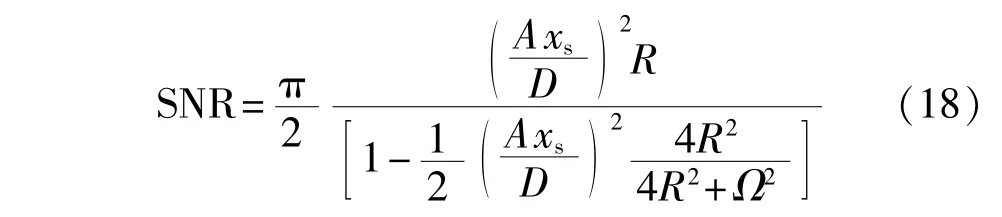
图3展示了分段双稳态随机共振系统输出信噪比与周期激励力幅值、系统参数以及噪声强度之间的关系。从图3(a)可以看出,随着噪声强度的增加,输出信噪比呈现单峰结构,这一特点表明了随机共振现象的发生。此外,较大的周期激励力幅值有助于系统输出信噪比的改善。而图3(b)和图3(c)呈现了输出信噪比与系统参数L0和U0之间的关系,可以发现通过调节系统参数能够控制随机共振系统的输出,从而最佳地增强微弱信号或机械早期故障特征,这是因为系统参数决定了势垒的高度和势阱的宽度,而这些参数决定了周期外力与噪声之间的协同程度。
基于以上理论分析,提出了一个分段线性非饱和随机共振机械故障诊断方法,具体步骤如下:
1)信号预处理。由于轴承等故障特征通常受转速信息的调制,因此希尔伯特变换被用于解调故障信号,求取相应的包络信号。然后,采用频移尺度变换压缩求得的包络信号,使其满足随机共振的小参数输入条件。
2)目标函数计算。将步骤1)中经过频移尺度变换后的包络信号输入分段双稳态随机共振系统,并利用四阶龙格库塔方法求解郎之万方程,获得随机共振系统的响应,依据式(19)计算系统输出信噪比作为遗传算法的目标函数[16]。
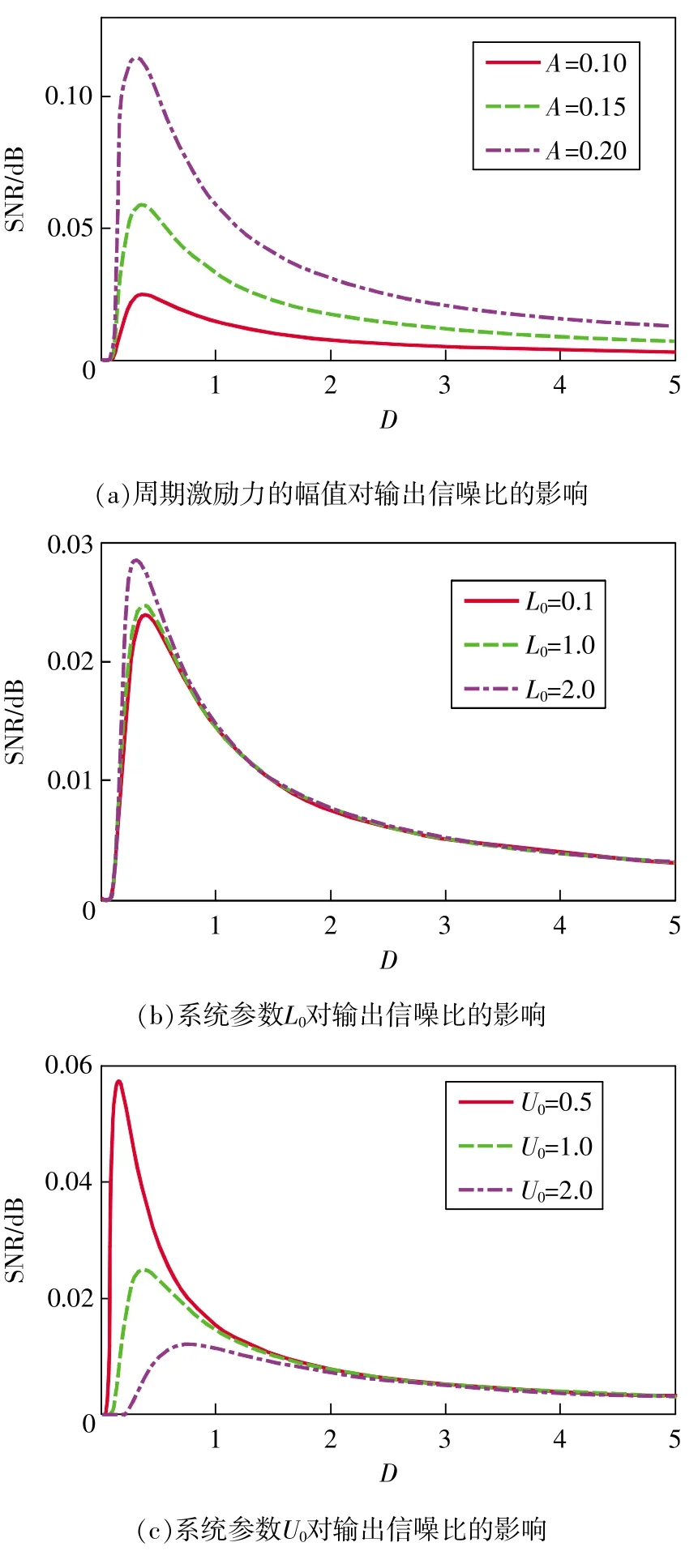
图3 分段双稳态随机共振系统输出信噪比与周期激励、系统参数之间的关系
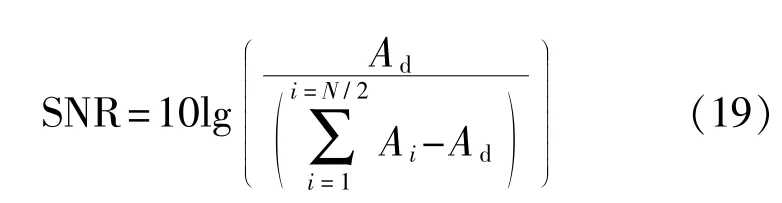
式中:Ad——分段双稳态随机共振系统输出信号在特征频率处的幅值;
Ai——输出信号频谱中每根谱线的幅值;
N——系统输入尺度变换后包络信号的长度。
3)优化更新。初始化系统参数的搜索范围为L0∈(0,10]和U0∈(0,10],并初始化遗传算法参数,具体参见文献[17]。依据每个搜索节点的信噪比大小进行更新、优化,最终将公告板最佳记录输出,即最佳输出信噪比SNRbest和最佳系统参数对(L0,U0)best。
4)机械故障特征提取。将最佳系统参数对(L0,U0)best代入分段双稳态随机共振系统形成最后的优化系统,并将移频尺度变换后的机械故障振动信号包络输入该优化系统,利用四阶龙格库塔算法求解该分段双稳态随机共振系统的输出信号,对该输出信号进行傅里叶变换提取微弱特征,并实现机械设备的早期故障特征提取。
3 仿真分析
为了验证提出方法的有效性,一个频率65 Hz、冲击幅值为1的单边衰减冲击信号被淹没在的高斯白噪声中,采样频率为10kHz,采样时间为1s。图4(a)给出了冲击特征和噪声混合信号的时域波形,可以看出模拟的轴承外圈故障冲击特征被强噪声所淹没,难以辨别;图4(b)和图4(c)分别展示了该混合信号的频谱和包络谱,从频谱可以看出在1 000 Hz频率处存在微弱的共振频带,而包络谱中很难发现65Hz故障特征频率。同时,根据信噪比公式(19)计算得到其包络信号的信噪比为-28.9764dB,可见信噪比极低。
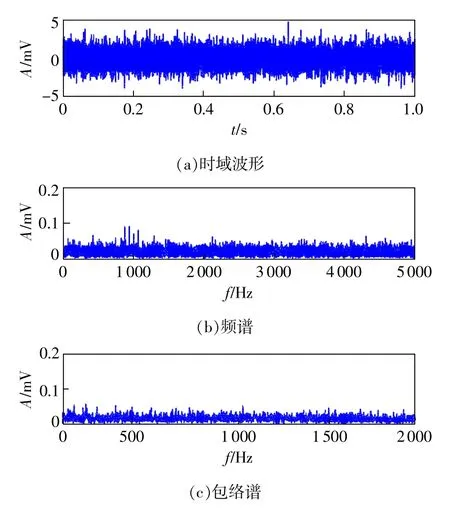
图4 待检混合信号
首先,经典双稳态随机共振方法被用于处理图4(a)所示的混合信号,设置高通滤波器的通带截止频率和阻带截止频率分别为56Hz和60Hz,频移尺度变换的频移因子为56 Hz,尺度因子为200,压缩后的特征频率为(65-56)/200=0.045〈〈1 Hz,满足绝热近似下随机共振的小参数限制。利用遗传算法优化得到的最佳增强与提取结果如图5所示,可以看出特征频率65Hz在整个频谱中被突出,而且时域特征具有明显的周期特性。但是,在时域波形和频谱中仍然存在很强的噪声干扰,计算得到特征频率幅值和增强后信号的信噪比分别为0.07352mV和-15.3735dB。此外,在特征频率65Hz周围存在很强的噪声干扰频率。
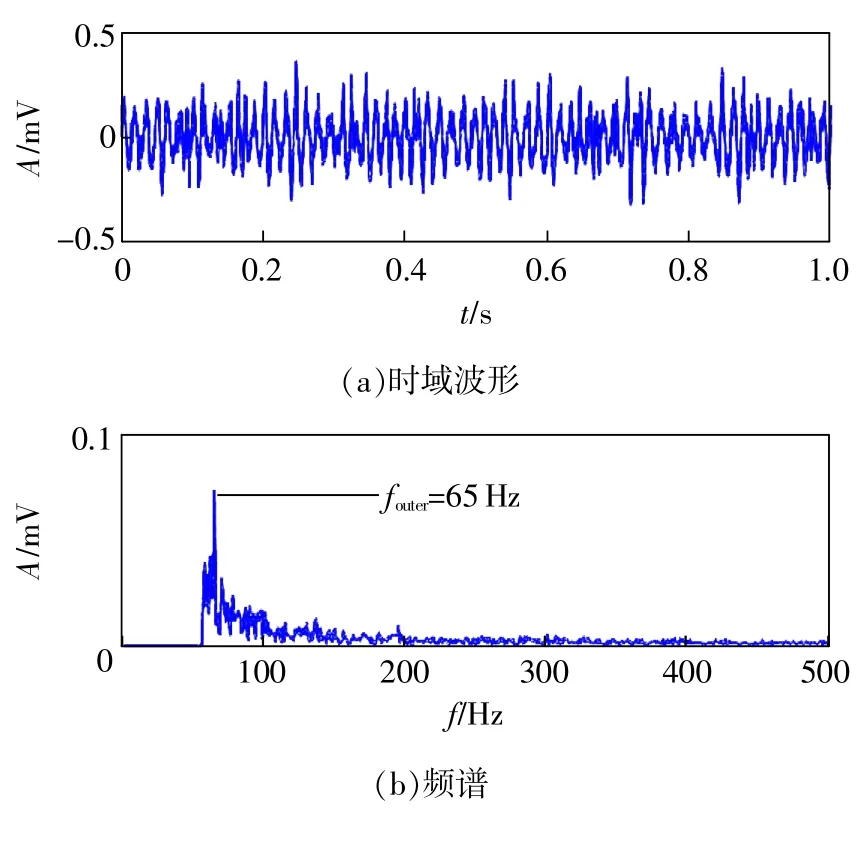
图5 经典双稳态随机共振方法的增强提取结果
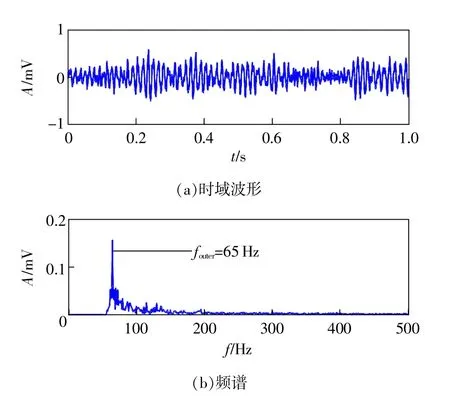
图6 提出的分段线性非饱和随机共振方法的增强提取结果
同样,当L0=0.0983,U0=0.0218时获得最佳的分段线性非饱和随机共振方法增强与提取结果如图6所示,可以看出噪声基本被消除,时域波形具有明显的周期特性,而且频谱中特征频率65Hz完全在整个频谱中处于主导地位,干扰频率幅值非常微弱。输出信号特征频率的幅值和信噪比分别为0.1574mV和-12.9449dB。对比两种方法的增强结果,可以看出提出的方法不仅在特征频率处获得了最大的幅值,而且也获得了较高的输出信噪比,同时在特征频率65Hz周围有较少的噪声干扰频率。这一结果归功于分段线性双稳态势函数克服了经典双稳态势的内在饱和特性,从而能最大程度地增强与提取故障特征频率。
4 实验验证
滚动轴承作为旋转机械的重要部件之一,其故障信号表现出典型的微弱冲击特征,且通常被强烈的背景噪声所淹没,难以检测与提取,尤其是轴承外圈极易发生损坏。因此,凯斯西储大学轴承实验数据[1]被用于验证提出的分段线性非饱和随机共振机械故障诊断方法。采用采样频率为48kHz,采样时间为2 s,轴承转速为1 750 r/min的驱动端深沟球轴承外圈故障数据验证提出方法的有效性,其故障大小为0.007in(1in=2.54cm),根据轴承参数计算得到外圈故障特征频率的理论值为fouter=104.5567Hz。含有噪声强度为6的轴承外圈故障振动信号的时域波形、频谱、包络谱如图7所示,可以看出在图7(a)中时域波形被强噪声所淹没,很难发现周期性冲击,而在图7(c)的包络谱中可以看到微弱的轴承外圈故障特征频率fouter=105Hz,与理论值相差0.4433Hz小于频率分辨率0.5 Hz,因此105 Hz是实际轴承外圈故障特征频率,但是在整个频谱中显得比较微弱,且周围分布较多的噪声干扰频率,难以判定是否发生早期故障,若判定无故障,可能导致漏诊,甚至造成重大事故。
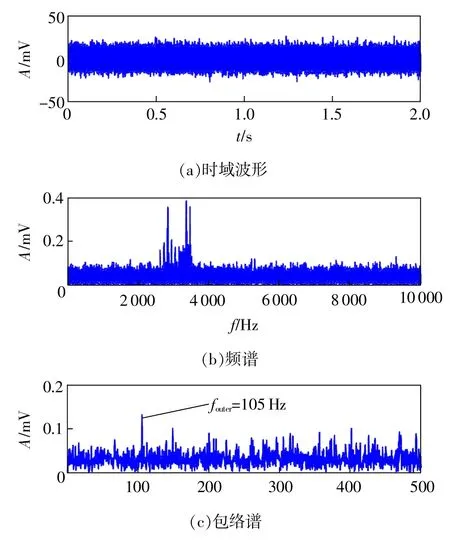
图7 含噪轴承外圈故障信号
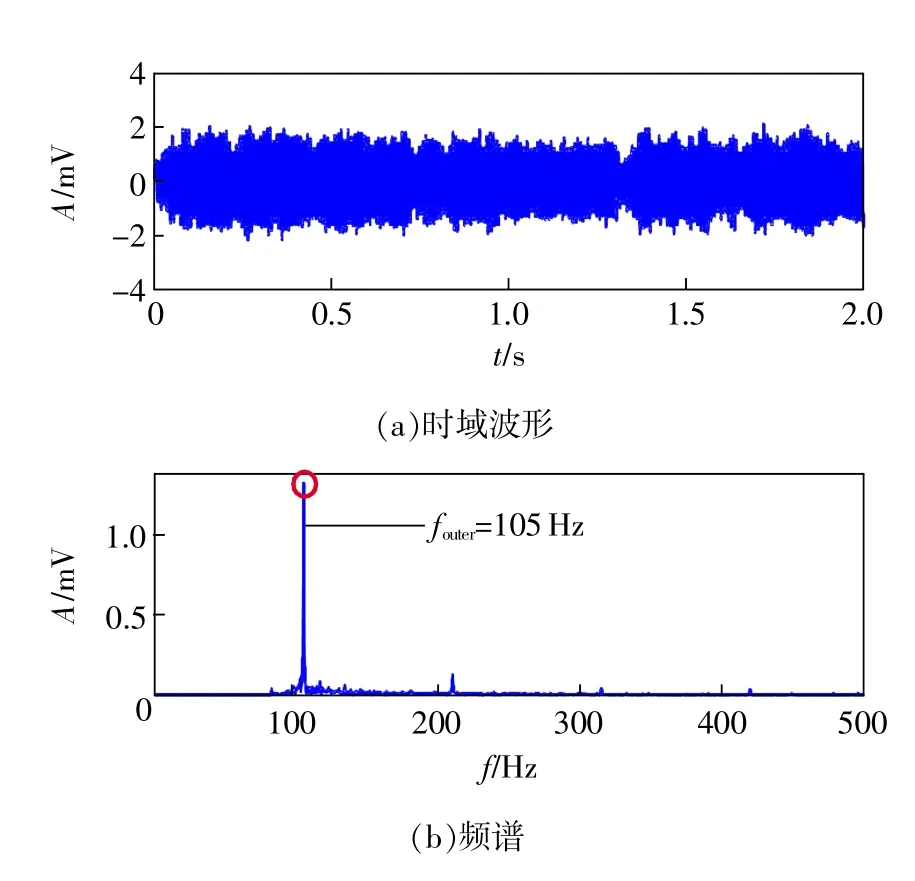
图8 提出的分段线性非饱和双稳态随机共振方法增强提取结果
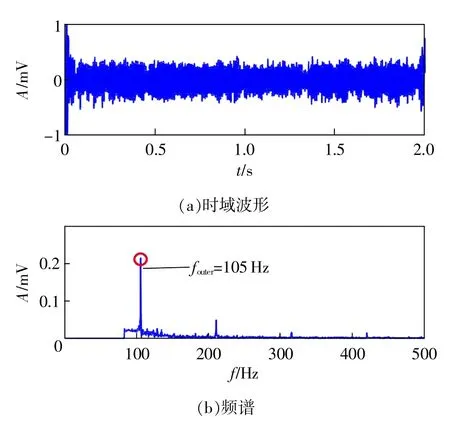
图9 经典双稳态随机共振方法增强提取结果
首先,高通滤波器的通带截止频率和阻带截止频率分别为82Hz和100Hz、频移因子为82、尺度因子为200,利用提出的分段线性非饱和双稳态随机共振方法处理图7的含噪轴承故障信号,其随机共振系统输出信号的时域波形和频谱分别如图8(a)和图8(b)所示。可以看出,频谱中有清晰的轴承外圈故障特征频率105Hz,而且其在整个频谱中占主导地位,增强与提取结果在故障特征频率处的幅值和信噪比分别为1.322mV与-10.0590dB。为了对比,同样地经典双稳态随机共振方法被利用处理图7的轴承外圈故障信号,其增强结果的时域波形和频谱分别如图9(a)和图9(b)所示。从频谱图可以看出,轴承外圈故障特征频率在整个频谱中被突出,但周围存在较小的噪声干扰频率,其增强提取结果在故障特征频率处的幅值和信噪比分别为0.2143mV与-15.0849dB。对比增强提取结果可以发现,提出的分段线性非饱和随机共振方法在故障特征频率处具有更高的幅值,而且具有更高的输出信噪比。这是因为提出的分段线性非饱和随机共振方法克服了经典随机共振方法的内在饱和问题,展现出更好的增强能力。轴承外圈故障实验进一步证明了提出方法的有效性。
5 结束语
随着机械设备朝着高精尖方向发展,其工作环境也越来越恶劣,导致获取的信号不仅复杂多变,且信噪比极低。经典双稳态随机共振方法遭受内在饱和的限制,难以彰显随机共振的潜在增强性能。为了改善随机共振增强能力,提出了自适应分段线性非饱和双稳态随机共振方法,该方法通过线性化经典双稳态势,获得克服饱和问题的分段线性双稳态势函数,基于该势函数模型利用遗传算法自适应的优化系统参数,实现了参数之间的协同作用,从而能够实现早期故障的微弱特征增强与提取。通过仿真和轴承故障实验,表明提出的方法相比经典的随机共振方法具有更好的增强与提取能力,有益于更低信噪比环境的微弱特征增强。然而,提出的方法难以定量描述故障的发展程度,只能定性判断故障的有无,因此下一步工作将主要研究基于随机共振的定量故障诊断方法,实现故障发展程度的趋势预测。
[1]QIAO Z J,PAN Z R.SVD principle analysis and fault diagnosis for bearing based on the correlation coefficient[J].Measurement Science and Technology,2015(26):085014.
[2]SAWALHIN,RANDALLR B.Vibration response of spalled rolling element bearings:observations simulations and signal processing techniques to track the spall size[J].Mechanical Systems and Signal Processing,2011(25):846-870.
[3]THAM JY,SHENL,SENGL L,et al.A general approach for analysis and application of discrete multiwavelettransforms[J].IEEE Transaction on Signal Processing,2000(48):457-464.
[4]BENZIR,SUTERA A,VULPIANI A.The mechanism of stochastic resonance[J].Journal of Physics A:Mathematical and General,1981,14(11):453.
[5]HED.A novel wireless sensor networks multilateration positioningmethodbasedonquarticdouble-well bistablestochasticresonancetechnique[J].Nonlinear Theory and Its Applications,IEICE,2017,8(1):49-57.
[6]KOJIMA N,LAMSAL B,MATSUMOTO N.An adaptive tuningstochasticresonanceapproachforimageenhancement onillumination variant images[J].Journal of the Institute of Industrial Applications Engineers,2017,5(1):24-31.
[7]KLAMECKIBE.Use of stochastic resonance for enhancement of low-level vibration signal components[J].Mechanical Systems Signal Processing,2005(19):223-237.
[8]焦尚彬,何童.基于双稳随机共振的多频弱信号检测[J].计算机工程与应用,2014,50(5):221-226.
[9]潘峥嵘,谯自健,张宁.基于符号序列熵的自适应随机共振的微弱信号检测[J].计量学报,2015,36(5):496-500.
[10]LEI Y G,HAND,LINJ,et al.Planetary gearbox fault diagnosis using an adaptive stochastic resonance method[J].Mechanical Systems and Signal Processing,2013,38(1):113-124.
[11]LEONARDO B,MATTHEW O T C,ANDREW J H,et al.Weak signal detection based on two dimensional stochastic resonance[C]∥23rd European Signal Processing Conference,2015.
[12]QIAO Z J,LEI Y G,LIN J,et al.An adaptive unsaturated bistable stochastic resonance method and its applicationin mechanical fault diagnosis[J].Mechanical Systems and Signal Processing,2017(84):731-746.
[13]谯自健.基于随机共振理论的微弱信号检测方法研究及应用[D].兰州:兰州理工大学,2015.
[14]REBOLLEDO-HERRERA L F,FV G E.Quartic double-well system modulation for under-damped stochastic resonance tuning[J].Digital Signal Processing,2016(52):55-63.
[15]QIAO Z J,LEI Y G,LIN J,et al.Stochastic resonance subject to multiplicative and additive noise:The influenceofpotentialasymmetries[J].Physical Review E,2016,94(15):052214.
[16]SHIPM,DINGX J,HAN D Y.Study on multifrequencyweaksignaldetectionmethodbasedon stochastic resonance tuning by multiscale noise[J].Measurement,2014,47(1):540-546.
[17]ZHANG H,HE Q,LU S,et al.Stochastic resonance with a joint woods-saxon and gaussian potential for bearing fault diagnosis[J].Mathematical Problems in Engineering,2014,Article ID 315901.
(编辑:刘杨)
Study on incipient fault diagnosis of machinery based on piecewise linearity and unsaturated stochastic resonance
DUAN Jialei
(Xi’an Polytechnic University,Xi’an 710600,China)
An unsaturated stochastic resonance method based on piecewise linear bistable potentials function model is proposed aiming at the problem that fault signature of large-scale mechanical equipment is hard to be extracted in hostile operation environment.Initially,the method replaces classical bistable potentials function with piecewise bistable potentials function.Second,frequencyshifted scale transform was used to transfer the vibration signals of machinery into small parameters for satisfying the input conditions of stochastic resonance.Finally,the system parameters of unsaturated stochastic resonance were optimized by using SNR of system output signal as objective function of genetic algorithms to strengthen and extract incipient fault of mechanical equipment.Simulation analysis shows that the proposed method was able to effectively extract weak fault impact characteristics overwhelmed by strong noise background,and the bearing test proves that it can be used to strengthen and extract the fault characteristics frequency.In addition,the simulation and test results further indicate that the proposed method is superior to classical bistable potentialsstochastic resonance method and it can not only obtain higher input signal-to-noise ratio but also possess higher amplitudes at the fault characteristic frequencies of bearings.The proposed method can not only overcome the inherent output saturation problem of classical bistable potentials stochastic resonance system but also achieve moreover can achieve the optimal matching between the system and input signals based on genetic algorithm.
unsaturated stochastic resonance;fault characteristic extraction;signal-to-noise ratio;incipient fault diagnosis
A
1674-5124(2017)08-0106-07
2017-02-09;
2017-03-25
段佳雷(1987-),男,陕西富平县人,助理工程师,硕士,研究方向为基于嵌入式的信号与图像处理、机械故障诊断、助老机器人等。
10.11857/j.issn.1674-5124.2017.08.022
