上面级快速星图匹配算法研究

李超兵，李兰兰，温亚北京航天自动控制研究所，北京100859

上面级快速星图匹配算法研究

李超兵＊，李兰兰，温亚
北京航天自动控制研究所，北京100859

现有星图匹配算法存在搜索时间慢、算法实时性差的问题。为了满足上面级实时性的要求，文章采用K矢量查找算法来提高查找快速性，选择星对角矩作为星图匹配的特征量，构造星对角矩矢量，采用星棱锥星图匹配算法进行星图识别。最后采用上下位机的形式进行仿真分析，结果表明采用该星棱锥快速星图匹配算法成功率在99%以上，识别时间最长约为100ms，平均时间在15ms以内。该算法能够满足上面级对匹配算法快速性和高精度的要求。

上面级；天文导航；星对角距；星图匹配；K矢量查找算法；星棱锥算法

运载火箭上面级是航天运输系统的重要组成部分，它是在基础级火箭上面增加的相对独立的一级（或多级），上面级具有较强的任务适应性，其工作段通常已经进入了地球轨道，能够完成轨道滑行、轨道机动、有效载荷的分离与部署等任务，是提高运载火箭性能和增强任务适应能力的有效途径。目前较为先进的上面级：美国的通用半人马座，该上面级2002年首飞，真空推力达到198.4kN，采用液氢／液氧推进剂；俄罗斯的KVRB，该上面级目前正在研制，真空推力达到102.9kN，采用液氧／煤油推进剂；欧洲的ESC－A，该上面级2002年首飞，真空推力达到64.8kN，采用液氢／液氧推进剂［1－2］。先进上面级一般具有独立于运载火箭和有效载荷的制导、导航与控制系统，能够多次启动、长时间工作、自主飞行，具备多星发射和轨道机动、轨道部署的能力［3］。

由于上面级工作时间长于基础级火箭，可达30min至数天不等，上面级多采用惯性导航系统，但是惯性导航系统的误差会随时间增长，因此纯惯性导航不能满足上面级对高精度导航的要求，而天文导航是通过测量自然天体相对航天器的矢量方向来实现定位导航，具有直接、自然、可靠、精确的优点，且导航误差不随时间积累［4］，因此天文导航系统能够满足上面级对高精度的要求，天文导航的重点是星图匹配算法。

星图匹配算法主要应用于星敏感器的初始姿态捕获。星敏感器具有两种工作模式：初始姿态捕获模式和跟踪模式［5－6］。姿态捕获模式需要在没有先验信息的条件下获取载体的姿态，是星图匹配的最关键技术［7－8］。常见的星图匹配算法包括：三角形及其改进算法［9－10］、基于神经网络的星图匹配算法、基于遗传算法的星图匹配算法、基于奇异值分解的星图匹配算法

等［11－12］。

无论采用何种星图匹配算法，都不可避免地要对导航特征库进行查找，经典的对导航特征库查找算法有顺序查找和二分查找，其算法的时间复杂度分别为O（n）和O（log2n）［13］，运算量较大，实时性难以满足。为了提高查找的快速性以满足上面级实时性的要求，本文主要研究基于K矢量查找的星棱锥快速星图匹配算法。

1 快速星图匹配算法

1.1 K矢量查找算法

Mortari等人提出了K矢量查找技术［14］，本文将该查找技术运用在星图匹配算法上，可以大大提高匹配速度，节省查找时间。该查找技术的核心是构造单调的K矢量查找表，建立K矢量与导航特征量的映射关系。

设y是升序排列的长度为n的向量，y＝［ymin…ymax］T，定义ξ为一小量，过点（1，ymin－ξ）和（n，ymax＋ξ）作一条直线。该直线的方程为：

式中：m，q分别为该直线的斜率和截距：

实际上，K（i）表示向量y中小于z（i）的元素数目。

如图1所示，对10个元素构成的向量（图中×点）进行K矢量构造，图中过直线上点z（i）的小横线可以指示K矢量，即小横线之下向量y元素的个数为K矢量元素的取值：｛0，2，2，3，3，5，6，8，9，10｝。

图1 K矢量构造示例Fig.1 Example of Kvector construction

如果观测值落入的范围为［ya，yb］，则其对应的K矢量元素序号为：

式中：⌊x」表示小于x的最大整数，「x⌉表示大于x的最小整数。当jb、jt计算出来之后，则可以计算kst和ke：

对图1而言，jb＝6，jt＝9，代入式（5）可得kst＝6，ke＝9，这意味着可能的取值在向量y的序号为kst和ke，即量测值必然落入y（kst）～y（ke）。由上述分析可知，通过K矢量查找技术能够减少搜索时间，因为仅仅通过式（4）和式（5）即可确定出可能取值的上下限，这两个式子的时间复杂度均为O（1）。

1.2 星对角距的K矢量构造与查找

在星图图像中可以作为星图匹配特征信息为星点的坐标和星点的亮度，分别对应于星表中天球坐标系下导航星的坐标（赤经和赤纬）和星等。星等常被认为是一种不可靠的信息量，由于图像传感器的频谱响应特性的差异，仪器星等和视星等并不一致。此外有些恒星的星等并不是固定不变的。因此，在星图匹配中尽量少用星等信息进行判别。

实际中，常常用星间角距作为特征匹配量，因为角距不但可以通过观测星图准确计算出来，而且相对于天空中的恒星而言，相互间角距随时间改变很小，可以认为其在非常小的门限内变化。此外，角距在坐标变换中保持不变，是一种可靠的特征量。

基于上述分析，本文采用星对角距作为特征值，首先将所有导航星可能组成的星对角距的余弦值按从小到大做成数据库，显然，角距的最小值ϑmin与星敏感器CCD的测量精度有关，本文中取：

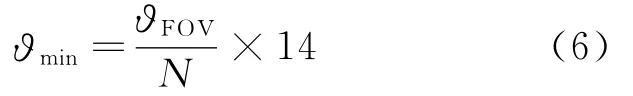
式中：ϑFOV为CCD视场角度；N＝max（Nx，Ny），Nx，Ny为CCD相机像素平面x，y轴向像素数目；14来自像素窗口大小，最大值与其视场ϑFOV相关。

假设两颗导航星在导航星库编号为i、j，两颗导航星在天球坐标系下的矢量为ri、rj，则其角距的余弦值：

定义矢量Sp为导航星对角距数据库，其每一个元素由两颗导航星编号及角距余弦值组成。Sp的元素按照星对角距余弦值升序排列。如果两颗导航星的角距余弦值满足：

则须将其信息加入到导航星对角距数据库Sp中，其中航天器星敏感器一般采用大视场，视场范围14°～20°不等。

根据第1.1节介绍的K矢量查找技术，可以连接两个端点［1，Sp（1）·cosθ］与［n，Sp（n）·cosθ］，两端点之间有n－1个间隔，可以得到平均每个元素Sp（k）所占间隔为：

过点1，Sp（1）·cosθ－D／2［

其中：按照式（3）构造K矢量。K（i）表示向量Sp中小于（a1i＋a0）的元素数目。

如果两颗导航星（p，q）在CCD上成像构成星对，其角距量测值为θ，测量误差为ε，则导航星（p，q）在建立的K矢量查找表中的位置为：

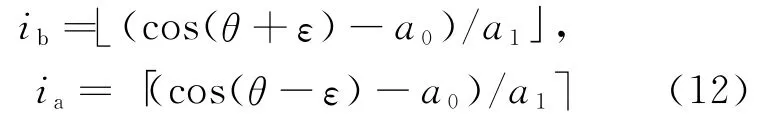
利用式（5）可求得：

式中：kst和ke为查找值在矢量Sp的索引范围，即星对角距值落在［θ－ε，θ＋ε］的可能值的集合为：

ε的选取对K矢量查找有直接影响：过小则可能查找失败，过大则查找结果过多影响后面的匹配速度，甚至匹配失败。本文采用一种工程中ε的选取方法［11］，即

式中：σs（1σ）为单星测量精度。

式中：σc为质心提取精度，亚像素的质心提取精度可取0.1像素。

由上述分析可以看出，对给定的星对角距量测值θ，测量误差ε，可以通过K矢量查找技术迅速给出CCD上成像为该角距的可能星对集合：｛Sp（kst），Sp（kst＋1），…，Sp（ke）｝为星图匹配奠定基础。

1.3 基于K矢量查找的快速星棱锥星图匹配算法

星棱锥识别算法即金字塔算法，该方法并不依赖导航星的星等信息，如图2所示为星棱锥识别算法采用的基准星结构，该星棱锥包含一个基准星三角（采用i、j、k表示），还有一颗确认星r。

图2 星棱锥Fig.2 Star pyramid

假设星图内共有n颗观测星，星棱锥识别法的算法流程如图3所示，具体步骤为：

1）如果n＜3，无法进行星图匹配；如果n＝3，不能构成星棱锥，算法退化为验证星三角形是否唯一，在这里要注意排除镜像三角形的影响。解决方法为：3颗观测星观测三角形的标号为i、j、k，相应的3颗来自导航星库的导航星构成的导航三角形标号为I、J、K，如果满足：rk）］则认为观测三角形不是镜像三角形。

2）如果n＞3，在所有星三角中选取一个匹配唯一的三角形［i，j，k］，作为基准三角形，开展步骤3）；若所有三角形均不满足要求，则星图匹配失败；此步骤中也可以使用式sgn［bTi（bj×bk）］＝sgn［rTi（rj×rk）］对镜像三角形进行剔除。

3）如果步骤2）找到了一个高置信度的基准三角形［i，j，k］，则在剩余星中找一颗参考星r验证基准三角形［i，j，k］，如果找到的r使星棱锥［i，j，k，r］匹配唯一，则转入步骤4）；否则转到步骤2），重新确定一个基准三角形。4）如果步骤3）成功地构建了星棱锥［i，j，k，r］，则这4颗星具有极高的置信度，接着就可以用其中的3颗基准星［i，j，k］对剩余的其他星p进行验证，如果能通过验证则认为星p是正常星；不能通过验证，则认为星p是假星。

星棱锥匹配算法的基本准则就是：严格根据先验信息建立高置信度的唯一匹配，宁可匹配失败也不能输出低置信度的识别结果。因为现代的姿态估计算法能够容忍数据更新率的不足，却不能忍受错误的星图匹配结果。

星棱锥匹配的基础是三角形识别，下面简要说明其原理。如图2所示，对3颗观测星［i，j，k］，其两两组成的角距分别为ϑij，ϑjk，ϑki，在角矩数据库Sp中按照式（12）、式（13）查找，可以得到3个星对集合：

图3 星棱锥匹配算法流程Fig.3 Procedure of star pyramid matching algorithm

3个集合的构成元素分别简写为Sp1、Sp2、Sp3，每个元素的组成见式（7）：即由两颗星编号num1和num2星对角距余弦值cosθnum1，num2组成，为（cosθnum1，num2，num1，num2）。三角形匹配成功的一个的条件为：

2 仿真分析

本文设计采用如图4所示的仿真结构进行星图快速匹配算法的仿真。CCD参数如表1所示。仿真下位机采用DSP6713进行星图匹配算法和定姿算法的仿真。上位机进行星图模拟仿真及定姿结果显示。星图模拟包括导航星库的建立及恒星星等的灰度模拟，星图的模拟主要是将导航星的天球坐标转换到星敏感器坐标系下，可以通过姿态矩阵实现，如图5所示。本文的星图模拟采用SAO原始星表，筛选出5等星作为导航星库。并将该导航星库作为下位机星图匹配算法的参考星库。

整个仿真过程如下：设计了一条1 800s的飞行器飞行轨迹。上位机模拟飞行过程中观测到星图的变化，每秒模拟一张星敏感器拍摄的星图，如图6所示，从星图中进行星点质心提取，并通过网络将星图质心坐标信息发送给下位机；下位机进行星图匹配和定姿运算，匹配完成后，下位机将匹配结果发送给上位机，上位机将识别时间进行存储和显示。

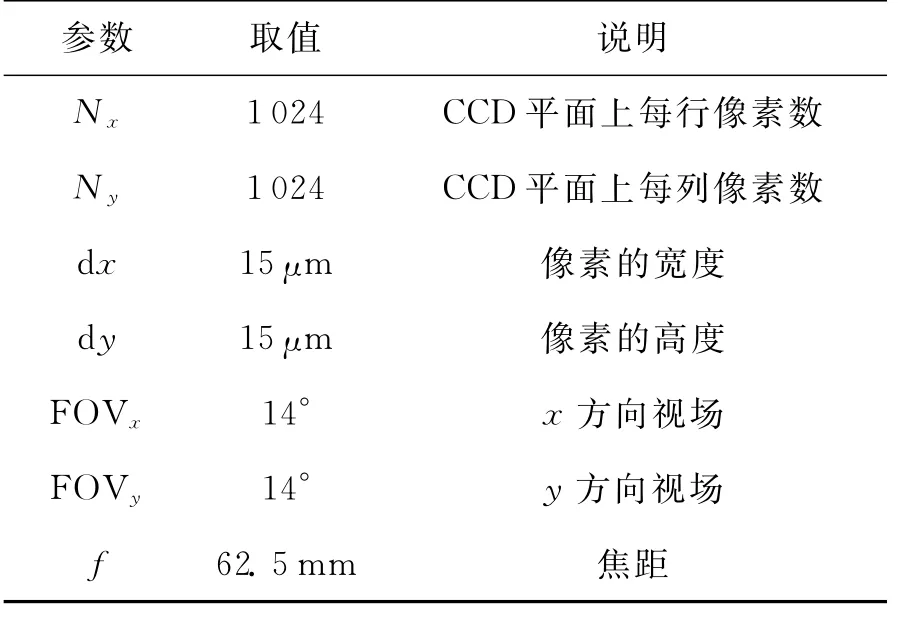
表1 星敏感器CCD光学参数取值Table 1 Optical parameters of CCD

图4 仿真系统结构框图Fig.4 Diagram of simulation system

图5 星图模拟的流程Fig.5 Procedure of star map simulation

图6 上位机模拟产生的星图（反色显示）Fig.6 Star map produced by host computer

飞行过程中共生成1 800张照片，识别成功率100%，具体结果如图7～图10所示：识别时间的均值与标准差分别为μ＝12.4ms，σ＝22ms，且识别时间在50ms以内的占95%以上。

图7 视场内观测星数概率分布Fig.7 Normal probability of star number

图8 识别时间概率分布Fig.8 Normal probability of identification time

图9 识别时间Fig.9 Identification time

图10 识别结果（0为成功，1为失败）Fig.10 Result of identification

3 结束语

本文研究了K矢量查找算法与星棱锥快速星图匹配算法，并进行仿真分析，由仿真结果可得出以下结论：本文设计的上面级快速星图匹配算法的成功率在99%以上，DSP6713运行算法时识别最大时间约为100ms，平均时间在15ms以内，能够达到上面级天文导航系统对星图匹配算法快速性和高精度的要求，为天文导航系统的工程应用奠定了基础。但是本文只考虑了视场中没有假星的情况，工程应用中情况复杂，很可能出现假星，当视场中出现假星的情况，本文中设计的上面级快速星图匹配算法是否还有如此高的速度和精度还需要进一步验证。

（

）

［1］ 马昆.上面级发展现状及趋势分析［J］.导弹与航天运载技术，2013，329（6）：24－28.MA K.Development status and trend analysis of upper stages［J］.Missiles and Space Vehicles，2013，329（6）：24－28（in Chinese）.

［2］ 林木.运载火箭上面级功能与技术发展分析［J］.上海航天，2013，178（3）：33－38.LIN M.Functional and technical progress of upper stage for launchers［J］.Aerospace Shanghai，2013，178（3）：33－38（in Chinese）.

［3］ 张利宾.火箭上面级导航、中途修正与姿态控制研究［D］.哈尔滨：哈尔滨工业大学，2010.ZHANG L B.Study on navigation，midcourse correction and attitude control of launch vehicle upper stage［D］.Harbin：Harbin institute of technology，2010（in Chinese）.

［4］ 张利宾.运载火箭上面级惯性与天文组合导航系统设计［J］.光学精密工程，2010，18（11）：2473－2481.ZHANG L B.Design of INS／CNS integrated navigation system for launch vehicle upper stage［J］.Optical Precision Engineering，2010，18（11）：2473－2481（in Chinese）.

［5］ 贾辉.高精度星敏感器星点提取与星图识别研究［D］.长沙：国防科学技术大学，2010.JIA H.Star centroid estimation and star identification of high accuracy star tracker［D］.Changsha：National University of Defense Technology，2010（in Chinese）.

［6］ 刘美莹.CCD天文观测图像的星图识别和天文定位方法研究［D］.西安：中国科学院研究生院（西安光学精密机械研究所），2010.LIU M Y.Research on CCD star map identification and celestial position［D］.Xi′an：Xi′an Institute of Optics and Precision Mechanics，Chinese Academy of Sciences，2010（in Chinese）.

［7］ GONG J Q，MA J，TIAN J W，et al.A flower algorithm for autonomous star pattern recognition［C］.47thAIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition，Aerospace Sciences Meetings，Orlando，Florida，5－8 January，2009.

［8］ CAMPBELL M E，et al.A celestial orientation system based on star pattern recognition［J］.Journal of Spacecraft and Rockets，2009，2（6）：962－963.

［9］ PALADUGU L.Intelligent star pattern recognition for attitude determination：the"Lost in Space"problem［J］.Journal of Aerospace Computing，Information，and Communication，2009，3（11）：538－549.

［10］ COLE C L，J L CRASSIDIS，et al.Fast star－pattern recognition using planar triangles［J］.Journal of Guidance，Control，and Dynamics，2009，29（1）：64－71.

［11］ 张力军.基于多视场星敏感器的航天器姿态确定方法研究［D］.长沙：国防科学技术大学，2011.ZHANG L J.Spacecraft attitude determination for multiple fields of view star sensors［D］.Changsha：National University of Defense Technology，2011（in Chinese）.

［12］ 邢飞，尤政，董瑛，等.基于导航星域和K矢量的快速星图识别算法［J］.宇航学报，2010，31（10）：2302－2308.XING F，YOU Z，DONG Y，et al.A rapid star identification algorithm based－on navigation star domain and K－vector［J］.Journal of Astronautics，2010，31（10）：2302－2308（in Chinese）.

［13］ THOMAS H CORMEN，CHARLSE E LEISERON，RONALD L.Introduction to algorithm［M］.Rivest and Clifford Stein：The MIT Press，2001.

［14］ MORTARI D，NETA B.K－vector range searching techniques［C］∥The 10th Annual AIAA／AAS Space Flights Mechanics Meeting，Paper AAS 00－128，Clearwaters，FL.，23－26Jan.，2000.

（编辑：车晓玲）

Research on quick star identification algorithm of upper stage

LI Chaobing＊，LI Lanlan，WEN Ya
Beijing Aerospace Automatic Control Institute，Beijing 100859，China

Present star identification algorithms have the problem of real－time calculation.In order to meet the navigation requirement of the upper stage，the Kvector search algorithm was employed，the inter－star angles as the matching feature quantity were selected and the star pyramid matching algorithm was used.Finally，simulation results indicate that the success rate of this algorithm is more than 99%，the maximum time of identification is about 100ms，and the average time is less than 15ms.The algorithm can meet the matching speed and precision requirements of the upper stage.

upper stage；celestial navigation；inter－star angles；star identification；Kvector search algorithm；pyramid algorithm

V249.32＋3

A

10.16708／j.cnki.1000－758X.2017.0053

2016－11－23；

2017－05－08；录用日期：2017－06－29；网络出版时间：2017－08－11 10：47：51

http：∥kns.cnki.net／kcms／detail／11.1859.V.20170811.1047.007.html

＊通讯作者：李超兵（1981－），男，硕士，高级工程师，lcbpku＠163.com，研究方向为航天器导航制导与控制

李超兵，李兰兰，温亚.上面级快速星图匹配算法研究［J］.中国空间科学技术，2017，37（4）：56－62.

LI C B，LI L L，WEN Y.Research on quick star identification algorithm of upper stage［J］.Chinese Space Science and Technology，2017，37（4）：56－62（in Chinese）.