基于LDQPSO算法的非刚体配准

颜翠翠++王浩军++袁观娜

DOI：10.16661/j.cnki.1672-3791.2017.22.236

摘 要：如何快速准确地实现匹配一直是非刚体配准领域极具挑战性的问题。针对该问题，该文提出一种快速、高精度的非刚体配准方法——基于LDQPSO的非刚体配准算法。首先针对QPSO算法过早收敛的缺点，采用线性自适应策略对QPSO惯性权重因子进行更新，提出了LDQPSO算法。在此基础上，用LDQPSO实现非刚体点云配准参数的优化确定，最终实现了快速高精度的非刚体点云配准。文中选择不同的非刚体配准实例验证算法有效性，并与原有算法进行对比。实验表明该文提出的算法具有更好的尋优性能。

关键词：非刚体 LDQPSO 优化

中图分类号：TN91 文献标识码：A 文章编号：1672-3791（2017）08（a）-0236-04

基于点的特征匹配问题一直是计算机视觉、模式识别等领域中一个基础而重要的课题。在实际应用中，如目标跟踪，常常需要对存在非刚性形变的场合进行快速精确的配准，进而实现高效的目标跟踪，因此，如何实现准确快速的配准尤其是非刚体配准显得尤为重要。

2003年，Chui等[1]提出的基于TPS构造能量函数，用于非刚体点云配准中，然而该算法是基于SA算法实现的，实际求解对于多峰函数寻优具有局限性。PSO算法需控制的参数少，易实现且对多峰函数寻优具有很好的效果。2004年，冯林[2]提出基于PSO算法的点匹配方法。但标准PSO算法并不能以绝对概率寻得全局最优，故文献[2]算法易陷入局部最优。

一个好的优化算法，必须能够很好地平衡算法的“开发能力”和“探索能力”。种群多样性是衡量算法“开发能力”和“探索能力”的重要依据。2011年，Shi等[3]给出了多样性的定义，并指出量子粒子群优化算法本质上是一种PSO多样性控制的算法。因此，多样性控制研究中，对量子粒子群优化算法进行研究，具有实际的价值和意义。基于此，该文对QPSO算法的惯性权重系数采用线性+自适应的策略进行更新，提出了LDQPSO算法（Linear adaptive QPSO），有效地解决了标准PSO算法过早收敛到局部最优的问题。并进一步将LDQPSO应用于非刚体配准的一一对应关系和映射函数参数的优化中，有效地提高了非刚体点云配准问题的精确性性和快速性。

1 非线性自适应QPSO算法原理

该节首先简要介绍标准QPSO的基本原理，接着详细介绍该文所提出的LDQPSO算法原理及实现步骤。

1.1 标准QPSO算法原理简介

2004年，Sun[6]从量子力学的角度提出了QPSO算法，粒子的位置方程为：

（1）

其中，u为在[0，1]之间的随机数，L由式（2）确定：

·β· （2）

最后，得到QPSO算法的进化方程为：

（3）

（4）

其中，D表示粒子的维数，表示所有粒子的平均最优值，N表示粒子数目，u是在[0， 1]均匀分布的随机数。第i个粒子的最优。β是算法收敛的重要且唯一参数。

1.2 LDQPSO算法原理

参数对于算法寻优性能至关重要，如何选择最优策略确定最佳参数促进算法寻优性能是相当复杂的问题。受SA启发，分析式（3）容易发现，β较大时算法以较快速度在全局寻优，但此时的解往往不是最精确的；β较小时算法以较慢速度在局部寻优，此时更易寻得全局最优解。因此，可设置随着迭代进行β在一定范围内逐步递减，最终搜索到最优解。

该文提出的LDQPSO算法基本思想为：初期为粗匹配，对β控制采用式（6）策略，此时β值较大，算法收敛速度较快，侧重于促进算法在全局搜索所有的解，粒子之间进行信息交互，向当β前全局最优解“聚拢”；当达到预设值时算法进入精匹配，对β控制采用式（7）策略，算法寻优速度较初始有所降低，粒子集中在局部搜索更精准的最优值。

β=f （a，e）=β-s·β01+a·β02 （6）

（7）

其中，β0和β1分别为β的最大、最小值；t表示算法当前的迭代次数；表示算法的最大迭代次数；s为进化速度因子，s的取值范围为0

（8）

（9）

上式中，表示当前迭代的全局最优，表示上一次迭代的全局最优，表示当前迭代所有粒子最优的均值，见式（10）：

（10）

综上所述，基于式（6）、式（7）所示策略，改进算法在初期寻优过程中，探索能力增强，有效促进了算法的全局搜索能力；在末期寻优过程中，开发能力增强，使得算法能够更有效的寻得全局最优解，进而平衡算法探索能力和开发能力。

2 基于NLAPSO算法的非刚体配准原理

该部分首先简要介绍非刚体点云配准，接着对该文所提出的基于LDQPSO算法的非刚体点云配准算法原理及流程进行介绍。

2.1 基于TPS的非刚体配准

基于TPS的非刚体配准思想是：在确定点集之间对应关系后，通过最小化TPS函数，嵌入合适的优化算法框架中，对空间映射函数f和对应矩阵H进行交替求解，最终确定最优的f和H值，进而实现点云配准。基于TPS的非刚体配准算法的函数表示如下：

（11）

选择适当的优化算法对应矩阵H和映射函数f （c，d）进行求解，进而即可实现非刚体配准。

2.2 基于LDQPSO的非刚体配准原理

基于LDQPSO的非刚体配准算法原理为：将式（11）目标函数的最优化求解嵌入到LDQPSO算法中，求解参数值。基于LDQPSO算法的非刚体配准算法流程见图1。

此处，和初值分别设置为。

3 仿真研究

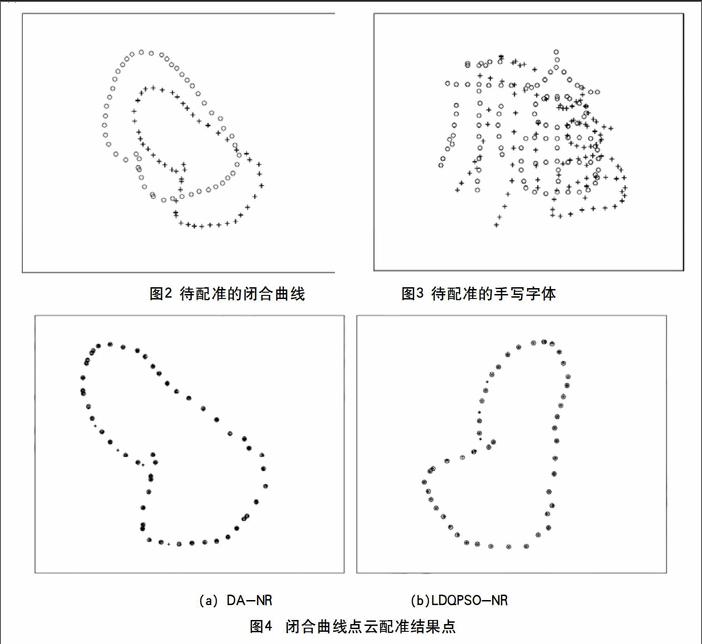
该节共选择两组典型点云数据进行非刚体配准仿真，验证该文算法的有效性。仿真图中模板点集均为圆圈，目标点集均为十字。图2中模板点集为闭合曲线，而待匹配的目标点集是一组与模板点集相似但在底部存在形变的闭合曲线；图3中模板点集和目标点集均为手写“福”字的點云，两组数据看起来相似，但实际存在较大非刚体形变。分别采用基于SA的非刚体配准算法（DA-NR）[1]和该文提出的基于LDQPSO的非刚体配准算法（LDQPSO-NR）对这些数据进行配准，分别采用主观和客观两种评价方式进行性能评价。

3.1 主观评价

（1）闭合曲线点云仿真实例。

图4（a）为DA-NR配准结果，图4（b）为该文提出LDQPSO-NR配准结果。配准结果表明LDQPSO-NR在DA-NR不能很好实现配准的位置也取得了较好的匹配结果。

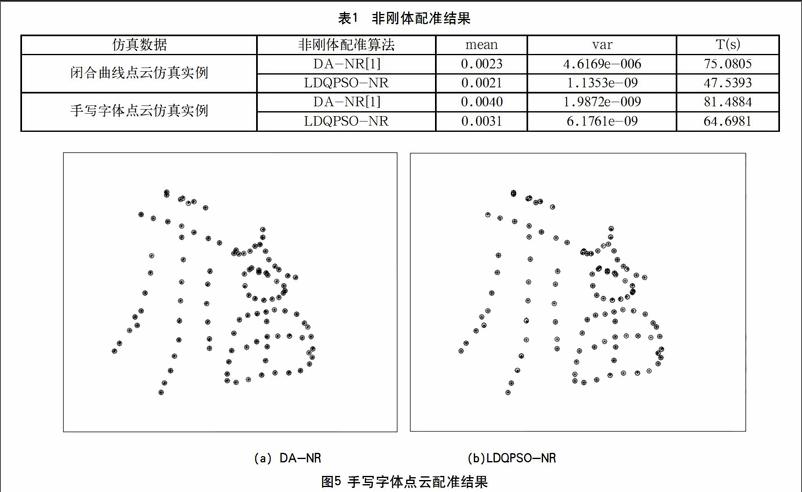
（2）手写字体点云仿真实例。

图5（a）为DA-NR配准结果，图5（b）为该文提出LDQPSO-NR配准结果。结果表明，本文算法和DA-NR均取得了精准的配准结果。

3.2 客观评价

表1中列出了DA-NR[1]和该文LDQPSO-NR下，经过30次测试得到的式（11）函数最优值均值和方差，分别用mean和var表示最优值均值和方差，T表示达到配准时所需时间。

由表1可知，LDQPSO-NR算法求得的函数均值、方差均优于DA-NR算法，该数据验证了该文算法的高精度和高稳定性。此外，从程序运行时间上看，该文算法明显优于DA-NR算法，验证了该文算法的快速性。

4 结语

该文提出了一种LDQPSO非刚体配准算法。通过对QPSO参数改进，迭代初期粒子在全局范围内进行粗寻优，侧重于提高算法收敛速度；随着迭代次数增加，粒子趋向于精寻优，侧重于提高算法精度。实验部分选择两组典型非刚体点云数据对基于该文算法的配准结果和基于SA算法的配准结果进行对比，由结果可知，该文算法在精确性、稳定性和快速性方面均表现出更好的配准结果。下一步工作可将该文算法用于一些实时配准问题中。

参考文献

[1] Chui Haili， Rnagarajna A. A new point matching algorithm for non-rigid registration[J].Computer Visionand Image Understanding，2003，89（2-3）：114-141.

[2] 冯林，张名举.基于粒子群优化技术的点匹配算法[J].系统仿真学报，2004，8（16）：193-194.

[3] Shi Cheng and Yuhui Shi.Diversity control in particle swarm optimization. In Proceedings of 2011 IEEE Symposium on Swarm Intelligence （SIS 2011）[M].Paris，France，2011：110-118.

[4] 郑立华，麦春艳，廖崴，等.基于Kinect相机的苹果树三维点云配准[J].农业机械学报，2016（5）：134-135.endprint