正/负频率和频率响应概念的三维揭示

吴宪祥, 郭宝龙, 闫允一, 朱娟娟, 孟繁杰

(西安电子科技大学 空间科学与技术学院， 陕西 西安 710071)

正/负频率和频率响应概念的三维揭示

吴宪祥, 郭宝龙, 闫允一, 朱娟娟, 孟繁杰

(西安电子科技大学 空间科学与技术学院， 陕西 西安 710071)

频谱是“信号与系统”教学中的一个重点和难点。其中，“负频率”的概念非常抽象和难以理解。本文借助Matlab工具对正、负频率分量的物理意义在三维空间进行揭示，并讨论频率响应函数的物理内涵，以此加深学生对频谱概念和频域分析的理解，以期取得更好的教学效果。

信号与系统; 正/负频率; 频率响应; Matlab

0 引言

在“信号与系统”课程教学中，借助Matlab工具辅助进行教学已成为国内、外广大任课教师的共识[1]。

周期信号指数形式傅里叶级数展开或者一般信号傅里叶变换得到的频谱为复数，频率范围从-∞～∞，所以称为双边谱。由于频谱概念比较抽象，学生在学习相关概念时容易混淆。一些教材中论述“双边谱中负频率只有数学意义，没有物理意义”，这段叙述应当如何理解，学生会有些迷惑[2-4]。本文将借助Matlab工具绘图，进一步对负频率和频谱的概念进行揭示和探讨。

1 频率与负频率

频率是什么？频率被定义为“物质在1s内完成周期性变化的次数”。从定义来看它是一个标量，这便造成人们对负频率产生疑问的原因之一。回顾电路相量法分析，ejω被称为旋转因子，是模值等于1，初相为零，并以角速度ω逆时针旋转的复函数。单位圆上的点，逆时针旋转为正频率，那顺时针旋转就是负频率，不旋转为0。可见，频谱中引入复数概念之后，负频率是有明确物理意义的。

2 正负频率分量物理意义揭示

根据傅里叶变换的定义：

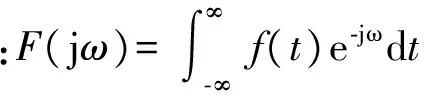
(1)

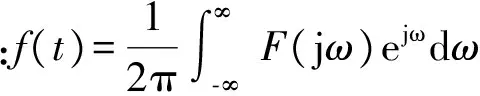
(2)

傅里叶变换可理解为将一个信号分解为无数个ejω分量之和。如前所述，正频率可视为旋转因子逆时针旋转，负频率可视为旋转因子顺时针旋转，如图1(a)和图1(b)的正视图所示。若将这一关系表示在一个由复平面和与之垂直的时间轴构成的三维空间，便可以更好地揭示负频率的物理意义[5]。ejω在复平面和时间轴构成的三维空间中呈现为类似于弹簧的螺旋线形状。对于正频率和负频率，螺旋的方向相反，如图1所示。

(a) 正频率

(b) 负频率图1 复指数函数ejω0t的三维图像

螺旋线在时间轴和实轴构成的平面上的投影见图1俯视图。其中，Real Axis表示复指数函数ejω0t实部的幅值，Time表示时间。对于正频率和负频率，尽管螺旋方向相反，但是其在实轴和时间轴构成的平面上的投影完全相同。

螺旋线在时间轴与虚轴构成的平面上的投影见图1左视图。其中，Imaginary Axis表示复指数函数ejω0t虚部的幅值，Time表示时间。对于正频率和负频率，螺旋方向相反，其在虚轴和时间轴构成的平面上的投影差了一个负号。

如果将图1中的两根螺旋线合成，由于在虚轴上的投影相差一个负号，故虚部抵消为0，合成图仅剩实部，只不过实部为原来的两倍，也就是一个余弦函数2cos(ω0t)。这点可由欧拉公式得到：

(3)

傅里叶变换用无数个复指数函数ejωt合成现实中的实信号，而复指数函数ejωt是复平面和与之垂直的时间轴构成的三维空间中的螺旋线。如果没有负频率成分，无法用复指数函数ejωt合成一个实信号。图2给出了复频率域余弦函数和正弦函数的频谱。

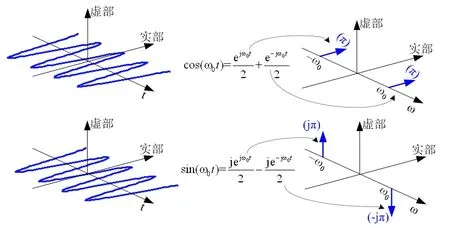
图2 复频率域余弦函数和正弦函数的频谱

其实，任何实周期信号必然由共轭的(幅度偶对称、相位奇对称)正、负频率分量组成。而这一概念在电气领域中的二相异步电机设计、通信领域中的频分复用、机械工程领域中的任意平面轨迹产生中的应用，都进一步表明了频谱中负频率的物理意义和重要性[6]。

3 频率响应函数物理意义揭示

设LTIC系统的冲激响应为h(t)，当激励是角频率ω的基本信号ejωt时，其响应

(4)

定义：h(t)的傅里叶变换，记为H(jω)，常称为系统的频率响应函数。

(5)

基本信号ejωt作用于LTIC系统的响应为

y(t)=H(jω)·ejωt=|H(jω)|∠θ(ω)·ejωt

(6)

图3是借助Matlab绘图工具，给出的基本信号ejωt作用于LTIC系统的响应H(jω)·ejωt的三维图像。对比图1(a)，H(jω)反映了系统对某一频率分量ejωt振幅和相位的响应。

(吴宪祥等文)

3 结语

在实平面研究复数问题存在一定的局限性，这直接导致了学生对频谱中负频率成分物理意义的理解存在困难。本文借助Matlab工具，从三维空间直

观地揭示了正频率和负频率的物理意义，进一步从三维空间揭示了频率响应函数的物理内涵，对于频谱概念和频域分析的教学具有良好的参考价值。

[1] 郑君里，谷源涛. 信号与系统课程历史变革与进展[J]. 南京: 电气电子教学学报, 2012,34(2): 1-6.

[2] 陈怀琛, 方海燕. 论频谱中负频率成分的物理意义[J]. 南京: 电气电子教学学报, 2008, 30(1): 29-31.

[3] 张朝阳. 关于负频率的探讨[J]. 永州: 湖南科技学院学报, 2009, 30(4): 79-81.[4] http://blog.csdn.net/wolinxuebin/article/details/7526956 [EB/OL][5] http://blog.sina.com.cn/s/blog_c159ce3f0101ab6k.html [EB/OL]

[6] 张华容,柏子游. 极形轨迹发生器[J]. 西安: 机械科学与技术, 2001, 20(4): 505-506.

3D Reveal of Positive/Negative Frequency and Frequency Response Concepts

WU Xian-xiang, GUO Bao-long, YAN Yun-yi, ZHU Juan-juan, MENG Fan-jie

(SchoolofAerospaceScienceandTechnology,XidianUniversity,Xi′an710071,China)

Frequency spectrum is one of the emphasis and difficulty in the course of Signals and Systems. Moreover, the concept of negative frequency is abstract and hard for understanding. This paper employs Matlab software to demonstrate the physics meaning of positive/negative frequency in 3D space and discusses the deeper physical intension of the frequency response function, which can effectively improve the understanding of the concepts of frequency spectrum and frequency analysis , expecting to get better teaching & learning effect.

signals and systems; positive/negative frequency; frequency response; Matlab

2016-07-15;

2017-0- 17

西安电子科技大学新实验开发项目(项目编号： SY1581)；西安电子科技大学研究生教育综合改革试点项目(项目编号：15Y2)。

吴宪祥(1980-)，男，博士，副教授，主要从事电路、信号与系统、自动控制原理、模式识别原理等方面的教学与科研工作，Email: wuxianxiang@163.com

TN911 G642

A

1008-0686(2017)03-0052-03