五轴联动磁流变抛光中双摆轴角度计算*

郑永成，黄 文，陈 华，唐小会，张云飞

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

五轴联动磁流变抛光中双摆轴角度计算*

郑永成，黄 文，陈 华，唐小会，张云飞

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

在光栅线轨迹模式下，曲面工件的磁流变抛光需通过五轴联动来实现，基于自研的PKC-600Q磁流变抛光机床运动轴配置的几何模型，给出了由曲面解析式得到的被加工点的方向余弦，并详细推导两个摆动轴角度的计算方法。该方法易于理解，不依赖CAD/CAM 软件，便于集成到磁流变抛光专用工艺软件中，同时也可以在曲面工件其他方法加工中参考应用。

曲面；磁流变抛光；光栅线轨迹；五轴联动；角度计算

0 引言

曲面光学元件，尤其是非球曲面具有良好的光学性能，它可以消除球面镜片在光传递过程中产生的多种像差，减少光能损失，从而改善光学系统成像质量，提高光学性能，同时还可缩短工作距离，大幅度地减少镜片数量等，从而简化光路结构，实现小型化和轻量化。因此，各种曲面光学元件在军用和民用光电领域中得到了广泛的应用。然而曲面光学元件的传统制造工艺复杂，制造难度大，无法满足现代光学应用对元件制造精度近乎极限的要求。磁流变抛光技术以其稳定的去除函数，宽广的适应范围和很高的表面及亚表面质量为现代光学制造带来革命性的发展[1-3]。磁流变抛光加工是一种基于去除函数传递机制的子孔径扫掠抛光[4]，常用的轨迹模式有回转轨迹和光栅线轨迹两种。光栅线轨迹模式灵活性高，应用范围广，尤其适用于各种形状工件的非回转对称的曲面或自由曲面[5]。下面讨论基于曲面的方向余弦来计算，曲面磁流变抛光法向加工时两个摆动轴角度的计算。

1 光栅轨迹模式与曲面的方向余弦

为维持去除函数在加工过程中的确定性，磁流变抛光需满足法向等间隙加工的工艺要求。为此曲面工件的磁流变抛光需要用到X、Y、Z三个直线轴和A、B两个摆动轴共同联动来实现。曲面工件光栅轨迹磁流变抛光如图1所示。在轨迹点坐标计算时，两个摆动轴角度计算是关键，直线轴的运动相对简单。

图1 曲面工件光栅轨迹磁流变抛光

在实际加工时，被加工面是已知的，通常由解析式或矩阵表达，下面详细推导由解析式给出的曲面五轴联动磁流变抛光时两个摆动轴角度的计算方法。直线轴偏移可根据摆动轴角度与机床结构参数计算得到，这里不作讨论。

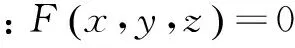
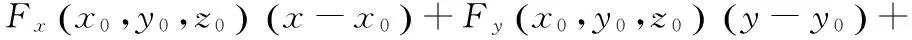
过曲面Σ上的M0点且与切平面垂直的直线称为曲面在该点的法线，其方程为：

设：

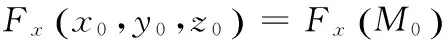
则曲面Σ在M0点法线的方向余弦为：

其中分母根号前的正负号依法线正向的选择而定，或同取正号，或同取负号。

2 几何模型与角度计算

对于自研的PKC-600Q双摆动抛光头磁流变抛光机床，其运动轴配置简化模型如图2所示。设此时A、B轴处于零位，抛光点O位于曲面一个极值点上，N0为A、B轴线公垂线上的点。如图3所示，当抛光曲面Σ上点M0处时，抛光工艺需此时的等效抛光工具原始位置矢量(即零位矢量)ON0移动到目标位置矢量M0N，矢量M0N在过M0点的曲面Σ的法线上。设M0N为1个长度单位，则在以M0为原点的坐标系中，N点的坐标值为：(X，Y，Z)=(cosα，cosβ，cosγ)。在图中延长AB到N′使AN’=AN。

由于ON0∥M0N，在只考虑摆动的条件下，抛光工具由零位矢量ON0移动到目标矢量M0N的过程等效于平行于零位矢量ON0的矢量M0Z先通过B轴摆动(即绕M0Y旋转)到M0N′，AN′再通过A轴摆动(即绕M0X旋转)到AN，此时M0N′即旋转到M0N。

图2 PKC-600Q机床运动轴配置

图3 曲面上任意M0点法向

由此便可得抛光M0点时两摆动轴的角度分量分别为：A轴角度分量θ为：

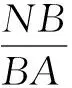
B轴角度分量φ为：

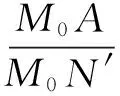
对于由矩阵形式给出的曲面，通过数值计算得到加工点的方向余弦后，也可以通过上式计算出摆动轴的角度。

3 结束语

由曲面工件磁流变抛光时等间隙法向加工的工艺需求出发，以自研的PKC-600Q磁流变抛光机床几何模型为对象，通过已知的曲面解析表达式，通过被加工点的方向余弦，提出了曲面五轴联动加工时两个摆动轴角度的计算方法，该方法物理意义明确，几何模型简单，计算简便，完全由解析计算得到，因此不引入计算误差，不依赖商业CAD/CAM软件，便于集成到磁流变抛光专用工艺软件中。在对曲面工件的其它抛光方法或机械加工中，轨迹计算中摆动轴的角度计算同样也可以用上述方法求解。

[1] 单翠云. 非球面光学曲面柔顺研抛伺服平台的研制及其试验研究[D].长春:吉林大学,2014.

[2] 张彦超，付秀华，贾宗合，等. 非球面制造中的加工误差修正补偿[J].长春理工大学学报(自然科学版)，2015，38(1)：13-16，20.

[3] 殷龙海. 大中型SiC非球面反射镜确定性高效加工工艺的研究[D].北京:中国科学院大学,2015.

[4] 郑永成，黄文，张云飞，等. 回转对称非球面磁流变加工几何模型与轨迹计算[J]. 制造技术与机床，2015(12)：60-62.

[5] 李龙响，郑立功，邓伟杰，等. 应用四轴联动磁流变机床加工曲面[J]. 光学精密工程，2015，23(10)：2819-2826.

[6] 蔡高厅，叶宗泽. 高等数学(下册)[M]. 天津：天津大学出版社，1994.

(编辑 李秀敏)

Swing-angle Calculating in 5-Axis Magneto-Rheological Finishing

ZHENG Yong-cheng，HUANG Wen，CHEN Hua, TANG Xiao-hui, ZHANG Yun-fei

(Institute of Mechanical Manufacturing Technique，China Academy of Engineering Physics，Mianyang Sichuan 621900，China)

Processing a curved surface in magneto-rheological finishing (MRF) by raster path, 5-axis machine is necessary. Based on the geometric model of axis distribution in developed PKC-600Q MRF machine, the direction cosine of the finishing point are calculated from the surface expressing, and farther on, with a simple and specific method independent of CAD/CAM software, angles of the two swing axis are also calculated from the direction cosine. The method is easy to integrate in self-developed MRF software. Besides MRF，the method is also suitable for other processing of curved surface.

curved surface; MRF; raster path; 5-axis; angle calculating

1001-2265(2017)08-0112-02

10.13462/j.cnki.mmtamt.2017.08.028

2016-09-07；

2016-11-24

国家科技重大专项：高档数控机床与基础制造装备(2013ZX04006011)

郑永成(1980—)，男，山西右玉人，中国工程物理研究院机械制造工艺研究所工程师，硕士，研究方向为超精密加工机理与装备，(E-mail)inflator@126.com。

TH166;TG506

A