基于多重自相关与包络谱分析的滚动轴承故障诊断方法研究*

张 良，杨 涛

(1.绵阳师范学院 机电工程学院，四川 绵阳 621000；2.西南科技大学 信息工程学院，四川 绵阳 621010)

基于多重自相关与包络谱分析的滚动轴承故障诊断方法研究*

张 良1，杨 涛2

(1.绵阳师范学院 机电工程学院，四川 绵阳 621000；2.西南科技大学 信息工程学院，四川 绵阳 621010)

滚动轴承在故障状态运行时，传感器测得的振动信号为非平稳、多分量的调制信号。在故障出现早期，由于调制信号微弱且含有噪声，导致故障特征难以识别，采用多重自相关消除噪声干扰，提取信号中的周期调制成分，然后利用Hilbert 变换的包络解调方法获取故障特征频率，从而判断出轴承故障类型。实验结果表明，采用多重自相关与包络谱解调相结合的方法，能较准确的提取滚动轴承故障特征频率，具有一定的工程应用价值。

滚动轴承；多重自相关；Hilbert变换；故障诊断

0 引言

据统计，由于轴承导致的故障在旋转机械所有故障中占到 1/3 左右[1]，因此对重要轴承进行工况监视与故障诊断，不但可以减少或杜绝事故发生，而且还能最大限度地发挥轴承工作潜力，这在提高生产效益以及保障生产安全方面都具有十分重要的意义[2]。滚动轴承出现局部损伤性故障的特点是微弱的周期信号宽带冲击会激起系统结构自身的高频振动[3]，同时滚动轴承振动信号的频率范围较宽，信噪比通常较低，局部损伤性所引起的冲击比较微弱，直接对振动信号解调时调制信息容易淹没在噪声中[4]，因此如何从微弱的故障振动信号中提取冲击所激起的高频振动信息进行解调分析是轴承故障诊断的关键[5]。目前，用于在低信噪比的条件下提取滚动轴承振动信号包络谱的主要方法有形态分量分析[5-6]、时延相关解调[7]、小波降噪[8-9]、局部均值分解[10-11]、经验模态分解[12-13]、盲源分离[14-15]等，上述方法在故障振动信号的包络谱解调与提取方面均有一定的效果。本文提出一种基于多重自相关的包络谱滚动轴承故障诊断方法，对原始振动信号首先进行多重自相关运算，最大限度地消除信号中混有的高斯噪声，然后在对多重自相关运算结果做带通滤波，将滤波截取的高频共振频段进行希尔伯特变换，得到包络谱，从而提取滚动轴承的故障特征频率，完成了对滚动轴承的故障诊断，通过实例分析验证了该方法的有效性。

1 理论基础

1.1 滚动轴承的频率特征

滚动轴承常见的故障形式有表面损伤、疲劳剥落、过热烧伤、电化学腐蚀、胶合及破损等[16]。可将轴承元件的这些故障归结为3种形式:内圈故障、外圈故障以及滚动体故障。当轴承元件(内圈、外圈、滚动体)出现了局部故障时，在转动过程中会与其它相接触的元件发生反复碰撞，从而产生冲击振动。这种短时周期性的低频脉冲信号频率通常称为滚动轴承的通过频率，即故障特征频率[17]。

理想情况下，滚动轴承外圈固定，内圈随转轴旋转，滚动体与滚道之间没有相对滑动，且轴向、径向在承受载荷各部件无变形时，由轴承的结构几何参数可计算出各轴承元件的理论故障特征频率[18]，其计算表达式如下：

内圈故障特征频率fi为：

(1)

外圈故障特征频率fo为：

(2)

滚动体故障特征频率foc为：

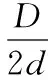
(3)

保持架故障特征频率fc：

(4)

上式中各个参数含义:D为轴承节径;d为滚动体直径;α为轴承接触角;z为滚动体个数;N为轴承转速。

而在实际的故障诊断中，由于各种干扰因素的影响，虽然理论故障特征频率值与工程诊断分析得到的检测值有一定的偏差[19]，但故障特征频率的提取与分析仍然是判断轴承故障十分重要和有效的理论依据。

1.2 多重自相关

定义rxy(τ)为信号x(t)和y(t)的互相关函数，其中τ为延迟时间。

(5)

如果设y(t)=x(t)，则上面定义的互相关函数rxy(τ)变为自相关函数rxx(t)：

(6)

rxx(t)反应了信号x(t)和自身做了一段延迟时间之后x(t+τ)的相似程度[20]。设信号x(t)=s(t)+n(t)，其中s(t)为周期信号，n(t)为高斯白噪声，将x(t)代入式(6)做自相关运算得：

(7)

将式(7)展开后得到：

rxx(τ)=rss(τ)+rsn(τ)+rnn(τ)

(8)

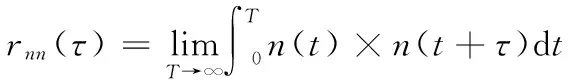
由相关函数性质[20]可知，周期信号经过自相关运算后，rss(τ)周期性与原来的周期性函数s(t)一致，但周期信号与噪声信号的互相关函数rsn(τ)，噪声信号的自相关函数rnn(τ)均趋近于0。因此利用以上结论，当含有高斯噪声的信号经过自相关运算后，可以对信号进行去噪和提取周期成分。

理论上，当测量时间T为无穷大时，rsn(τ)、rnn(τ)将趋于0，但在实际工程中，T不可能取到无穷大，所以rsn(τ)、rnn(τ)不等于0，去噪情况不会太理想。采用以下步骤进行多次自相关运算，可以减少高斯噪声，提高信噪比。

(1)设

xi(t)=si(t)+ni(t)

(9)

其中，

si(t)=rss(i)(τ)，ni(t) =rsn (i)(τ) +rnn (i)(τ)

(2)把式(9)带入式(6)做自相关；

(3)重复i次步骤(1)和步骤(2)。

这里把周期信号的自相关函数rss(τ)i看作新的周期信号，而噪声和周期信号的互相关函数rsn(τ)i、噪声的自相关函数rnn(τ)i看作新的噪声信号，i为自相关次数。对信号xi(t)做多次自相关可以有效的提高信噪比，从而更好的检测出淹没在高斯噪声中的微弱的周期信号[21-22]。

1.3 包络谱分析

采用Hilbert 变换实现对振动信号进行包络解调，进而进行频谱分析是滚动轴承故障诊断常用的方法[23-24]。

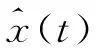
(10)

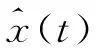
(11)

z(t)为信号x(t)的解析信号。如果x(t)受到振幅调制，则：

(12)

(13)

A(f)为振幅调制信号x(t)的包络谱。通过对滚动轴承振动信号进行上述包络谱的分析，可以提取滚动轴承的故障特征频率。

2 实例分析

为验证基于多重自相关的包络谱分析方法在滚动轴承故障诊断中的有效性，实例数据来源于美国西储大学在图1所示的实验平台上得到故障轴承数据库。从该数据库中选取电机驱动端 SKF深沟球轴承故障数据，其采样频率为12kHZ、电机负载2HP、电机转速1750r/min、故障直径0.007英寸。驱动端 SKF轴承尺寸信息如表1所示。

表1 驱动端轴承参数

根据驱动端轴承的结构几何参数可计算出各轴承元件的理论故障特征频率为表2所示。

表2 驱动端轴承各部件故障频率

图1 美国西储大学故障诊断实验平台

本文以外圈与内圈故障为例，通过表2可得内圈故障特征频率为157.5Hz，外圈故障特征频率为105Hz。图2是滚动轴承内圈和外圈发故障时的时频图。

图2 振动信号时频图

从图2可以看出原始信号时域波形复杂，频谱成分丰富，故障特征频率在频谱图中没有突出显示，已淹没在噪声中。利用1重自相关和3重自相关分别对原始信号进行滤波，结果如图 3和图4所示。

图3 1重自相关去噪后的时频图

图4 3重自相关去噪后的时频图

对比图3和图4的频谱图可明显看出3重自相关在去除高斯噪声的效果优于1重自相关，且滤波后的信号在2.5～4.5kHz频段有明显的共振峰，对该频段进行包络谱分析，其包络谱如图5所示。

图5 包络谱

从图5内圈包络谱中可以明显的看到156.7Hz、314.9Hz、629.9Hz、786.6Hz、1417Hz 5个谱峰；该频率值和和内圈故障的特征频率值157.5Hz及其2倍频315Hz、4倍频630Hz、5倍频787.5Hz、9倍频1417.5Hz值非常接近；同样在图5的外圈包络谱中也可以明显的看到105.5Hz、314.9Hz、524.4Hz、629.9Hz 4个谱峰，该频率值和和外圈故障的特征频率105HZ及其3倍频315Hz、5倍频525Hz、6倍频630Hz值非常接近，从而可以诊断出滚动轴承出现了内圈和外圈故障。

3 结论

本文将多重自相关与包络谱分析应用于滚动轴承故障诊断中。针对滚动轴承的故障特征信号容易被噪声淹没这一特点，通过对振动信号取多重自相关，减小高斯噪声对有用信号的干扰提高了信噪比；对多重自相关后得到的降噪信号进行Hilbert 变换实现了包络解调，从而较准确提取了滚动轴承的故障特征频率，完成对滚动轴承的故障检测，验证了该方法在滚动轴承故障诊断中的有效性，具有较好的工程应用价值。

[1] 韩捷,张瑞林.旋转机械故障机理及诊断技术[M].北京:机械工业出版社,1997.

[2] 陈长征,胡立新,周勃,等.设备振动分析与故障诊断技术[M].北京:科学出版社,2007.

[3] 王晶,陈果,郝腾飞.强噪声背景下的滚动轴承故障微弱信号检测新方法[J].轴承,2012(3):42-46.

[4] 郭玉杰,杜新定,石峰,等.滚动轴承故障的自相关函数包络分析[J].轴承,2013(6):55-58.

[5] 陈向民,于德介,李蓉,基于形态分量分析和包络谱的轴承故障诊断[J].中国机械工程,2014,25 (8):1047-1053.

[6] 李豫川,伍星,迟毅林,等.基于形态滤波和稀疏分量分析的滚动轴承故障盲分离[J]. 振动与冲击,2011，30(12):170-174.

[7] 孟涛,廖明夫.利用时延相关解调法诊断滚动轴承的故障[J].航空学报,2004,25(1):41-44.

[8] 唐贵基,王晓龙.可调品质因子小波变换在滚动轴承微弱故障特征提取中的应用[J].中国电机工程学报,2016,36(3):746-754.

[9] 张邦成,陈珉珉,尹晓静,等.基于谐波小波和 Hilbert 的滚动轴承故障诊断方法[J]. 现代制造工程,2015(6):27-30.

[10] 陈亚农,郜普刚,何田,等.局部均值分解在滚动轴承故障综合诊断中的应用[J].振动与冲击,2012,31(3):73-78.

[11] 王志武,孙虎儿,刘维雄.基于局部均值分解和奇异值差分谱的滚动轴承故障诊断研究[J].机械科学与技术,2014,33(9):1340-1344.

[12] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J] .中国电机工程学报,2012,32(11):106-111.

[13] 武哲,杨绍普,任彬,等.基于噪声辅助多元经验模态分解和多尺度形态学的滚动轴承故障诊断方法[J] . 振动与冲击,2016,35(4):127-133.

[14] 李晓晖,傅攀.基于EEMD的单通道盲源分离在轴承故障诊断中的应用[J].中国机械工程,2014,25(7):924-930.

[15] 明阳.基于循环平稳和盲源分离的滚动轴承故障特征提取方法研究[D].上海:上海交通大学,2013.

[16] 何亮.基于EMD 技术的滚动轴承故障诊断研究[D]. 大连:大连理工大学,2012.

[17] 赵光昌,谢刚,张清华.滚动轴承早期故障诊断技术[J]. 轴承,2015(6)：56-61.

[18] 时培明,许帅,李培.基于小波去噪和 EEMD 包络解调分析的滚动轴承故障诊断方法[J]. 现代制造工程, 2015(12):12-17.

[19] 王雷.基于流形学习的滚动轴承故障诊断若干方法研究[D].大连:大连理工大学,2013.

[20] 胡广书.数学信号处理理论、算法与实现[M].3版.北京:清华大学出版社,2012.

[21] 李晓鹏,席继楼,刘超,等.多重自相关在微弱低频电磁信号检测中的应用[J]. 地震地磁观测与研究，2011,32(4):44-49.

[22] 李一兵,岳欣,杨莘元.多重自相关函数在微弱正弦信号检测中的应用[J].哈尔滨工程大学学报,2004,25(4):525-528.

[23] McFadden P D，Smith J D . Vibration monitoring of rolling element bearings by the high frequency resonance technique-areview[J].TribologyInternational,1984,17(1):3-10.

[24]RandallR B,Antoni J . Rolling element bearing diagnostics-a tutorial[J]. Mechanical Systems and Signal Processing,2011,25 (2):485-520.

(编辑 李秀敏)

Fault Diagnosis of Rolling Bearings Based on Multi-Layer Autocorrelation and Envelope Analysis

ZHANG Liang1，YANG Tao2

(1.School of Mechanical and Electrical Engineering,Mianyang Normal University,Mianyang Sichuan,621000,China;2.School of Information Engineering,Southwest University of Science and Technology,Mianyang Sichuan 621010,China)

The vibration signal measured by the sensor is non-stationary and multi-component modulation signal when rolling bearings run in a fault condition. It is difficult to identify the characteristic in the presence of early bearing faults because the modulation signal is weak and polluted by noise. The multi-layer autocorrelation is used to eliminate noise while extracting signal cycle modulation component，and the envelope demodulation method based on Hilbert transform is used to obtain fault characteristic frequency and determine the type of bearing failure.The results show that the method of multi-layer autocorrelation and envelope demodulation can extract the characteristic frequency of rolling bearing more accurately, and has certain engineering application value.

rolling bearing ;multi-layer autocorrelation;Hilbert-transformation;fault diagnosis

1001-2265(2017)08-0093-04

10.13462/j.cnki.mmtamt.2017.08.023

2016-11-16

国家自然科学基金(F011102);四川中烟工业责任有限公司公司科技项目(川渝烟工技研[2015]62号)

张良(1982—)，男，四川绵阳人，绵阳师范学院助教，硕士，研究方向为机电系统故障诊断、工业自动化，(E-mail)20015601@163.com。

TH133.3；TG506

A