数控机床主轴系统动力学建模与频率特征分析*

冯吉路，汪文津，田 越

(1. 天津城建大学 控制与机械工程学院，天津 300384；2. 东北大学 机械工程与自动化学院，沈阳 110819)

数控机床主轴系统动力学建模与频率特征分析*

冯吉路1，汪文津1，田 越2

(1. 天津城建大学 控制与机械工程学院，天津 300384；2. 东北大学 机械工程与自动化学院，沈阳 110819)

文章采用集中质量法对机床主轴-滚动轴承系统进行了简化，基于Hertz接触理论计算了轴承组的等效接触刚度，建立了考虑弹性主轴刚度、阻尼和滚动轴承非线性接触力的十自由度数控机床主轴非线性振动分析模型，分析了在非平衡力作用下主轴-滚动轴承系统的非线性动力学特征。研究结果表明：当转速低于1500r/min时，主轴系统会出现由VC频率引起的拟周期运动状态；当转速为1500～7100 r/min时，主轴系统呈现周期1运动状态，系统出现了不平衡力和不对中引起的频率成分；当转速大于7100r/min时，主轴系统会出现拟周期和混沌运动状态。

主轴系统；滚动轴承；非线性动力学；稳定性

0 引言

近年来，随着高档数控机床的市场需求量的与日俱增，主轴系统的动力学特性越来越受到研究人员的关注[1]。为了避免主轴高速运转生热导致的轴承烧伤，主轴系统轴承安装时通常会留有间隙，该间隙会在轴承非线性Hertz接触力和主轴非平衡力的作用下，引起主轴系统的非线性分岔和混沌现象。为此，研究人员对主轴-滚动轴承系统进行了大量的研究。其中，Yamamoto[2]研究发现Jeffcott转子的振幅会随轴承游隙的增加而降低。Tiwari等[3]考虑了轴承的Hertz接触力、径向游隙以及主轴转动时的不平衡力的影响，分析了刚性转子的非线性动力学特性。Harsha等[4]在数学模型中加入了Hertz接触力、表面波纹度、变柔度和内部径向游隙等非线性因素，分析了平衡转子的非线性动力学特性。Lioulios等[5]分析了转子系统的非线性特性，指出速度波动对转子系统动态特性有很大的影响。Yi等[6]建立了组配轴承安装不对中问题的简化动力学模型，并提出轴承恰当的不对中安装对轴承转子系统的动力学特性可能是有益处的。曹宏瑞等[7]利用Jones轴承模型进行扩展建立滚道轴承非线性模型，得到了主轴系统的非线性动力学模型。张伟刚等[8]建立了主轴-滚动轴承的6自由度动力学方程组，得到了游隙对主轴-滚动轴承系统稳定性的影响趋势。

数控机床主轴系统的轴承多以组配形式出现，目前国内外研究人员针对主轴系统的轴承组等效接触刚度和阻尼系数的报道相对较少。然而，组配轴承的等效接触刚度和阻尼系数对主轴系统的动力学特性有重要的影响。本文在精确计算前、后轴承组等效接触刚度和阻尼的基础之上，分析了机床主轴的动力学特性，该研究相比仅考虑主轴前、后轴承处的单一轴承支承形式的计算结果更具参考价值，同时也为提高机床主轴系统的稳定性提供了理论参考。

1 主轴-轴承系统动力学建模

1.1 滚动轴承力模型

图1为滚动轴承简化模型，假定滚动体在轴承内、外圈滚道内等距分布，滚动体与滚道之间的运动为纯滚动。设滚动体与外圈沟道接触点的线速度为Vo，与内圈沟道接触点的线速度为Vi；轴承外圈沟道半径为R，内圈沟道半径为r；轴承外圈旋转角速度为ωo，内圈旋转角速度为ωi，则有：

V0=ω0×R

(1)

Vi=ωi×r

(2)

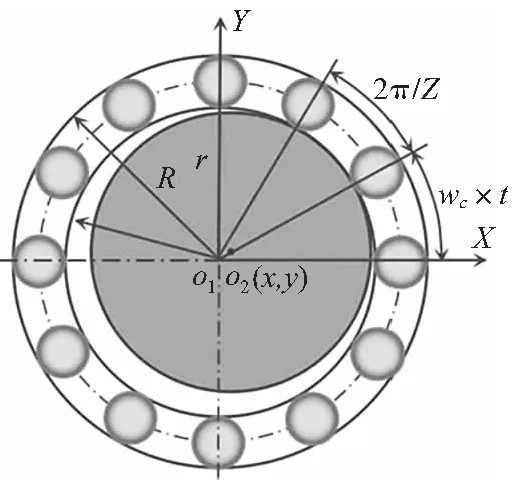
图1 滚动轴承模型示意图

保持架线速度Vc等于滚动体中心线速度，则：

(3)

由于轴承外圈固定，因此Vo=0，则：

(4)

滚动体中心的轨迹圆半径为轴承内、外圈沟道半径之和的一半，则有保持架的角速度ωc：

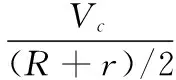
(5)

令变柔度频率为：

ωvc=ωc×Z

(6)

式中，Z为滚动体的个数。由于轴承内圈角速度ωi等于主轴的旋转角速度ω，将式(5)代入式(6)，则：

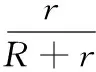
(7)

式中，BN为VC频率与旋转频率之比。设第j个滚动体处的角位置为θj，它会随时间变化而变化，其表达式:

(8)

轴承的内、外圈滚道是与滚动体相接触的，在每一个接触点，由于是Hertz接触，滚动体与滚道之间的接触变形会产生一个具有非线性特性的恢复力：

fθj=kn(rθj)n

(9)

式中，n为常数，对于球轴承，n=3/2；rθj为滚动体j在角位置为θj处的接触变形量；kn为接触刚度。在任意时刻，第j个滚动体在接触点上的弹性变形取决于滚动轴承质心的位移和轴承的初始游隙：

rθj=xsinθj+ycosθj-γ

(10)

式中，γ为轴承的初始游隙，将式(10)代入式(9)中，由轴承滚动体接触力的非负性可得：

(11)

总的接触力是每一个滚动体接触力的总和，考虑到接触阻尼cn的影响，可以得到在x和y方向上滚动轴承轴承总接触力：

(12)

由式(12)可知，轴承的接触力与主轴的轴心轨迹有紧密的联系，并且滚动轴承的刚度具有时变性，可能导致主轴-滚动轴承系统运转过程中出现混沌响应。文中前、后轴承组中的轴承参数如表1所示。

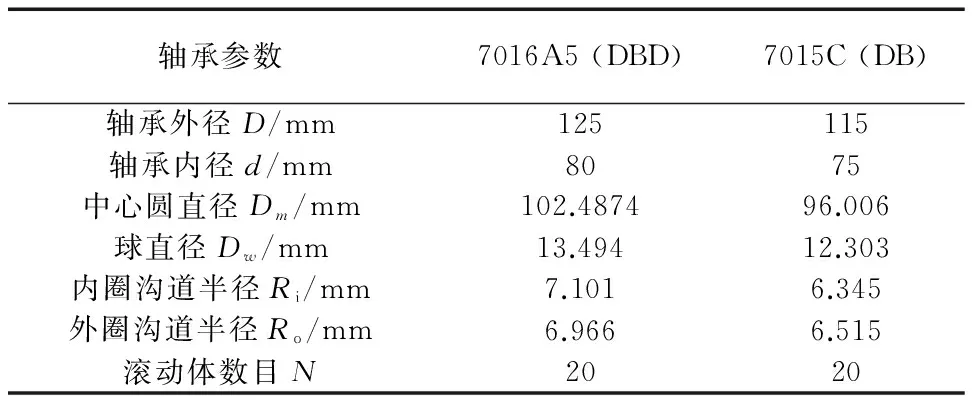
表1 角接触球轴承的原始参数

1.2 主轴-轴承系统动力学方程

为了便于分析，研究中采用集中质量法对数控机床主轴系统进行了简化，简化系统由五个集中质量单元和四个弹性轴段组成，考虑集中质量单元在X和Y方向的平动，可将该主轴-滚动轴承系统简化为十自由度系统，如图2所示。其中，非线性轴承力和转子的偏心力为系统的激励。根据牛顿第二定律，简化后主轴系统的动力学微分方程为：

(13)

系统各集中质量分别为m1=9.35 kg，m2=4.16 kg，m3=8.59 kg，m4=1.77 kg，m5=13.76 kg；转轴间的刚度系数为，阻尼系数为比例阻尼，其中c1=αk1，c2=αk2，α=0.001/ω，e=10-5m；假设成组轴承的单个轴承游隙完全相同，其中前、后轴承组单个轴承游隙分别为γ1=53.65μm和γ2=19μm。ω为主轴转速，e为主轴非平衡质量的偏心距。根据Hertz接触理论和轴承组串并联关系，计算可得前、后轴承组的等效总接触刚度分别为kn1=3.145×109N/m1.5、kn2=2.178×109N/m1.5；根据参考文献[3]，可得轴承的接触阻尼，其大小和等效接触刚度成比例定义为：

cn=0.25×10-5kn

(14)

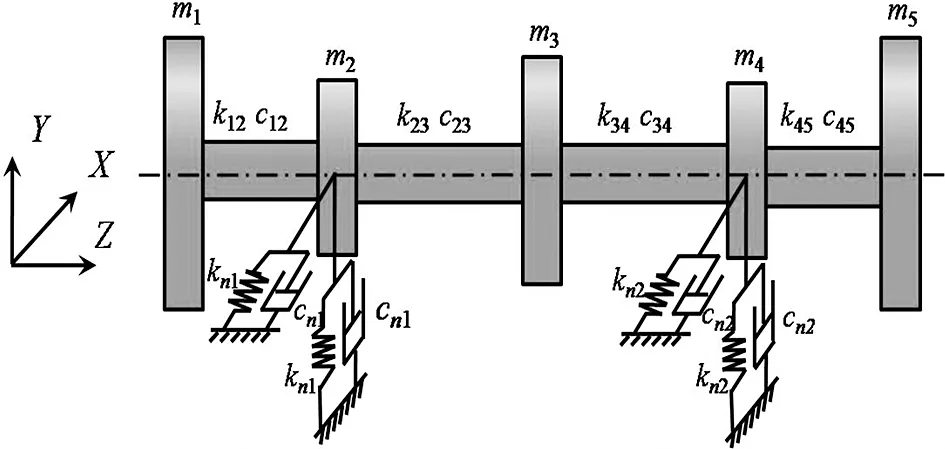
图2 机床主轴-轴承系统力学简化模型

1.3 微分方程组的无量纲化

式(13)中各个参数采用国际单位制时，由于它们之间相差很大的数量级，使得微分方程的求解变得非常困难。一般而言，对于这样的强非线性微分方程组，要用数值迭代的方法进行求解。在用数值方法求解时，假如微分方程中各个参数相差很大的数量级，就会对误差控制值和步长的选择造成很大的困难。为了解决上述困难并且使这个系统的研究成果具有广泛性与普遍性，则有必要对式(13)中各个参数进行无量纲化处理,引入无量纲量：

将上述无量纲量带入式(13),可得无量纲化后的数控机床主轴-滚动轴承系统的动力学微分方程：

(15)

2 数值模拟结果及讨论

图3为主轴系统前轴承组单个轴承的稳态径位移随转速变化的分叉图，由图分析可知，当转速低于1500 r/min时，由于轴承内圈轴心运动振幅小于1μm，此时，主轴系统的运动状态较难判断。当转速为1500～7100 r/min时，由于转速和无量纲位移存在一一对应的关系，因此主轴系统处于稳定运动状态，做周期1运动，此时主轴系统的不平衡质量在引起的不平衡力占主导作用。当转速大于7100 r/min时，系统的响应状态较为复杂，其中可能包括周期、拟周期和混沌运动状态。此时，通过分叉图基本无法判断系统的稳态响应状态。

为了进一步判断系统的稳态响应状态，本文求得了充分衰减后的最大Lyapunov指数曲线，如图4所示。由图分析可知，系统转速在7100～7250 r/min时，最大Lyapunov指数大于零，此时系统为混沌运动状态，并且系统转速等于7200 r/min时，最大Lyapunov指数取得最大值，其数值为0.0038。当系统在其它转速时，基本处于拟周期和周期运动状态。

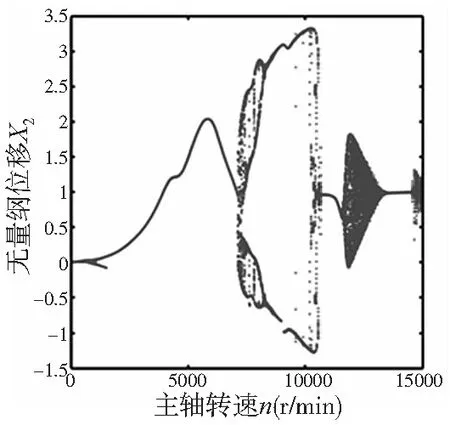
图3 主轴系统稳态响应的分叉图

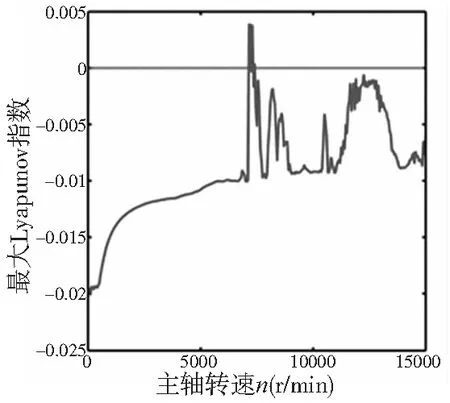
图4 最大Lyapunov指数曲线

图5为主轴转速为300 r/min时轴承内圈的轴心轨迹图及其频谱图，由图分析可知，主轴系统在转速较低时，轴承内圈轴心在一个区域内作复杂的拟周期振荡。此时频域图出现了旋转频率fw和多个VC频率成分的组合，VC振动主要是由于轴承内部刚度的周期性变化引起的；其中VC频率wvc占优表明转速较低时不平衡力和碰摩力还比较微弱。综上所述，此时系统处于拟周期运动状态。

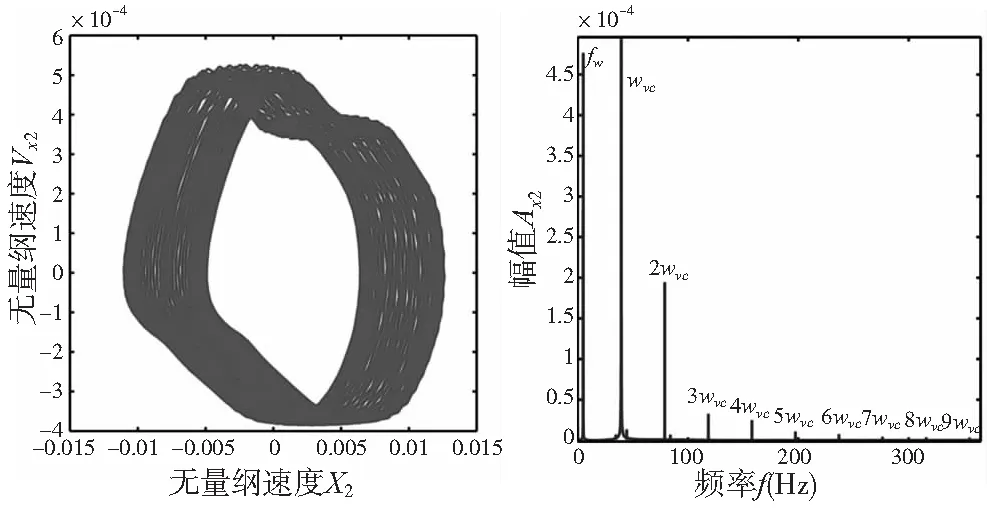
(a) 相图 (b) FFT频谱图图5 n=300 r/min时前轴承轴心径向的时频响应

图6为主轴转速为3000 r/min时轴承内圈的轴心轨迹图及其频谱图，由图分析可知，主轴系统转速为1500～7100 r/min时，轴承内圈轴心轨迹为振幅较小的一条封闭曲线，系统表现为周期1特性。此时频域图出现了旋转频率fw和二倍转频2fw的成分，其中旋转频率fw占优，这主要体现了不平衡力的作用占主导地位；二倍转频2fw是由于主轴前、后两组轴承中心线不在同一直线上，进而引起的不对中故障频率成分。

图7为主轴转速为7200 r/min时轴承内圈的轴心轨迹图及其频谱图，由图分析可知，此时轴承内圈轴心的运动轨迹较为凌乱。此时频域图出现了连续谱成分，特别是在旋转频率fw与二分之一倍频0.5fw之间的边频带成分较为复杂,出现了幅值相当且频率相差很少的成分，说明此时出现了轻微的拍振现象。最大Lyapunov指数为0.0038。通过上述分析，可以判断系统此时处于混沌运动状态。

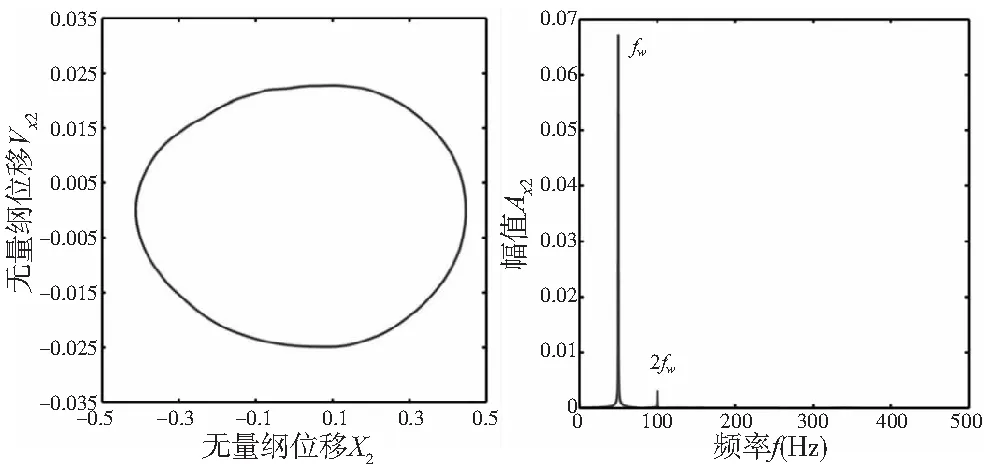
(a) 相图 (b) FFT频谱图图6 n=3000 r/min时前轴承轴心径向的时频响应

(a) 相图 (b) FFT频谱图图7 ω=7200 r/min时前轴承轴心径向的时频响应

图8为主轴转速为8200 r/min时轴承内圈的轴心轨迹图及其频谱图，由图分析可知，轴承内圈轴心轨迹呈现为内“8”字形式。此时频域图出现了0.5fw、fw、1.5fw、2fw和2.5fw等离散谱峰，说明了系统中包含了碰摩、不平衡力以及不对中等多种因素引起的频率成分；系统的主要频率成分中0.5fw占主导作用，这是碰摩故障频率成分的主要特征。

(a) 相图 (b) FFT频谱图图8 n=8200 r/min时前轴承轴心径向的时频响应

3 结论

采用集中质量法对机床主轴-滚动轴承系统进行了简化，建立了考虑弹性主轴刚度、阻尼和滚动轴承非线性接触力的十自由度数控机床主轴非线性振动分析模型，在准确计算机床主轴系统前、后轴承组等效刚度和阻尼的基础上，分析得到如下结论：(1)在非平衡力的作用下，随转速的提高机床主轴系统依次呈现了拟周期、周期、混沌和倍周期等非线性现象。

(2)低转速主轴的拟周期运动状态时，系统频率主要是由轴承内部刚度的周期性变化引起的；当主轴处于周期运动状态时，系统频率主要是由不平衡力和不对中引起的；主轴处于混沌状态时，系统频率主要是由于碰摩、不平衡力及不确定因素引起的；主轴处于倍周期运动状态时，系统中包含了碰摩、不平衡力以及不对中等多种因素引起的频率成分。

[1] 关锡友,孙伟. 数控机床主轴系统动力学特性分析方法研究[J]. 组合机床与自动化加工技术,2010 (4):1-6.

[2] Yamamoto T. On the Vibrations of a Shaft supported by Bearings having Radial Clearances[J]. Transactions of the Japan Society of Mechanical Engineers, 1955, 21:186-192.

[3] Tiwari M, Gupta K, Prakash O. Dynamic response of an unbalance rotor supported on ball bearings[J]. Journal of Sound and Vibration,2000, 238(5): 757-779.

[4] Harsha S P, Sandeep K, Prakash R. The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings[J]. International Journal of Mechanical Sciences,2003, 45(4): 725-740.

[5] Lioulios A N, Antoniadis I A. Effect of rotational speed fluctuations on the dynamic behaviour of rolling element bearings with radial clearances[J]. International Journal of Mechanical Sciences,2006, 48(8): 809-829.

[6] Yi J, Pang B, Liu H, et al. Influence of misalignment on nonlinear dynamic characteristics for matched bearings-rotor system[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics,2014, 228(2): 172-181.

[7] 曹宏瑞，李兵，何正嘉. 高速主轴动力学建模及高速效应分析[J]. 振动工程学报,2012,25(2): 103-109.

[8] 张伟刚, 高尚晗, 龙新华,等. 机床主轴-滚动轴承系统非线性动力学分析[J]. 振动与冲击, 2008, 27(9):72-75.

(编辑 李秀敏)

Dynamics Modeling and Frequency Characteristic Analysis for a Machine Spindle System

FENG Ji-lu1,WANG Wen-jin1,TIAN Yue2

(1. School of Control and Mechanical Engineering, Tianjin Chengjian Vniversity, Tianjin 300384, China；2. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

In this paper, the spindle-rolling bearing system is simplified based on lump-mass method，and the equivalent contact stiffness of bearing sets is calculated based on Hertz contact theory. A nonlinear vibration analysis model of NC machine spindle with ten freedom degrees is established, which considers elastic spindle stiffness, damping and nonlinear contact force of rolling bearing. Under the action of unbalanced force, the nonlinear dynamics characteristics of spindle-rolling bearing system is analyzed. The results show that spindle system occurs the quasi-periodic motion caused by varying compliance frequency when the rotation speed is less than 1500r/min. The spindle system presents the period-1 motion when the rotation speed is less than 7100r/min and greater than 1500r/min, and then, the frequency components of spindle system are mainly caused by the unbalanced force and misalignment. Spindle system will appear the quasi periodic and chaotic motions when rotation speed is greater than 7100r/min.

spindle system; rolling bearing; nonlinear dynamics; stability

1001-2265(2017)08-0029-04

10.13462/j.cnki.mmtamt.2017.08.007

2016-10-09；

2016-11-04

国家科技重大项目(2013ZX04011-011)

冯吉路(1988—),男,天津人,天津城建大学讲师，博士,研究方向为机床主轴动力学,(E-mail)fengjilu123@sina.com。

TH166；TG659

A