一维问题m次lagrange形函数有限元方程的条件数与预处理

张衡

（福建师范大学福清分校电子与信息工程学院，福建 福清 350300）

一维问题m次lagrange形函数有限元方程的条件数与预处理

张衡

（福建师范大学福清分校电子与信息工程学院，福建 福清 350300）

求解大型稀疏病态线性方程组是科学计算和工程应用中经常遇到的重要问题，通过预处理、降低条件数来改善病态是解决该问题的关键。在用有限元方法求解积分形式的一维两点边值问题时，利用m次lagrange形函数可将该问题的求解化成稀疏病态有限元方程组的求解。本文研究该方程组的特殊结构，分析了该方程的条件数，再将系数矩阵的大范数部分分解成4个结构特殊的简单矩阵乘积，基于这种特殊分解设计出预条件子，并对预条件子的性能进行了定量分析，结果说明该预条件子几乎不增加迭代的计算量，预处理后的条件数接近1。

病态稀疏线性方程组；lagrange形函数；特别结构；条件数；预处理

大规模稀疏线性方程组的迭代求解是科学计算和工程中经常遇到的问题[1-3]，其中方程组过高的条件数经常制约求解精度和效率，因此，在迭代求解之前，通过对方程组使用预处理技术来降低条件数，成为提高求解精度和效率的必要措施。所谓“预处理技术”是指在求解方程组时，如果A的条件数Cond(A)太大，则构造矩阵D≈A，使得D-1比A-1容易计算，D-1A的条件数 Cond(D-1A)＜＜Cond(A)，从而方程组（1）化成同解的、条件数更小的方程组

矩阵D称为预条件子或者预处理器[4]。在解决实际问题中，经常遇到高条件数（病态）的稀疏线性方程组，而且条件数随着问题规模的增加而增加[5]，成功的迭代求解，往往以适当的预条件子作为前提，否则，迭代过程可能很慢，甚至不收敛。然而，目前并没有通用的预条件子，只能针对具体问题，根据预条件子的基本要求，设计具体的预条件子[6-8]。很多计算工作者针对不同的方程组设计了不同的预条件子，但是对预条件子的性能（条件数下降的程度，预处理后的条件数，对计算量的影响等），多以计算结果说明，鲜见有定量的分析结果[9-15]。

使用有限元方法，求解积分形式的两点边值问题时，基于m次lagrange形函数形成的有限元方程，属于稀疏线性方程组，其总刚度矩阵有特别的结构。针对这种结构，本文讨论了该方程的条件数，并设计出预条件子，定量分析了预条件子的性能。

1 m次lagrange形函数有限元方程的形成

根据问题（1）离散形式的矩阵表达式（8）得：

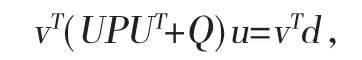
从而得到有限元方程

总刚度矩阵为：

将总刚度矩阵写成分解的形式（10），可以避免刚度矩阵的拼接计算，而且有利于分析条件数，有利于设计预处理子和算法。

2 有限元方程的条件数

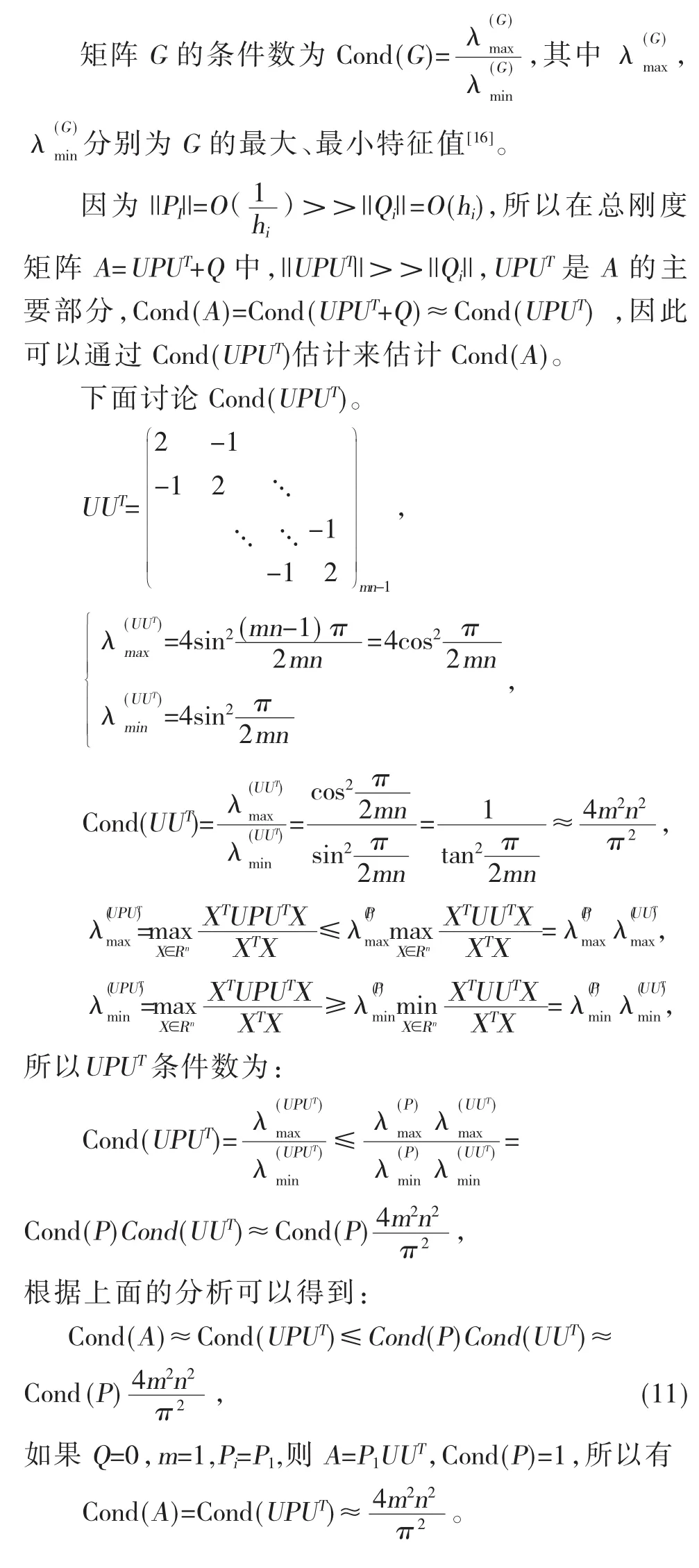
显然在总刚度矩阵A=UPUT+Q中，U有特别的作用，U如同条件数的放大器，将条件数从Cond(P)放大到因此U是造成A有高条件数的重要原因。

3 有限元方程的预处理

如果使用迭代法求解方程（9），则因方程（9）的条件数很大，可能不收敛，必须进行预处理降低条件数。因为 ||UPUT||＞＞||Qi||，所以 1＞＞||(UPUT)-1Q||，Cond[I+(UPUT)-1Q]≈Cond(I)=1，因此选择UPUT为预条件子，将有限元方程（9）化成

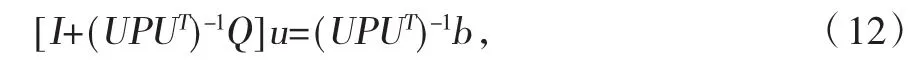
根据式（12），取迭代式为

预条件子UPUT是否合适，不仅要看它是否能够降低条件数，更重要的是看它是否会导致计算量的增加。求解方程（13），主要的计算量是（UPUT）-1与向量的乘积。本文通过分析UPUT的结构，研究（UPUT）-1与向量的乘积的计算量。

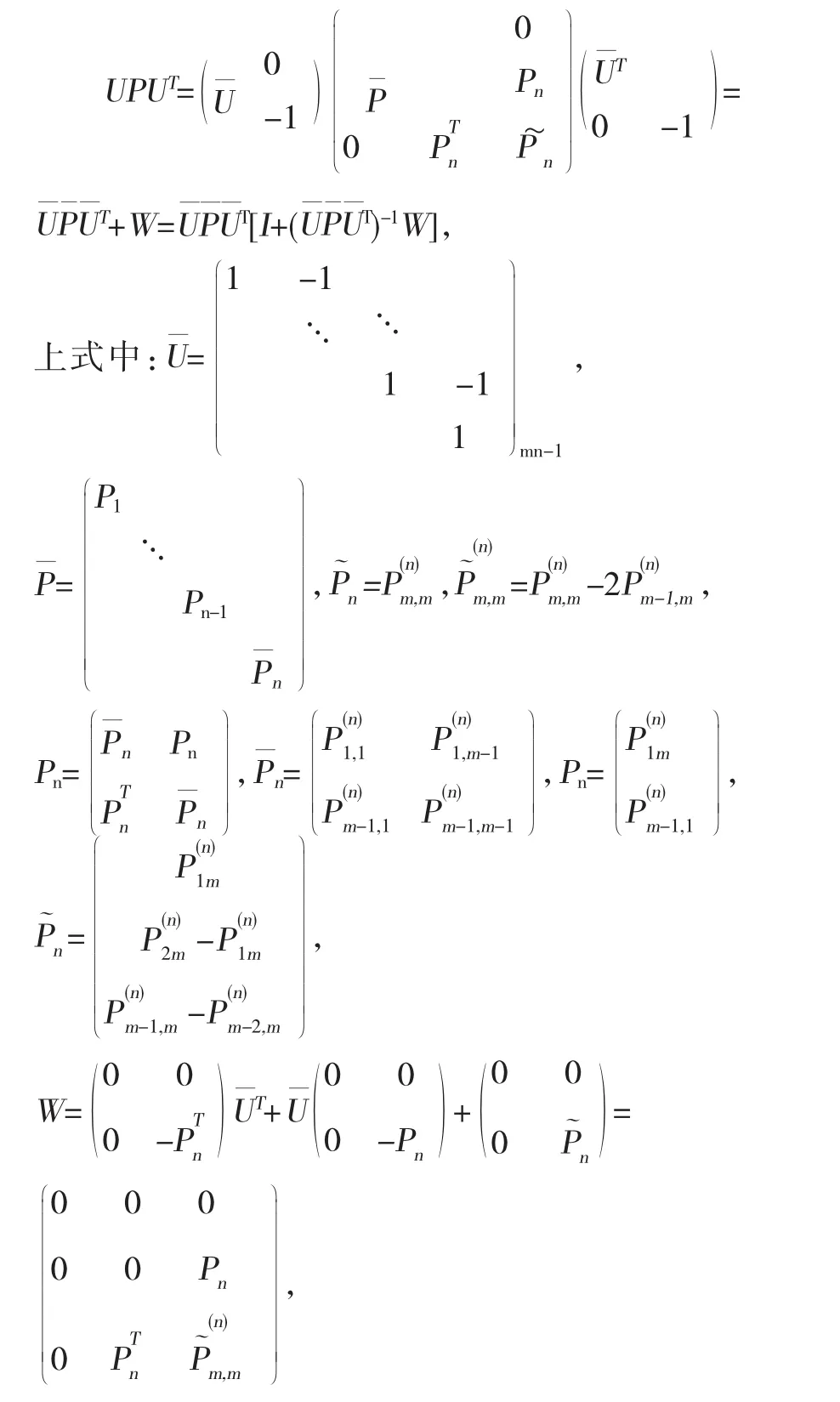
4 结语

稀疏线性方程组的稀疏性，往往隐含着简单的结构，这些简单的结构并不是显然的，所以没有显然、通用的预处理方法，通常要针对具体的问题找到这些特别的简单结构，才能发现影响条件数的主要原因，并提出合适的预处理方法。

使用有限元方法求解积分形式的两点边值问题时，基于m次lagrange形函数形成有限元方程，本文通过研究该方程总刚度矩阵的结构找到了影响条件数的主要原因，并针对该方程总刚度矩阵的特别结构，将刚度矩阵的大范数部分，分解成4个结构简单的矩阵乘积，从而提出预处理方法，使条件数接近1，而且与一般的迭代法相比，不需要过多的计算量。

[1]Jia Z X,The Convergence of Krylov Subspace Methods for Large Nonsymmertric Linear Systems[J].Acta Mathematical Sinica,1988,14(4):507-518.

[2]Van Der Vorst H A,Dekker K.Conjugate Gradient Type Methods and Preconditioning[J].Journal of Computational and Applied Mathematics,1988,24(1):73-87.

[3]Yong D M,Jea K C.Generalized Conjugate-Gradient Acceleration of Nonsymmetrizable Iterative Methods[J].Linear Algebra Appl,1980,34:159-194.

[4]李荣华.偏微分方程数值解法[M].2版.北京：高等教育出版社，2010：139-140

[5]周志阳，聂存云，舒适.一种二阶混合有限体元格式的GAMG预条件子[J].计算物理,2011,28(4):493-500.Zhou Zhiyang，Nie Cunyun,Shu Shi1.An Effcient GAMG-based Preconditioner for Second Order Mixed-type Finite Volume Element Method[J].Chinese Journal of Coputational Physics,2011,28(4):493-500.

[6]Bai Z Z,Li G Q.Restrictively Preconditioned Conjugate Gradient Methods for Systems of Linear Equations,IMA Journal of Numerical Analysis 2003(23)：561-580

[7]Wang Z Q.Restrictively Preconditioned Chebyshev Method for Solving Systems of Linear Equations[J].Eng Math，2015 93,61-76

[8]Rafael Bru,Jos?e Mar?in,Jos?e Mas,et al.Preconditioned Iterative Methods for Solving Linear Least Squares Problems[J].SIAM J Sci Comput,2014,36(4)：2002-2022.

[9]于春肖,苑润浩,穆运峰.新预处理ILUCG法求解稀疏病态线性方程组[J].数值计算与计算机应用,2014,35(1):21-27.Yu C X,Yuan R H,Mu Y F.New Preconditioning ILUCG Method for Solving Sparse Ill Conditioned Linear Equations[J].Journal on Numerical Methods and Computer Applications,2014,35(1):21-27.

[10]Xue Q F,Gao X B,Liu X G，Comparison Theorems for a Class of Preconditioned AOR Iterative Methods[J].Journal of Mathematics,2014,34(3):448-460.

[11]潘春平,马成荣,曹文方,等.一类预条件AOR 迭代法的收敛性分析[J].数学杂志,2013,33(3):479-484.Pan Chunping,Ma Chengrong,Cao Cenfang,et al.On Convergence of a Cype of Preconditional AOR Iterative Method[J].Journal of Mathematics,2013,33(3):479-484.

[12]罗芳.L-矩阵的多参数预条件AOR迭代法[J]数学的实践与认识,2013,43(15)：277-282.Luo F.On the Ulti-parameter Precondition AOR Iterative Method for L-matrices[J].Mathematics in Practice and Theory,2013,43(15)：277-282.

[13]吴建平,赵军,马怀发,等.一般稀疏线性方程组的因子组合型并行预条件研究[J].计算机应用与软件,2012,29(5):6-9,108.Wu J P,Zhao J,Ma H F,et al.General Sparse Linear Equations System Factor Combined Parallel Precondition Research[J].Computer Applications and Software,2012,29(5):6-9,108.

[14]李继成,蒋耀林.预条件IMGS迭代方法的比较定理[J],数学物理学报,2011,31A(4):880-886.Li J C,Jiang Y L.Comparison Theorems of the IMGS Iterative Method wtih Preconditioner[J].Acta Mathematica Scientia,2011,31A(4):880-886.

[15]Pan Chunping.A new Effective Preconditioned Gauss_Seidel Iteration Method[J].Journal on Numerical Methods and Computer Applications,2011,32(4):267-273.

[16]林群.微分方程数值解法基础教程[M].2版.北京：科学出版社,2003：87-111.

Condition number and preprocess of the finite element equation of one dimensional problem with m-degree lagrange shape function

Zhang Heng
(School of electronic and Information Engineering,Fuqing Branch of Fujian Normal University,Fuqing,Fujian 350300,China)

Solving the large sparse ill-conditioned linear equations is very important in scientific computing and engineering applications.Reducing the condition number by preprocessing is the key to it.The finite element equations formed in solving two-point boundary value problems with integral form using finite element method based on m-degree lagrange shape function are discussed.The condition number of the finite element equations is analyzed by studying the special structure of the equation.The part of the coefficient matrix with big norm is decomposed into product of four simple structure matrices.The preconditionerwas obtained based on the decomposition,and performance analysis ofthe preconditionerwas given quantificationally.The results of analysis show that the condition number is close to 1 after pretreatment without causing more computing.

sparse ill-conditioned linear equations;lagrange shape function;special structure;condition number;preprocess method.

O241.6

A

10.13880/j.cnki.65-1174/n.2017.04.021

1007-7383(2017)04-0518-04

2016-03-13

福建省自然科学基金项目(2014J01006)

张衡，男，（1961-），教授，从事微分方程数值解以及并行计算方法与应用研究，e-mail:zhheng01@163.com。