打拿极材料二次电子发射系数计算模型研究现状

何一蕾，王多书，郭 磊

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

打拿极材料二次电子发射系数计算模型研究现状

何一蕾，王多书，郭 磊

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

电子倍增器使用寿命短的问题严重制约了其在导航定位系统中的应用，究其根本原因在于现有电子倍增器增益低，且打拿极材料在轰击能量较高的离子或较强电子束流长期作用下耐轰击能力弱，增益衰减过快。通过对国内外研究人员提出的打拿极二次电子发射系数计算模型进行详细分析，总结了这些模型的优缺点，提出建立打拿极材料二次电子发射系数计算模型的启示和建议。

电子倍增器；打拿极材料；二次电子发射系数；计算模型

0 引言

二次电子发射是指具有一定能量或速度的电子（或离子）轰击物体表面引起物体表面发射电子的物理过程[1]。二次电子发射过程中，二次电子数目与原电子数目的比值称为二次电子发射系数，是影响电子倍增器增益的主要因素，其大小与材料性能和入射条件等因素有关[2]，二次电子发射系数大，则电子倍增器的增益就高。

近年来，电子倍增器已广泛用于导航定位、深空探测及微光夜视成像等技术领域[3-4]。铯原子钟是导航定位系统及深空探测器中的关键设备，其准确度是衡量空间定位精度的关键指标，像增强器是微光夜视仪的重要器件，其性能直接影响着微光夜视效果。电子倍增器是铯原子钟和微光夜视像增强器的重要部件，工作时利用电场加速由前级打拿极材料发射的二次电子，使其进入后级打拿极发射层激发出更多二次电子，通过依次串联多级打拿极，实现电子束流逐级放大，从而提高铯原子钟的准确度和像增强器的信噪比等性能指标。电子倍增器使用寿命短的问题严重制约了其工程中的应用，根本原因在于现有电子倍增器增益低，且打拿极材料在轰击能量较高的离子或较强电子束流长期作用下耐轰击能力弱，增益衰减过快。其中电子倍增器的增益是衡量其使用寿命的主要指标，与各打拿极对应的二次电子发射系数有关，二次电子发射系数计算模型可以定量描述二次电子发射系数的高低，从而对倍增器的增益进行计算。

具有较高的二次电子发射系数对于打拿极发射层材料而言非常重要，相对其他材料，氧化物材料二次电子发射系数高、热稳定性好、耐轰击能力强，是最有希望获得长寿命使用特性的材料之一[5-7]，目前铯原子钟及微光夜视仪等产品的电子倍增器通常采用氧化物作为打拿极材料。由于打拿极材料二次电子发射过程较为复杂，多年来研究人员一直在努力探索打拿极材料二次电子发射过程，试图通过建立发射模型来定量描述二次电子发射现象，计算分析并确定影响电子倍增器使用寿命的因素，先后发展的多种模型虽然可以部分或半经验的解释一些实验事实，但距离彻底解决电子倍增器使用寿命短的问题还有较大差距。文章通过对现有二次电子发射系数计算模型进行分析研究，总结各模型的优缺点，为后续建立打拿极材料二次电子发射系数计算模型提供参考。

1 二次电子发射系数计算模型

电子倍增器的增益高，则使用寿命长，因而研究打拿极材料二次电子发射特性对于延长倍增器使用寿命至关重要。随着二次电子发射研究的不断深入，很多研究者根据二次电子发射的主要物理过程和特性建立了打拿极二次电子发射系数计算模型，通过模型可以较准确的获得二次电子发射系数曲线，再使用控制变量法，明确打拿极材料二次电子发射系数与入射能量、入射角度、材料特性等因素间的关系，揭示二次电子发射机理。

1.1 Dekker模型

Dekker[8]在总结研究经验的基础上提出了二次电子发射系数简化模型，原电子入射到物体表面后，入射电子将能量传递给物体内部电子，引起内部电子的激发。一个初始能量为EPE的原电子在发射体内行进的过程中，若在发射体中最大入射深度为R，则二次电子发射系数的数学表达式为：

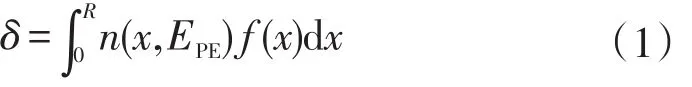
式中：x为原电子入射深度；n( ) x,EPE为一个初始能量为EPE的原电子在深度x处单位路径上所激发产生的二次电子数[9]，与原电子射入物体后的能量损失规律密切相关，即：

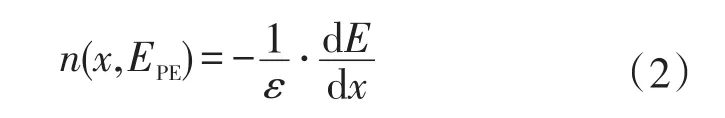
式中：ε为激发产生一个二次电子时原电子损失能量的平均值；E为入射电子在x处的能量。

f（x）表示深度x处激发产生的二次电子转移到表面后克服表面势垒逸出的几率[10]：

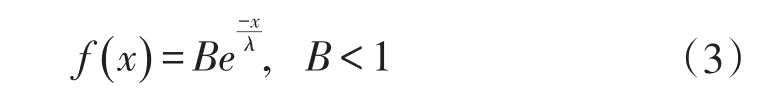
式中：λ为平均电子逸出深度；B为x=0时的逸出几率，与材料特性相关。

Young[11]研究了厚度为12～175μg/cm2的Al2O3样品在入射电子为2.5～10 keV时电子能量随深度的衰减，结果表明，单位厚度损失的平均能量在整个入射深度上几乎保持恒定，因而：

因此二次电子发射系数修正为：

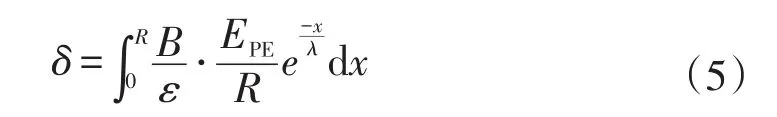
Simon等[12]利用模型研究了低能电子入射下金属Pt、半导体Ge和绝缘体MgO的最大二次电子发射系数值，在相同能量的电子入射下MgO具有更高的二次电子发射系数值，与相关文献中的试验结果相同，还给出了产生最大二次电子发射系数δmax时对应的入射能量、入射深度等参数。

Young[11]对电子在Al2O3样品中的入射深度R进行测定后引入到Dekker模型中，并对积分后的模型进行归一化处理后提出低能电子下通用计算模型：

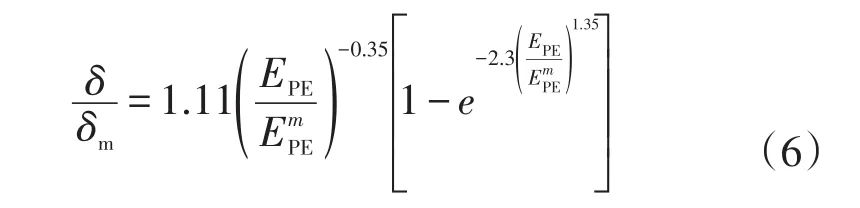
Lint等[13]对入射深度R变换运算方法，通过Young的计算思想给出了不同的基于实验校准曲线的计算模型：

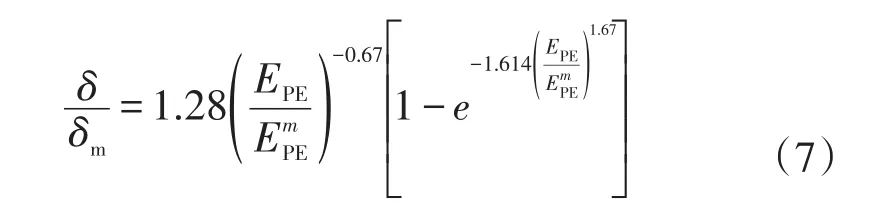
式中：δm为最大二次电子发射系数；EPE为原电子的初始能量为最大二次电子发射系数对应的能量值，模型中δ/δm与材料的常数B、ε和ρ无关。

模型式（6）和式（7）通常被称为“二次电子发射系数普遍定律”，如果不存在δm和Em的可靠理论值或试验数据，则可以通过蒙特卡罗模拟获得这些数据，进而采用经验模型对新型材料的二次电子发射系数进行量化计算，为更好的研究二次电子发射系数提供有效的参考。

Insepov等[14]总结了Lin等的研究，并用Dekker模型结合蒙特卡罗方法对微通道板（MCP）中打拿极材料（Al2O3）在初始能量E=50～2 000 eV入射角度0°≤θ≤89°的条件下进行模拟计算，与以往研究结果对比发现模拟结果会因样品的不同而有所差异，表面粗糙度小的样品比粗糙度大的样品最大二次电子发射系数高出18%。此研究中有关Dekker模型在低能条件下的参数化工作仍然有待完善，且以上研究并未涉及离子轰击能量较高时的情况。以上方法还可应用于研究Al2O3、ZnO和MgO等具有较高发射系数材料在其各自不同状态下对二次电子发射系数的影响，进而寻求最佳工艺参数，以提高打拿极二次电子发射稳定性。

Reimer等[15]研究了10～100 keV电子入射下Al膜和Au膜的二次电子发射系数，并推导了平均逸出深度等参数与金属的二次电子发射系数之间的关系。谢爱根等[16]在其基础上结合模型式（5）深入研究了0.8～10 keV的金属二次电子发射系数，根据射程与能量的关系，确定金属材料在原电子入射能量为0.8～10 keV范围内n、A值并代入Dekker模型，积分得出二次电子发射系数与试验结果之间的通用模型δ0.8～10（下标表示原电子的能量范围）为：

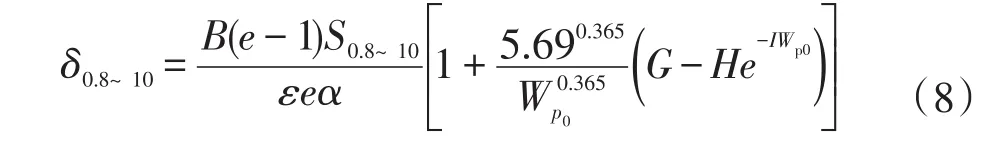
式中：S0.8～10=d Wp/d x、Wp0为原电子能量；α为吸收系数；B为x=0时的逸出几率，与材料特性相关；A由发射体的密度和原子序数决定；G、H和I为金属在能量范围0.8～10 keV内的特性参数。

通过测量Au和Ag在0.8～10 keV能量入射下的二次电子发射系数与模型计算值之间有较好的一致性，该模型的准确性得到进一步验证。还发现同种类的金属在不同制备条件下得到的二次电子发射系数值不同。该模型中很多系数都是金属特性下计算得到的，因此并不适用于氧化物材料的计算，但是其对较强电子束流入射情况下的计算方法可以对打拿极材料二次电子发射计算模型的建立提供参考。

Dekker模型结构简单，衍化公式较多，可以用于计算氧化物、金属等材料的二次电子发射系数，对低能电子入射下二次电子发射的物理过程研究较多，得到的计算曲线与试验结果较符合。Dekker模型更多的考虑了二次电子发射系数值的计算，忽略了电子产生与逸出过程的具体细节，因此并不能准确的预测给定初始能量下材料的二次电子发射系数。尤其是较强电子束流入射时，研究大多集中在金属材料，对于氧化物材料尚未给出较为准确的计算模型。

1.2 Vaughan模型

Vaughan模型是基于概率统计的二次电子发射模型，二次电子在出射数目、出射能量和出射角度上均具有一定随机性。20世纪末期，Vaughan[17-18]在Dekker等的研究基础上，结合Shih等的试验数据，构造与试验数据曲线相吻合的拟合函数，最终给出了二次电子发射系数的分段计算模型：

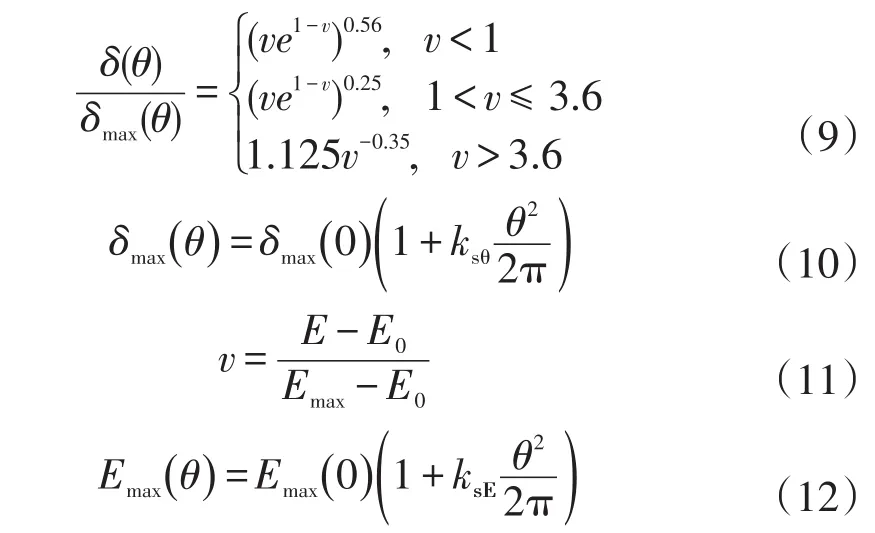
式中：v为阈值因子；θ为入射电子与碰撞表面法向的夹角；δm（0）为原电子垂直入射时的最大二次电子发射系数；E为入射电子的能量；E0为二次电子发射阈值；Emax为产生最大二次电子发射系数时对应的入射电子能量；ks为表面光滑度因子。

游检卫等[19]对Vaughan模型进行理论扩展，采用Furman模型的能谱处理方法，研究并补充了二次电子出射能量和出射角度的计算方法。假定每个电子的出射能量不大于入射能量的1/n、n为出射电子数目，经过大量实验数据的拟合分析，出射电子能量的概率密度分布符合伽马概率密度函数分布：

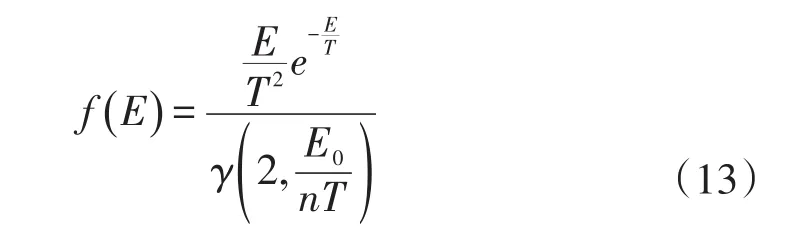
利用概率密度函数与分布函数的关系，求出电子出射能量的分布函数F()

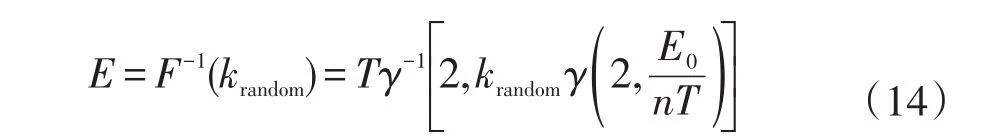
式中：E为二次电子的出射能量；krandom为在[0，1]之间均匀产生的随机数；E0为电子入射能量；n为出射电子数目；T为材料表面温度；γ（x，y）为不完全伽马函数。

电子出射角度包括方位角ϕout∈[0.2π]和俯仰角θout∈[0,π2]，其中方位角的概率分布满足均匀概率密度函数，俯仰角需要求解余弦概率密度函数的反分布函数，最终确定出射角度的表达式为：

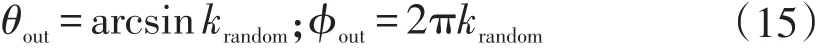
该研究补充了传统Vaughan模型中缺少二次电子出射能量与出射角度等参数的不足，使得对数值模拟更为便捷，为后续模拟计算工作提供了有效参考，并采用不同能量电子垂直轰击金Ag表面后发E，通过求解分布函数的反函数得到电子的出射能量：现，所得二次电子出射能量曲线与理论计算结果基本吻合，拓展后Vaughan模型算法的准确性得到了进一步验证。

Vaughan模型与初始入射能量E和入射角度θ有关，并且引入了表征材料表面粗糙度的光滑度因子，模型结构简单、便于仿真、精度较高。Vaughan模型只限于对低能条件下的试验数据进行较准确拟合，在高能量范围内拟合偏差较大。Vaughan模型及其拓展形式可以为打拿极材料二次电子发射系数提供精确的计算方法，但该模型偏向数学分析计算，模型参数缺乏相关试验数据支撑，因此不便于引入新的参量对打拿极二次电子发射系数进行修正。

1.3 Furman模型

2002年，Furman等[20]提出了二次发射概率模型，该模型主要从物理机理出发，首次将二次电子细分为真二次电子、弹性散射电子以及非弹性散射电子，真二次电子模型如式（16）：

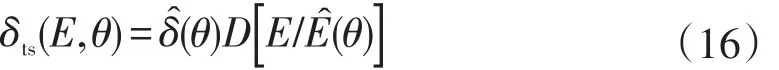
Furman模型更偏向于物理机理的阐释，根据二次电子的不同分类建立了对应的二次电子发射模型，是目前最精确的模型。但是其表达式比较复杂，该模型用在高能电子入射条件下与试验数据不够吻合，具体原因尚不明确，对于不同材料、初始能量和入射角的二次电子发射能谱的拟合没有统一的参数调节标准，适用性相对较差。

1.4 普适函数模型

Guest等[21]通过理论经验分析与试验数据相结合的研究发现，对于表面纯净的固体而言，其二次电子发射特性可以利用拟合后的函数进行有效模拟，并将其称为二次电子发射普适函数：

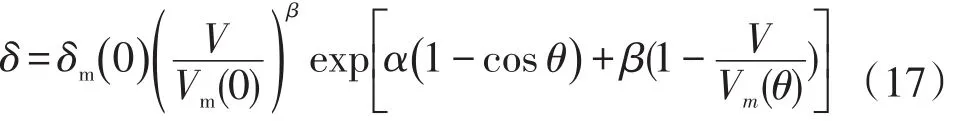
式中：δm（0）为原电子垂直入射时的最大二次发射系数；θ为入射电子与入射表面法向的夹角；Vm（0）为原电子垂直入射时相应的加速电压；V为原电子加速电压；Vm（θ）为入射角为θ时产生最大二次电子发射系数时对应的加速电压；α为材料表面特性常数；β为函数曲线形状参数。

彭玲玲等[22]以SiO2作为微通道板（MCP）打拿极的二次电子发射层，对上述模型进行模拟计算，确定SiO2的二次电子发射系数δ与入射角度θ和入射加速电压V三者之间的关系，在理想条件（表面光滑、不受逸出功和温度的影响）下，原电子入射角或原电子加速电压适当变大时可以增大二次电子发射系数δ。

该模型中既考虑了材料特性和表面结构对二次电子发射系数的影响，也考虑了入射电子能量和入射角等因素，能够较准确的计算低能电子入射时纯净固体表面的发射系数，因此在打拿极材料二次电子发射系数的计算中得到了很广泛的应用，但是对于离子轰击能量较高时并不适用。如果能将温度、表面光滑度、薄膜厚度等主要参数引入模型，模拟结果与实际测量值间的吻合度将会更好。

1.5 多层膜计算模型

Yu等[23]对低能电子入射下多层膜结构的二次电子发射系数进行了研究，当单一膜层厚度较薄时，多层膜结构的二次电子发射系数值近似为每层薄膜产生的二次电子发射系数之和：

将入射电子穿透第m层末端的能量表达式代入Dekker模型，数学积分后得到双层膜二次电子发射系数计算模型：

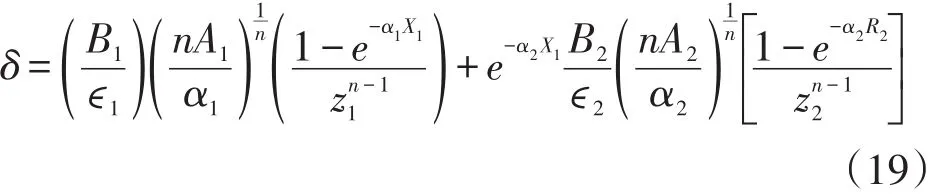
Yu等利用该模型对Si衬底上的SiO2膜层进行计算，得到数据与试验结果基本吻合。郭金川等[24]借鉴Yu等推导的模型分析了微通道板（MCP）打拿极发射层二次电子发射特性，分别计算出入射电子能量为0～1 keV时，不同膜厚SiO2/Si、Al2O3/Si、MgO/Si双层膜材料的二次电子发射系数。当初始电子能量较低时，二次电子发射系数变化趋势会偏离理论曲线，相反当初始能量较高时，则与曲线相符。该模型对打拿极多层膜结构的优化提供了理论参考，但是只考虑了电子的逸出深度和膜层厚度，忽略了电荷的积累，导致计算结果有所偏差。

2 结论

二次电子发射系数计算模型在打拿极材料二次电子发射性能研究中有非常重要的作用。在材料方面，多数模型基于金属材料，而对氧化物材料的二次电子发射模型模拟较为匮缺。在入射能量方面，很多二次电子发射模型是基于低能电子（或离子）入射条件下提出的，现有打拿极材料常用的Dekker模型、普适函数模型、多层膜结构模型并不满足高能量入射条件，计算数据与试验结果间存在偏差，导致不能对增益衰减规律进行准确预测，很难对解决电子倍增器使用寿命问题提出有效参考。

对于氧化物材料二次电子发射数值模拟研究，需要对影响二次电子发射性能的物理因素进行综合考虑，以现有二次电子发射系数计算模型为基础，开展在轰击能量较高的离子或较强电子束流入射下的验证试验，进一步揭示氧化物材料二次电子发射物理机理，不断通过试验对模型进行验证和优化，得出打拿极材料二次电子发射系数新模型。

较强电子束流入射时建议采用普适函数模型，该模型对材料特性、入射条件等因素考虑较为全面，但该模型是基于理想条件建立的，未将实际试验中涉及到的温度、导电性、薄膜厚度等因素考虑在内，因此在该模型基础上引入以上重要影响因素，对其进行进一步优化以满足试验验证条件。离子轰击能量较高时可以借鉴金属二次电子发射系数计算模型的研究方法，对离子入射的物理过程进行分析，结合打拿极材料特性，在Dekker模型的基础上，引入适当因素，建立新的计算模型。

[1]承欢，江剑平.阴极电子学[M].西安：西北电讯工程出版社，1986：164.

[2]Straka E R.Performance Characteristics of Cesium Beam Tube Electron Multipliers[C]//36th Annual Frequency Control Sym⁃posium，1982：230-235.

[3]陈江，李得天，王骥，等.导航铯原子钟的发展现状及趋势[J].国际太空，2016（448）：20-24.

[4]郭晖，向世明，田民强.微光夜视技术发展动态评述[J].红外技术，2013，35（2）：63-68.

[5]张洋，黄永刚，刘辉，等.阳极氧化铝微通道板研究的进展[J].红外技术，2012，34（7）：427-432.

[6]李晨，罗崇泰，王多书，等.MgO二次电子发射功能薄膜的制备方法[J].真空与低温，2009，15（4）：187-192.

[7]冯娜，杨生胜，陈益峰，等.空间材料二次电子发射过程的理论研究[J].真空与低温，2013，19（3）：145-149.

[8]Lye R G，Dekker A J.Theory of secondary emission[J].Physi⁃calReview，1957，107（4）：977.

[9]Joy D C.A model for calculating secondary and backscattered electronyields[J].JournalofMicroscopy，1987，147（1）：51-64.

[10]Kanaya K，Ono S，Ishigaki F.Secondary electron emission from insulators[J].Journal of Physics D：Applied Physics，1978，11（17）：2425.

[11]Young J R.Penetration of electrons in Al2O3-films[J].Phys Rev，1956，103：292-293.

[12]Simon R E，Williams B F.Secondary-Electron Emission[J]. IEEE Transactions on Nuclear Science，1968，15（3）：167-170.

[13]Lin Y，Joy D C.A new examination of secondary electron yielddata[J].SurfaceandInterfaceAnalysis，2005，37（11）：895-900.

[14]Insepov Z，Ivanov V，Frisch H.Comparison of candidate sec⁃ondary electron emission materials[J].Nuclear Instruments and Methods in Physics Research Section B：Beam Interac⁃tionswithMaterialsandAtoms，2010，268（20）：3315-3320.

[15]Reimer L，Drescher H.Secondary electron emission of 10-100 keV electrons from transparent films of Al and Au[J]. JournalofPhysicsD：AppliedPhysics，1977，10（5）：805.

[16]Xie A G，Xiao S Y，Wang L.Formulae for the secondary elec⁃tron yield and total stopping power from 0.8 keV to 10 keV formetals[J].Pramana，2016，86（5）：1127-1141.

[17]Vaughan R.A new formula for secondary emission yield[J]. IEEETrans，ElectronDevices，1989，36（9）：1963-1967.

[18]Vaughan R.Secondary emission formulas[J].IEEE Trans. ElectronDevices，1993，40（4）：1963-1967.

[19]游检卫，张剑锋，李韵，等.Vaughan二次电子发射模型的深入研究与拓展[J].强激光与离子束，2013，25（11）：3035-3039.

[20]Furman M A，Pivi M T F.Probabilistic model for the simula⁃tion of secondary electron emission[J].Physical Review Spe⁃cialTopics-AcceleratorsandBeams，2002，5（12）：124404.

[21]Guest A J.A computer model of channel multiplier plate per⁃formance[J].ActaElectronica，1971，14（1）：79-97.

[22]彭玲玲.微通道板薄膜打拿极二次电子发射特性研究[D].长春：长春理工大学，2014：38-42.

[23]Yu S G，Yi W，Jeong T，et al.Secondary electron emission for layeredstructures[J].JournalofVacuumScience&Technolo⁃

REVIEW ON THECOMPUTATIONALMODEL OFSECONDARY ELECTRON EM ISSION YIELD FOR DYNODEMATERIAL

HEYi-lei，WANG Duo-shu，GUO Lei
（Scienceand Technology on Vacuum Technology and Physics Laboratory，Lanzhou Institute of Physics，Lanzhou 730000，China）

The application of electron multiplier in navigation and positioning is seriously restricted by its short lifetime. The fundamental cause is that the gain of the electron multiplier is low and the resistance of the dynode material to bombardment becomes weaker and weaker when operated under high energy ions or strong electron beam conditions. The computational models of secondary electron emission yield proposed by domestic and overseas researchers were analyzed. The advantages and disadvantages of those models were summarized，and some relevant revelations and suggestions were furtherly put forward to establish the computational model of secondary electron emission for the dynode material.

electron multiplier；dynode material；secondary electron emission yield；computational mode

O462.2

：A

：1006-7086（2017）04-0207-05

10.3969/j.issn.1006-7086.2017.04.004

2017-05-04

何一蕾（1993-），女，甘肃天水人，硕士研究生，主要从事光学薄膜技术研究。E-mail：wang_d_s@163.com。