基于分数阶小波变换与QR分解的盲数字水印算法

李 茜 卓智海 汪毓铎

（北京信息科技大学信息与通信工程学院，北京 100101）

学术探讨

基于分数阶小波变换与QR分解的盲数字水印算法

李 茜 卓智海 汪毓铎

（北京信息科技大学信息与通信工程学院，北京 100101）

通过对现有的盲数字水印算法的研究，本文提出一种新颖的基于分数阶小波变换(FRWT)和QR分解的盲数字图像水印算法，相比于现有的基于DWT域数字图像水印方法，该方法兼具分数阶小波变换(FRWT)和DWT的优点，对数字水印处理具有更高的灵活性。仿真结果表明嵌入水印后的宿主图像的峰值信噪比均高于40dB，充分说明该算法不仅可以很好地平衡水印的不可见性，而且对几何攻击具有较好的鲁棒性。

数字图像水印；分数阶小波变换(FRWT)；分数阶Fourier变换；QR分解

1 引言

随着科技的发展，人们进入了一个能够迅速获取和交流信息的数字化、网络化时代，在给人们带来便利的同时，一些有价值的信息容易遭到复制、篡改。因此，如何识别信息的真伪、保护信息的版权等成了这个时代亟待解决的信息安全问题。作为对信息版权保护的一种有效途径，数字水印技术应运而生，它分为空域水印技术和变换域水印技术。在变换域中嵌入水印不仅能提高水印的不可见性，而且其鲁棒性要比空域的算法好，因此变换域水印技术更受关注。在变换域水印技术中，离散余弦变换(DCT)、离散小波变换(DWT)、离散傅里叶变换(DFT)、离散分数阶傅里叶变换(DFRT)、极坐标谐波变换(PHT)以及离散线性正则变换(LCT)等应用广泛，受到了很多学者的青睐[1-7]。DWT和其他变换相结合的水印方法既包含有DWT的多分辨率思想和时频局域化等优点，也兼备其他变换的优势，所以它们成为数字图像水印领域的研究热点。

近几年出现了基于DWT和矩阵分解的水印技术，比如DWT和QR分解、奇异值分解(SVD)、LU分解、Schur分解等矩阵分解方法相结合，而且己经被证明基于DWT和矩阵分解的水印技术可以在不可见性和鲁棒性之间做一个很好的平衡，特别是具有明显的抗几何攻击效果[11–15]。分数阶小波变换(FRWT)是经典DWT和分数阶傅里叶变换(FRFT)的结合，它兼具DWT和FRFT的优点，具有在FRFT域多分辨表征图像的能力[16,17]。这些良好的性质使FRWT成为一个图像处理领域重要的数学工具之一，它己经被成功应用于图像融合和图像去噪。因此，非常有必要研究FRWT在数字水印领域潜在的应用优势。

2 相关理论基础

2.1 分数阶小波变换

分数阶小波变换的定义为[15]：

其中ψa,b(t)是传统小波变换的母小波，a，b分别为尺度因子和时移因子。当θ=π2时，FRWT退化为经典的小波变换。

推广一维FRWT到二维FRWT，其定义为：

2.2 QR分解

任意非奇异M×N阶矩阵A可以分解为两个矩阵的乘积，即

其中Q是M×N正交矩阵，R是N×N阶非奇异上三角矩阵，而且除去相差一个对角矩阵因子外，QR分解是唯一的。由以上事实可知，对于双精度图像矩阵，无论是否为方阵，都可以进行QR分解。

3 图像水印方法

本节将给出水印嵌入和提取的程序。以下假设X是M× N的原始宿主灰度图像，每个像素点处的像素值为x(m,n)(1≤m,n≤M)。同样假设W是N×N的二值水印图像，且W中每个像素点处的像素值为w(i,j)(1≤i,j≤N)。

3.1 水印的嵌入

算法的具体步骤如下：

(1)将宿主图像矩阵X拉成一列向量X'M2×1，并对其元素按从小到大排序得到Y'M2×1，记录每个元素在X'中的初始位置。记为向量E。

(2)恢复向量Y'，得到一个M×M的矩阵，记为Y。

(4)分数域低频子图LLM/2×M/2划分为不重叠的N2个方块

(5)应用QR分解到上述的每一个子块得到矩阵Qij和Rij，[Qij,Rij]=qr(bij)，其中Rij是一个上三角矩阵。

(6)按照以下方法嵌入二值水印到Rij的第一行Rij(1，：)，

(8)利用LLw和步骤(3)中得到的3个分数域高频子图，进行逆LCWT得到嵌入水印后的置乱图像Yw。

(9)利用步骤(1)中记录下的位置向量E对Yw进行还原得到嵌入水印的宿主图像。

3.2 水印的提取

本小节将介绍水印提取的详细步骤，其中会使用水印嵌入中得到的向量K和嵌入水印后的置乱图像Yw，具体步骤如下：

(1)应用1级FRWT到Yw得到分数域的低频子图LL0和3个分数域高频子图。

(3)对每一个方块进行QR分解得到2个矩阵QOij和ROij。

(4)利用ROij(1，：)矩阵的第一行ROij(1，：)，按如下方式提取水印图像，

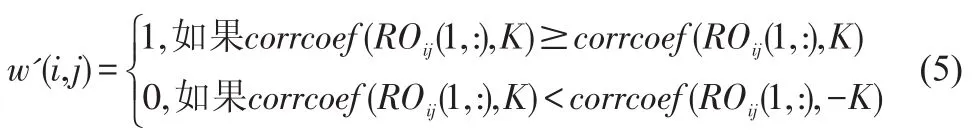
其中corrcoef(:，:)代表2个图像的标准协方差。

4 实验结果与分析

使用MATLAB-2014a软件分析水印的不可见性和鲁棒性。选用5幅大小为512×512具有不同纹理特征的标准测试图像作为原始宿主图像，如图1(a)-(e)所示。使用大小为64×64的含有字符信息“USTB”的二值图像作为嵌入的水印p=0.95。本文使用峰值信噪比(PSNR)、归一化相关(NC)和结构相似度(SSIM)三个指标从不同方面衡量本方法水印的不可见性以及鲁棒性，其中PSNR用来衡量嵌入水印的宿主图像的视觉质量，PSNR值越大，说明水印方法对图像的破坏越小，也意味着水印的不可见性越好。它的定义为：

其中f和fw分别代表大小为M×N的原始宿主图像和嵌入水印后的宿主图像。

NC和SSIM用来衡量提取出的水印与原水印的相似度，值越大说明两者的相似度越高。他们的定义为：

其中w是原始水印图像，w’是提取出的水印图像。μw和μ'w是w和w'的期望，σw和σw'是w和w'的方差，σww'是w和w'的协方差，c1和c2是两个保持除法成立的变量。

图1 原始宿主图像和水印图像

4.1 水印的不可见性

水印在通常的视觉条件下是不可见的，所以水印的存在不会影响作品的视觉效果，水印的不可见性是考察水印方法优劣的重要的一个方面。本小节从以下2个角度考虑水印的不可见性：

(1)计算嵌入水印后宿主图像的PSNR值：通常只有PSNR值大于40dB时，才能保证水印不可见性[20]；

(2)当保证嵌入水印后宿主图像具有较高的PSNR值时，是否可以准确地提取出水印图像。

基于以上考虑，嵌入水印图像到图1所示的5幅标准宿主图像，采用不同的嵌入强度λ=10-20，得到嵌入水印后宿主图像的PSNR值，为了直观地观察数值变化趋势，以λ为自变量，PSNR值为因变量绘制函数图像，如图2所示。从图2中可以得到随着λ的增大，PSNR值在减小，当λ=20时，PSNR的值小于40dB，所以只要λ＜20都可以，所以实验中选取λ=15作为嵌入强度值，得到嵌入水印的宿主图像后，计算其PSNR值。提取相应的水印列举在表1的第一行和第三行，并计算相应的NC和SSIM值，见表1。分析表1中的图像及数据，可以得到：一方面，嵌入水印后的宿主图像视觉质量很好，意味着水印的不可见性很好；另一方面，提取出的水印清晰，与原水印图像比较并未有明显误差，这说明水印提取的准确性较高。从客观数据方面，PSNR的值均高于40dB，符合要求。NC和SSIM值都为1，这说明提取出的水印与原水印相似度很高，与视觉观察得到的结果是吻合的。

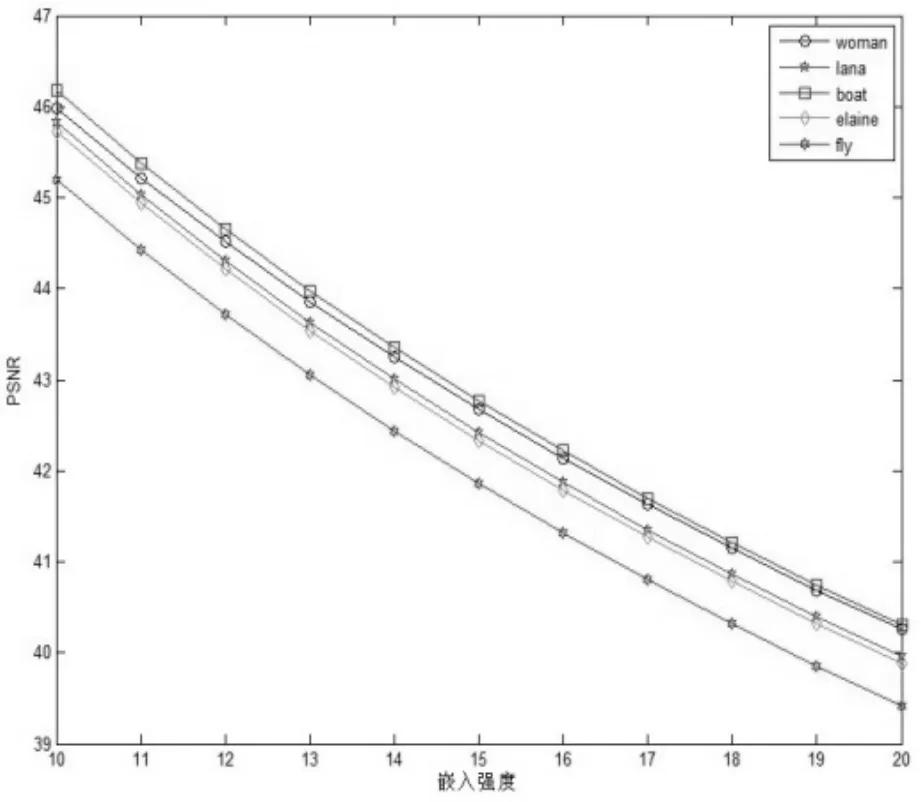
图2 基于不同测试图像得到的峰值信噪

表1 嵌入水印的5幅宿主图像以及相应提取到的水印

4.2 算法的鲁棒性

选用Lena图像作为测试图像，分别对图像进行旋转、放缩来验证算法的鲁棒性。为比较本文算法与文献[13]和[16]所提算法的性能，同样采用具有“USTB”字符意义的二值图像作为水印图像，验证不同算法2种典型攻击的鲁棒性。以下简记本文所提算法为FRWT+QR，文献[16]所提算法为QR，文献[13]所提算法为DWT+QR。

4.2.1 旋转鲁棒性

首先选取旋转的角度从0o变化到90o，以5o为间隔，分别基于3种方法提取水印，得到的水印图像分别见图3的(a)，(b)和(c)。从图3中可以看出，在旋转攻击下，3种水印方法均不能完全提取水印，但是基于本文所提出的水印方法得到的水印图像的误差仅出现于文字的四周，并不影响文字的观察，而其它2种方法的误差分布于整个图片，影响文字的观察。其次，为了更加精确地比较3种方法的性能，进一步选取其中的10幅计算提取出的水印图像与原水印图像之间的NC和SSIM值，见表2。为了直观地观察随着角度的增加NC和SSIM值的变化趋势，以旋转角度为自变量，NC和SSIM值分别为因变量绘制曲线，见图4(a)和(b)。从图4可以看出，随着旋转角度的增加，NC和SSIM值总体上具有对称性，本文所提方法NC值略高于其它2种方法，本文所提方法的旋转鲁棒性较好。

图3 旋转攻击下不同方法提取出的水印

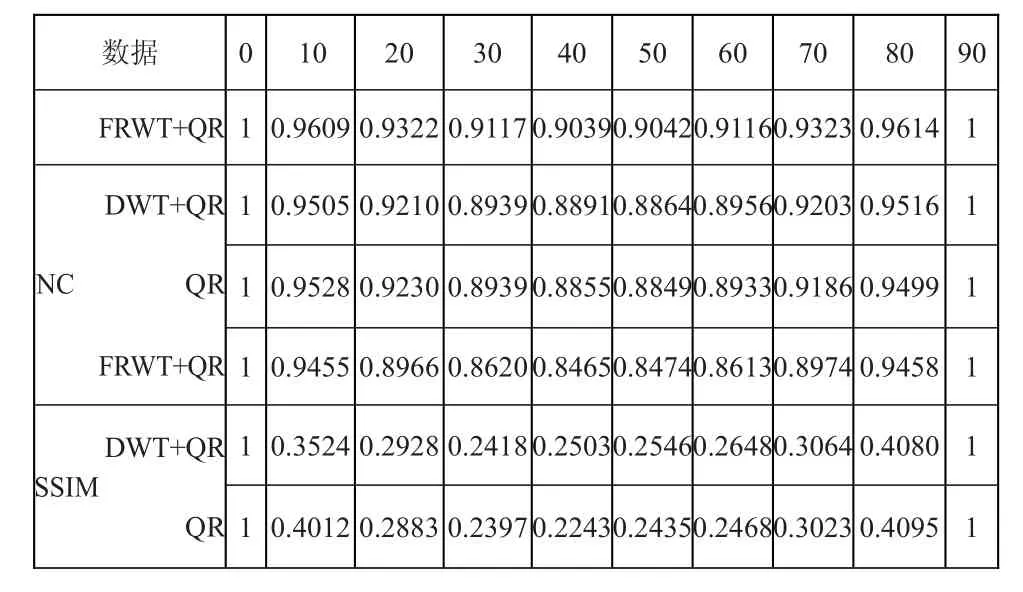
表2 旋转攻击下得到的NC和SSIM值

图4 在旋转攻击下三种不同方法的性能比较

4.2.2 放缩鲁棒性

首先选取放缩比例从0.1变化到1，以0.1为间隔，分别基于3种方法提取水印，得到的水印图像如图5所示。提取出的水印图像与原水印图像之间的NC和SSIM值，见表3。并且为了直观地观察随着放缩比例的增加NC和SSIM值的变化趋势，以放缩比例为自变量，NC和SSIM值分别为因变量绘制曲线，见图6(a)和(b)。从图5可以看出，在放缩攻击下，当放缩比例大于0.2时，基于本文所提方法提取到的水印清晰可见，而基于其它2种方法得到的水印模糊，无法辨认水印内容。从图6和表3中可以得到，随着放缩比例的变大，NC和SSIM值总体上在变大，当放缩比例为1时，也就是说没有攻击时，达到最高值1。本文所提方法NC和SSIM值上升的速度更快，而其它2种方法上升速度缓慢且每一个值均低于本文所提方法。综合以上分析，相比于其它2种方法，本文所提方法的放缩鲁棒性更好。

图5 放缩攻击下不同方法提取出的水印

表3 缩放攻击下得到的NC和SSIM值

图6 缩放攻击下三种不同方法的性能比较

5 结论

由于FRWT具有的FRFT域多分辨表示图像的能力，本文提出一种基于FRWT和QR分解的新颖数字图像水印方法。实验结果表明，嵌入水印后的宿主图像的PSNR值均高于40dB，说明该方法具有良好的水印不可见性，并且当嵌入水印的宿主图像遭到不同类型的攻击时，仍然可以快速有效地提取到清晰的水印图像，综合以上分析可知本方法很好地平衡了水印的不可见性和鲁棒性，尤其对于几何攻击如旋转和放缩具有较好的鲁棒性。

[1]Al-Asmari A K，Salama A，Iliyasu A M，et al．A DWT ordering scheme for hiding data in images using pixel value difference[C]Computational Intelligence and Security(CIS)，2012 Eighth International Conference on．IEEE，2012：553-557．

[2]Lang J，Zhang Z．Blind digital watermarking method in the fractional Fourier transform domain[J]．Optics and Lasers in Engineering，2014，53：112-121．

[3]许天周，李炳照．线性正则变换及其应用[M]．北京：科学出版社，2013．

[4]陶然，邓兵，王越．分数阶傅里叶变换及其应用[M]．北京：清华大学出版社，2009．

[5]Qi M，Li B Z，Sun H．Image watermarking via fractional polar harmonic transforms[J]．Journal of Electronic Imaging，2015，24(1)：013004-013004．

[6]Qi M，Li B Z，Sun H．Image watermarking using polar harmonic transform with parameters in SL(2，R)[J]．Signal Processing：Image Communication，2015，31：161-173．

[7]Singh A K，Dave M，Mohan A．Hybrid Technique for Robust and Imperceptible Image Watermarking in DWT-DCT-SVD Domain[J]．National Academy Science Letters，2014，37(4)：351-358．

[8]Sirmour S，Tiwari A．A Hybrid DWT-SVD Based Digital Image Watermarking Algorithm for Copyright Protection[J]．International Journal of p2p Network Trends and Technology，2014，6．

[9]Ali M，Ahn C W．An optimized watermarking technique based on self-adaptive DE in DWT-SVD transform domain[J]．Signal Processing，2014，94：545-556．

[10]Mishra A，Agarwal C，Sharma A，et al．Optimized gray-scale image watermarking using DWT-SVD and Firefly Algorithm[J]．Expert Systems with Applications，2014，41(17)：7858-7867．

[11]Y．Naderahmadian，S．Hosseini-Khayat，“Fast watermarking based on QR decomposition in Wavelet domain”．Intelligent Information Hiding and Multimedia Signal Processing(IIH-MSP)，2010 Sixth International Con-ference on．IEEE，127-130(2010)．

[12]Rajab L，Al-Khatib T，Al Haj A．A Blind DWT-SCHUR Based Digital Video Watermarking Technique[J]．Journal of Software Engineering and Applications，2015，8(04)：224．

[13]Jane O，Elbasi E．A new approach of nonblind watermarking methods based on DWT and SVD via LU decomposition[J]．Turkish Journal of Electrical Engineering Computer Sciences，2014，22(5)．

[14]Naderahmadian Y，Hosseini-Khayat S．Fast and robust watermarking in still images based on QR decompo-sition[J]．Multimedia Tools and Applications，2014，72(3)：2597-2618．

[15]史军，张乃通，刘晓萍．一种新型分数阶小波变换及其应用[J]．中国科学：信息科学，2012，42(2)：125-135．

[16]Shi J，Liu X，Zhang N．Multiresolution analysis and orthogonal wavelets associated with fractional wavelet transform[J]．Signal，Image and Video Processing，2013，9(1)：211-220．

[17]徐小军，王友仁，陈帅．基于下采样分数阶小波变换的图像融合新方法[J]．仪器仪表学报，2014，35(9)：2061-2069．

Blind Digital WatermarkingAlgorithm Based on FRWT and QR Decomposition

Li Qian Zhuo ZhihaiWang Yuduo
(Beijing Information Science and Technology University,Beijing 100101)

This paper presents a novel method based on the blind digital image watermarking methods of FRWT and QR decomposition.Compared with the existing DWT domain digital image watermarking method,this method combines the advantages of both FRWT and DWT,which has better flexibility.The simulation results show that the PSNR value of the host image embedded with the watermark is higher than 40dB,which fully demonstrates that the algorithm can not only balance the imperceptibility of the watermark,but also has better robustness against geometric attacks.

digital image watermarking;Fractional Wavelet Transform(FRWT);Fractional Fourier Transform;QR decomposition

TP391

B

1008-6609(2017)07-0001-06

李茜（1991-），女，河北保定人，硕士，研究方向为数据采集与信号处理、分数域小波变换。

北京市支持中央在京高校共建项目，项目编号：504160214；北京信息科技大学校基金，项目编号：1425011；北京信息科技大学2016年度教学改革立项资助，项目编号：2016KGYB20。