时间序列分段加权的引水量预测方法

王建兴

（山东省莱州水务局，山东 烟台 261400）

时间序列分段加权的引水量预测方法

王建兴

（山东省莱州水务局，山东 烟台 261400）

结合新疆某水库，对引水量的线性预测模型与二次预测模型进行校验，证明了其可用性。通过建立的分段加权预测方法，得到了该案例中2017年的引水量的考虑数据量和考虑数据远近的预测值。

引水量；时间序列；线性预测；二次曲线预测；水库；分段加权

水量的预测研究，国内外学者已经进行了大量工作，诸如MODFLOW模拟方法［1］、小波分析理论［2］、支持向量回归［3］、改进GM（1，1）模型［4］、加权马尔可夫链［5］等，但经作者对比，这些方法非常繁琐，需要具有强大数学理论作为支撑，而目前，较为缺乏简单易算的适用于工程上的预测方法，鉴于此，该文基于时间序列法对水库的引水量进行预测研究，旨在构建一种工程上适用的简单易算的预测模型。

1 时间序列预测法的基本原理

作为定量预测方法之一，时间序列法在统计学中广泛被用到预测领域。其原理为通过对预测数据所对应的历史时间数据进行分析，并建立历史时间数据与目标的对应函数关系，通过历史时间与历史目标数据的变化规律，对下一时刻进行目标预测。

时间序列法的核心为时间历史数据，即把预测对象及其相关的影响因素都看成和时间历史有关的函数规律，以此对目标进行变化规律与发展趋势的时序研究，同时，时间序列法还有另外一种预测方法，该方法通过预测目标与其影响因素之间的影响程度的函数关系来进行相关预测，而由于预测目标所对应的影响因素甚多，一般仅仅选择与预测目标相关性较大的因素作为考虑因素，即为少因素分析原理。

2 预测方法和模型

预测模型的选择决定着预测的准确性，而影响水库水量的因素较为复杂，难以建立相关分析模型，且各类影响因素历史数据信息难以搜集到。鉴于此，基于少因素分析原理，该文引水量的预测，暂不考虑影响因素的关系，而是根据水库历年来引水量的历史时间数据进行时间序列分析，并对其变化规律进行分析。现以一次线性拟合预测和二次曲线拟合预测为例对模型的预测方法进行阐述。

2.1 线性拟合模型

对线性拟合的模型方程进行建立，则有：

式中 t为年份，t=t0+n；t0为起始年份；n为起始年份后的年份；A为斜率系数；B为截距系数。

系数A和B通过最小二乘法的拟合可以求得，其原理为，根据数据进行线性拟合，拟合的数据与实际值所得的离差平方和最小，所得的系数即为A和B，借助于EXCEL的函数功能求得式（2）和式（3）：

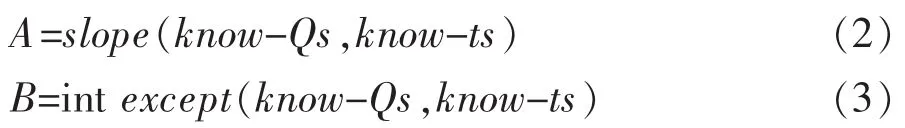
式中 know-Qs为水库所对应的引水量；know-ts为水库所对应的时间序列。

2.2 二次曲线预测模型

对二次曲线预测模型方程进行建立，如式（4）。

由式 （4）可以得出二次曲线模型的方程式，其中，a，b，c为拟合系数。

式中 Know-Qs为水库引水量数值；Know-ts为水库引水量所对应的时间序列。

3 时间序列加权分段预测模型

从实际引水量调度发现，引水量随时间往往并不是完全符合单个预测模型，例如引水量并非在整个时域内完全符合线性模型或二次曲线模型，其往往是在某个时间子域内符合线性模型，而在另一个时间子域内符合二次曲线模型，引水量随时间的分布具有分段函数的性质，当然，这种分段子函数除了线性函数与二次函数外，还有可能存在诸如三次函数、四次函数等复杂子函数，但一般地，线性函数和二次函数，可以较好地表述这种性质，因此该文重点以一次函数和二次函数作为分段子函数进行研究，并基于此建立时间序列加权分段预测模型。

加权分段预测模型的核心在于充分考虑时间序列所包括的数据信息，将以为所有数据信息点均作为预测的基础之一，基于此，构建两种分段加权预测模型，一种为考虑数据点的量为加权预测的基础，另一种为考虑数据点所对应的时间段离当前需要预测时刻的远近作为加权预测的基础。

3.1 考虑数据点量的加权预测

引水量数据点的数据量反映的是其处于这种数据模式下所占的时间周期长短，时间周期长的分段数据函数应具有较大的权重，而时间周期短的分段数据函数应具有较小的权重，基于该原则，所构建的分段加权时间序列模型如式（8）。

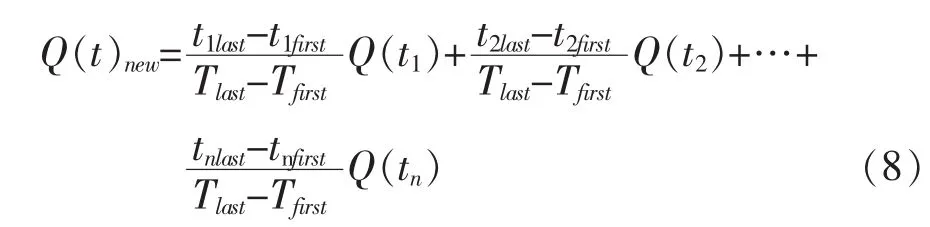
式中 Q（t）new为新的引水量预测数据值；Q（t1）为所在第一子域的引水量预测函数 （线性函数或者二次函数）；Tfirst为整体时域的初始时间点；Tlast为整体时域的末尾时间点；tnfirst为第n个分段子域的初始时间点；tnlast为第n个分段子域的末尾时间点，且时间点符合式（9）。

基于式（8），式（9）便可进行未来时域（未知时域）引水量Q（t）new的预测，此为考虑数据点量的时间序列分段加权预测方法，其权即为

3.2 考虑数据点远近的加权预测

引水量数据点离期望预测时域数据点远近的不同反映出历史数据对期望预测时域影响程度的不同，一般来说，离期望预测时域预测点越远的数据，其影响程度越小，相应的对应的权重也应该越小，而离期望预测时域预测点越近的数据，其影响程度越大，相应的对应的权重也应该越大，基于该原则，所构建的分段加权时间序列模型如式（8）：

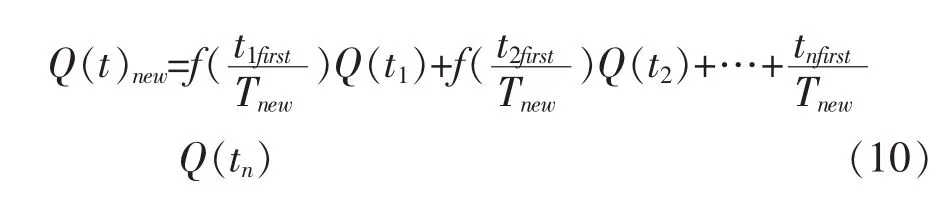
式中 Tnew为所期望的预测时间点为第n个分段子域的起始时间点与期望预测时间点比值的归一化数值。

基于式（10）便可进行未来时域（未知时域）引水量Q（t）new的预测，此为考虑数据点远近的时间序列分段加权预测方法，其权即为

4 案例

4.1 引水量时间序列

某水库位于新疆莎车县依盖尔其镇，水库设计库容6200万m3，现状实测库容4758万m3。该水库1996～2016年的引水量如表1，现需要对其2017年的引水量进行预测。

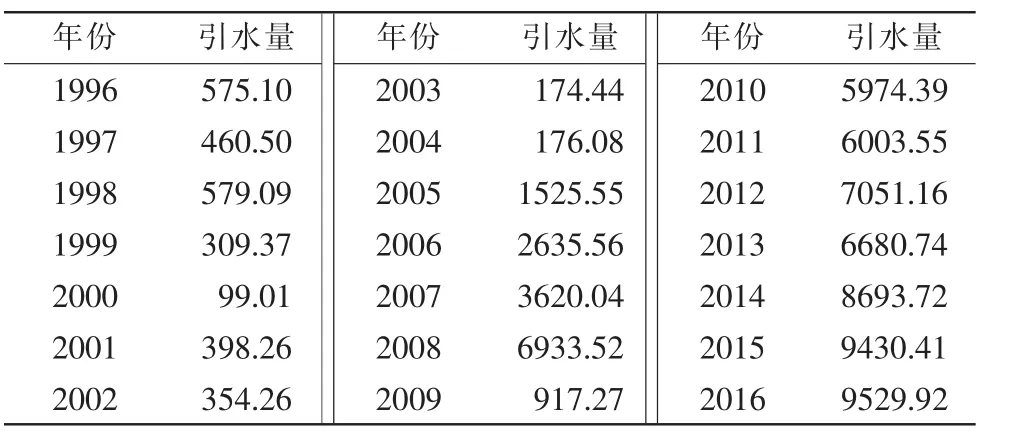
表1 某水库引水量 单位：万m3

由表1所得数据，绘出该水库引水量随时间的变化曲线规律，如图1。

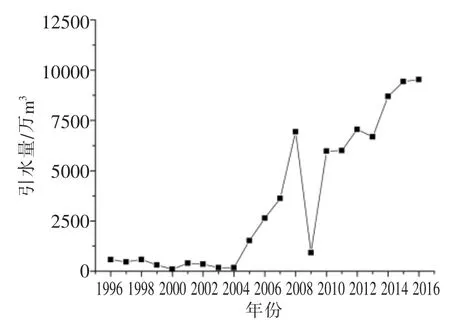
图1 水库引水量随时间变化曲线

4.2 数据预测建模与预测检验

基于上述分析，采用分段方法来进行时间序列，对1996～2004年建立线性时间序列拟合趋势模型，对2004～2008年，亦采用线性拟合时间序列模型，而对2009～2016年，采用二次时间序列拟合模型，以此，用一个确定的时间序列函数Q（t）来进行时间序列的拟合。

根据式（1）～式（3），可得1996～2004年的引水量线性预测模型为式（11）；2004～2008年的引水量线性预测模型为式（12）；2009～2016年的引水量线性预测模型为式（13）。

分别将所对应的时间序列数据代入式 （11）～式（13），便可得出预测数据值，如图2和图3。

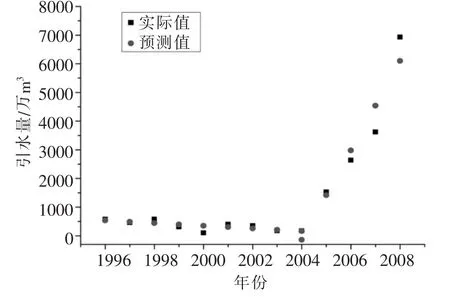
图2 实际值与预测值对比

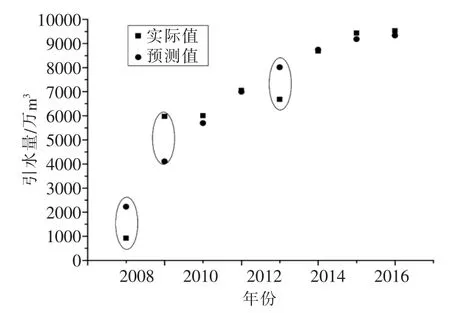
图3 实际值与预测值对比

从图2可以看出，线性预测所得的实际值和预测值几乎相当，数据差距不大，而1996～2004年的预测结果明显要优于2004～2008年的预测结果，同时，2004年由前后两种预测模型预测，前段预测效果优于后段，在此，2004年的预测值取前段预测值。

由图3可知，二次曲线预测模型预测结果与实际值在总体上具有吻合性，但在2009，2010，2013年存在一定预测误差，如图3中黑色圈划部分，而其他年份的预测结果具有高度吻合性，几乎完全重合，以此说明二次预测模型基本能够揭示出2009～2016年的水库引水量变化规律。

由图2和图3可知，基于时间序列的原理，针对水库的引水量建立了线性预测模型和二次曲线预测模型，两种模型的预测值与实际值总体上大致相当，具有一定的吻合性，说明预测模型具有适用性。

4.3 时间序列的分段加权预测

根据建立的预测模型，对2017年的引水量进行预测，首先进行考虑数据量的分段加权预测，Q（t）1996～2004，Q（t）2004～2008，Q（t）2009～2016分别为Q（t1），Q（t2），Q（t3），将其与时间序列值代入式（8）得：

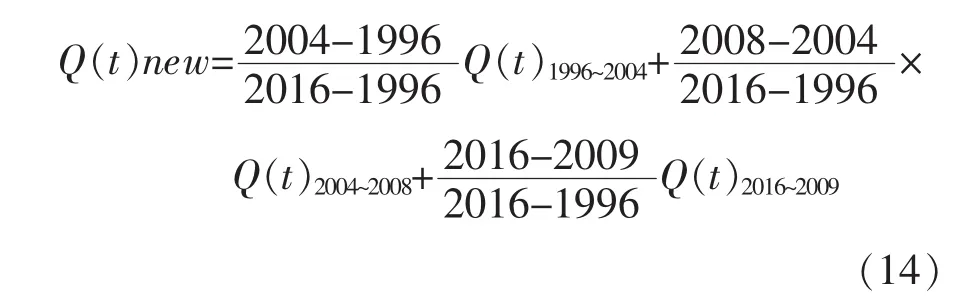
经计算，2017年水库预测值7068.17万m3，该数据为考虑数据点量的分段加权预测方法。

同理，将Q（t）1996～2004，Q（t）2004～2008，Q（t）2009～2016分别代入式（10）的Q（t1），Q（t2），Q（t3），并将时间序列代入式（10），可得虑数数据点远近的2017年的加权数据预测值6892.35万m3。

考虑数据点量的分段加权预测值和考虑数据点远近的分段加权预测值分别为9191.271万m3和6892.35万m3，两种方法的预测结果具有一定差距，但却有可取之处，前者是充分考虑历史数据进行预测，而后者是更加侧重于近期的数据进行预测，因此，两种方法从不能角度得出了相应的预测值。使用者可以通过对两种方法取平均值，作为最终的预测结果。

5 结语

（1）基于时间序列的原理，以线性预测模型和二次曲线预测模型为基础，建立了两种引水量的分段全权时间序列预测方法，即为考虑数据量的分段加权预测方法和考虑数据点远近的分段加权预测方法。

（2）基于所建立的预测模型，进行了线性预测模型和二次预测模型的拟合与校验，校验合理后，采用考虑数据量和考虑数据远近方法对2017年的水库引水量进行预测，得出了相应的预测值，均具有一定的说服力。

［1］周冬林，许模，万廷剑.MODFLOW模拟预测不同施工方式隧洞涌水量的差异［J］.甘肃水利水电技术，2015，51（1）：27-30.

［2］曹庆奎，赵斐.基于遗传-支持向量回归的煤层底板突水量预测研究［J］.煤炭学报，2011，36（12）：2097-2101.

［3］佟长福，史海滨，包小庆，等.基于小波分析理论组合模型的农业需水量预测［J］.农业工程学报，2011，27（5）：93-98.

［4］王桂智，唐德善.改进GM（1，1）模型在台兰河灌区引水量预测中的应用［J］.水利科技与经济，2012，18（2）：28-30.

［5］董起广，韩霁昌，张卫华，等.基于加权马尔可夫链的延安市降水量预测［J］.人民珠江，2015（5）：64-67.

（责任编辑：王艳肖）

W ater diversion quantity forecastingmethod based on piecew ise weighting time seriesmode

WANG Jian-xing
（Laizhou Water Suthority，Yantai261400，China）

Combined with a case，the linear prediction model and the quadratic curve prediction model of the reservoir water diversion quantity are verified，which proves their availability.Based on the establishment of piecewise weighted predictionmethod，the water diversion quantity in 2017 is obtained in two perspectives.

water diversion quantity；time series；linear prediction；quadratic curve prediction；reservoir；subsection weight

TV122

：B

：1672-9900（2017）04-0032-04

2017-06-12

王建兴（1963-），男（汉族），山东莱州人，工程师，主要从事水利工程管理等工作，（Tel）13589775667。