前驱体浸渍法制备泡沫镍屈服强度与孔结构的关系

2017-09-06王辉向长淑王建李广忠周进雄

粉末冶金材料科学与工程 2017年4期

王辉，向长淑，王建，李广忠，周进雄

(1. 西北有色金属研究院金属多孔材料国家重点实验室，西安 710016；2. 西安赛隆金属材料有限责任公司，西安 710016；3. 西安交通大学机械结构强度与振动国家重点实验室，西安 710049)

王辉1,2，向长淑2，王建1，李广忠1，周进雄3

采用有限元模拟技术计算不同孔结构泡沫镍的屈服强度，并以气雾化Ni-20Cr合金粉末为原料，以不同孔径的聚氨酯泡沫为模板，控制浸渍工艺制备出不同孔径与不同密度的泡沫镍铬合金，研究合金屈服强度随密度与孔径尺寸的变化关系。有限元模拟计算结果表明，开孔泡沫金属材料的屈服强度符合Gibson-Ashby方程，在开孔泡沫金属材料密度一定的情况下，材料的屈服强度不随孔径的变化而变化。实验结果表明，对于相同孔径的泡沫金属材料，其屈服强度和相对密度的关系为σ/σs与相对密对(即ρ/ρs)的1.5次方呈线性关系(σ和σs分别为泡沫材料与致密材料的屈服强度；ρ和ρs分别为泡沫材料与致密材料的密度)；而具有相同密度和不同孔径的泡沫镍铬合金，其屈服强度很接近，验证了开孔泡沫金属材料屈服强度随密度的变化规律符合Gibson-Ashby方程。

泡沫镍；有限元模拟；前驱体浸渍法；孔结构；屈服强度

泡沫金属材料具有低密度、高比强度、优良的能量吸收率等特点、以及结构和功能的双重特性，其应用涉及过滤、分离、吸能、降噪、屏蔽、催化和热交换等多个方面[1−3]。泡沫镍基合金被认为是继泡沫镍之后更具应用价值的泡沫结构工程材料。在泡沫镍中添加铬元素，可有提高基体强度尤其是高温持久强度，同时氧化和腐蚀过程中合金表面形成致密的Cr2O3膜，可有效提高合金的抗氧化性能和耐蚀性能。因此，泡沫镍铬合金在催化剂载体、过滤器、燃料电池电极和热交换器等领域具有广阔的应用前景[4−6]。前躯体浸渍法以聚氨酯泡沫作为模板(前躯体)，工艺简单且孔径易于调控，适于制备高孔隙率材料，特别是制备具有连通孔结构的开孔泡沫材料，目前已广泛应用于高孔隙率泡沫陶瓷等泡沫材料的制备[7−8]。多年来，研究者们在多孔材料的结构与性能方面取得了大量的研究成果。其中，由Gibson和Ashby等创建的Gibson-Ashby模型和相关理论，是多孔材料领域公认的经典模型理论，在国内外同行的研究中得到广泛应用[9−10]。在该模型的分析基础上，Gibson和Ashby得到了开孔泡沫材料屈服强度的表达式，即Gibson-Ashby方程[9]：σ/σs≈C(ρ/ρs)1.5。式中，σ和ρ分别为开孔泡沫材料的屈服强度和表观密度；σs和ρs分别为相同材质的致密材料的屈服强度和密度；C为常数。从该方程中发现，在材料一定的前提下，开孔泡沫材料的屈服强度只与其相对密度(孔隙度)有关，与孔形状、孔径尺寸、孔筋尺寸等因素无关。根据对称操作，Gibson-Ashby模型的孔隙单元和结构单元均实现了结构均匀和三维各向同性，但这种立方结构孔隙单元的集合体不能很好地反映出以开孔聚氨酯泡沫为模板制备的泡沫金属材料的3根孔筋(棱柱)相交于一个节点叠加连接形成的类金刚石集合体结构。因此，对于前驱体法制备的泡沫金属材料而言，有必要选取新的单胞模型进行模拟计算，并制备不同孔结构的泡沫材料进行验证。本文作者采用有限元法，结合Abaqus软件建立模型，通过数据分析；研究相同密度泡沫镍的屈服强度与孔径尺寸的关系；并以不同孔径的聚氨酯泡沫为前驱体，以气雾化Ni-20Cr粉末为原料配制水基浆料，采用浸渍法制备不同密度的泡沫镍铬合金，测试泡沫镍铬合金的屈服强度，此基础上验证Gibson-Ashby方程，并对泡沫镍铬合金的实际应用提供数据支持。

1 实验

1.1 有限元模拟

根据实际聚氨酯泡沫前驱体的结构特性，采用图1(a)所示的金刚石结构，按照该结构建模的单个胞元如图1(b)所示。将纯镍的材料参数(弹性模量为E=214 GPa，屈服强度为105 MPa)导入Abaqus软件进行其轴向压缩受力情况的有限元分析，为了较好地反映泡沫材料受压的实际情况，同时考虑到合适的数据处理量，选取8个连续胞元组成的模型并施加边界条件，模型及压缩受力方式如图1(c)所示。

图1 聚氨酯泡沫的Abaqus计算模型Fig.1 Abaqus calculation model of PU foam (a) Diamond cubic crystal structure; (b) Single cell-element; (c) Calculation model and stress characteristics

1.2 合金制备及性能测试

采用平均粒径为20 μm的气雾化Ni-20Cr合金粉末(粉末形貌如图2所示)为原料，分别以孔径为10，20，30和40 PPI(par per inch，每英寸上的孔数量)的聚氨酯泡沫为模板，添加5%(质量分数)的聚乙烯醇(PVA)作为粘结剂，加入0.6%(质量分数)的羧甲基纤维素(CMC)作为流变调节剂，用去离子水配制成浆料，浆料的固含量为70%。通过控制浸渍道次和辊压压力等参数得到不同密度的泡沫合金素坯。素坯经低温预烧+高温烧结的两步烧结后，得到泡沫镍铬合金[11]。

图2 Ni-20Cr合金粉末的SEM形貌Fig.2 SEM Morphology of the Ni-20Cr alloy powder

用线切割将泡沫镍铬合金加工成直径20 mm、长度为10 mm的圆柱试样[12]，按照国标GB/T 6343—2009泡沫塑料表观密度测定方法测定合金的密度，并计算相对密度；用Instron−3343型力学性能试验机进行室温压缩性能测试，得到应力–应变曲线，压头的压下速率为0.5mm/min。

2 结果与讨论

2.1 有限元模拟结果

对于已选定的泡沫材料模型，可通过改变如图3所示的棱柱的几何尺寸来改变泡沫金属材料的孔结构(主要是孔径的改变)和密度，也就是通过改变棱柱的长度L来改变泡沫金属材料的孔径，通过改变棱柱截面尺寸t来改变材料的密度。对于图1(c)所示模型而言，相对密度ρ正比于横截面边长t与棱长L之比的平方，即(ρ/ρs)∝(t/L)2，同时改变边长t和棱长L使t/L的值不变，即可保证泡沫体密度相同。本次计算选取5组数据进行有限元分析：t=0.2mm，L=2mm；t=0.3mm，L=3mm；t=0.4mm，L=4mm；t=0.5mm，L=5mm；t=0.6 mm，L=6 mm，泡沫镍的相对密度为1.3%。图4所示为5组具有相同密度(t/L的值相同，均为0.1)和不同孔径的泡沫镍的压缩应力−应变曲线。从图中可看出，在相对密度相同的情况下，不同孔径泡沫镍的应力−应变曲线较接近。将5组曲线对应的泡沫镍的屈服强度列于表1，从表1看出，在泡沫体密度相同的前提下，改变泡沫金属材料的孔径，材料的屈服强度变化不大。这表明开孔泡沫金属材料的屈服强度符合Gibson-Ashby方程中的规律，即在开孔泡沫金属材料密度一定的情况下，材料的屈服强度不随孔径尺寸变化而变化。这个结果与Nieh对开孔泡沫铝屈服强度的研究结果一致[13]。

图3 计算模型胞元中的棱柱Fig.3 Sing prism in simulation model

图4 相同密度、不同孔径泡沫镍的压缩应力–应变曲线Fig.4 Stress–strain curve of nickel foam with same density but different pore sizes

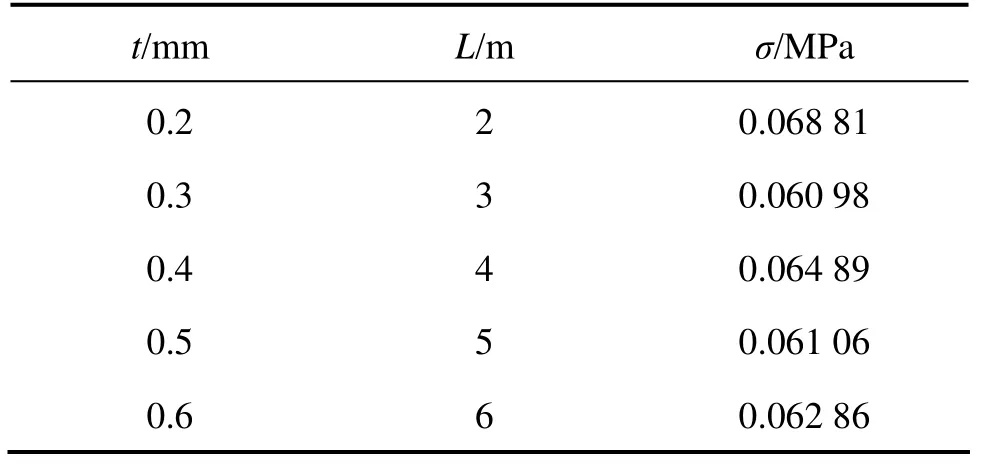
表1 相对密度同为1.3%，不同孔结构泡沫镍的屈服强度Table 1 Yield strength of Nickel foam with same relative density of 1.3% but different pore structure

2.2 实验结果

采用孔径为20 PPI的聚氨酯泡沫，通过控制浸渍工艺制备2种不同密度的泡沫镍铬合金，分别编号为NiCr-20−1和NiCr-20−3，通过测试和计算，这2种合金的相对密度分别为7.5%和9.5%，其室温压缩的应力−应变曲线如图5所示。从图5得到NiCr-20−1和NiCr-20−3的屈服强度σ分别为3.30 MPa和4.43 MPa，将各数据代入Gibson-Ashby方程，得到NiCr-20−1和NiCr-20−3的材料参数C分别为0.247和0.232(见表2)，较为接近。

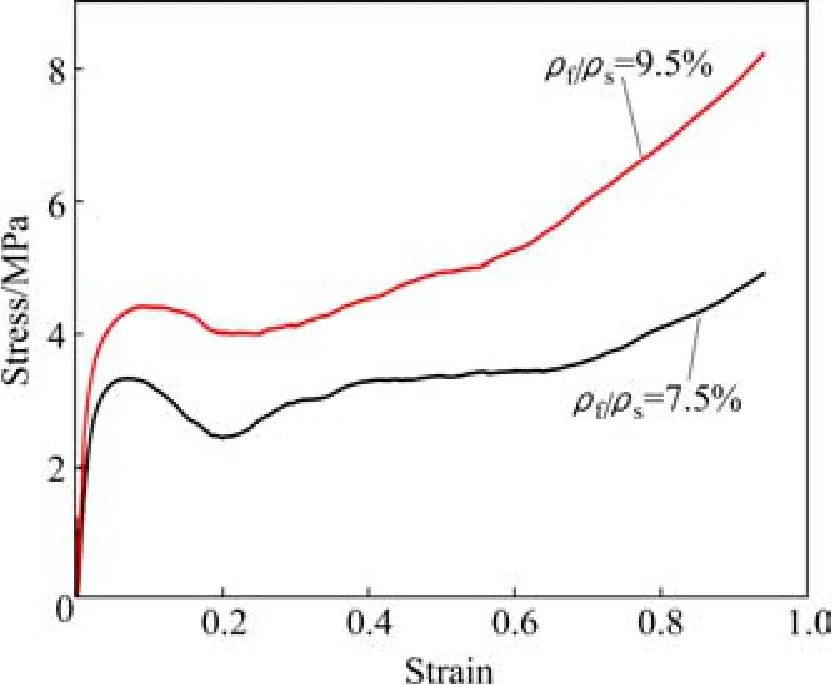
图5 相同孔径、不同密度泡沫镍铬合金的压缩应力−应变曲线Fig.5 Stress-strain curve of nickel-chromium alloy foam with same pore size but different density

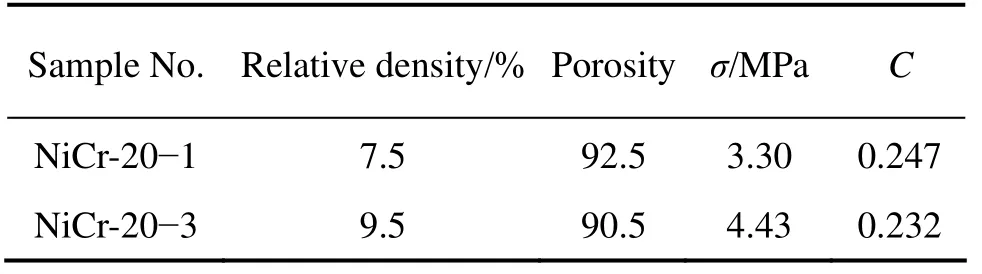
表2 相同孔径、不同密度泡沫镍铬合金的屈服强度与材料参数CTable 2 Yield strength of nickel-chromium alloy foam with same pore size but different density

采用孔径分别为10，30和40 PPI的聚氨酯泡沫，通过控制浸渍工艺制备不同孔径和不同密度的泡沫镍铬合金，测定其屈服强度，再将具有相同孔径的合金的屈服强度与相对密度的关系进行拟合，如图6所示。由图可见，对于相同孔径的泡沫镍铬合金而言，其屈服强度和相对密度的关系基本符合Gibson-Ashby方程，即σ/σs与ρ/ρs的1.5次方呈线性关系；而具有相同密度和不同孔径的泡沫镍铬合金，其屈服强度很接近。这与数值模拟结果一致，验证了开孔泡沫金属材料的屈服强度符合Gibson-Ashby方程的变化规律，即开孔泡沫金属材料的屈服强度随材料密度的变化而变化，与材料孔结构没有必然联系。

图6 不同孔径的泡沫镍铬合金屈服强度与相对密度的关系Fig.6 Relationship between yield strength and relative density of nickel-chromium alloy foam with different pore size

3 结论

1) 利用Abaqus软件对金刚石结构的开孔泡沫镍铬合金进行有限元计算分析，计算结果表明，开孔泡沫金属材料的屈服强度符合Gibson-Ashby方程，即在开孔泡沫金属材料密度一定的情况下，材料屈服强度不随孔径尺寸的变化而变化。

2) 实验结果表明，对于相同孔径的泡沫镍铬合金而言，其屈服强度和相对密度的关系符合Gibson-Ashby方程，σ/σs与ρ/ρs的1.5次方呈线性关系；而具有相同密度和不同孔径的泡沫镍铬合金，其屈服强度很接近，验证了开孔泡沫金属材料屈服强度随密度的变化符合Gibson-Ashby方程。

REFERENCES

[1] BOONYONGMANEERAT Y, SCHUH C A, DUNAND D C. Mechanical properties of reticulated aluminum foams with electrodeposited Ni-W coatings[J]. Scripta Materialia, 2008, 2008, 59(3): 336−339.

[2] 段志明, 江垚, 吝楠, 等. 电镀工艺参数对泡沫镍抗拉强度的影响[J]. 粉末冶金材料科学与工程, 2009, 14(6): 432−436. DUAN Zhiming, JIANG Yao, LIN Nan, et al. Influence of plating technic parameters on tensile strength of nickel foam[J]. Materials Science and Engineering of Powder Metallurgy, 2009, 14(6): 432−436.

[3] 李瑞迪, 周科朝, 袁铁锤, 等. 泡沫镍基Ni-S-Co涂层电沉积制备工艺[J]. 粉末冶金材料科学与工程, 2006, 11(6): 349−353. LI Ruidi, ZHOU Kechao, YUAN Tiechui, et al. Electrode position technology for preparing foamy nickel matrix Ni-S-Co coatings[J]. Materials Science and Engineering of Powder Metallurgy, 2006, 11(6): 349−353.

[4] PESTRYAKOV A N, YURCHENKO E N, FEOFILOV A E. Foam-metal catalysts for purification of waste gases and neutralization of automotive emissions[J]. Catalysis Today, 1996, 29(1/4): 67−70.

[5] ATUL K, RAMANA G R. Materials and design development for bipolar/end plates in fuel cells[J]. Journal of Power Sources, 2004, 129(1): 62−67.

[6] ISMAGILOV Z R, PUSHKAREV V V, PODYACHEVA O Y, et al. A catalytic heat-exchanging tubular reactor for combining of high temperature exothermic and endothermic reactions[J]. Chemical Engineering Journal, 2001, 82(1/3): 355−360.

[7] ZHU X W, JIANG D L, TAN S H, et al. Preparation of silicon carbide reticulated porous ceramics[J]. Materials Science and Engineering A, 2002, 323(1/2): 232−238.

[8] 王军, 李靖, 杨海林, 等. 泡沫浸渍法制备小梁金属及性能[J].中南大学学报: 自然科学版, 2012, 43(5): 1684−1689. WANG Jun, LI Jing, YANG Hailin, et al. Fabrication of trabecular metal via impregtion and its properties[J]. Journal of Central South University: Science and Technology, 2012, 43(5): 1684−1689.

[9] GIBSON L J, ASHBY M F. Cellular Solids, Structure and Properties[M]. Cambridge U K: Cambridge University Press, 1997: 487−488

[10] 刘培生. 泡沫金属的经典性模型——Gibson-Ashby模型浅析[J]. 有色金属, 2005, 52(2): 55−57. LIU Peisheng. Basic analysis to classical model for foamed metals[J]. Nonferrous Metals, 2005, 52(2): 55−57.

[11] 王辉, 汤慧萍, 向长淑, 等. 梯度孔结构泡沫镍铬合金滤管的制备及性能[J]. 稀有金属材料与工程, 2014, 43(11): 2796−2800. WANG Hui, TANG Huiping, XIANG Changshu, et al. Preparation and performance of Ni-20Cr foam filter with gradient pore structure[J]. Rare Metal Materials and Engineering, 2014, 43(11): 2796−2800.

[12] ANG Q, WU G H, XIU A Y, et al. Synthesis and mechanical properties of open-cell Ni-Fe-Cr foams[J]. Materials Science and Engineering A, 2012, 534: 699−706.

[13] NIEH T G, HIGASHIB K, WADSWORTHA J. Effect of cell morphology on the compressive properties of open-cell aluminum foams[J]. Materials Science and Engineering A, 2000, 283(1/2): 105−110.

(编辑汤金芝)

Relationship between yield strength and pore structure of nickel foam prepared by impregnation method

WANG Hui1,2, XIANG Changshu2, WANG Jian1, LI Guangzhong1, ZHOU Jinxiong3
(1. State Key Lab of Porous Metal Materials, Northwest Institute for Non-ferrous Metal Research, Xi’an 710016, China; 2. Xi’an Sailong Metal Materials Co., Ltd, Xi’an 710016, China; 3. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

The yield strength of nickel foam with different pore structure were calculated by using finite element simulation. Nickel alloy foams with different density were prepared using polyurethane foam as precursor through controlling impregnation process. Relationship between pore size and yield strength of nickel chromium alloy foam was then studied. The simulation results show that the yield strength of open cell metal foam is in accordance with the Gibson-Ashby equation. That is, the yield strength of metal foam does not change with the pore size while the density of the foam material is constant. The experimental results show that for the metal foam with the same pore structure, the relationship between the yield strength and the relative density accords with Gibson-Ashby equation. And for nickel chromium alloy foam with same density and different pore size, the yield strength are very close to each other, which further verifies Gibson-Ashby equation.

nickel foam; finite element simulation; impregnation method; pore structure; yield strength

TG146

1673-0224(2017)04-585-05

国家高技术研究发展计划(863计划)资助项目(2015AA034304)；陕西省科技新星项目(2015KJXX78)

2016−12−30；

2017−04−12

王辉，工程师，博士研究生。电话：029-86232183；E-mail: wanghuicsu2008@163.com