基于有限元法的振动时效数值模拟与分析

付建科 徐 亮 雷小平 金 俊

(1. 三峡大学 机械与动力学院， 湖北 宜昌 443002； 2. 国网河南省电力公司电力科学研究院， 郑州 450052； 3. 中国电建集团 贵阳勘测设计研究院有限公司， 贵阳 550081； 4. 长江三峡通航管理局， 湖北 宜昌 443002)

基于有限元法的振动时效数值模拟与分析

付建科1徐 亮2雷小平3金 俊4

(1. 三峡大学 机械与动力学院， 湖北 宜昌 443002； 2. 国网河南省电力公司电力科学研究院， 郑州 450052； 3. 中国电建集团 贵阳勘测设计研究院有限公司， 贵阳 550081； 4. 长江三峡通航管理局， 湖北 宜昌 443002)

利用有限元分析软件ANSYS，模拟了圆管对接焊件的焊接过程，得到了焊件的残余应力场，在合理确定了振动时效工艺参数基础上，对焊件扭转振动方式的振动时效过程进行了数值模拟，分析和探讨了扭转振动方式的振动时效对消除残余应力效果的影响．模拟结果表明：在合理的振动时效工艺参数条件下，扭转振动方式的振动时效能有效减小和均化残余应力，残余应力的减小和均化效果随激振力的增大而增大．

残余应力； 扭转振动； 振动时效； 有限元法； 数值模拟

振动时效(简称VSR)是继自然时效和热时效之后发展起来的消除残余应力的方法，其基本思想是通过对工件施以交变循环载荷，使工件内残余应力得到降低或均化，从而使工件尺寸稳定下来而达到时效的目的[1]．由于具有适用性强、节能环保、成本低、周期短等特点，振动时效正逐步得到推广和使用．但由于缺乏对振动时效机理的有效解释，振动时效工艺参数难于确定[2]．从宏观看，目前被多数人认可的解释是动应力与残余应力叠加值达到或超过材料屈服强度时，材料发生屈服，残余应力得以减小．由于工件内残余应力是自平衡应力，其应力状态为复杂应力状态，不同激振方式产生的动应力形态和大小不同，动应力与残余应力叠加后材料的屈服区域不同，残余应力减小和均化的效果也不同．因此，一般工件采用弯曲振动方式的振动时效处理能得到较好的残余应力减小和均化效果，但对于中心轴对称的圆管工件来说，弯曲振动方式的振动时效处理无法提供大而均匀的动应力，因而极大地影响了其振动时效效果，扭转振动可以在圆管截面产生大而均匀的动态剪应力，但扭转振动方式的振动时效(以下简称扭转振动时效)对圆管工件残余应力的减小和均化效果如何，工艺参数如何确定还有待研究．因此，通过模拟圆管对接焊件(以下简称试件)焊接残余应力的产生及扭转振动时效过程，合理确定振动时效工艺参数，分析和探讨扭转振动时效消除残余应力的效果，是非常有意义的．

1 焊接残余应力场的模拟

1.1 焊接模型

焊接模拟试件采用两根长度为100 mm的无缝钢管对接焊接而成，钢管截面尺寸50 mm×5 mm，坡口形式为Y型坡口，钝边高度2 mm，对接间隙2 mm，单面单道焊一次成型．试件材料为25钢，焊接材料选用与母材性能接近的材料．25钢随温度变化的性能参数取值参考文献[3-4]选取．因材料的塑性较好，材料的弹塑性本构关系定义为经典双线性随动强化模型(BKIN)，材料随温度变化的双线性应力应变曲线如图1所示．焊接参数：焊接电流I=130 A，焊接电压U=18 V，焊接速度v=5 mm/s，热效率η=0.75．

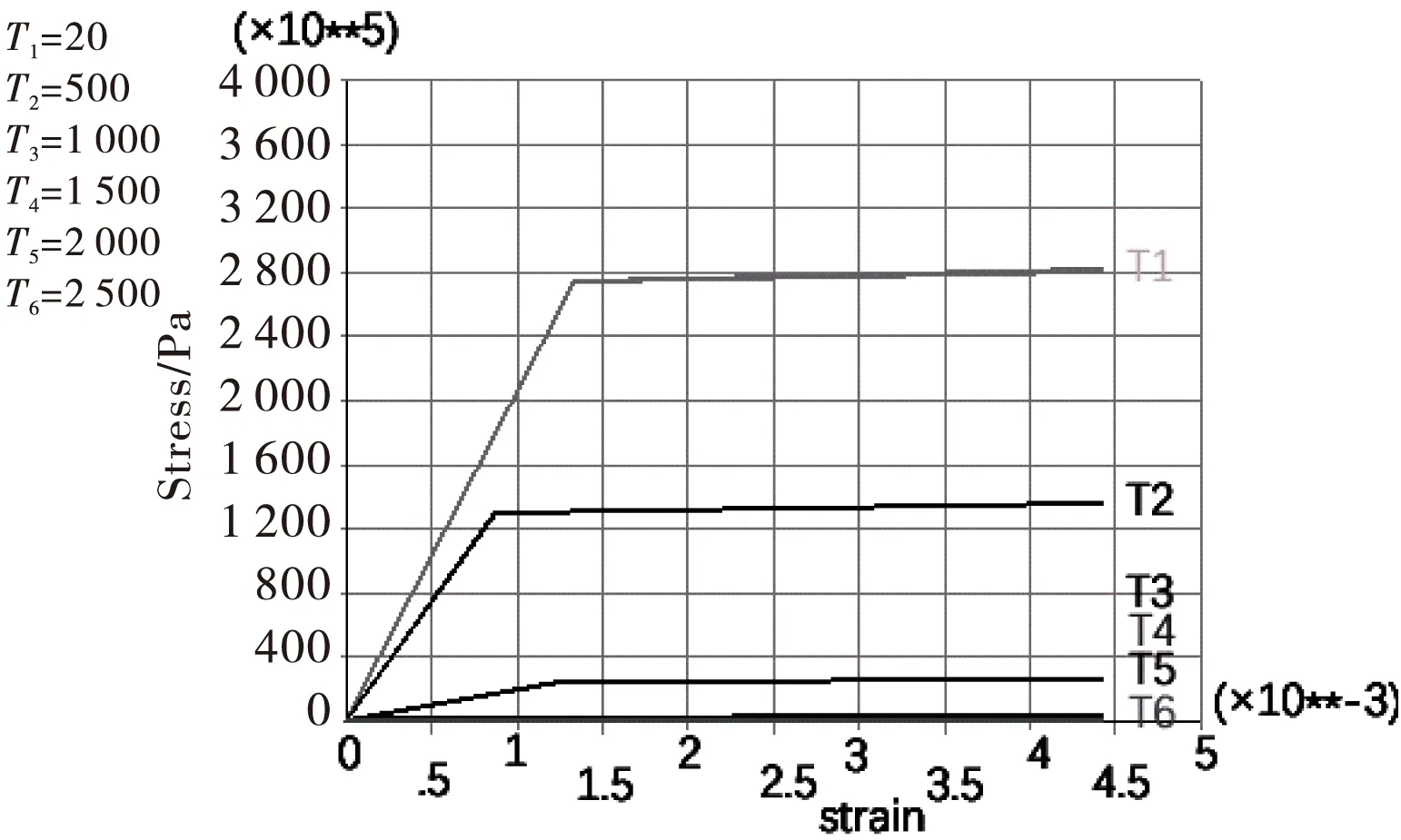
图1 材料在不同温度下的应力应变曲线

温度场计算采用三维热实体单元Solid70划分有限元模型，应力场计算时，转换为对应的三维结构实体单元Solid45．焊缝及其临近区域网格划分较细密，离焊缝远的区域网格划分稀疏，划分网格后的有限元模型如图2所示．根据模型的构造，将所有节点转换至圆柱坐标系下，ρ为径向距离，φ为方位角，z为轴向距离．

1.2 焊接过程模拟与残余应力的获得

热源模型采用基于生死单元技术的热源加载模型，试件的焊接是在焊接热源移动过程中完成的，计算时，利用APDL语言中的do循环语句实现在任一时刻将热源加载在对应位置的单元上．焊接起始点为图2所示模型中φ=0时ρ正向对着的焊缝单元，沿着环向加载一周，分32个载荷步完成．热源加载时间为32 s，冷却时间为2 030 s．

在温度场计算基础上，按时序依次读取节点温度，以体载荷方式加载到对应结构分析模型节点上，时间步长与计算温度场时一致．计算应力应变场时，需设置试件位移边界条件．考虑到焊接时试件的变形自由以及振动时效处理的需要，对试件一端节点施加ρ、φ、z方向自由度约束，另一端约束ρ方向自由度(径向约束)．计算得到的焊接应力场分布如图3所示．

图2 有限元网格模型 图3 等效残余应力分布云图

2 振动时效过程模拟

2.1 振动时效模型

振动时效模型为试件一端固定，另一端径向约束，在径向约束端试件外圆一节点上施加一交变切向力F=Asin(2πft)，进行扭转振动时效处理，振动时效在常温下进行，设在振动时效过程中，材料的应力应变服从双线性随动强化准则(BKIN)，应力应变曲线如图1中T1(=20℃)所对应的曲线．为了考察和分析试件振动时效效果，在试件外表面平行于焊缝方向距焊缝中心两侧5 mm、10 mm及焊缝中心处分别定义路径P1、P2、P3、P4、P5，在垂直于焊缝方向上φ=0(起焊点)的位置定义路径Pa．路径定义如图4所示．

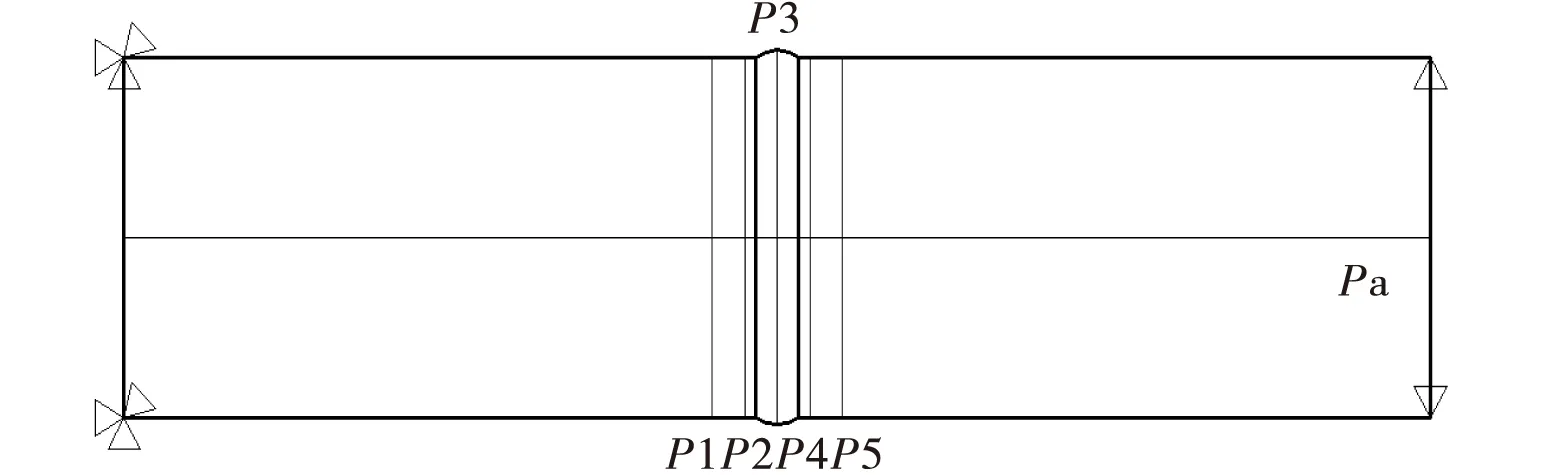
图4 路径定义

2.2 振动时效工艺参数确定

为了确定合理激振频率，首先应对上述约束条件的试件进行模态分析，求解试件的振动特性．经模态分析得到试件前五阶固有频率分别为：3 473.3、3 473.3、3 997.1、6 412.0和6 750.3 Hz，其中3 997.1 Hz为三阶扭转模态振型，在此振型下，试件绕管轴线发生扭转角位移，在此阶固有频率附近容易获得较大的扭转振动，试件横截面上能获得大而均匀的动态剪应力场，因此第三阶振型为理想振型，也是最佳主振振型，其对应的频率3 997.1 Hz为主振频率．结合试件支撑条件，激振点选在试件径向约束端外圆上．

由于随着振动时效的进行，构件的残余应力降低，刚度减小，固有频率左移，主振频率不能作为激振频率，根据文献[5]，应选择亚共振区上升沿主振峰峰值的1/3～2/3所对应的频率作为激振频率．因此要确定激振频率还必须求得试件的幅频特性曲线．对试件进行幅频响应分析后，在试件外表面φ=0的z轴方向焊缝中心及左右对称等距离(间距2 mm)各取2个点考察，这5个点从固定端向外依次定义为A、B、C、D、E点，通过分析这些点的方位角φ随频率的变化关系，得到了试件在主振频率附近的幅频特性曲线(如图5所示)．从图5中可以看出，振幅在主振频率处最大，考察点的响应趋势一致，反映了主振峰的谐波特性．经计算，频率为3 902.1 Hz所对应的幅值为主振峰峰值的2/3，综合考虑，对试件进行扭转振动时效处理的激振频率选择为3 902.1 Hz．

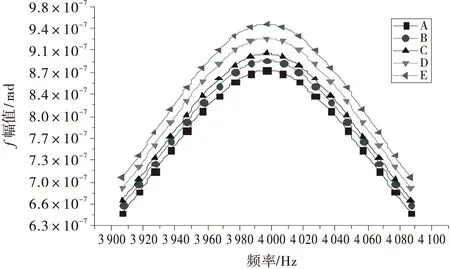
图5 考察点幅频特性曲线

激振力是振动时效的重要工艺参数[6]．从振动时效的宏观机理看，激振力产生的动应力与残余应力的叠加值必须大于等于材料的屈服强度，试件内残余应力才能得以释放．但为了保证试件在激振力作用下不发生疲劳破坏，激振力也不能太大．根据文献[5]，为保证材料不发生疲劳破坏，激振力产生的等效动应力应小于等于材料抗拉强度的1/3，试件材料为25钢，常温下的抗拉强度σb为450 MPa，因此，激振力产生的等效动应力应小于等于150 MPa．由于在扭转振动时效处理时，作用在试件截面上的动应力主要为剪应力，为了较为合理地选择激振力的大小，利用上述模型，分别取激振力幅值A为3 000 N和4 000 N对试件进行瞬态动应力响应分析．由于模拟得到的焊接等效残余应力峰值出现在试件Pa路径上距试件端部90 mm和110 mm的位置，等效应力值达到190.5 MPa，因此，取Pa路径上距试件端部90 mm处的节点为考察点，图6为考察点在激振力幅值A为3 000 N和4 000 N激振力作用下的等效动应力响应曲线．

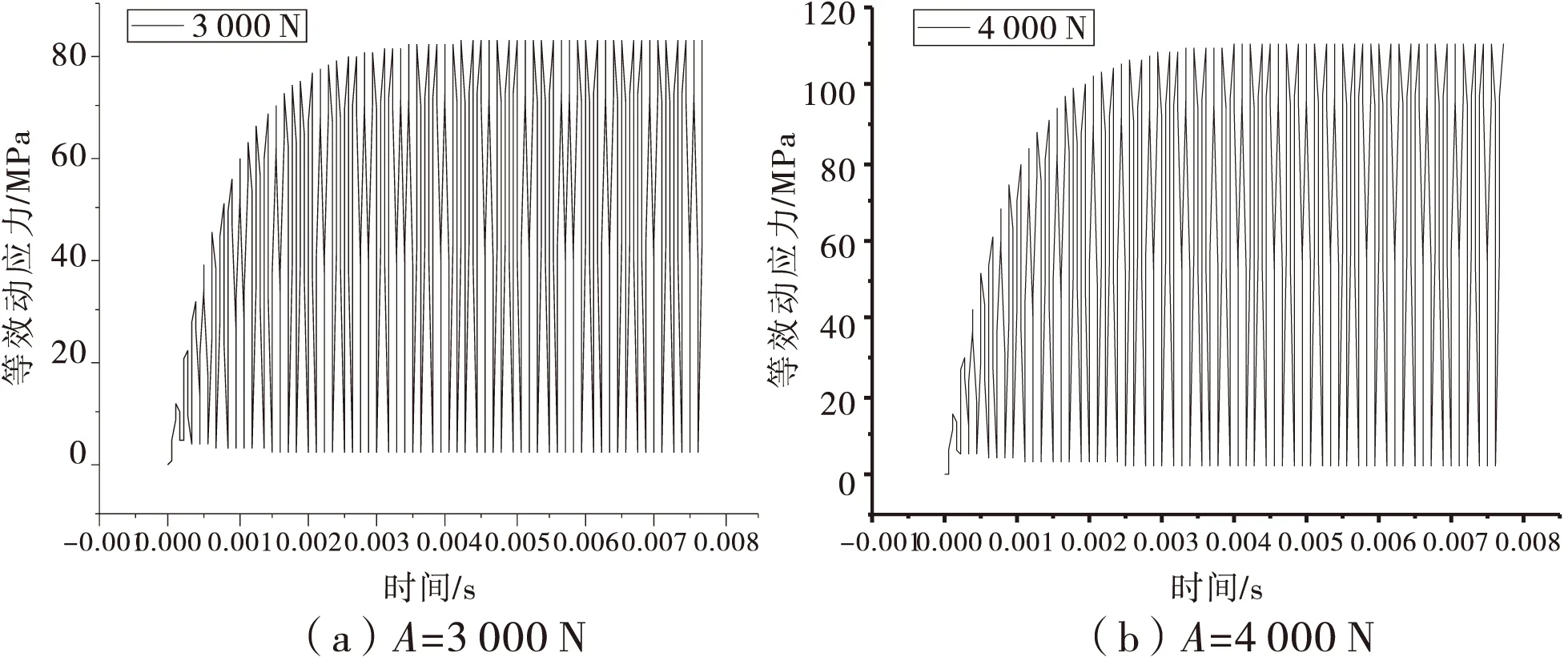
图6 考察点等效动应力响应曲线

从图6可以看出，阻尼的存在，使得结构的响应幅值由零开始逐渐变大，经过11个周期左右达到最大值，也就是经过0.002 8 s左右的时间动应力幅值达到稳定状态，达到稳定状态后，激振力幅值为3 000 N和4 000 N时，考察点处的等效动应力峰值分别为80.0 MPa和110.7 MPa，且激振力幅值越小，考察点处等效动应力峰值越小．因此，试件扭转振动时效处理时，激振力幅值A分别取3 000 N和4 000 N是满足我国机械行业标准要求的．为了探究不同激振力作用下试件扭转振动时效处理效果，试件扭转振动时效处理的激振力幅值A分别取为1 000、1 500、2 000、2 500、3 000、3 500、4 000 N．

振动周期或时间对振动时效影响并不显著，一般情况下残余应力大幅消减发生在前期，增加振动时间反而会降低构件的疲劳寿命[7]．通过各激振力作用下的响应分析可知，在经过11个周期循环加载后，动应力响应幅值和位移幅值都达到稳定，因此，激振时间取为在激振力循环加载20个周期后卸载．

2.3 振动时效过程模拟及结果分析

振动时效过程的数值模拟是通过动力学瞬态分析实现的．针对上述振动时效模型和工艺参数，在焊接应力场模拟基础上，耦合焊接残余应力场，利用重启动分析，保持有限元模型、单元类型、单元属性、边界条件、材料性能等与焊接应力场计算时的设置一致，在同一激振频率(3 902.1 Hz)下，对接试件分别施加7组正弦激振力，分别加载20个周期后卸载，试件停止振动完成振动时效过程的模拟．

图7为试件Pa路径上振前和不同激振力(激振频率为3 902.1 Hz)振后的等效残余应力分布图．从图中可以看出，在激振频率为3 902.1 Hz，分别采用上述7种不同激振力的扭转振动时效处理后，试件Pa路径上振前等效残余应较高的焊缝区及焊缝临近区域，等效残余应力峰值都得到了明显的下降，最大下降量为65.3 MPa，且随着激振力的加大，等效残余应力峰值下降越多；在距焊缝较远的区域，由于振前残余应力较小，振后等效残余应力值变化不大．总体来看，扭转振动时效处理后，试件Pa路径上等效残余应力峰值得到了削减，等效残余应力得到了均化，且随着激振力的加大等效残余应力峰值减小和均化效果越好．

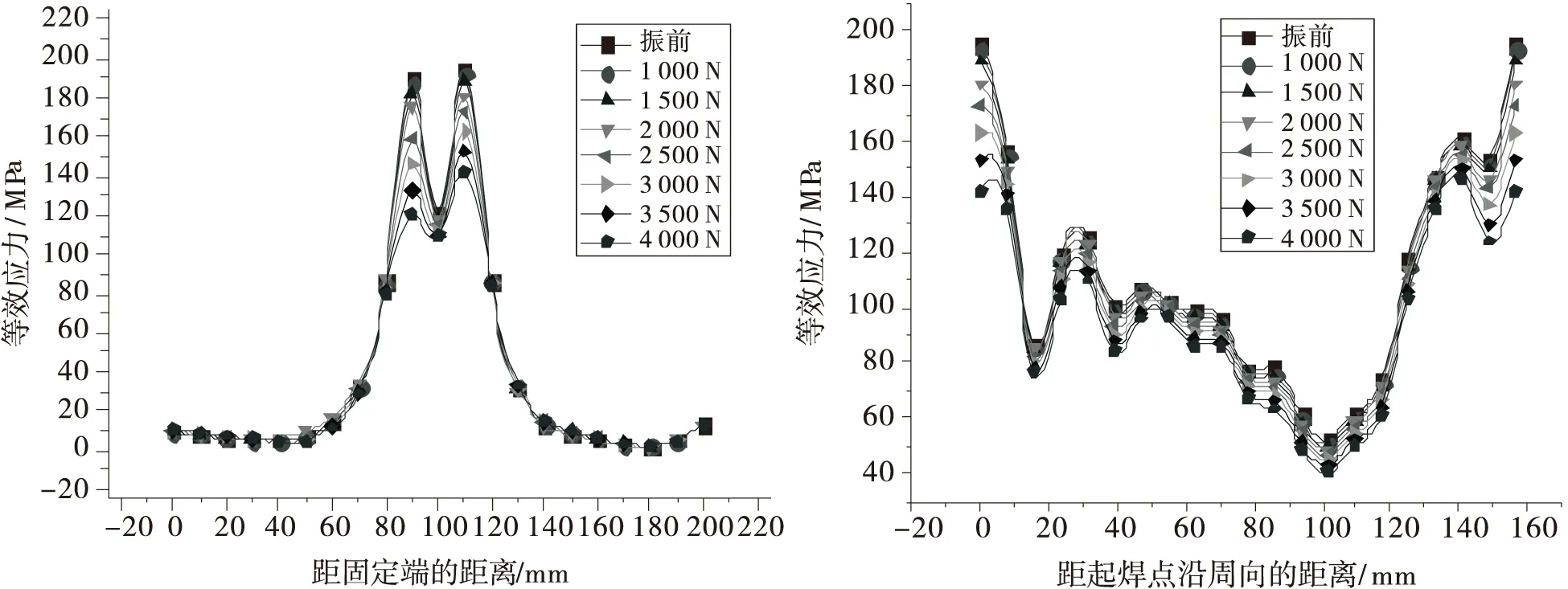
图7 Pa路径上等效残余应力分布图 图8 P2路径上等效残余应力分布图

图8为平行焊缝方向P2路径上振前和不同激振力(激振频率为3 902.1 Hz)振后的等效残余应力分布图．从图8可以看出，在激振频率为3902.1 Hz，采用7种不同激振力分别对试件进行扭转振动时效处理后，试件P2路径上的等效残余应力都有不同程度的减小，且随着激振力的加大，等效残余应力下降幅度增加．其中P2与Pa路径交叉处，等效残余应力降低幅度最大，降幅达到52 MPa，原因是此处振前等效残余应力最大．从图8还可看出，P2路径的中间部分振前等效残余应力值较小，其振前残余应力与动应力叠加后的等效应力并未达到材料屈服强度，但振动时效处理后其等效残余应力也出现了下降．从宏观上看，可能是残余应力是自平衡内应力，振动时效过程中，应力场的再平衡导致部分区域残余应力改变，使得部分原残余应力与动应力叠加值没有达到屈服强度的部位振后也出现了等效残余应力降低的现象．

图9为7种不同激振力(激振频率为3 902.1 Hz)振后，平行于焊缝的5条路径上的等效残余应力均化率图．从图中可看出，P1、P3和P5路径上的等效残余应力均化率较低，且在7种不同激振力作用下变化不大，其原因是P1和P5路径上的残余应力最大值较小，振动时效过程中，动应力与残余应力的叠加值较小，导致这两条路径上的离散度降低幅度较小，残余应力均化率较低，而P3路径上的残余应力分布比其他路径均匀，路径上最大应力下降的同时，路径上的整体应力水平也一起下降，导致这条路径上的残余应力均化率较低．P2和P4路径上的等效残余应力均化率较高，均化效果明显，且随着激振力的增大而增加，在4 000 N的激振力作用下分别达到了37.9%和36.2%．

图9 平行于焊缝路径上的等效残余应力均化率

3 结 论

以圆管对接焊件为例，对焊接残余应力的产生及扭转振动时效全过程进行了数值模拟，合理确定了振动时效工艺参数，分析了不同激振力作用对残余应力消除和均化效果的影响，得出以下结论：1)通过模态分析和谐响应分析，结合振动时效机理和我国有关振动时效的行业标准可以确定出工件振动时效的合理工艺参数．2)采用合理工艺参数，扭转振动时效能够有效减小和均化圆管对接焊件的残余应力，且在激振力和激振频率不变条件下，残余应力越大，残余应力消除效果越好，在激振频率不变条件下，残余应力减小和均化效果，随激振力的增大而增大．

[1] 沈华龙，吴运新，郭俊康．高强度铝合金厚板振动时效工艺的研究[J]．振动与冲击，2009，28(8)：191-194．

[2] 高洪波，付 强，刘 杰．振动时效过程模拟与分析[J]．机械设计与制造，2013(8)：88-91．

[3] 鹿安理，史清宇，赵海燕，等．厚板焊接过程温度场、应力场的三维有限元数值模拟[J]．中国机械工程，2001，12(2)：183-186．

[4] 赵 锐．焊接残余应力的数值模拟及控制消除研究[D]．大连：大连理工大学，2006：29-30．

[5] JB/T10375-2002．焊接构件振动时效工艺参数选择及技术要求[S]．北京：机械工业出版社，2002．

[6] 付建科，范万里，陈维壁．基于有限元法的重大焊接结构振动时效工艺参数研究[J]．机械设计与制造，2008(2)：119-121．

[7] 胡永会，吴运新，陈 磊．基于振动时效仿真的流变塑性模型[J]．中国材料进展，2011，5(30)：40-45．

[责任编辑 张 莉]

Numerical Simulation and Analysis of Vibratory Stress Relief Based on Finite Element Method

Fu Jianke1Xu Liang2Lei Xiaoping3Jin Jun4

(1. College of Mechanical & Power Engineering, China Three Gorges Univ.，Yichang 443002, China； 2. State Grid Henan Electric Power Research Institute, Zhengzhou 450052, China； 3. Power China Guiyang Engineering Corporation Limited, Guiyang 550081, China； 4. Three Gorges Navigation Authority, Yichang 443002, China)

Numerical simulation of the welding process and subsequent vibratory stress relief treating of butt welding for round steel pipe is carried out by finite element analysis; and then the residual stress distribution in welding joint is obtained. Based on the reasonable vibration aging process parameters, the vibration aging process of torsional vibration of the weldment is simulated; and the torsional vibration modes of vibration aging to eliminate the effect of residual stress is discussed also. The results show that the torsional vibration aging treatment can effectively reduce and homogenize the residual stress in the welding process. In addition, the decrease of welding residual stress and the effect of homogenization increased with the increase of excitation force.

residual stresses; torsional vibration; vibratory stress relief; finite element method; numerical simulation

2016-09-26

国家自然科学基金项目(51305232)；湖北省重点实验室开放基金项目(2010KJX02)

付建科(1958-)，男，教授，硕士生导师，主要研究方向为金属结构设计、结构动态分析、大型金属结构制造技术．E-mail：jkfu@ctgu.edu.cn

10.13393/j.cnki.issn.1672-948X.2017.04.016

TH16

A

1672-948X(2017)04-0076-04