Periodic Travelling Wave Solution in a Diffusive Predator-prey System
2017-09-06SONGYongliXUZhou
SONG Yongli ,XU Zhou
(1.School of Science, Hangzhou Normal University, Hangzhou 310036, China; 2. Department of Mathematics, Tongji University, Shanghai 200092, China)
Periodic Travelling Wave Solution in a Diffusive Predator-prey System
SONG Yongli1,XU Zhou2
(1.School of Science, Hangzhou Normal University, Hangzhou 310036, China; 2. Department of Mathematics, Tongji University, Shanghai 200092, China)
In this paper, the existence of the periodic travelling wave solution for a general diffusive predator-prey system is investigated. The condition for the occurrence of Hopf bifurcation in wave equations is provided firstly. Then, taking the diffusion coefficient as the bifurcation parameter, the critical value for the occurrence of periodic travelling wave solution is derived. Finally, the obtained theoretical results are applied to deal with a diffusive predator-prey system with herd behavior and the conditions for the occurrence of the periodic travelling wave solution are obtained. The numerical simulations are also employed to illustrate the theoretical results.
predator-prey system; periodic travelling wave solution; Hopf bifurcation
1 Introduction
Predator-prey model is one of important mathematical models in the eology of populations, which is used to describe the interactions in which one species consumes all or part of another. Periodic activity generated by the predator-prey model is often observed in the nature and the distribution of populations in space is not uniform. This phenomenon is closely related to a periodic travelling wave solution in mathematics, which is a periodic function of one-dimensional space that moves with constant speed in time.
Periodic travelling wave solution of reaction-diffusion equations were extensively studied for the so-calledλ-ωsystem (see, e.g. the review article [1]). For the predator-prey model, there are plenty of works on the travelling wave solution (see [2-4] and references therein), but there are only a few works on periodic travelling wave solution. Recenly, the existence of periodic travelling wave solution for the following predator-prey model with modified Leslie-Gower and Holling type II schemes
(1)
has been studied by Yafia and Aziz-Alaoui[5].
In this paper, we study the existence of periodic travelling wave solution for a general diffusive predator-prey model as follows
(2)
whereu(x,t) andv(x,t) are the prey and predator populations at positionxand at timet,d1>0 andd2>0 are the diffusive coefficients of the prey and predator populations,FandGcan be chosen as different forms depending on the interaction of the prey and predator, and the species.
Setting
and dropping the tilde for simplification of notation, we have
(3)
The rest of this paper is organized as follows: In Section 2, the sufficient condition of the existence of periodic travelling wave solution for system (3) is derived. In Section 3, we apply the theoretical result obtained in Section 2 to study a predator-prey model with herd behavior in the prey species and give some numerical simulationsto illustrate the theoretical results. Finally, the paper ends by a conclusion section.
2 Existence of Periodic Travelling Wave Solution

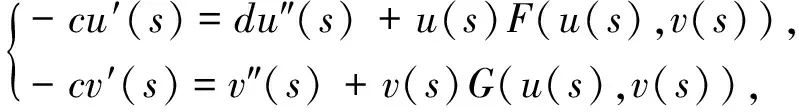
(4)
wheresis called a traveling coordinate and ′denotes the differentiation with respect tos. If system (4) has a periodic solution, then this periodic solution is called the periodic traveling wave solution of system (3) . In the following, we seek the existence of periodic solution of system (4) by Hopf bifurcation theory.
Settingφ(s)=u′(s),ψ(s)=v′(s), system (4) can be written as a system of first order ordinary differential equation in R4
(5)
System (5) has a positive equilibriumE*(u*,v*,0,0). LettingU=(u,v,φ,ψ)T, then the linearized system of system (5) at the positive equilibriumE*(u*,v*,0,0) is

(6)
where
The characteristic equation of (6) is
(7)
where
(8)
For the distribution of roots of Eq.(7), we have the following results.
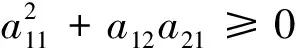
(9)
with -
(10)
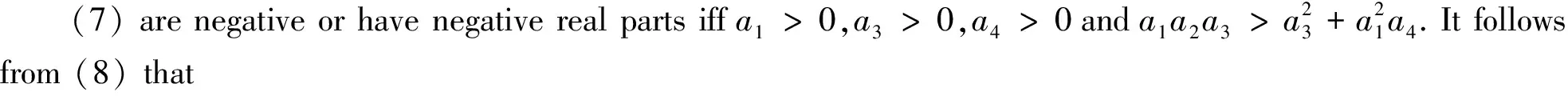
(11)
(12)
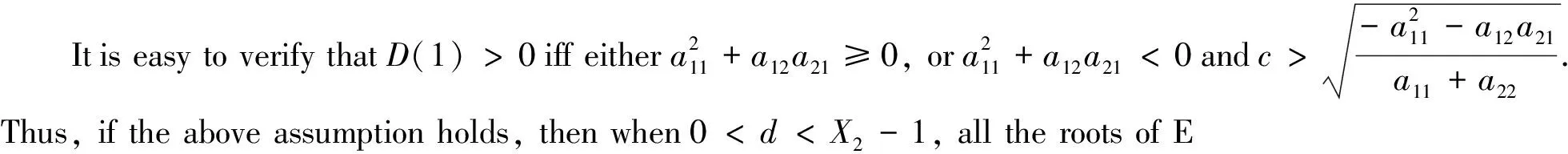
□
Lemma 2 Assume that the conditions in Lemma 1 are satisfied andd0is defined by (9). Then we have the following:
(i) whend=d0, Eq.(7) has a pair of purely imaginary roots ±iω0, where
(13)
(ii) ifλ(d) is a root of Eq.(7) satisfyingλ(d0)=iω0, then (Reλ(d))′d=d0>0.
Proof Assume thatλ=iω(ω>0) is a root of Eq.(7). Then we haveQ(iω,d)=0, i.e.,
Separating the real and imaginary parts, we obtain
(14)
and
(15)
From (15), we have
(16)
Substituting (16) into Eq.(14), we obtain thatD(1+d)=0. This imples that whend=d0andω=ω0, (14) and (15) hold. Therefore, whend=d0, Eq.(7) has a pair of purely imaginary roots ±iω0.
Now we verify the transversality condition. Assume thatλ(d) is a root of Eq.(7) satisfyingλ(d0)=iω0. From Eq.(7), we have
Therefore
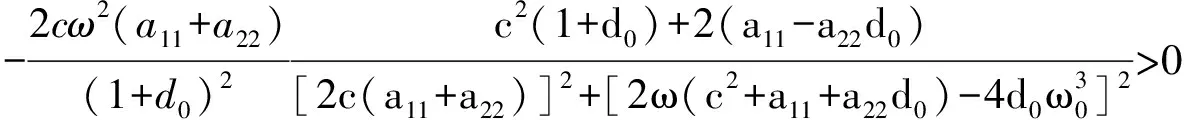
□
ByLemmas1and2,wehavethefollowingresultsonthestabilityandHopfbifurcationforsystem(5).
Theorem1AssumethattheconditionsinLemma1aresatisfiedandd0isdefinedby(9).Thenwehavethefollowing:
(i)thepositiveequilibriumE*ofsystem(5)isasymptoticallystablefor0
(ii)system(5)undergoesaHopfbifurcationatd=d0.
Thefollowingresultfollowsimmediatelyfromtherelationofsolutionsbetweensystem(3)andsystem(5) .
Theorem2AssumethattheconditionsinLemma1aresatisfiedandd0isdefinedby(9) .TheniftheHopfbifurcationofsystem(5)atd=d0issupercritical,thensystem(3)hasstableperiodictravellingwavesolutionsford>d0andsufficientlyclosetod0.
3 Application to a Predator-prey Model with Herd Behavior
Inthissection,weconsiderthefollowingpredator-preymodelwithherdbehaviorinthepreyspeciesundertheunboundeddomainx∈(-,+)
(17)
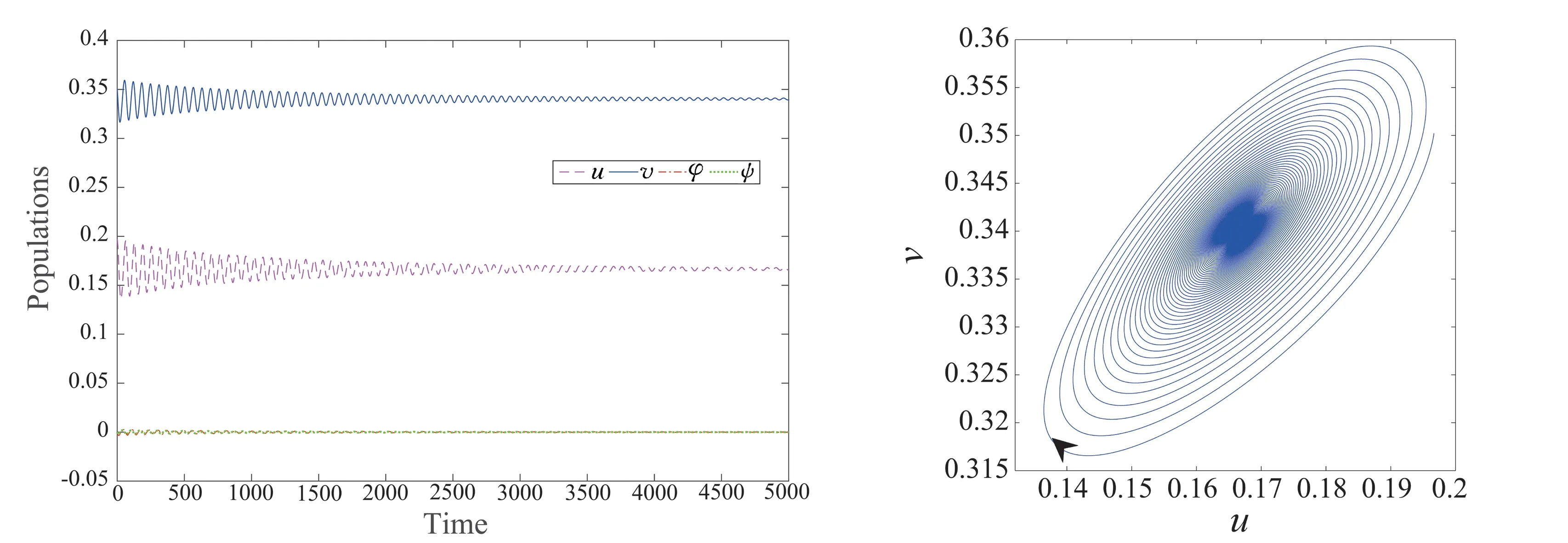
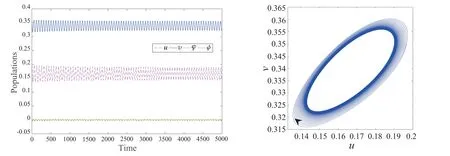
Based on the assumption that the prey exhibits herd behavior and the predator interacts with the prey along the outer corridor of the herd of prey, Braza first proposed the predator-prey model with square root functional responses[6]. Considering the spatial diffusion of populations, the model proposed by Braza[6]was extended a system with diffusion in [7], i.e., system (17). The pattern formation of system (17) has been studied in [7]. Under the bounded domain and considering Neumann boundary condition, the stability and Hopf bifurcation of system (17) has been investigated in [8]. In the following, we investigated the existence of periodic travelling wave solution induced by the diffusion for system (17) under the unbounded domainx∈(-,+)
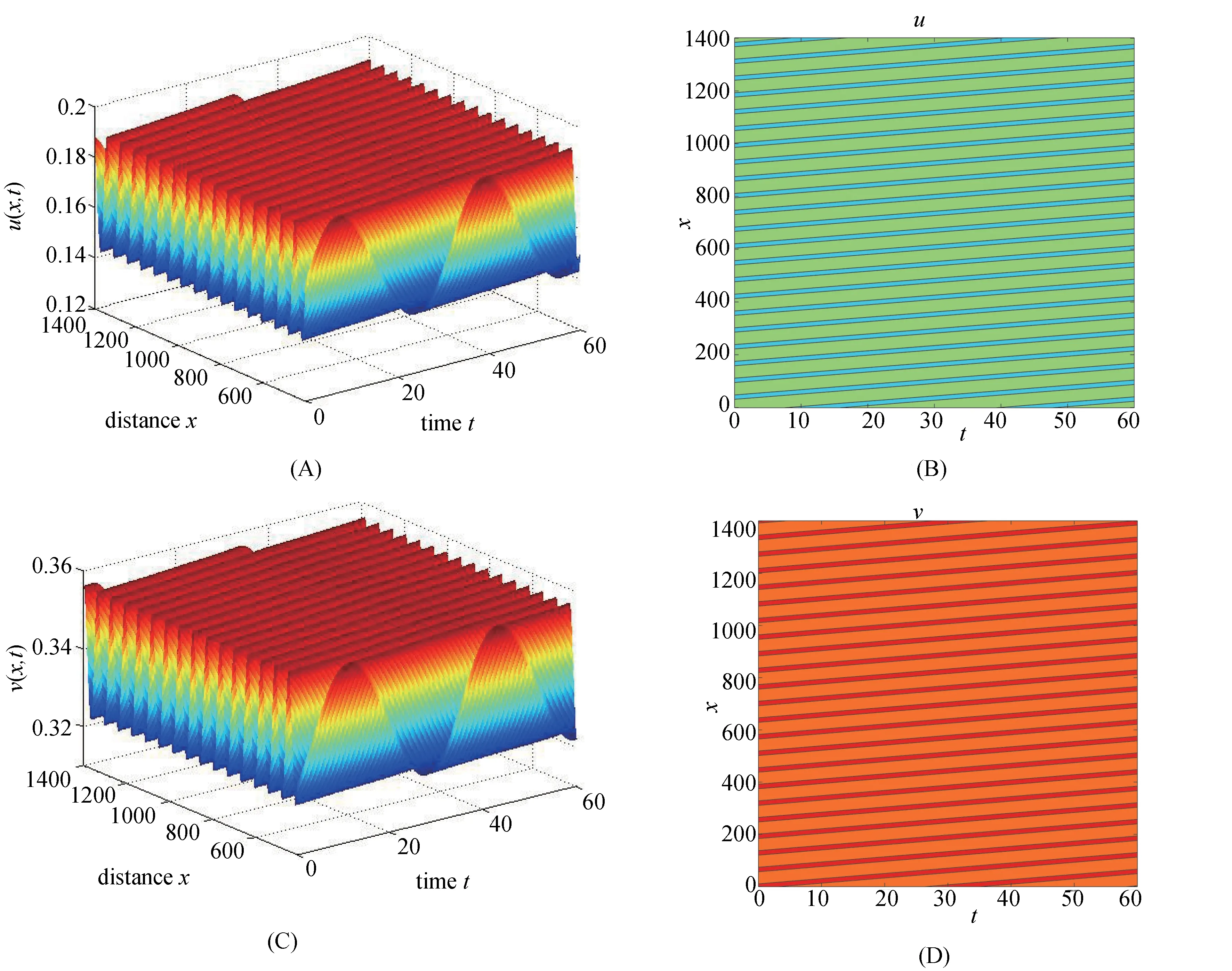
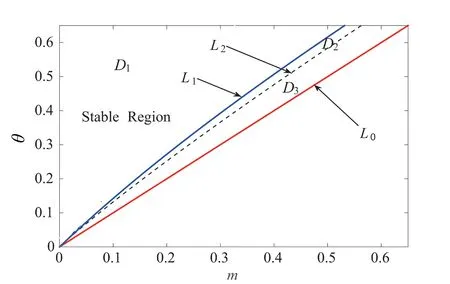
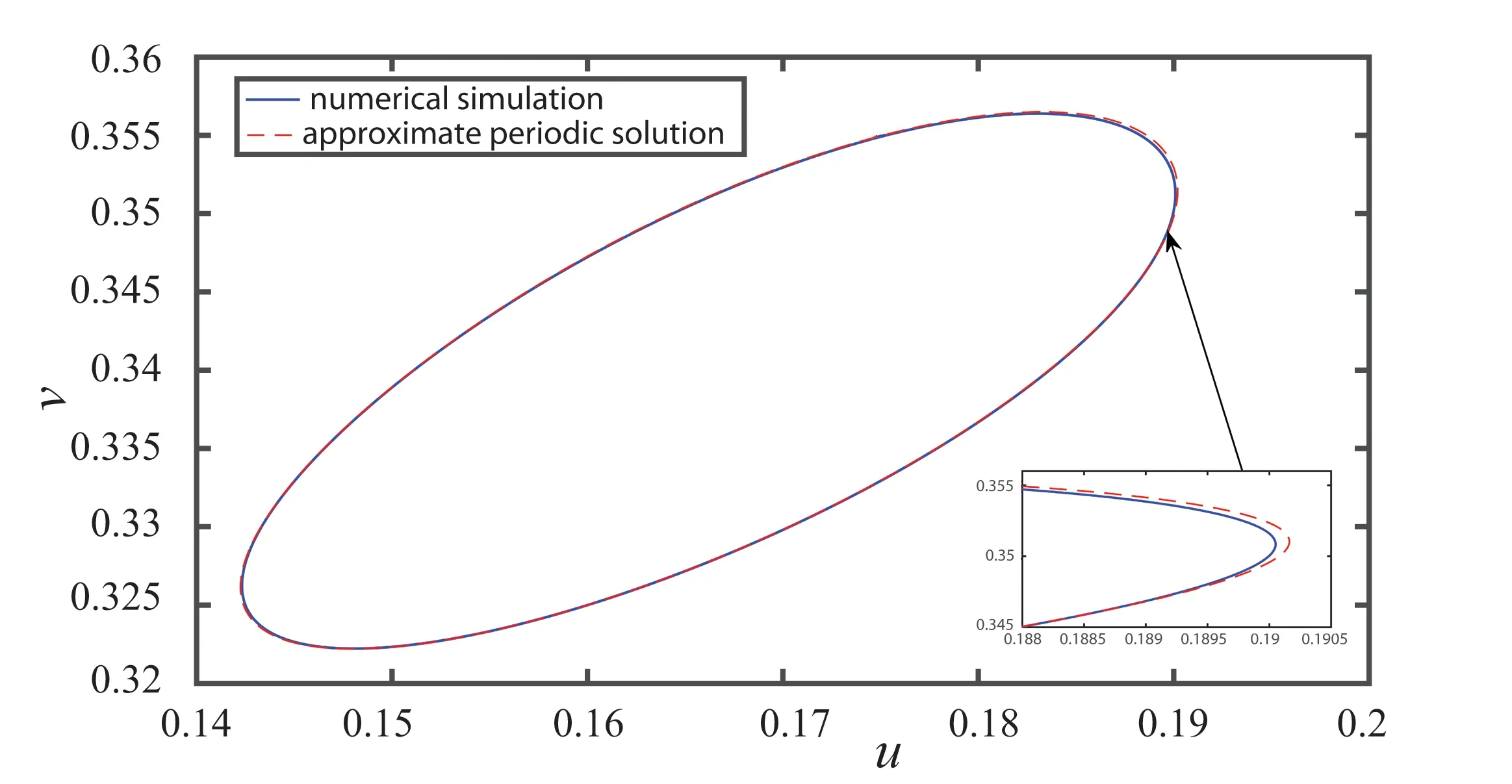
For biological meaning, in what follows we assume 0 From the condition (C), we have (18) It follows from (18) that anda11+a22>0 iff Therefore, in terms of Lemma 1 and Theorem 2 , the following theorem follows immediately. Define the following two curves in them-θplane by and the curveL2is determined by the following implicit function In fact, the curveL2is also a Hopf bifurcation curve for the corresponding ordinary differential system of system (17) . The positive constant equilibrium (u*,v*) of the corresponding ordinary differential system of system (17) is stable in regionD1above the curveL1and unstable in the region between the curvesL0andL1. Fig.1 Bifurcation diagram of system (17) In the following, we numerically illustrate the above results. Taking (m,θ)=(0.5,0.6)∈D2and then choosingc=2, it follows from (9) that d0=3.6717, ω=0.0991. The corresponding wave system of system (17) is (19) Left: the evolution of solution of system (19) for d=3.5 To determine the properities of the Hopf bifurcation, we have to calculate the corresponding normal form associated this Hopf bifurcation. In the following, we use the method developed in [9] to calculate the normal form associated the Hopf bifurcation of system (19) atd=d0=3.6717, and we use the same notations as in [9] . Whend=d0=3.6717, the characteristic values areλ1=iωwithω=0.0991,λ2=-iω, and The eigenvector associated with the characteristic valuesλ1,λ3,λ4are, respectively, DefineP=(Re(v1),-Im(v1),Re(v3),Re(v4)), and denote the right side of system (19) by Then performing the change of variables (20) At this moment, we can follow the procedure in Chapter 2 of [9] to obtain g11=0.3120+0.0570i,g02=0.4811+0.0078i,g20=0.2284+0.4229i,g21=-0.3158-0.1501i, w11=(-0.6876,-0.0010)T,w20=(-0.8295-0.0958i)T and μ2=257.9456, β2=-1.7787, τ2=6.9041. Thus, by the Hopf bifurcation theory in [9], we have the following results on system (19) with (m,θ)=(0.5,0.6)∈D2,c=2 andd0=3.6717 : (i) the Hopf bifurcation is supercritical and bifurcating periodic solutions exist ford>d0; (ii) the Hopf bifurcating periodic solution is orbitally stable; the period of bifurcating periodic solutions increases with the increasing ofd. Fig.3 illustrates these results ford=3.8>d0. Left: the evolution of solution of system (19) for d=3.8>d0; Right: the phase diagram in theu-v plane.Fig. 3 The equilibrium of system (19) is unstable for d>d0 and the Hopf bifurcating periodic solution is orbitally stable Ford=3.8, we can obtain It follows from [9] that the family of approximate periodic solution of system (19) withd=3.8 bifurcating from Hopf bifurcation can be represented by (21) where and This approximate periodic solution (21) can be used for the simulation of periodic travelling wave solution of system (17). Fig.4 shows the approximate periodic solution from (21) and the stable periodic solution simulated in Fig.3. These two periodic orbits are sufficiently close. Fig.4 Comparison of the approximate periodic solution of system (19) represented by (21) with the stable periodic solution simulated in Fig.3 for d=0.38 It follows from Theorems 2 and 3 that if the wave system (19) has Hopf bifurcating periodic solution, then the original system (17) has periodic travelling wave solution. By the above discussion, for (m,θ)=(0.5,0.6)∈D2,c=2 andd=3.8>d0, the wave system (19) has a stable Hopf bifurcating periodic solution as shown in Fig.3. Thus, for (m,θ)=(0.5,0.6)∈D2andd=3.8>d0, the original system (17) has a periodic travelling wave solution with the wave speedc=2. Taking the initial valuesu(x,0) andv(x,0) as defined by (21) and using the periodic boundary condition, Fig.5 illustrates the existence of the periodic travelling wave solution with respect to the time and space variables. In this paper, the sufficient condition for occurrence of periodic travelling wave solution is derived for the general diffusive predator-prey system. Applying the Hopf bifurcation method to the corresponding wave system and in terms of the relationship between the periodic solution of the corresponding wave system and the periodic travelling wave solution of the original diffusive system, we obtain the critical value of diffusion-induced periodic travelling wave solution, which depends on other parameters of the system. Then we consider the diffusive predator-prey system with herd behavior. The dynamics of the system is investigated in the parameter plane ofmandθ. Them-θplane can be divided into three regionsD1,D2andD3. There exist diffusion-induced periodic travelling wave solutions in regionsD2andD3. In regionD2, there exists periodic travelling wave solution or any given wave speedc>0. But for regionD3, there exists periodic travelling wave solution only for the wave speed large enough beyond some critical valuec0. The critical valued0of diffusion coefficient for periodic travelling wave bifurcation is determined by the other system parameters. Numerical simulations are employed to illustrate the existence of diffusion-induced periodic travelling wave solution in the diffusive predator-prey system with herd behavior. (A)the solution for u(x,t); (B) the projector of the solution u(x,t) on the x-t plane; (C)the solution for v(x,t); (D) the projector of the solution v(x,t) on the x-t plane. Fig.5 Periodic travelling wave solution of system (17) with (m,θ)=(0.5,0.6)∈D2 and d=3.8 [1] SHERRATT J A, SMITH M J.Periodic travelling waves in cyclic populations: field studies and reactiondiffusion models[J]. Journal of The Royal Society Interface, 2008, 5(22): 483-505. [2] LI W T, WU S L. Traveling waves in a diffusive predatorprey model with Holling type-III functional response[J]. Chaos Solitons & Fractals, 2008, 37(2): 476-486. [3] ZHANG T, JIN Y. Traveling waves for a reaction-diffusion-advection predator-prey model[J]. Nonlinear Analysis Real World Applications, 2017, 36:203-232. [4] DING W, HUANG W Z. Traveling wave solutions for some classes of diffusive predator-prey models[J]. Journal of Dynamics and Differential Equations, 2016, 28(3/4): 1293-1308. [5] YAFIA R, AZIZ-ALAOUI M A. Existence of periodic travelling waves solutions in predator prey model with diffusion[J]. Applied Mathematical Modelling, 2013, 37(6): 3635-3644. [6] BRAZA P A. Predator-prey dynamics with square root functional responses[J]. Nonlinear Analysis Real World Applications, 2012, 13(4):1837-1843. [7] YUAN S L, XU C Q, ZHANG T H. Spatial dynamics in a predator-prey model with herd behavior[J]. Chaos An Interdisciplinary Journal of Nonlinear Science, 2013, 23(3): 033102. [8] XU Z, SONG Y L. Bifurcation analysis of a diffusive predatorprey system with a herd behavior and quadratic mortality[J]. Mathematical Methods in the Applied Sciences, 2015, 38(14): 2994-3006. [9] HASSARD B D, KAZARINOFF N D, WAN Y H. Theory and applications of Hopf bifurcation [M]. New York: Cambridge University Press, 1981. 扩散捕食-食饵系统的周期行波解 宋永利1,徐 周2 (1.杭州师范大学理学院,浙江 杭州 310036; 2.同济大学数学系,上海 200092) 研究一般的扩散捕食-食饵系统中周期行波解的存在性.首先,给出了波方程组中Hopf分支发生的条件;然后,以扩散系数为分支参数,推导出了周期行波解发生的临界值;最后,应用所得的理论结果研究了一个具有群体效应的捕食-食饵系统,获得了周期行波解存在的条件, 并利用数值模拟例证了所得的理论结果. 捕食-食饵系统;周期行波解;Hopf分支 date:2017-06-04 Supported by the National Natural Science Foundation of China (11571257) and the Scientific Research Start-up Foundation of Hangzhou Normal University (201603). SONG Yongli (1971—), male, Professor, majored in differential equations and dynamical system. E-mail: syl.mail@163.com 10.3969/j.issn.1674-232X.2017.04.005 O19; O29 MSC2010: 35K57; 37G15; 92B05 Article character: A 1674-232X(2017)04-0368-10
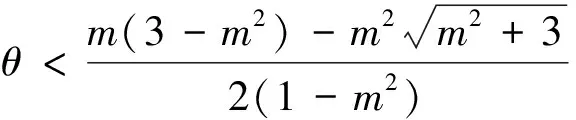
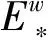

4 Conclusions