深部岩石力学参数随赋存深度变化规律研究
2017-09-03林斌徐冬
林斌 徐冬

摘 要:为了研究煤系地层中赋存深度的变化对深部岩石力学参数的影响,以50m为一个岩层深度范围,通过对淮南矿区潘集背斜上某矿赋存深度在800~1 300m深度范围的同一层泥岩和砂岩样本的单轴抗压强度、弹性模量、泊松比、黏聚力、内摩擦角、抗拉强度等岩石基本物理力学参数的试验研究,采用SPSS19.0对试验结果分别进行统计分析,结果发现,泥岩和砂岩的泊松比均随深度的增加而减小,而这两种岩石其余5个力学参数则随赋存深度而增加,且深度的变化对砂岩力学参数变化影响更大;深度在1 000m附近时,泥岩和砂岩的力学参数都会出现显著变化。
关键词:煤系地层;泥岩与砂岩;试验研究;岩石力学参数;赋存深度;变化规律
中图分类号: TU45 文献标志码:A
文章编号:1672-1098(2017)06-0052-08
Abstract:In order to study on the effect of change in depth on mechanical parameters of deep rock in coal bearing strata, using 50m as a layer depth in this work, Mudstone and sandstone samples were taken from 9 different depths ranging from 800m to 1300m at Zhu Ji mine in Huainan mining area. According to the national standard, some physical and mechanical parameters of rock were obtained, including uniaxial compressive strength, elastic modulus, Poissons ratio, cohesion, friction angle, uniaxial tensile strength, by uniaxial compression tests, variable angle shear tests and Brazilian tests for two kinds of rock respectively after processing. Analyzing all these data respectively with statistics software SPSS19.0, it could be found that the Posissons ration of mudstone and sandstone both got smaller with the increase in depth, while the other five mechanical parameters all got bigger with depth, moreover, the change in depth exerted greater effect on sandstone mechnical parameters, and the mechanical properties of mudstone and sandstone both had significant changes in the depth of around 1 000m.
Key words:coal bearing strata; mudstone and sandstone; experimental study; mechanical parameters of rock; overburden depth;law of changes
随着现代社会的高速发展,各行各业对矿产资源的需求也越来越大,煤矿等矿产资源的开采深度也随之不断增加,伴随而来的工程技术问题和灾害也日益增多,使得深部岩石力学问题受到中外学者的广泛关注。深部岩石与浅部岩石在赋存环境上存在很大差异,即通常所讲的“高应力、高地温、高渗压”,从而造成了深部岩石的力学行为较之浅部岩石更加复杂多变,一些基本力学性能与物理力学参数,如流变特性、强度特性、弹性模量等也随着地层深度的增加而发生很大变化。由此可见,开展深部环境下的岩石力学性质研究很有必要,其中,岩石基本物理力学参数随赋存深度的变化规律,更是意义重大。
在研究深部环境下赋存深度对岩石力学性质的影响方面,许多学者都做出了重要贡献。文献[1-2]通过对不同赋存深度下玄武岩的试验研究,得出了玄武岩基本物理力学参数随赋存深度的变化规律。文献[3]通过试验也得出了花岗岩的弹性模量、抗压强度、抗拉强度随赋存深度加深而增大的观点,并给出了相关数学模型。文献[4]研究发现岩石孔隙率具有随着地层深度增加而减小的规律。文献[5-6]试验研究结果表明岩石在较低围压下表现为脆性,但在高围压下可以转化为延性。深部岩石与浅部岩石所采用的岩石强度理论也不相同,浅部岩石主要采用线性破坏准则,如摩尔-库伦准则,而深部岩石采用非线性准则更加适合,如Hoek-Brown准则[7]。文献[8]也提出一种新的适用于深部岩体的强度准则,该准则考虑了深部岩体的拉伸破坏,同时也考虑深部岩体的剪胀和剪缩破坏。文献[9-10]对不同赋存深度的玄武岩岩样进行了动态断裂韧性测试和单轴拉伸强度测试,得到了动态断裂韧性与拉伸强度之间可能存在一定的关系,并发现动态断裂韧性随着赋存深度的增大而增大的规律。但上述研究主要以火成岩为研究对象,而对于煤系地层的研究涉及不多,本文主要针对这800m以下的煤系地层中典型的砂岩和泥岩地力学特性变化趋势进行试验研究。
1 试验结果与分析
试验样品取自淮南矿区某煤矿详勘钻孔,试验按照《工程岩体试验方法标准》(GB/T50266-99),取样岩层的赋存深度范围为800m~1 200m,以50m为一个岩层深度,将取样岩层划分为9个深度范围,分别以800、850、900、950、1 000、1 050、1 100、1 150、1 200m为界。分别针对不同赋存深度下同一砂岩、泥岩两种岩石,在相同的试验条件测定其单轴抗压强度、抗拉强度和内摩擦角、凝聚力及泊松比,采用SPSS19.0软件对试验结果进行统计分析,以获得上述两种岩石的基本力学参数随赋存深度的变化规律,并对分析结果的显著性差异进行检验。检验采用两种方法,一是:当检验量通过方差齐性检验,即检验量的显著性大于显著性水平0.05,则符合方差检验的前提条件要求,对该检验量进行单因素方差分析,比较方法采用Student-Newman-Keuls(S-N-K)检验法;二是:当检验量不能通过方差齐性检验,即檢验量的显著性不大于显著性水平0.05,则不符合方差检验的前提条件要求,采用多个独立样本检验中的Kruskal-Wallis.H检验法进行分析,检验的步骤为:
1)提出零假設与备择假设H1。
H0:不同赋存深度的岩石,其所检验的基本力学参数的总体分布是相同的;
H1:不同赋存深度的岩石,其所检验的基本力学参数的总体分布是不同的。
2)SPSS将自动计算各组样本(不同赋存深度的岩石参数)的平均秩和H统计量。
如果各组样本的平均秩大致相等,则认为不同赋存深度,其检验量的分布没有显著差异,如果各组样本的平均秩相差很大,则不能认为不同赋存深度,其检验量的分布无显著差异。SPSS会根据H检验临界值表给出H统计量对应的显著性取值,如果显著性取值不大于显著性水平0.05,则拒绝零假设H0,认为不同赋存深度的岩石,其所检验的力学参数的总体分布有显著差异;如果显著性取值大于显著性水平0.05,则接受零假设H0,即认为不同赋存深度的岩石,其所检验的物理力学参数的总体分布无显著差异。
1.1 单轴压缩试验
单轴压缩试验共得到90组泥岩样本试验数据和120组砂岩样本试验数据,根据试验数据可以获得两种岩石各自的单轴抗压强度、弹性模量、泊松比与赋存深度的关系曲线,如图1所示。从图中可以地看出,随着赋存深度越来越大,泥岩与砂岩的单轴抗压强度、弹性模量有逐渐增大趋势,而泊松比具有逐渐减小趋势。
首先对9个不同赋存深度下砂岩和泥岩的单轴抗压强度、弹性模量、泊松比三个量做方差齐性检验,SPSS19.0检验结果如表1所示。
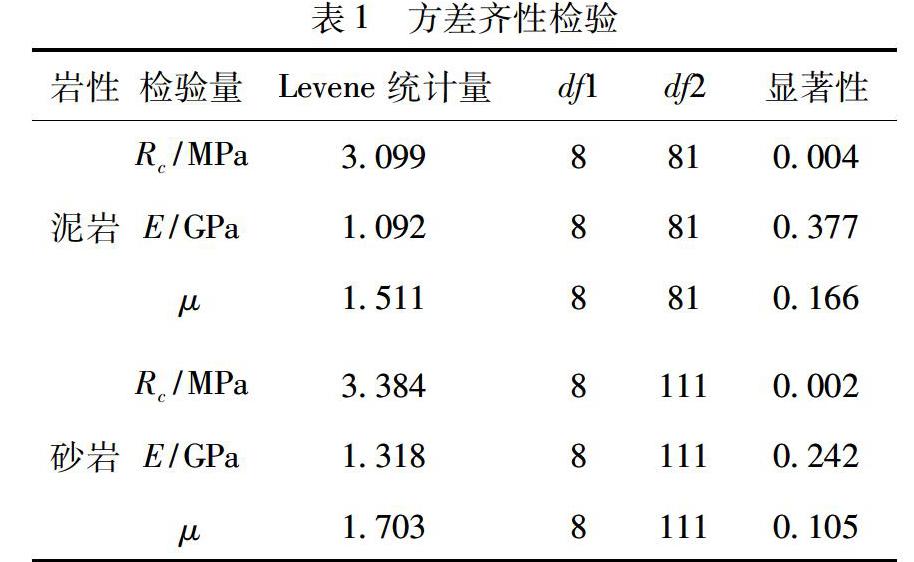
表1中Rc为单轴抗压强度,E为弹性模量,μ为泊松比,Levene统计量是指方差齐性检验(又称Levene检验)中的统计量;df1表示分子自由度;df2表示分母自由度;显著性水平是指:估计总体参数落在某一区间内,可能犯错误的概率,用α表示。如果根据命题的原假设所计算出来的概率小于这个标准,就拒绝原假设;大于这个标准则不能拒绝原假设(下表中相同符号代表同一意思)。
从表1中可发现,在显著性水平α=0.05的条件下,砂岩和泥岩的单轴抗压强度Rc的显著性取值,均小于显著性水平0.05,不符合方差检验的前提条件要求,所以对这两组数据采用Kruskal-Wallis.H方法进行检验,分析结果如表2~表3所示。而弹性模量E和泊松比μ的显著性取值均大于显著性水平0.05,符合方差齐性检验的要求,分析结果如表4~表5所示。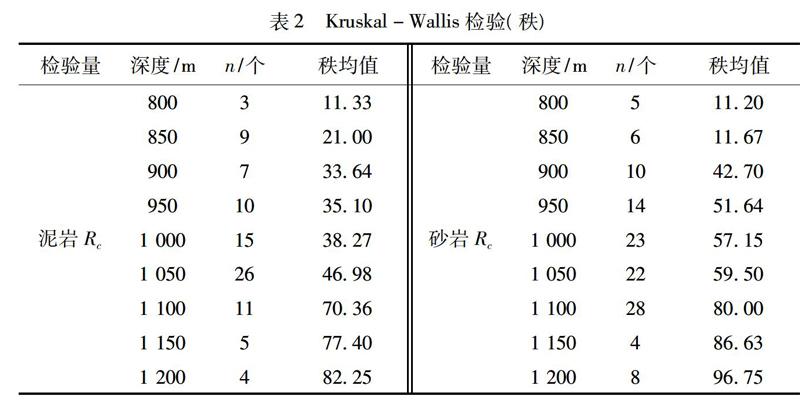
表2表明,两种岩石单轴抗压强度Rc的秩均值都随着赋存深度的增加而增大,其中,泥岩各组样本的秩均值相差较大,在赋存深度超过1 050m时显著增大;砂岩除了800m与850m两个深度的样本秩均值相近外,其余秩均值同样相差较大,在深度超过1 050m时显著增大。表3中两种岩石检验(卡方检验)统计量Rc的渐近显著性取值均为0,所以拒绝零假设,认为不同赋存深度的岩石,其单轴抗压强度的总体分布有显著差异,即赋存深度的增加对砂岩单轴抗压强度的影响较大。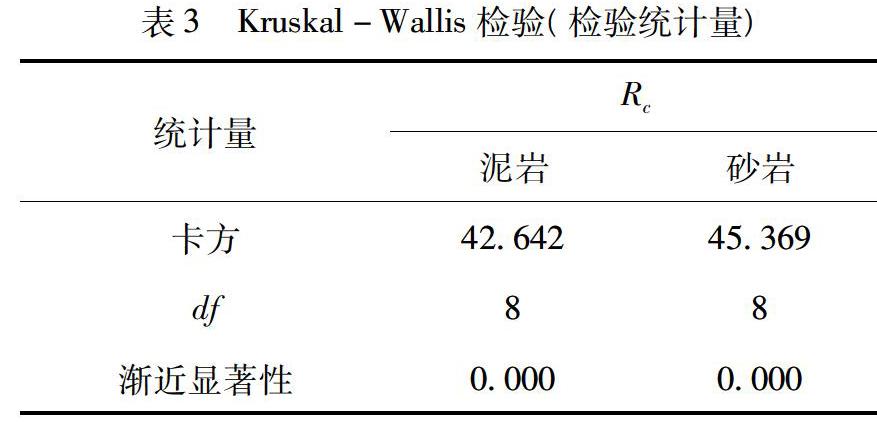
表4显示,泥岩与砂岩样本的弹性模量均值都随着赋存深度的增加而不断增大,其中,泥岩样本在赋存深度超过1 050m时,弹性模量均值发生了显著增大,而砂岩样本在赋存深度超过950m时,弹性模量均值发生显著增大。表5中,赋存深度在800~1 050m的范围内,泥岩样本的泊松比均值基本呈现减小趋势,在1 050m深度处,泊松比均值出现显著减小,超过此深度后泊松比均值随赋存深度增加而减小的趋势变缓,第1亚组的显著性为0.406,远大于0.05,这也反映出深度超过1 050m时泊松比均值减小并不是很显著。砂岩的泊松比均值随着赋存深度的增加也具有类似的减小趋势,但深度在800以上及1 000m以下时,泊松比均值随深度增加显著减小。
1.2 抗剪强度指标试验
抗剪强度指标由变角度剪切试验获得。试验结果得到76组泥岩样本试验数据和78组砂岩样本各自的黏聚力、内摩擦角与赋存深度的关系曲线,如图2所示。试验结果表明,泥岩和砂岩的黏聚力c、内摩擦角均具有着赋存深度的增加而增大的趋势。
两种岩石的黏聚力、内摩擦角的方差齐性检验结果如表6所示。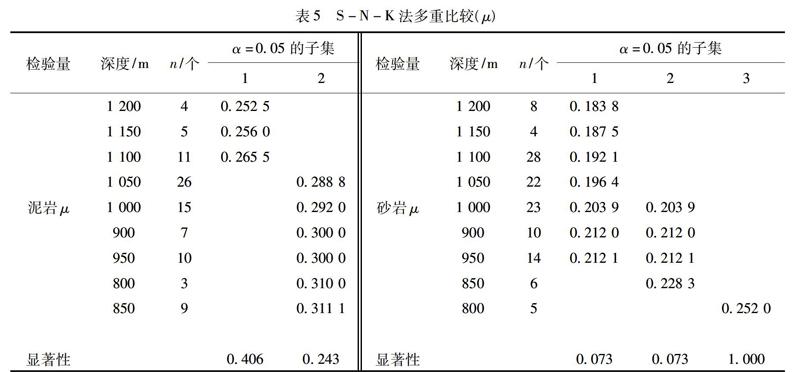


其中泥岩的黏聚力c的显著性取值,小于显著性水平0.05,不符合方差检验的前提条件要求,故对这组数据采用Kruskal-Wallis.H方法进行分析,结果见表7、表8所示。泥岩和砂岩的内摩擦角以及砂岩的黏聚力c的显著性取值,均大于显著性水平0.05,符合方差检验的前提条件要求,分析结果如表9~表10所示。
从表7中可以看出,在赋存深度超过1 050m时,泥岩样本黏聚力c秩均值显著增大。表8中泥岩检验统计量c的渐近显著性取值远小于0.05,所以拒绝零假设,即认为不同赋存深度的泥岩,其黏聚力的总体分布有显著差异。表9中,砂岩样本的黏聚力均值在深度超过1 000m时显著增大。
表10中,随着赋存深度的增加,泥岩与砂岩样本的内摩擦角均值都在不断增大。其中,泥岩样本的增长趋势相对比较均匀,而砂岩样本在赋存深度超过950m时,内摩擦角均值发生显著增大。
1.3 抗拉强度试验
抗拉试验采用巴西法测定岩石样本的抗拉强度。试验结果得到144组泥岩样本和200组砂岩样本的抗拉强度与赋存深度的关系曲线,如图3所示。结果显示,随着赋存深度的增加,泥岩与砂岩的抗拉强度也在逐渐增大。
9个不同赋存深度下两种岩石的抗拉强度Rt的方差齐性检验结果如表11所示。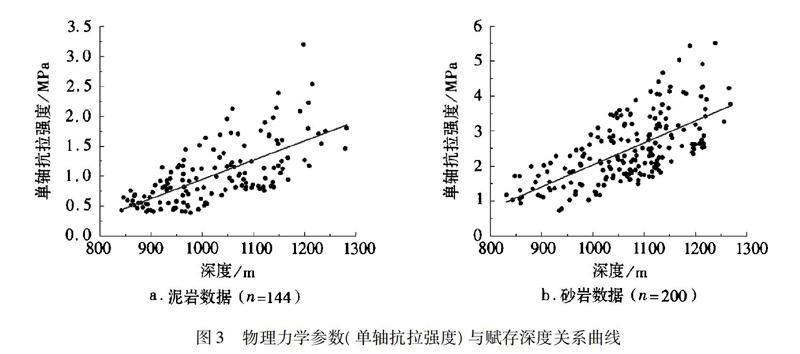
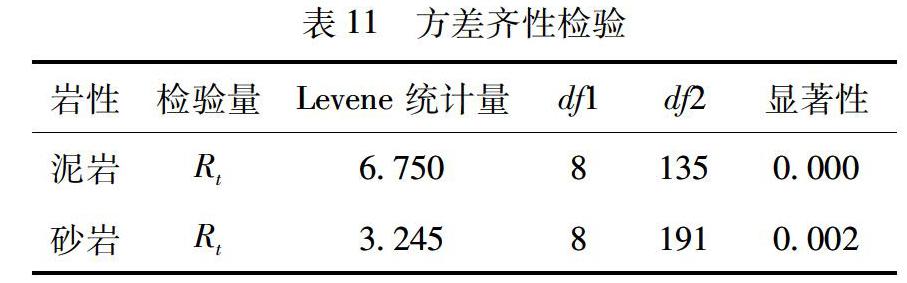
其中砂岩和泥岩的单轴抗拉强度Rt的显著性取值,均小于显著性水平0.05,不符合方差检验的前提条件要求,所以对这两组数据采用Kruskal-Wallis.H方法进行的结果如表12~表13所示。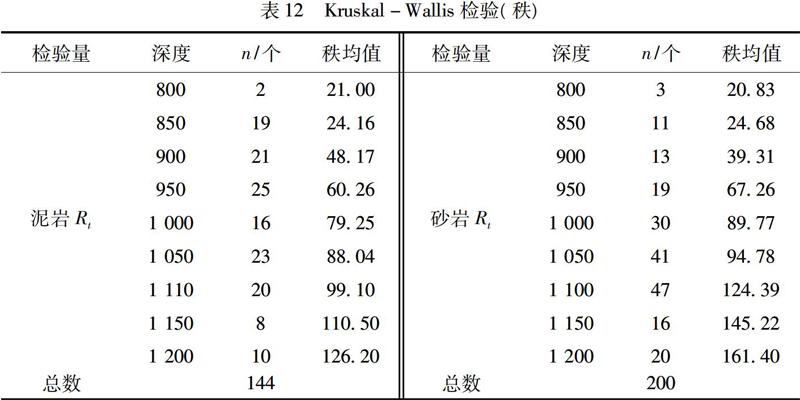

表12顯示,随着赋存深度的增加,两种岩石单轴抗拉强度Rt的秩均值均在增大,且各组样本的秩均值相差都较大。在赋存深度超过950m时,泥岩样本单轴抗拉强度Rt的秩均值显著增大。砂岩样本在赋存深度超过1 050m,单轴抗拉强度Rt的秩均值发生了显著增大。表13中两种岩石检验统计量Rt的渐近显著性取值均远小于0.05,所以拒绝零假设,接受备择假设,即认为不同赋存深度的岩石,其单轴抗拉强度的总体分布有显著差异。
3 结论
通过对煤系地层800~1 200m不同深度范围内泥岩与砂岩的力学参数分析,获得如下的结论:
1)在统计学意义上煤系地层中砂岩和泥岩的单轴抗压强度、弹性模量、黏聚力、内摩擦角、单轴抗拉强度等基本物理力学参数均随着赋存深度的增加而增大;而泊松比则表现出随着赋存深度的增加而减小。
2)深度变化对砂岩力学参数的影响要大于对泥岩力学参数的影响大,其中对内摩擦角表现的最为明显。
3)在赋存深度为1 000m上下时,两种岩石的6个力学参数都会有一个显著变化,其中单轴抗压强度、弹性模量、黏聚力、内摩擦角、单轴抗拉强度这5个参数表现为出现显著增大,而泊松比则出现明显减小。这表明煤系地层在深度达到1 000m附近时,岩石的力学性质出现了较大变化。
参考文献:
[1] 周宏伟,谢和平,左建平. 深部高地应力下岩石力学行为研究进展[J]. 力学进展, 2005, 35: 91-99.
[2] 周宏伟,谢和平,左建平,等. 赋存深度对岩石力学参数影响的实验研究[J]. 科学通报, 2010, 55: 3 276-3 284.
[3] 姜晨光,姜祖彬,刘华,等. 花岗岩岩石力学参数与岩体赋存深度关系的研究[J]. 石材,2004,7: 4-6.
[4] 仵彦卿. 岩石孔隙率随地层深度变化规律研究[J]. 西安理工大学学报, 2000, 16: 69-73.
[5] PATERSON M S.Experimental deformation and faulting in Wombeyan marble[J]. Bull Geol Soc Am, 1958, 69: 465-467.
[6] PATERSON M S, WONG T F.Experimental Rock Deformation: The Brittle Field[J].2nd ed. New York: Springer-Verlag, 2005:2-200.
[7] HOEK E,BROWN E.Empirical strength criterion for rock mass[J].J Geotech Eng ASCE, 1980, 106:1 013-1 035.
[8] 周小平,钱七虎,杨海清. 深部岩体强度准则[J].岩石力学与工程学报, 2008, 27: 119-123.
[9] 满轲. 赋存深度对岩石动态断裂韧性的影响[J].金属矿山, 2011, 417: 19-21.
(责任编辑:李 丽,范 君)
