解读中小学数学教学的衔接点

斯翠梅

长期以来，中小学数学教育各自为阵、相互脱节的现象普遍存在。学生在小学数学中接触的都是较为直观、简单的基础知识，而升入初中后，所学知识在抽象性、严密性上都有一个飞跃，此时，一些学生不能够很快地适应中学的学习方式和学习内容，因为缺乏足够的心理准备而造成学习成绩的下降，甚至会产生厌学怕学、紧张焦虑的不良反应。因此，小学高段教师就需要参考中学的目标和内容，来构建小学高年级数学教学的体系，以发展的眼光看待学生的成长，加强与七年级各方面的衔接，帮助六年级学生顺利迈向新阶段的学习。那么，从小学进入中学数学教学的要求与内容有什么差异呢？中小学数学知识从横向、纵向两方面发展，变化十分明显，这要求教师应当明确知识间的内在聯系，掌握新旧知识的衔接点，才能在教学中做到有的放矢。

从“算术数”到“有理数”

学生刚升入七年级，首先接触到了一个新领域的计算——负数的计算。负数的概念在小学六年级第二学期出现，但只是初步了解，并不涉及负数的计算。因此在正式介入负数概念时，可以结合生活中的实际问题提出。比如，测量温度，当气温在零度以上时，学生能用之前所学的数表示其温度的高低，但当气温在零度以下时，就难以用之前所学的知识表示了。结合这些问题，引入负数表示两个具有相反意义的量，并适当介绍有理数、无理数的概念，使学生感受到数的概念是为解决实际问题的需要而逐渐发展的。

从“数”到“式”的过渡

用字母表示数，实际上是数的概念及其运算法则抽象化、公式化的过程。学生要经历由算术到代数的过渡，主要体现为由数过渡到用字母表示数。字母是代表数的，但它不代表某个具体的数，这种特殊的关系正是七年级学生学习的困难所在。为了克服七年级新生对这一转化而引发的学习障碍，教学中，教师要从小学学过的用字母表示数的知识入手，尽量用一些字母表示数的实例，自然而然地引出代数式的概念。如在人教版五年级上册的第四单元就有《简易方程》一块内容，其中包含用字母表示数、利用天平原理（等式的基本性质）、用方程解决数学问题等教学内容。在教学中，教师既要有意识地穿插利用运算的性质解方程，同时将重点放在用方程解决问题上，由此为学生在后续学习代数搭建了稳定的桥梁，进而降低学生的学习难度。

由“算式”到“方程”的过渡

列方程解应用题是七年级数学的难点。在七年级讲授列方程解应用题时，审题最关键，要设法弄清题意，找出能够表示应用题全部意义的等量关系。

因此，在小学阶段的实际讲授过程中，应当结合教材的安排，有意识地引导学生写出等量关系，并利用等量关系列出方程。另外，尝试利用线段图、列表格的方式等进行分析，这样会降低列方程的难度。在教学中，通过算术方法和列方程的方法对比，让学生进一步明确，有些问题用算术解题不方便，凸显列方程解应用题的优越性，培养学生列方程解应用题的意识。

实验几何到论证几何的过渡

小学教材中，几何知识偏重于计算和具象思维，局限于量一量、画一画、拼一拼、折一折及简单地套用公式计算。小学几何重计算不重逻辑推理，不重视抽象思维。而中学的几何，由已知几何体抽象出几何图形。小学只要求学生对一些几何图形的性质及结论记住就可以了，而中学则要求学生在实验得出结论的基础上，还要从理论上给予证明。对学生的能力提出了新的要求，不仅应具有动手操作的能力，同时还应具备推理论证的能力。

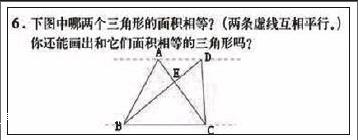
比如，人教版五年级上册教材第87页的练习十六中，有这样一道习题：

师：为了描述方便，我们在三角形的顶点标上字母，然后顺次用字母描述。比如△ABC。图中哪两个三角形的面积相等呢？

生1：△ABC和△BCD。

师：你能说明理由吗？

生1：因为两个三角形的底相同，高也相同。

师：听懂得请举手（超过70%的同学举起了手）。那我们一起来描述一下。△ABC和△BCD的底都是BC，因为AD与BC平行，所以高也相等——平行线间的距离处处相等。所以△ABC和△BCD的面积都相等。这里还有相等面积的三角形吗？

生2：△ABE和△CDE的面积相等。

师：你能说出理由吗？

生2：大的两个三角形面积相等，减掉一个相同的三角形，剩下的也相等。

师：说得真好。因为△ABC和△BCD的面积相等，所以△ABC—△BCE和△BCD—△BCE的面积也相等，即△ABE和△CDE的面积相等。

本例题中有蕴涵着几何的转化思想，教师通过自己的指导，帮学生理清思路，为初中的后续学习打下了基础。

加强中小学衔接已成为新课程下的共识，教师要明确小学高段和初中知识间的内在联系，掌握新旧知识的衔接点，考虑到学生生理与心理发展的渐进性，认真分析研究中小学学生数学学习方法与思维习惯方面的差异，正确引导学生做好从小学数学到初中数学的过渡。endprint