羊毛纤维集合体的分形结构与其保暖性的关系

杨 树， 李玛莎

(嘉兴学院 南湖学院， 浙江 嘉兴 314000)

羊毛纤维集合体的分形结构与其保暖性的关系

杨 树， 李玛莎

(嘉兴学院 南湖学院， 浙江 嘉兴 314000)

针对羊毛纤维集合体结构特征往往难以得到有效表征这一问题，将分形的概念引入羊毛纤维集合体的结构表征，利用计盒维数的方法，计算了5种不同质量的羊毛纤维集合体的分形维数，同时采用平板式保温仪测定了羊毛纤维集合体的保暖性能；随后定量关联了羊毛纤维集合体的分形维数与其基本结构参数和保暖性指标之间的关系。结果表明：利用分形维数来表征纤维集合体的结构特征是可行的，随羊毛纤维质量和体积分数的增大，集合体的分形维数增大，这说明集合体中的纤维结构更杂乱；随分形维数增大，集合体的克罗值和保温率增大，而传热系数减小，即纤维集合体的保暖性增强。

羊毛纤维； 集合体； 计盒法； 分形维数； 保暖性能

分形理论是20世纪后快速发展起来的重要学科之一，用于研究自然界非线性过程所具有的特殊规律性，是描述无序结构特征的有效方法。近几年，分形方法被广泛应用于纺织科学，包括纤维、纱线、织物、纤维集合体等不同领域[1-2]。如在纤维领域，高绪珊等[3]总结了近年来美国和日本对纤维分形结构的研究指出，纤维表面凹凸构造的自相似性与大自然的色光存在对应关系；而在纱线领域，欧健文等[4]将分形理论应用于羊毛纱线的定形，随纤维定形时间的增长，纱线的分形维数增大，纱线结构趋于均匀，并且弹性回复率得到提高，这一结果表明羊毛纤维分形结构的研究对纺织品生产和质量提高具有重要的意义；在织物方面，吴晓晨[5]阐述了分形理论在羊绒织物数码印花等方面的应用。

除纤维、纱线和织物外，纤维集合体如保暖絮片等的结构杂乱无章，但分形学为研究其结构提供了新的、有效的途径。高晶等[6]运用这一特征将纤维复杂的结构简单化，探究了纤维集合体内部的孔隙率、孔洞大小、孔洞分布以及外界条件对分形维数的影响；Fan等[7]通过计算羊毛纤维集合体的分形维数，指出其接近黄金分割点的维数是羊毛具有出色保暖性的原因；本文作者在前期研究中也通过计算非织造布的孔洞面积分形维数，建立起分形维数与其孔洞特征和吸音隔声性能的关系[8]。

针对保暖絮片中常见的羊毛纤维集合体的结构和热学性能的关系，本文引入分形维数的概念，利用计盒维数法计算了5种不同质量的羊毛纤维集合体的分形维数，同时采用平板式保温仪测定了羊毛纤维集合体的保暖性能。随后定量关联了羊毛纤维集合体的分形维数与其基本结构参数和保暖性指标之间的关系。

1 羊毛纤维集合体的分形维数

1973年，美国哈佛大学教授Mandelbrot[9]提出了分形这一概念。分形是对具有统计意义下自相似性[10]的图形、结构或现象的总称，并以数学的形式予以表达。目前关于分形维数的定义主要有豪斯道夫维数、相似维数[11]、信息维数以及容量维数等。本文采用相似维数来定量分析羊毛纤维的内部结构。计算纤维集合体分形维数的具体方法为：首先对羊毛纤维进行图像采集，经过一系列图像处理如图像灰度化、均匀直方图、中值滤波、设定阈值等，得到二值化图像；随后通过MatLab程序[12]计算出羊毛的分形维数。

1.1 纤维集合体图像采集

羊毛纤维为美利奴细羊毛，由嘉兴市吉创纺织品有限公司提供，线密度为11.8 dtex，纤维密度为1.3 g/cm3。将羊毛纤维填塞进边长(a)为 30 cm 的正方形模具中，采用YG141 N型数字式织物厚度仪测量纤维集合体的厚度(h)为7.5 mm。以此标准制作5份体积相同、质量不等的羊毛纤维集合体，每份集合体制作10个相同的样品，以便后续测试计算平均结果。根据下式计算纤维集合体的体积分数：

式中：mf为纤维质量；ρf为纤维密度；a为纤维集合体的边长；h为纤维厚度；V为体积分数。

5种纤维集合体的质量和体积分数计算结果如表1所示。

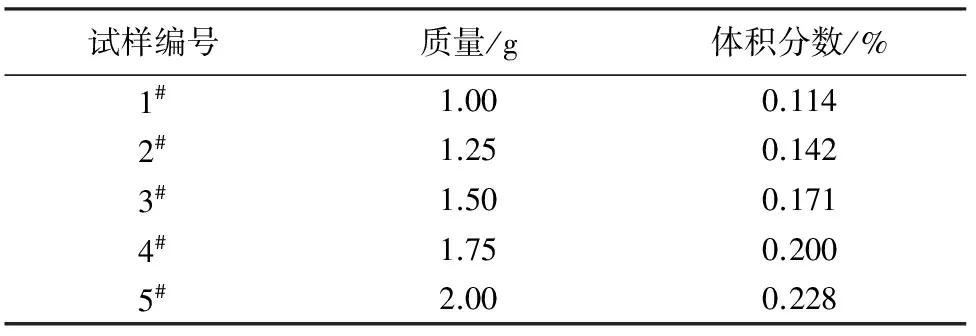
表1 羊毛纤维集合体的质量和体积分数

采用高分辨率的数码相机对羊毛纤维集合体样品的表面图像进行采集，结果如图1所示。由于纤维集合体的厚度较小，因此表面图像也在一定程度上可反映集合体内部的结构特征。

1.2 图像预处理

采用Photoshop软件将图像设置成灰度级，使图像忽略掉其原本的彩色信息，从而达到增强对比度的效果，接着通过直方图均匀化将图像改为均匀直方图分布，直方图表示灰度级在图像像素中的个数，增强灰度范围，使图像对比度更明显，最后进行图像中值滤波[13]确定，消除孤立的噪音点，提高图像的质量。

1.3 图像二值化

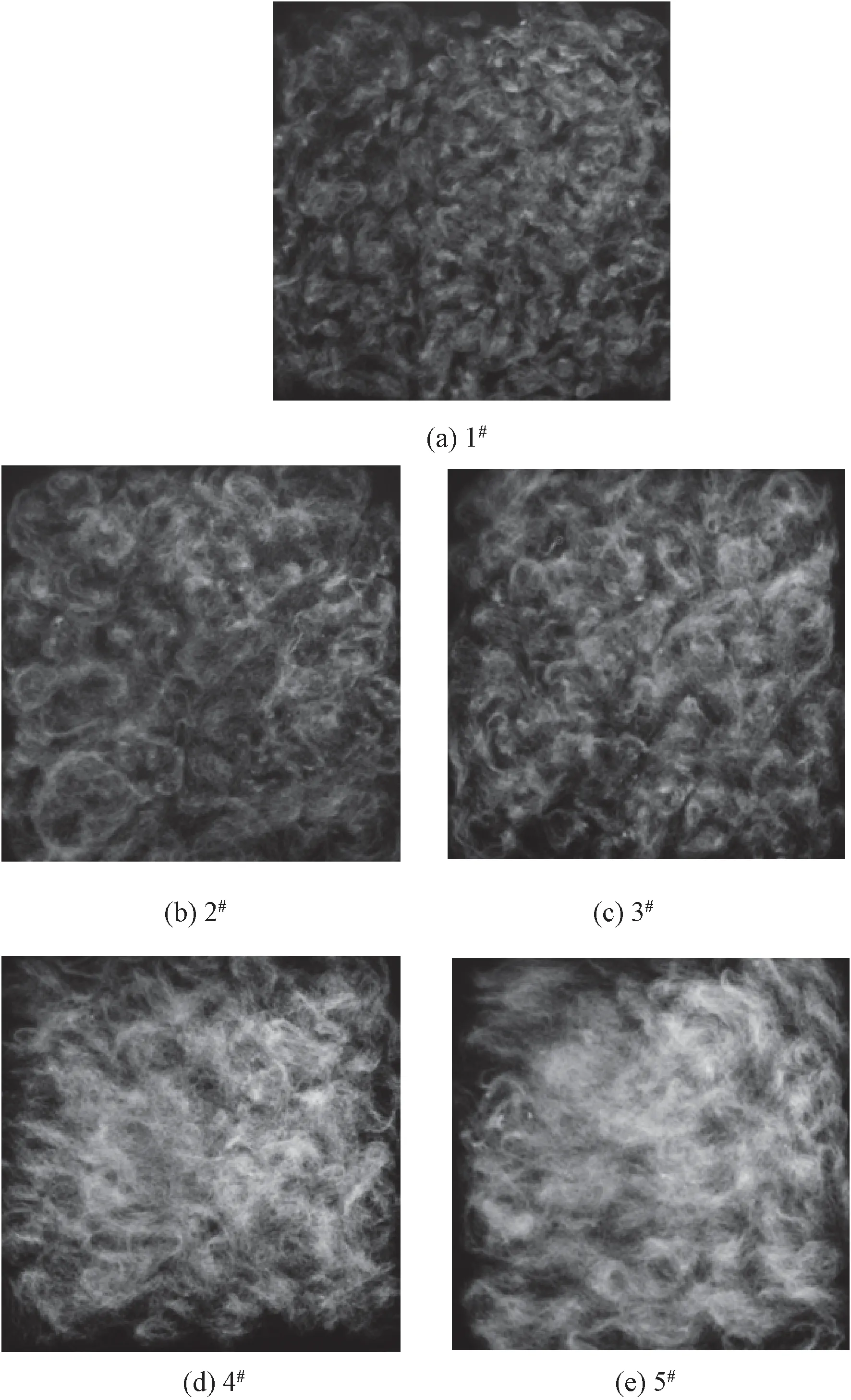
图2 试样照片的二值化图像Fig.2 Image binarization of sample photos

经上述处理再确定一个阈值，并以这个阈值为极限，将多灰度级的图像变成二灰度级的图像，当图像中的某像素点值大于该阈值时，将灰度值设置成255，为黑点；小于或等于这个阈值时，设置成0，即为白点，从而使图像变成清晰的黑白图，即二值化图像[14]，如图2所示。可见经处理后的图像只存在黑白2种颜色，没有杂色干扰，结构特征更为明显，质量越大的纤维几何体，其纤维间的结构更为紧密。

1.4 计算分形维数

盒维数法[15](Sandbox)是Stanley在1985年提出的，不仅适用于自相似的结构，也可用于非自相似性的结构。其计算方法是使用固定边长正方形的盒子盖住扫描得到的图像，计算含有图像纤维的格子数，记为N(∂)，将∂缩小一半，再重复以上步骤，即每个∂对应一个N(∂)值[16]。用∂→0 的方法做r(N)=1/N(1/D) 和lnN(1/∂)的最小二乘法拟合图，其中D代表盒子的大小。该图越接近于一条直线，说明分形特征越明显，直线的斜率即为分形维数。

本文利用MatLab编写程序计算5种羊毛纤维集合体的分形维数，计算过程中拟合的图形接近直线，这说明样本的分形特征较为明显，由此得到5种试样的计盒分形维数值，从试样1#到5#分别为1.624、1.663、1.697、1.725和1.756。

1.5 分形维数与结构参数的关系

接下来开始建立纤维集合体的分形维数与其纤维质量、体积分数之间的关系。将羊毛纤维集合体分形维数结果与纤维质量作比较，结果如图3所示。由图可见，纤维分形维数与质量之间成正相关关系，纤维质量越大，分形维数越大。将羊毛纤维集合体分形维数结果与纤维体积分数作比较，得到如图4所示的结果，R2=0.994 18，即体积分数的与分形维数的相关性是较好的，随着纤维体积分数逐步增大，分形维数也越来越大。

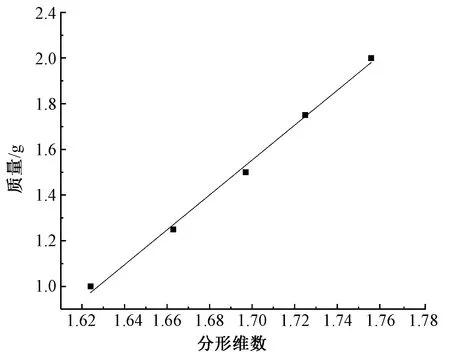
图3 羊毛分形维数与纤维质量的关系Fig.3 Relationship between fractal dimension and mass of wool fiber

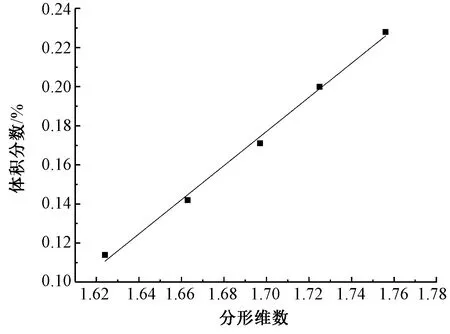
图4 羊毛分形维数与纤维体积分数的关系Fig.4 Relationship between fractal dimension and volume fraction of wool fiber

纤维集合体的分形维数从本质上来说表达的是集合体内部的结构杂乱度，即纤维内部结构越杂乱和无序，其分形维数越大，反之亦然，随集合体内部纤维质量和体积的增加，纤维与纤维之间的排列势必会越来越杂乱，因此其分形维数也会增加。这也证实了分形维数可表征集合体内部结构无序度的可行性。

2 羊毛纤维集合体的保暖性能

羊毛的保暖性能主要由3种指标来表征，分别是克罗值、保温率和传热系数。依据ASTM C1044—2012《使用单面护热板设备或薄型加热器设备的标准实施规程》，采用YG606 型平板式保暖仪进行。测试过程中首先进行空板试验，底板的温度设定为36 ℃，预热时间为30 min。然后将5份试样依次覆盖在测试验板上，试验板为30 cm×30 cm的正方形，因此试样可将试验板完全覆盖，将试验板、保护板和底板都设置为相同的温度，进行测试。测试3次后，得到3个热学指标的平均值，结果如表2所示。

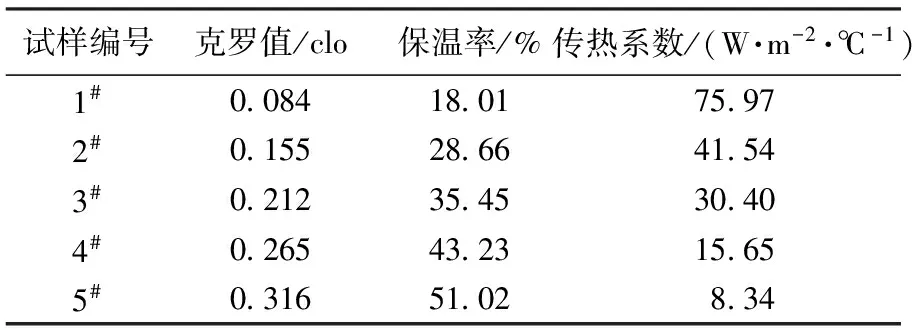
表2 试样的保暖性能参数

3 羊毛分形维数与保暖性能的关系

图5示出克罗值、保温率和传热系数与羊毛纤维分形维数的关系。由图5(a)可知，克罗值的大小与纤维分形维数呈正相关关系，且具有很高的相关度，可见分形维数越大，克罗值越大，即保暖性能越好。如图5(b)所示，羊毛纤维集合体的保温率随分形维数的增大而增加，说明纤维集合体结构的杂乱程度增大，保暖性增强。由图5(c)可看出，传热系数随纤维分形维数的增大而减小，二者呈反相关关系，即随着分形维数变大，纤维间传热速率减缓，则纤维集合体的保暖性能增加。

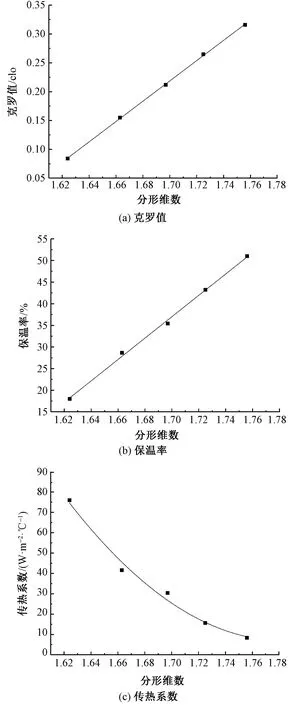
图5 羊毛纤维分形维数与各参数之间的关系Fig.5 Relationship between fractal dimension and clo value(a), insulation rate(b) and heat transfer coefficient(c)

4 结 论

本文将分形的概念引入纤维集合体的结构表征中，利用MatLab编程计算了不同质量和体积分数的羊毛纤维集合体的分形维数，并测试了其热学性能，建立了纤维集合体的分形维数与其结构参数和热学指标之间的关系。

1)利用计盒法分形维数的计算方法得到羊毛纤维集合体的分形维数值发现，分形维数与其纤维质量、体积分数几乎呈线性增大关系，说明非整数的数值可直观反映羊毛纤维结构的杂乱程度，也表明羊毛纤维集合体内部结构具有很强的分形特征。

2)测定了不同质量的羊毛纤维集合体的保暖性能，并建立了其保暖性指标和分形维数之间的关系发现，随着纤维集合体分形维数的增大，其克罗值和保温率也随之增大，而传热系数减小，即整体上保暖性能增强。

[1] 朱志宝, 白永强. 分形几何及其应用[J]. 价值工程, 2012, 31(35): 5-7. ZHU Zhibao, BAI Yongqiang. Fractal geometry with its application[J]. Value Engineering, 2012, 31(35): 5-7.

[2] 王海毅, 田耀斌, 郑新苗. 基于分形理论的微纤维玻璃棉绝热纸的结构与性能研究[J]. 陕西科技大学学报(自然科学版), 2016, 34(5): 1-4. WANG Haiyi, TIAN Yaobin, ZHENG Xinmiao. The study on structure and performance of micro fiber glass paper based on fractal theory[J]. Journal of Science and Technology in Shanxi University (Nature Science Edition)， 2016,34(5):1-4.

[3] 高绪珊, 庄毅. 天然纤维的分形结构和分形结构纤维的开发[J]. 合成纤维工业, 2000, 23(4): 35-38. GAO Xushan, ZHUANG Yi. Fractal structure of natural fiber and exploitation of fiber composed with fractal [J]. Synthetic Fiber Industry, 2000, 23(4): 35-38.

[4] 欧健文, 姚金波, 李淑红, 等. 分形理论在羊毛纱线定形中的应用[J]. 纺织学报, 2011, 32(5):33-37. OU Jianwen, YAO Jinbo, LI Shuhong, et al. Application of fractal theory in wool yarn setting[J]. Journal of Textile Research, 2011, 32(5): 33-37.

[5] 吴晓晨. 基于分形学的羊绒织物数码印花仿扎染图案设计研究[D]. 呼和浩特：内蒙古工业大学, 2014：3-4. WU Xiaochen. The study of digital print of cashmere based on fractal theory[D]. Hohhot:Inner Mongolia University of Technology, 2014:3-4.

[6] 高晶, 于伟东, 潘宁. 羽绒纤维及其集合体结构和性能的研究[D]. 上海:东华大学,2006: 5-7. GAO Jing, YU Weidong, PAN Ning. Study on structure and property of eiderdown[D]. Shanghai: Donghua University, 2006: 5-7.

[7] FAN J, LIU J F, HE J H. Hierarchy of wool fiber and fractal dimension [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2008, 9(3):293-296.

[8] 杨树, 于伟东, 潘宁. 非织造布的孔洞分形维数对其吸声性能的影响[J]. 纺织学报, 2010, 31 (12): 28-32. YANG Shu, YU Weidong, PAN Ning. Effect of nonwovens pore fractal dimension on their acoustic absorption behaviors[J]. Journal of Textile Research, 2010, 31(12): 28-32.

[9] SONG W F, YU W D. Heat transfer through fibrous assemblies by fractal method[J]. Journal of Thermal Analysis and Calorimetry, 2012, 110(2): 897-905.

[10] TANG H P, ZHU J L, XI Z P, et al. Impact factors of fractal analysis of porous structure[J]. Science China Technological Sciences, 2010, 53(2): 348-351.

[11] YIN Y, YANG F, LI Y, et al. Fractal geometry and topology abstracted from hair fibers[J]. Applied Mathematics and Mechanics, 2009, 30: 983-990.

[12] 兆礼, 春晖, 晓丹, 等. 现代图像处理技术及 Matlab 实现[M]. 北京：人民邮电出版社, 2001: 21-23. ZHAO Li, CHUN Hui, XIAO Dan, et al. Modern Image Processing Technology and Matlab Realize[M]. Beijing: Post & Telecom Press,2001: 21-23.

[13] KLEEFELD A, BREUB M, WELK M, et al. Adaptive filters for color images:median filtering and its extensions[C]//[s.n.].International Workshop on Computational Color Imaging.[S.l.]: Springer International Publishing, 2015: 149-158.

[14] CHAKI N, SHAIKH S H, SAEED K. Exploring Image Binarization Techniques[M]. New Delhij: India Springer, 2014: 5-16.

[15] SHOU D, FAN J, DING F. A difference-fractal model for the permeability of fibrous porous media[J]. Physics Letters A, 2010, 374(10): 1201-1204.

[16] MANCUSO S. Fractal geometry-based image analysis of grapevine leaves using the box counting algorithm[J]. VITIS-Journal of Grapevine Research, 2015, 38(3): 97.

Relationship between fractal structure and warmth retention properties of wool fiber assembly

YANG Shu， LI Masha

(NanhuCollege,JiaxingUniversity,Jiaxing,Zhejiang314000,China)

Wool fiber assembly is a porous media whose structure is too complicated to be characterized. To solve this question, the concept of fractal was introduced to fiber assemblies. A box-counting method was used to calculate fractal dimension, and a flat fabric heat retention tester was adopted to test thermal properties of wool fiber assemblies. Then quantitative relation between the fractal dimension and basic structural parameters and thermal properties were acquired. Results indicate the fractal dimension is applicable in characterizing the structure of fiber assemblies, and increases with the increase of the fiber mass and volume fraction, showing more complicated structure. Furthermore, the CLO and warmth retention rate increase with increases of the fractal dimension, while the heat transfer coefficient tends to decrease, i.e. the warmth retention property of fiber assemblies is enhanced.

wool fiber; fiber assembly; box-counting method; fractal dimension; warmth retention property

10.13475/j.fzxb.20160806405

2016-08-27

2017-02-22

国家自然科学基金项目(51403078)；浙江省教育厅科研项目(Y201226223)

杨树(1985—)，女，讲师，博士。主要研究方向为纺织材料。E-mail：yangshu5678@163.com。

TS 102.3

A