数据驱动紧框架在灰色图像去噪中的应用

范立静，王 聪

（河海大学 理学院，江苏 南京 211100）

数据驱动紧框架在灰色图像去噪中的应用

范立静，王 聪

（河海大学 理学院，江苏 南京 211100）

针对去除灰色图像中的泊松噪声从而进一步进行图像分析的目的，采用了基于数据驱动紧框架的含泊松噪声的图像去噪变分模型，并通过了重新赋权的分裂Bregman算法解该模型。结合Matlab仿真实验以及PSNR指标对该算法的图像去噪效果进行评估，评估结果表明该算法可行、有效。

数据驱动紧框架；泊松噪声；图像去噪；分裂Bregman算法

图像去噪是图像处理中的基本问题之一。现如今，已经存在了大量的算法能够解决含高斯噪声的图像去噪问题。但是，含泊松噪声的图像去噪问题依然很少被研究。泊松噪声，一般会在由数量少的光子产生的图像中观察到，例如荧光显微镜检查、发射X线体层照相术等等。

最近十多年来，对于去除灰色图像中泊松噪声的研究取得了一定进展。例如，Csiszár[1]最早提出了Kullback-Leibler（KL）-divergence保真项用于去除灰色图像中的泊松噪声。Luisier等[2]在小波变换中构造了一个SURE估计量用于泊松噪声的去除。Gong等[3]提出了一个l1+l2保真项去除泊松噪声及一切未知噪声。最近，Zhang等学者[4-5]使用重新赋权的l2方法逼近KL-divergence保真项，从而实现了去除泊松噪声的目的。

由图像去噪模型的发展历程来看，变分模型在图像去噪中的应用是最广的。最常用的一种变分模型是 Rudin-Osher-Fatemi（ROF）模型[6]。 ROF 在具有分段时长的图像去噪如二进制图像（文本和条码）时十分有效。在ROF模型被提出之后，许多学者又衍生出了许多其他类型的变分模型[7-12]。其中，基于小波框架的变分模型[14-19]被成功应用于图像去噪中。研究表明，基于小波框架的变分模型比其他变分模型例如ROF模型更好，这是因为小波框架的多分辨率结构和冗余。此外，Cai等[20]最近建立了小波框架和变分模型之间的联系。这种联系给出了基于小波框架的变分模型优于其他某些变分模型的理论依据，即基于小波框架的变分模型可以根据潜在的解的奇点的顺序，在给定图像的不同区域中自适应地选择微分算子。最近，在小波紧框架的思想鼓舞下，Cai等[20]又基于图像数据结构特征，提出了一种数据驱动紧框架，该框架比以往的模型更能精确地重构图像。

文中采用基于数据驱动紧框架的变分模型去除灰色图像中的泊松噪声。其中，赋权的范数项作为保真项，包含数据驱动紧框架的l1范数项作为正则项。然后，又提出了解该模型的重新赋权的分裂Bregman算法。最后，文中又进行了数值实验对所提出的模型和算法进行了验证。

1 背景知识

1.1 变分模型理论

观测图像f的一般表达形式为

其中，u为原始未知图像，ε为噪声扰动。若噪声为泊松噪声，那么泊松噪声服从泊松分布y～P（y），其概率密度函数为

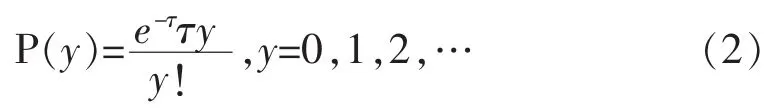
其中，τ是随机数的期望值和方差。

用于图像去噪的变分模型一般表示为

其中，F（u）为保真项，G（u）为正则项。λ＞0 是用于平衡保真项 F（u）和正则项 G（u）。 F（u）由似然函数得到，与噪声特性有关，G（u）是基于u的先验假设得出，而惩罚项的标准解代表了变换系数，下面的变分模型主要研究了含加性高斯白噪声图像去噪：

这里||·||1表示l1范数，D是一个线性变换，例如：全变差[6]、傅里叶变换、局部余弦变换、小波框架[20]等。

1.2 含泊松噪声的图像特性

假设观测图像含有泊松噪声，则

给定u和c，可得f的似然性为：

其中，ui是图像u的第i个像素值。由泊松噪声的特性可知f的期望（平均值）和方差是：

2 含泊松噪声的图像去噪

2.1 数据驱动紧框架

选择紧框架基，是因为它的多分辨率性质和冗余性质有助于算法实现和图像的稀疏表示[6-7]，基于多分辨分析（MRA）的小波由酉扩张定理[21]产生。通过小波紧框架系统的滤波器得到快速紧框架变换或分解算子W。矩阵W包括J+1个子滤波算子W0，W1，…，WJ，W0是低通滤波器，其余的是高通滤波器。通过酉扩张定理[21]，WT是快速紧框架重构算子且WTW=I，即对于任意图像均有。

最近，Cai等[19]基于输入图像的结构特征，在小波紧框架的基础上提出了数据驱动紧框架，并且该紧框架相较于小波紧框架更加精确地稀疏逼近输入图像。另外，Cai等[20]将数据驱动紧框架已经成功应用到了图像去噪中。数据驱动紧框架的设计流程具体如下：

数据驱动紧框架

输入：图像g（未污染或污染）

主程序：

2）fordo

②令 ν（k）=Tλ（W（k）g），Tλ为硬阈值算子；

④对VGT进行SVD分解，VGT=UDXT；

通过数据驱动紧框架，可以得到一组低通和高通滤波器。在此基础上，可以建立紧框架分解算子W和重构算子WT。此部分的理论由Cai等[20]提出，故具体理论在此不多赘述。

2.2 图像去噪模型和算法

根据式（1），可以得到泊松噪声的表达式如下

给定u，可得期望和方差分别为：

如果用加性高斯噪声来逼近泊松噪声ε，则ε服从正态分布 N（0，u），即

其中，∑是协方差矩阵。由噪声的独立性，可得

其中，diag（Au+c）是对角矩阵。利用极大似然性，取式（9）的负对数，得保真项

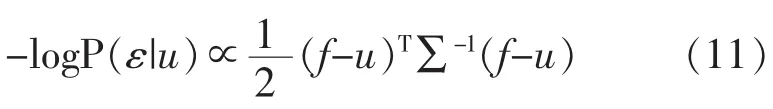
定义向量x∈RW的赋权l2范数为，Q是对称正定矩阵。那么（11）可被改写为

由于u≥0，所以∑-1是正定阵。式（12）可作为偏差原理在[22]中选择正则化参数λ，但是保真项（12）含有未知的权重u，所以需要逼近或直接解决这个非线性平方问题。例如，这个未知的权重u可以通过观测图像f逼近，即

在这个简化公式上，最小二乘方法结合正则化可以求解这个问题。

框架函数稀疏正则化和非负约束结合，得到下述图像去噪模型：

文中提出了一个基于分裂Bregman迭代[23]的新算法逼近（14）的精确解。假设存在一个迭代解uk，如果uk收敛到u*，则当k充分大时，即解决下式

随着uk逐渐稳定，1/u*逼近于1/uk，结合分裂Bregman迭代得到一个新算法，即

用算法1描述算法（16），如下：

算法1含泊松噪声的图像去噪算法

初始化：u0=0；d0=Wf；b0=0；k=1，Σ0是初始协方差矩阵；

3 数值实验

为对本文提出的去除泊松噪声的模型与算法的有效性进行验证，本小节共进行了两组数值实验，所选取的图片分别为“cameraman.tif”和“boat256.png”。在Matlab仿真平台下，通过‘poissrnd’生成泊松噪声。为了数值上强有力地说明数值实验效果，文中选取评价指标PSNR对图像去噪效果进行评价，PSNR表达式如下：

经计算得，cameraman图像（第一行）与boat256图像（第二行）的PSNR值分别为31.07、30.78。由图1和PSNR值，可以得出，本文所提的模型与算法能够有效地去除泊松噪声。

图1 cameraman图像（第一行）与boat256图像（第二行）去噪效果图

4 结论

文中首先提出了一种基于数据驱动紧框架的变分模型用于含有泊松噪声的图像去噪。然后又提出了重新赋权的分裂Bregman算法用于解该模型。本文首次完成了数据驱动紧框架与变分模型的结合，并且将所提出的模型应用到了图像去噪中。另外，数值实验表明所提出的模型与算法能够有效地进行图像去噪并且具有一定的实用性。这也说明了本文所提的模型和算法适合向其他相似研究领域推广。

[1]Csiszár I.Why least squares and maximum entropy An Axiomatic Approach to Inference for linear Inverse Problems[J].Annals of Statistics， 1991，19（4）:2032-2066.

[2]Luisier F， Blu T， Unser M.Image denoising in mixed Poisson-Gaussian niose[J].IEEE Transactions on Image Processing， 2011，20（3）:696-708.

[3]Gong Z， Shen Z， Toh K.Image restoration with mixed or unknown noises[J].SIAM Journal on Multiscale Modeling and Simulation， 2014，12（2）:458-487.

[4]Li J， Shen Z， Yin R， Zhang X.A reweightedmethod for image restoration with Poisson andmixed Poisson-Gaussian noise[J].Inverse Problems Imaging， 2015，9（3）:875-894.

[5]Staglianò A， Boccacci P， Bertero M.Analysis of an approximate model for Poisson data reconstruction and a related discrepancy principle[J].Inverse Problems， 2011， 27（12）:1061-1063.

[6]Rudin L I， Osher S， Fatemi E.Nonlinear total variation based noise removalalgorithms[J].Physica D-nonlinear Phenomena， 1992， 60（1-4）:259-268.

[7]Chambolle A，Lions P L.Image recovery via total variation minimization and related problems[J].Numerische Mathematik，1997，6（2）:167-188.

[8]Meyer Y.Oscillating Patterns in Image Processing and Nonlinear Evolution Equations:The Fifteenth Dean Jacqueline B.Lewis Memorial Lectures[J].Of University Lecture，2001（22）:122.

[9]Sapiro G.Geometric partial differential equations and image analysis[M].Cambridge University Press，2001.

[10]Osher S， Fedkiw R.Level set methods and dynamic implicit surfaces[M].Springer New York，2003.

[11]Chan T， Esedoglu S， Park F， et al.Total Variation Image Restoration:Overview and Recent Developments[M]//Handbook of Mathematical Models in Computer Vision，2006:17-31.

[12]Aubert G，Kornprobst P.Mathematical problems in image processing:partial differential equations and the calculus of variations[M].Springer Science and Business Media，2006.

[13]Yang J B，Wang C.A wavelet frame approach for removal of mixed Gaussian and impulse noise on surfaces [J].Inverse Problems and Imaging，manuscript，2016.

[14]Chan R H， Chan T F， Shen L， et al.Wavelet algorithms for high-resolution image reconstruction[J].SIAM Journal on Scientific Computing， 2002，24（4）:1408-1432.

[15]Cai J F， Osher S， Shen Z.Split Bregman methods and frame based image restoration [J].SIAM Journal on Multiscale Modeling and Simulation，2009， 8（2）:337-369.

[16]Dong B，Shen Z.MRA-based wavelet frames and applications[M].IAS Lecture Notes Series，Summer Program on The Mathematics of Image Processing[M].Park City Mathematics Institute，2010.

[17]Chan R，Shen L， Shen Z.A framelet-based approach for image inpainting[J].Res Rep，2005.

[18]Cai J F， Osher S， Shen Z.Linearized Bregman iterations for frame-based image deblurring[J].SIAM Journal on Imaging Sciences， 2010， 2（1）:226-252.

[19]CaiJ F， Shen Z.Image restorations:total variation，wavelet frames and beyond[J].Journal of the American Mathematical Society， 2012， 25（4）:1033-1089.

[20]Cai J F，Ji H，Shen Z，et al.Data-driven tight frame construction and image denoising[J].Applied and Computational Harmonic Analysis， 2013， 37（1）:89-105.

[21]RonA， ShenZ.AffineSystemsinL2（Rd）:TheAnalysis of the Analysis Operator[J].Journal of Functional Analysis， 1997， 148（2）:408-447.

[22]Bertero M， Boccacci P， Talenti G， et al.A discrepancy principle for Poisson data[J].Inverse Problems， 2010，26（10）:105004-105023.

[23]Goldstein T，Osher S.The split Bregman method for L1 regularized problems[J].SIAM Journal on Imaging Sciences， 2009，2（2）:323-343.

Application of data-driven tight frame in gray image denoising

FAN Li-jing，WANG Cong
（College of Science， Hohai University， Nanjing 211100， China）

In this paper，we proposed a data-driven tight frame based variational model for image denoising with Poisson noise，in order to remove Possion noise from noisy gray image and analyze image data further.And we proposed reweighted split Bregman algorithm to solve this model.Combining with supporting numerical experiments and PSNR indicators，we assessed the model evaluation results.Results showed that the algorithm was feasible and effective.

data-driven tight frame； Poisson noise； image denoising； split Bregman algorithm

TN919.8

：A

：1674－6236（2017）15-0180-04

2016-09-22稿件编号：201609204

国家自然科学基金项目（11101120）；中央高校基本科研业务费专项资金资助项目（2015B38014）

范立静（1990—），女，山东济宁人，硕士研究生。研究方向：小波分析及应用、图像处理。