基于特征值问题的正交小波构造方法

黄允浒，吐尔洪江·阿布都克力木，刘芳园，王 鑫，张鹏杰

（1.新疆师范大学 数学科学学院，新疆 乌鲁木齐830017；2.新疆巴音郭楞蒙古自治州和硕县高级中学 新疆 乌鲁木齐841200）

基于特征值问题的正交小波构造方法

黄允浒1，吐尔洪江·阿布都克力木1，刘芳园1，王 鑫1，张鹏杰2

（1.新疆师范大学 数学科学学院，新疆 乌鲁木齐830017；2.新疆巴音郭楞蒙古自治州和硕县高级中学 新疆 乌鲁木齐841200）

本文提出了一种基于具有高阶消失矩的IIR正交小波构造方法.从小波的正交性和正则性条件出发，可以得到一些约束IIR滤波器组的条件，并且探讨约束滤波器系数及其零极点的关系。依这些关系，可以直接将Remez算法应用于禁止带上，并制定了设计特征值问题形式的问题。其次，一组滤波器系数可以通过解它的特征值问题而容易地计算出来，并且通过施加迭代过程后将得到等波纹响应的最优滤波器系数，可以任意的指定消失矩的阶数。

正交小波；高阶消失矩；Remez算法；特征值问题；IIR滤波器

小波理论[1]是继Fourier级数基础上发展起来的另一有效信号处理工具，其目的是为了使之更适用于局部变化处理。最突出特点是多分辨率分析（MRA）特性，这种特性可以将信号进行时频局部化分析，此思想的形成又源于工程应用的推动，MRA不仅为正交小波的构造提供了一种简单方法，且为正交小波变换的快速算法提供了理论基础。同时，MRA又与多采样率滤波器组不谋而合，使小波变换同数字滤波器理论结合起来。消失矩是小波的一个重要特性,在小波分析中，由于小波变换事实上是一种具有特殊结构的完全重构滤波器，具有高阶消失矩的小波相当于一个多尺度微分算子的作用，可以揭示出函数的可微性与其在细尺度下的衰减性之间的关系，许多小波的构造方法也被提出，比如由尺度函数，B-样条函数等构造正交小波[2-6]。除了以上方法外，基于Daubechies方法也可以得到正交和双正交小波滤波器。Daubechies已经证明，同时具有紧支撑和对称性的实值正交小波仅有Haar小波，但Haar小波不具有连续性.为了得到比Haar小波滤波器更具有光滑性的实值正交对称小波滤波器，Herley和Vetterli的文献中提出了一类IIR解，并且讨论了两种情况[8]：HSS（half sample symmetric）与 WSS（whole sample symmetric）。

由完全重构二通道滤波器组的方法来得到小波基[10-11]。本文考虑一个仿酉滤波器组，它在迭代时生成正交小波基.通过IIR来实现仿酉滤波器组的应用。两个全通滤波器并联所产生的传递函数是有限的，而消失矩显示了生成的小波在时间上的平稳变化。在文献[4-5]的方法中不能用于产生具有高阶消失矩的小波基。

在本文中，基于传统的IIR滤波器的消失矩，提出构建高阶消失矩正交小波的构造方法.由于在合成正交小波基时减少了正交滤波器组的设计，所以只需考虑具有附加平坦度约束的IIR正交滤波器组的设计.由小波的正交性和正则性特点出发[13]，得到IIR滤波器组的约束条件，并研究了约束滤波器系数及其零极点之间的关系。根据这些关系，可以发现，该积滤波器的幅度响应在通带和阻带之间反对称的[16]。因此，可以直接在阻带之间运用Remez算法，并制定特征值问题的形式设计，通过得到的一组滤波器系数作为相应的特征向量，通过求解特征值问题的以计算最小绝对特征值，最后等波纹响应的最优滤波器系数可以通过迭代方法得到.为说明上述方法的有效性，以 M=N=4，K=6 与 M=5，N=4，K=8 为例验证所设计的仿酉滤波器组的正确性。

1 小波和滤波器组

正交小波基可由仿酉滤波器组来生成{H（z），G（z）}[11]，其中 H（z）是低通滤波器，G（z）是高通滤波器。

命题1 由实系数的二通道仿酉滤波器组{H（z），G（z）}能够获得实值正交小波滤波器，从小波的正交性，滤波器组H（z）和G（z）所满足的正交性条件是[1]:

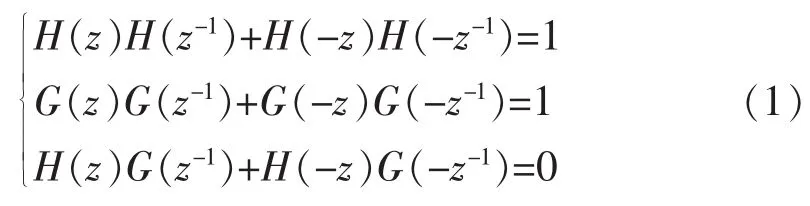
定义该滤波器

命题2 由命题1知，P（z）是半带滤波器，半带滤波器的P（z）的表示形式如下:

其中N，M是整数，滤波器系数ai和bi是实数，b0=1。注意由于N和M可以任意的选择，传递函数比一个全通滤波器更一般[3-4]。

可见，P（z）具有对称的滤波器系数，H（z）和 G（z）的零点与极点在单位圆镜像对上，分解P（z）的零点以获得一个稳定的H（z）。假设P（z）的分子和分母分别为 N（z）N（z-1）和 D（z2）D（z-2），而 P（z）的所有极点在 D（z2）单位圆内， 得到稳定的 H（z），即

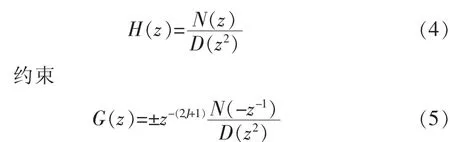
其中 J=max{N，M}。

2 IIR滤波器组的设计

2.1 性 质

在设计滤波器前，研究积滤波器P（z）的设计[13]，写成如下形式:

可以从方程（4）中得到 P（z）的幅度响应[1]，通过下式

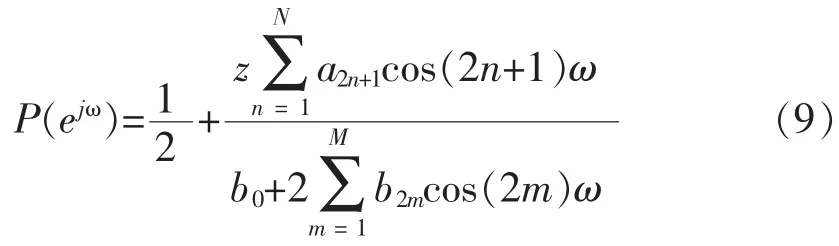
2.2 最大平坦响应滤波器

为使所获得的消失矩最大，必须设计一个最大平坦响应滤波器。因此，需要找到z=-1处的独立零点，就是 K=I2，而分子多项式 P（z）是

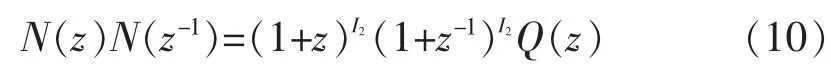
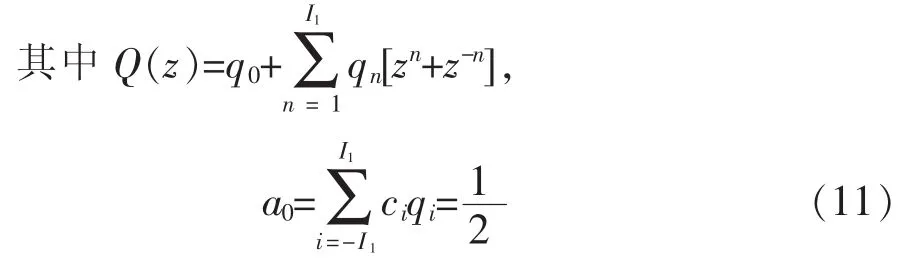
2.3 具有任意消失矩的滤波器

考虑一个在给定的连续K阶消失矩IIR滤波器具有最佳的频率。由于z=-1在处，H（z）有K重零点，而P（z）的分子多项式可以表示为

从（6）式知，P（z）共有 2I2个独立零点，而 K 必须满足 K≤I2，因此其余零点数是 2I3（I3=I2-K）。

考虑P（z）在单位圆上所有零点必须是成对的，构造出 P（ejw）如下：

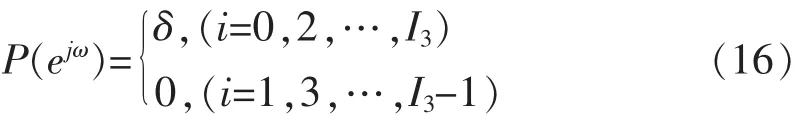
其中δ是一个幅度误差，把方程（7）和（13）代入方程（17）， 可以重新写出方程（17），（15）或（16） 式的矩阵形式：

其中 Q=[q0，q1，…，q（L-K）]T，B=[b0，b2，…，b2M]T，而 S中的元素为

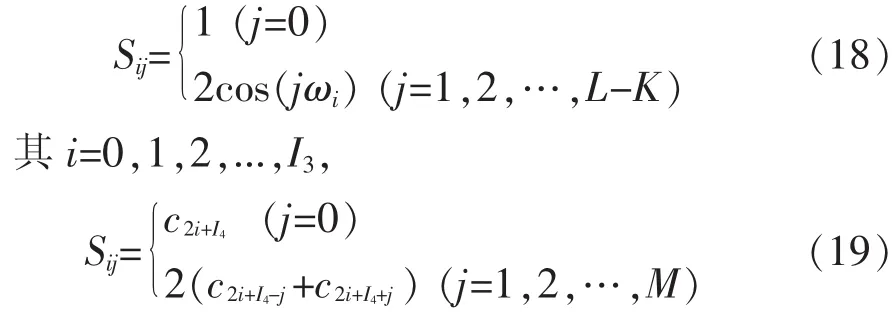
当 i=I3+1，I3+2，…，L-K，有 I4=2（M-I3）；当 N＞M时，有 I4=2（M-I3）；

当 N＜M-1，有 I4=2（N-I3）+1，注意到ci=0，

当 i＞K 时，T的元素为

当 i=0，1，2， …，M 时， 把方程（23） 代入方程（17）， 可得

这相当于一个广义特征值问题，Q为相应的特征向量。尽量减小幅度误差δ。

3 数值算例

下面采用本文方法构造相应的正交小波滤波器。

1）考虑N=M=4情况的最大平坦滤波器设计。所设计的滤波器H（z）的响应幅度具有最小相位响应。如图1实线所示，并且所生成的尺度函数和小波函数分别如图2和图3所示。在图1中，两个滤波器的幅度响应在图中也显示了N=3和M=5，或N=5，M=3；M=3也在图中显示。认为在图1中，3个滤波器的幅度响应基本相同，这是因为在ω=0和ω=π时，这3种滤波器有相同的平坦度。

采用本文的方法验证N=M=4（N=3和M=5情况类似）时大平坦滤波器设计。

首先令 N=M=4，K=6，ws=0.6π

则 L=max{2M，2N+1}=9，

I1=L-M-N-1=0， I2=N+M+1=9，

I3=I2-K=3， I4=2（M-I3）=2，

由于，

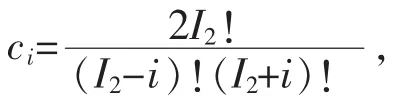
N1=min{I1，I2-n}=0；

N2=min{L-K，K-n}=-3；

N3=min{L-K，K+n}=3。

经计算有:c0=5.5114638448e-06，

c1=4.9603174603e-06，c2=3.60750360751e-06，

c3=2.1043771044e-06，c4=9.71250971251e-07，

c5=3.4687534687e-07，c6=9.250009250e-08，

c7=1.7343767343e-08，c8=2.0404432169e-09。

在阻带等间隔选取频率的初始值 Ωi，（0≤Is≤I3），（i=0，1，…，I3）。 令 ωi=Ωi；

由（18）式得到

由（20）式得到

对（TV）-1S做特征分解，有特征值

q0=0.755732626；q1=0.37825879；

q2=0.37820973；q3=0.3778182526。

及特征向量

Q=[0.755732626 0.37825879 0.37820973 0.377818]T

且由（6）式和（13）式 ，可得

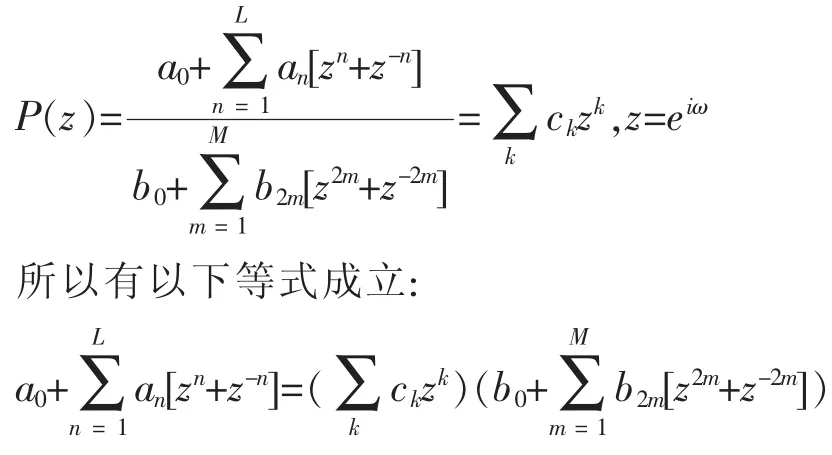
所以比较等式两端同次幂项的系数得到a0，a1，a2，a3，…，a8

综上又有 P（z）满 P（z）=H（z）H（z-1），

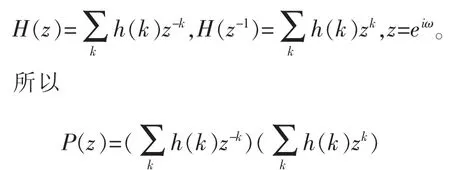
得到低通滤波器系数h（k）=[h（-4），h（-3），h（-2），…，h（1），h（2），h（3），h（4）]；由低通滤波器系数与高通滤波器系数关系g（k）=（-1）1-kh（1-k），得到高通滤波器系数g（k）。进而得具有高阶消失矩的正交小波。

图1 例1）的归一化频谱图

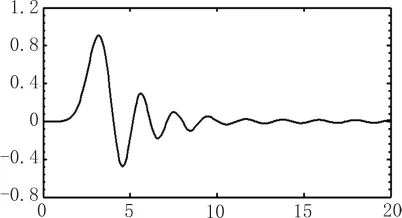
图2 例 2）的尺度函数 φ（t）

2） 考虑 N=4，M=5，K=8 和ws=0.6π 的仿酉滤波器组的设计。使用上述的积滤波器并构造H（z）和G（z）具有最小相位响应，H（z）的幅度响应示于图4中的实线，而产生的尺度函数和小波函数分别如图5和6所示。在图4中K=6或K=10的两个幅度也在图中显示。很显然减小K时，幅度误差将减小。

4 结论

文中提出了一种新的构造高阶消失矩正交小波基方法，从小波的正交性和正则性出发得出IIR仿酉滤波器的一些制约因素，并研究了约束滤波器系数与零极点之间的关系，可以在带阻中直接利用Remez算法，并制定了设计特征值形式问题.通过求解特征值，可以得到一组滤波器系数作为相应的特征向量.因此与等波纹响应的最优滤波器系数可以容易地从施加迭代过程后得到。在计算上，本文的方法是有效的，可以任意的指定小波消失矩的阶数。

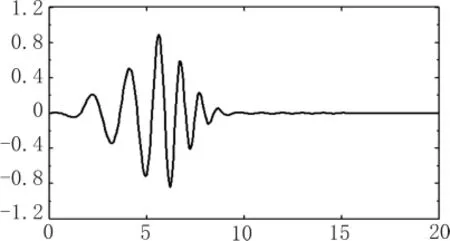
图3 例 1）的小波函数ψ（t）

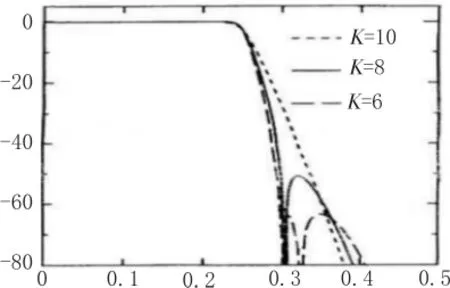
图4 例2）幅值响应

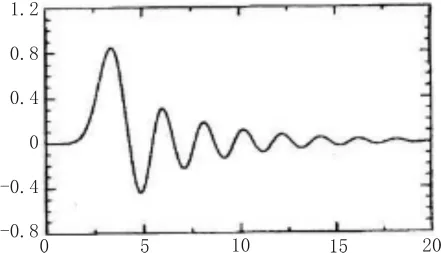
图5 例 2）的尺度函数 φ（t）

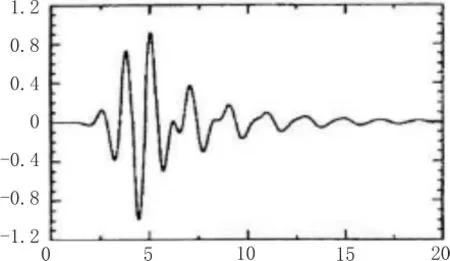
图6 例 2）的小波函数ψ（t）

[1]吐尔洪江·阿布都克力木.小波信号处理基础[M].北京：北京邮电大学出版社，2014.

[2]IngleV K，Proakis J G.数字信号处理[M].MATLAB版.刘树棠，陈志刚，译.西安:西安交通大学出版社，2013.

[3]杜勇.数字滤波器的MATLAB与FP-GA实现[M].2版.北京:电子工出版社，2014.

[4]周建峰.三元双正交小波滤波器组的刻画[J].数学的实践与认识， 2014， 44（3）:134-141.

[5]韩芳芳，段发阶，张宝峰.偶数长有理数对称紧支双正交小波滤波器的设计 [J].计算机工程与应用， 2010， 46（31）:10-13.

[6]任燕，郭仓库.基于改进复扩散耦合非局部均值滤波器的图像放大 [J].系统工程与电子技术，2016，38（5）:1182-1187.

[7]曲怀敬，李 健，吴延荣.结合滤波器选择和相位信息的统计纹理图像检索[J].计算机应用研究，31（12）:3894-3897.

[8]张爱玲，何培栋，潘洪刚.电控可调谐的正交偏振双波长滤波器的设计 [J].激光与光电子学进展2015，072-301:1-3.

[9]刘虔，彭力，唐诗颖.一种基于图解的LCL滤波器设计和优化方法[J].中国电机工程学报，2012，32（36）:36-40.

[10]Abdukirim T， Abulikemu A， ZHANG Haiying.Lifting Dyadic W -avelets and Design of Decomposition on Filters with Short Length[C]//IEEE International Conference on Computer and Automation Engineering， 2011（1）:517-520.

[11]Abdukirim T，ROZI A.Design of dyanic wavelet filters with vanishing moments using dyanic lifting Sche-.Me[C]//IEEE International Conference on Intelligent Computingand IntelligentSystems，2011（3）:219-223.

[12]杨爱萍，张金霞，刘建忠，等.紧支撑等偶长度双正交小波滤波器组设计 [J].计算机工程与应用，2012，48（3）:89-92.

[13]陈星东，谢依部力·赛依都力，阿不米提·肉孜.IIR实值正交对称小波滤波器的设计 [J].科技信息（博士·专家论坛）， 2011：436-438.

[14]时伟，陈建群.基于区间正交小波变换的多尺度实时Kalman滤波器设计[J].中南大学学报：自然科学版，2011，42（9）:2712-2715.

[15]李飞，张兴，朱虹.一种LCLLC滤波器及其参数设计[J].中国电机工程学报，2015，35（8）:2009-2016.

[16]张小燕；吐尔洪江·阿布都克力木，冯惠，等.基于卷积型正交条件的小波构造方法[J].新疆师范大学学报：自然科学版，2015，34（4）:47.

The method of orthogonal wavelet construction based on eigenvalue problem

HUANG Yun-hu1，Turghunjan AbdukirimTurki1，LIU Fang-yuan1，WANG Xin1， ZHANG Peng-jie2
（1.College of Mathematical Sciences， Xinjiang Normal University，Urumqi 830017， China；2.Xinjiang Bayinguoleng County of Mongolia Autonomous Prefecture of Xinjiang High School， Urumqi 841200，China）

This paper presents a method of IIR orthogonal wavelet construction method based on high order vanishing moments.Starting from the wavelet orthogonality and regularity conditions，we can get some constrained IIR filter group，and to explore the relationship between the filter coefficients and zero pole constraints.According to these relations，can be directly applied Remez algorithm to the forbidden to take on， and the design form of eigenvalue problem problem.Secondly， a set of filter coefficients by solving its eigenvalue problem and easily calculated，and by applying the iterative process will get the best response of corrugated filter coefficients，specify the number of vanishing moments can be arbitrary.

orthogonal wavelet； high order vanishing moments； Remez algorithm； eigenvalue problem；IIR filter

TN8；TN97

：A

：1674－6236（2017）15-0001-05

2016-10-12稿件编号：201610058

国家自然科学基金资助项目（11261061；61362039；10661010）；新疆维吾尔自治区自然科学基金资助项目（200721104）；新疆师范大学研究生科技创新项目基金资助（XSY201602010）

黄允浒（1990—），男，福建泉州人，硕士研究生。研究方向：小波分析及其图像处理。