基于视频图像技术的简支梁动静载试验分析
2017-09-03任张晨袁向荣董湘婉徐旻杰
任张晨, 袁向荣, 董湘婉, 徐旻杰
(广州大学 土木工程学院, 广东 广州 510006)
基于视频图像技术的简支梁动静载试验分析
任张晨, 袁向荣, 董湘婉, 徐旻杰
(广州大学 土木工程学院, 广东 广州 510006)
采用视频图像技术对带传感器和不带传感器的简支梁的振动进行模态分析,采用Matlab软件把简支梁的振动视频分解成图像,对分解得到的图像裁剪出感兴趣区域并进行灰度化和二值化处理。为了精确,对得到的整像素边缘进行了亚像素化处理,得到梁下边缘的亚像素级别的时域信号,对这些信号数据进行模态分析得出前三阶频率和振型,并与Midas建立的有限元模型、传统的动载试验处理得到的结果三者相比对,对比表明,基于视频图像技术的动静载检测有更高的精度和可操作性,可以弥补传统检测的不足。
简支梁; 动静载检测; 模态分析; 视频图像技术
结构的振动特性是判断桥梁结构承载能力和运营状况的重要指标,动载试验[1]和静载试验[2-3]为传统检测中最典型的两种检测方式。简支梁是最常见的结构形式,对简支梁的振动测试及了解简支梁的振动特性在结构的安全评估和测试中具有重要意义。传统的动静载试验都有共同的不足之处:由于传统的检测都需要采集整个桥中的部分测点的振动数据,所以检测结果受到测点的影响,测点过多则不经济,测点过少结果不准确。本文采用视频图像技术对简支梁进行动静载试验研究,视频图像检测具有全尺度测量、精度高、操作性强等重要优势,可以避免传统检测受测点的制约。各种边缘检测算子[4]的出现不断地推动着数字图像技术的发展。经典算子如Laplace算子[5]、Canny算子[6-7]、Sobel算子、Roberts算子、Log算子等,这些算子具有计算速度快、边缘识别精度高、重复可比性好等优势。
模态分析[8-9]的目的是识别结构振动时的模态参数[10],在现代桥梁振动分析中的应用十分广泛。刘辉[11]仅对五等跨连续梁采用DASP系统[12-13]进行了模态分析,但没有采用视频图像法对比论证。因此,本文对简支梁也进行传统的动静载试验得到振动结果,再和有限元模型分析结果以及视频图像分析的结果相对比,来论证视频检测技术的精确性和可靠性。
1 基于视频图像法的静载试验
试验梁总长2.05 m,质量为331 g,均布质量ρA=0.16 kg/m。左端采用砝码加重,视为固定铰支座;右端采用钢辊轴作为支承方式,构成活动支座。支座距离为1.9 m。试验模型见图1,简图见图2。

图1 简支梁试验模型图
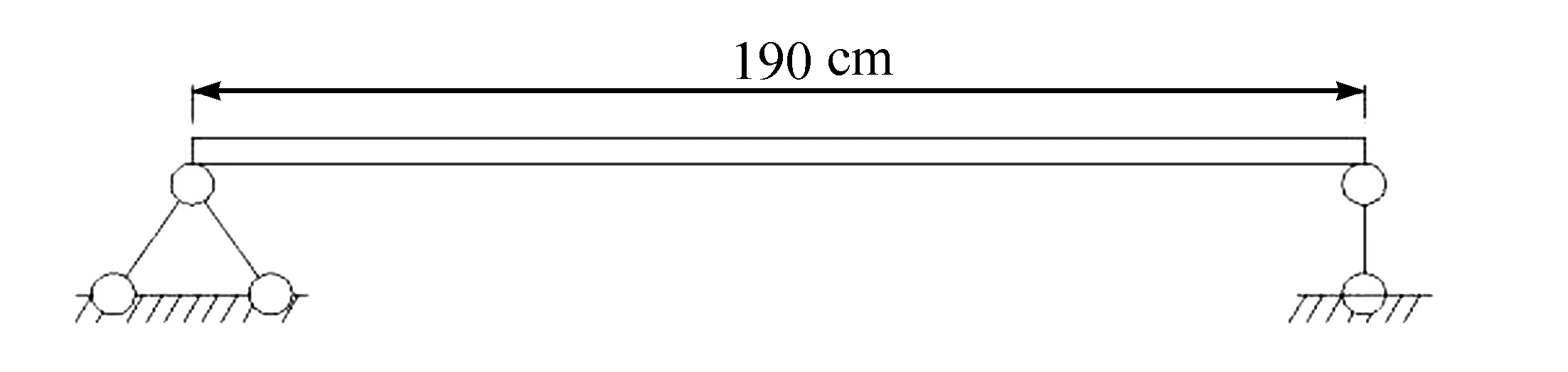
图2 简支梁试验模型简图
采用视频法对该简支梁的抗弯刚度EI进行静载试验并计算。
首先在静止的简支梁上依次加上质量为100 g的小砝码,一共加至400 g,待其静止时分别拍下照片,并最后在一张照片中拍下钢尺,作为接下来计算挠度的计算参考。施加砝码后的简支梁图见图3。

图3 施加砝码后简支梁的位置图
采用Matlab软件中的imread和imtool工具将拍摄照片读入和显示,并记录下边缘跨中位置点的像素边缘坐标位置,见表1。
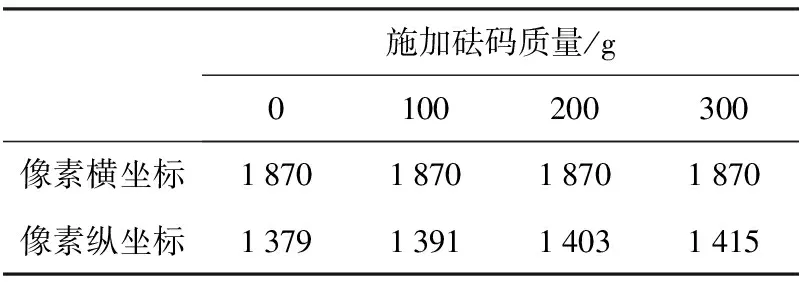
表1 施加砝码后简支梁下边缘跨中位置的像素坐标
由表1数据可知,每施加100 g砝码,梁下边缘跨中位置的像素纵坐标就增加12。试验中拍下钢尺1 cm在照片中像素纵坐标差为16。因此像素纵坐标差12表示实际长为12/16=0.75 cm。
简支梁在受集中力下的挠度公式为
(1)
式中:l为计算跨径,p为集中力,EI为抗弯刚度,Ymax=0.075 cm。
代入数据计算得:
EI=18.67N·m2
角频率ωn公式为
(2)
式中:ρA为均布质量,EI为抗弯刚度,n为阶数。
由ωn=2πf得到该简支梁的前三阶固有频率见表2。
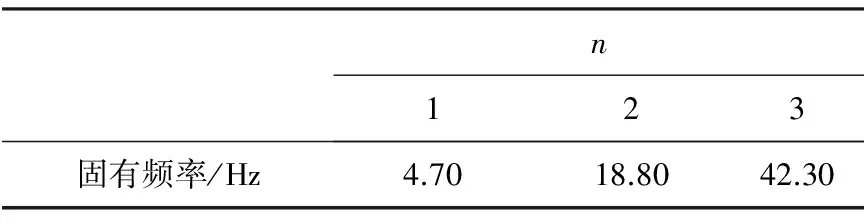
表2 简支梁静载试验的前三阶固有频率理论值
2 传统的动载试验
2.1 传统检测的动载试验模型
用卷尺将试验梁每跨均分为5份,在均分点上分别放置加速度传感器(选用BI1148加速度传感器),并连接信号采集仪(使用的是INV306U信号采集处理分析仪),传感器布置图见图4。模型简图见图5。

图4 传统检测的试验图
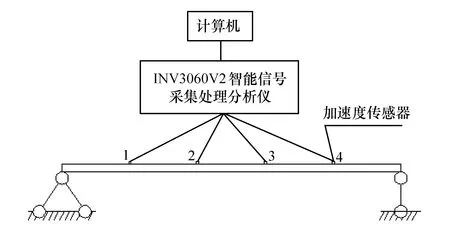
图5 传统检测的试验模型简图
2.2 传统检测的动载试验结果
激振方法采用锤击法。振动信号经采集仪采集结束后,以测点1为参考点,分别对4个测点进行传递函数分析,将这4个测点得到的数据进行模态分析。使用频域法定阶和复模态多自由度拟合便可得到该简支梁的前三阶频率(见表3)及振型(见图6)。
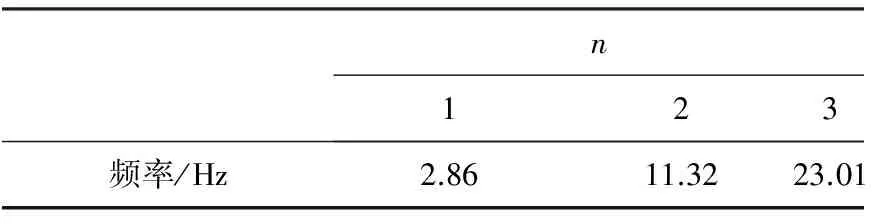
表3 传统检测法实测前三阶频率

图6 传统检测法实测动载试验的前三阶振型图
3 基于视频图像法的动载试验
3.1 视频图象法处理流程
为了追求一致性,视频图像法的动载试验共进行带传感器和无传感器的简支梁动载试验。同前文一样,对简支梁进行锤击,通过相机采集到简支梁振动的整个过程,然后采用Matlab软件对振动视屏进行处理。
现以带传感器的简支梁动载试验的处理流程为例做说明如下:
读取视屏,并将视屏分解成彩色图片。本实验一共录制视屏时长18 s,录制帧数为120帧/s,即一共剪裁到2 255张彩色图片。随后将彩色图片转成灰度图像并剪裁感兴趣区域。选取(1)—(3)序列作为演示,如图7所示。
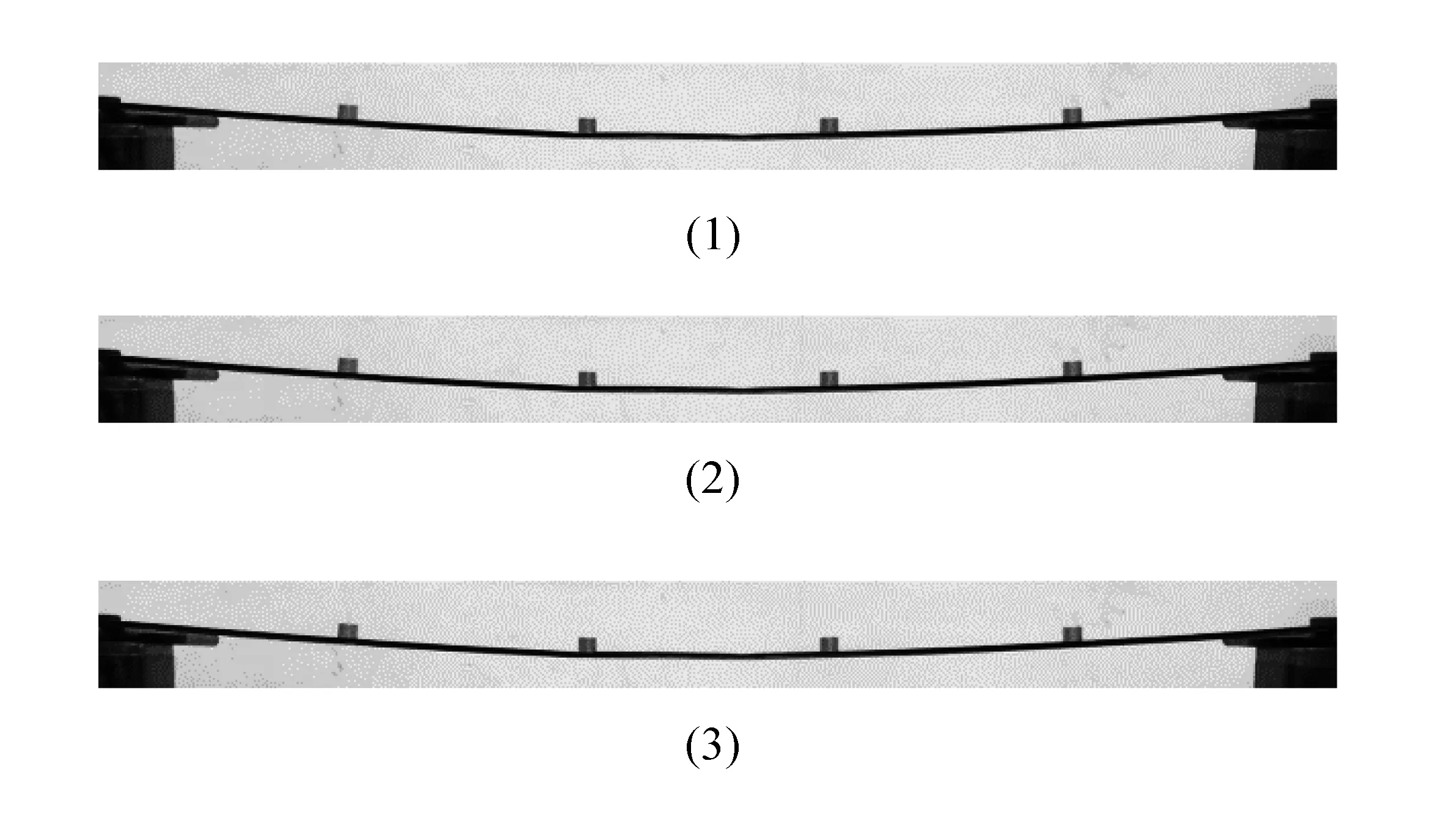
图7 简支梁振动的灰度图像
得到灰度图像后,设定合适的阈值并采用canny算子对边缘进行识别,将灰度图像二值化得到黑白图像。选取(1)—(3)序列对应的黑白图像作为演示,如图8所示。

图8 简支梁振动的黑白图像
但是上面得到的边缘位置的精度只精确到一个像素,有较大的误差。为了更精确,本文使用了多项式拟合程序对每幅二值图的下边缘进行亚像素边缘检测,检测的精度达到0.01个像素,便可确定各时刻梁亚像素边缘位置和各点的时程曲线。以1/5位置下边缘的时程曲线为例,如图9所示。

图9 梁1/5位置下边缘的时程曲线
最后对上述得到的信号数据进行模态分析便可得到视频实测的简支梁(带传感器)的前三阶振型及频率。
3.2 视频图像法动载试验处理结果
视频图像法的动载试验检测到的简支梁(带传感器)的前三阶频率见表4,前三阶振型图见图10。对简支梁(无传感器)进行同上述一样的动载试验并重复上述视频图像处理步骤,得到相应的灰度图像、黑白图像及各时刻亚像素边缘的时间历程。最后得到的简支梁(无传感器)的前三阶频率见表5。
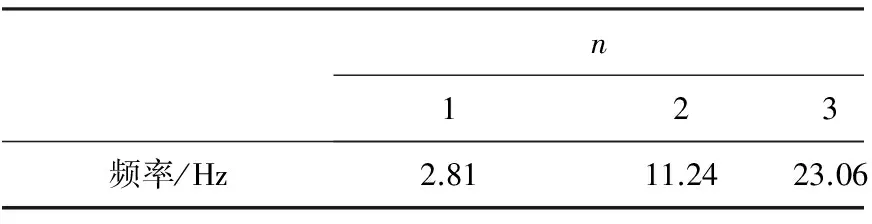
表4 视频法动载检测的简支梁(带传感器)前三阶频率
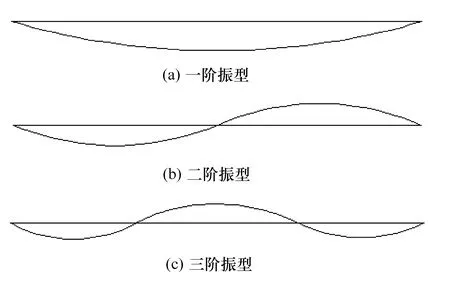
图10 视频法动载检测的简支梁(带传感器)的前三阶振型图
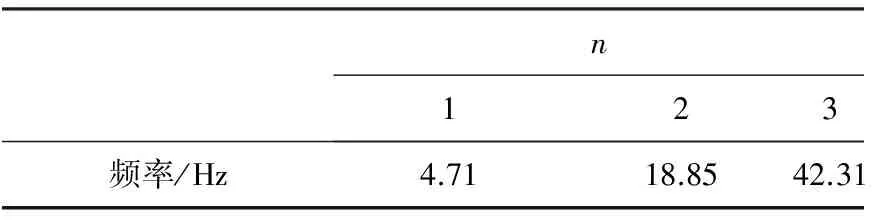
表5 视频法动载检测的简支梁(无传感器)前三阶频率
4 简支梁的有限元模态分析
4.1 建立有限元模型
使用Midas Civil有限元软件建立带传感器简支梁和无传感器简支梁两组有限元模型,并对空间梁单元进行单元划分和约束处理。其中在对带传感器简支梁的模型建立时,在传感器相应的每个位置即5分点上都加上一个集中力,这个力的大小即为传感器的重力G:G=mg=0.112×9.8=1.1N。最终建成的简支梁(带传感器)有限元模型见图11。
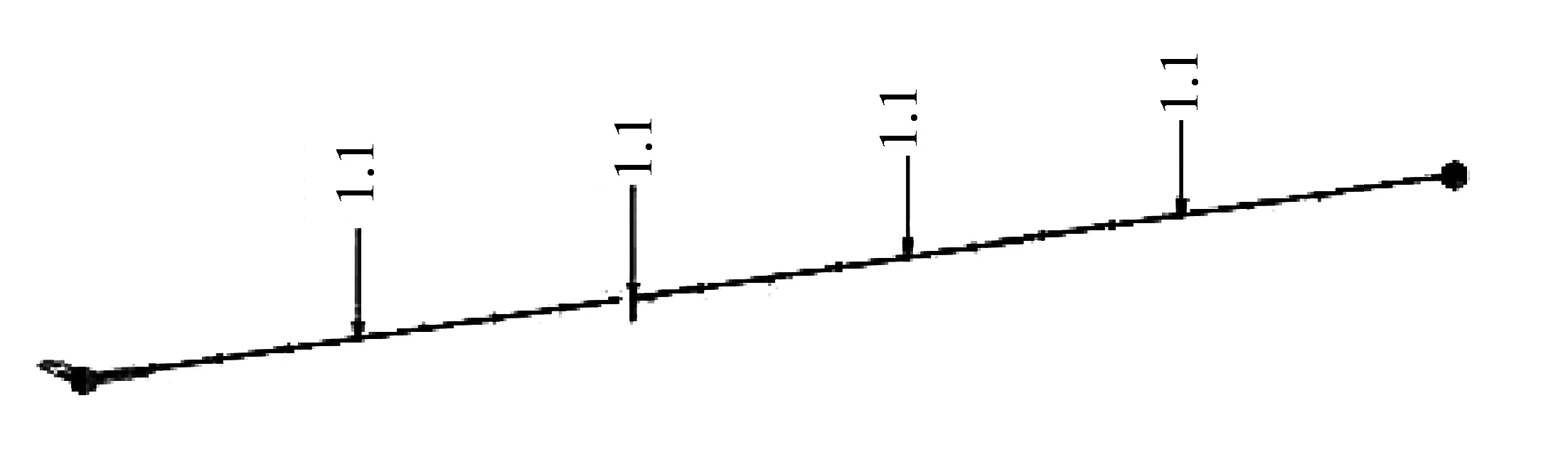
图11 简支梁(带传感器)的有限元模型
4.2 有限元分析结果
通过有限元计算得到了两组简支梁模型的前三阶振型和频率,固有频率分别见表6和表7,简支梁(带传感器)的前三阶振型图见图12。
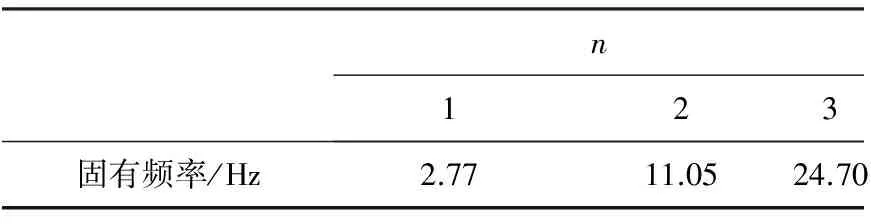
表6 有限元分析的简支梁(带传感器)前三阶固有频率

表7 有限元分析的简支梁(无传感器)前三阶固有频率
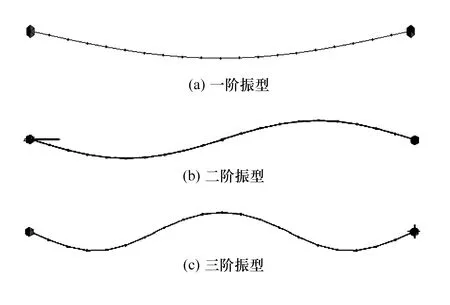
图12 简支梁(带传感器)的有限元分析前三阶振型图
5 3种方法的动静载试验结果对比分析
将有限元和视频图象法对简支梁(无传感器)的分析计算结果汇总至表8;有限元、传统试验和视频图象法的试验对简支梁(带传感器)的分析计算结果汇总至表9。
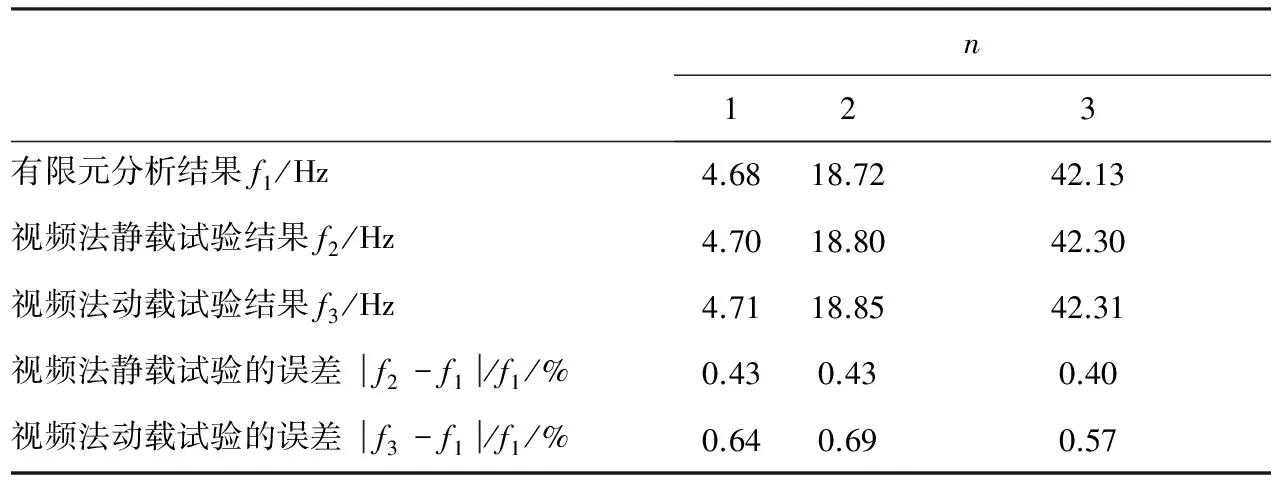
表8 简支梁(无传感器)试验频率汇总
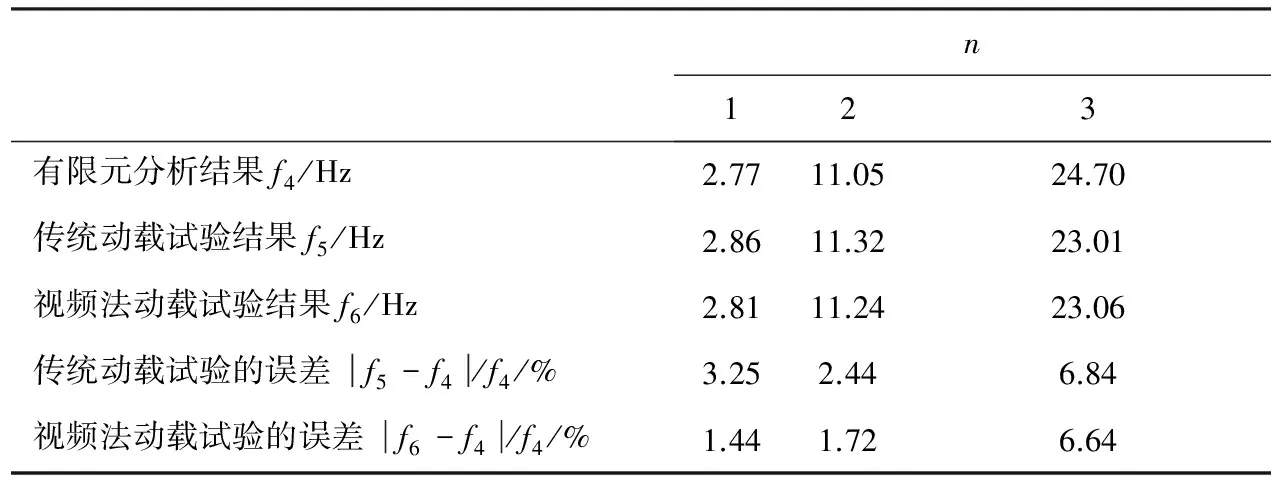
表9 简支梁(带传感器)试验频率汇总
以上数据表明,无论传统的动载试验或是基于视频图像技术的动静载试验得到的计算误差均很小,其中不带传感器的简支梁的检测更为精确,前三阶的误差均在1%以内;对于加上传感器之后的简支梁的动静载试验,一阶二阶频率误差均比较小,最大的仅为3.25%,三阶频率的误差均稍大一些,分别为6.84%和6.64%,主要原因是梁板比较宽薄,加上4个传感器后的质量远比试验梁本身的质量大的多,导致高阶振型误差比前两阶的稍大些,但误差都在允许范围之内。总体看来,基于视频图像法的动静载检测有更高的精确性和可行性。
6 结论
通过有限元计算、传统动载试验和视频法的动静载试验的对比分析,可以得到以下结论:
(1) 传统检测和视频检测所得的结果误差均比较小。从误差看,视频检测比传统加速度传感器检测更精确,每阶的误差都比传统检测小。因此基于视频图像的边缘检测技术是可行的,精度和可行性均较高。
(2) 与传统检测相比,基于视频图像法的动载静载试验无需接触,且具有更好的全局性、操作性、经济性、方便性等优势。
(3) 采用亚像素边缘检测技术对于边缘位置的确定具有更高的精度。
(4) 采用视频图像技术可以方便地计算连续梁桥的各阶模态参数,可为了解结构的振动特性提供重要的参考依据。
References)
[1] 张兰英. 桥梁动载试验的作用与发展前景[J].公路,2002(9):32-35.
[2] 吴建奇,郑晓,张婷婷. 桥梁检测中的静载试验研究[J].铁道建筑,2001(2):42-44.
[3] 吴永毅. 基于动静载试验的桥梁状态评估初探[D].广州:华南理工大学,2013:25-39.
[4] 赵芳,栾晓明,孙越. 数字图像几种边缘检测算子检测比较分析[J].自动化技术与应用,2009,28(3):48-50.
[5] 野媛. 图像边缘检测Laplace模板的改进[J].办公自动化,2009(18):27-28.
[6] 周超. 边缘检测Canny算子的研究与改进[D].重庆:重庆师范大学,2012(4):10-19.
[7] 薛武,张永生,董广军,等. Canny算子子像素边缘检测方法[J].遥感信息,2013,28(1):8-10,15.
[8] 梁君,赵登峰. 模态分析方法综述[J].现代制造工程,2006(8):139-141.
[9] 龙英,滕召金,赵福水. 有限元模态分析现状与发展趋势[J].湖南农机,2009,36(4):27-28,45.
[10] 徐敏. 桥梁结构模态参数识别研究[D]. 成都:西南交通大学,2010:51-72.
[11] 刘辉,袁向荣,蔡卡宏,等. 五等跨连续梁模态分析试验及冲击系数[J].实验室研究与探索,2016,35(5):10-13.
[12] 袁海英,陈光.DASP技术在现代测试仪器平台中的应用[J].电子测量与仪器学报.2007(1):53-56.
[13] 徐文锋,袁向荣. DASP系统在连续梁模态分析中的应用[J].工程与试验,2012,51(4):58-89,76.
Analysis on dynamic and static load tests of simply-supported beam based on video image technology
Ren Zhangchen, Yuan Xiangrong, Don Xiangwan, Xu Minjie
(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)
A modal analysis is carried out on the vibration of the simply-supported beam with sensors and without sensors by using the new video image technology. The vibration video of simply-supported beam is decomposed into the image by using Matlab software, and the decomposed image is cut out into the region of interest which is processed by graying and binaryzing. In order to be accurate, the acquired whole pixel edge is processed by the sub-pixel, and the sub-pixel time-domain signal is obtained at the lower edge of the beam. The modal analysis of these signal data is carried out to obtain the first three orders of frequencies and vibration forms, which is compared with the finite element model established by Midas and the results obtained by the traditional dynamic load test. After the comparison of the two groups of experiments, the dynamic and static load tests based on video image technology have higher precision and maneuverability than the traditional detection, and it can make up for the shortcomings of the traditional detection.
simply-supported beam; dynamic and static load tests; modal analysis; video image technology
10.16791/j.cnki.sjg.2017.08.010
2017-02-21 修改日期:2017-03-31
国家自然科学基金项目(51278137)
任张晨(1993—),男,江苏南通,硕士研究生,研究方向为桥梁检测工程、数字图像技术E-mail:782818655@qq.com
袁向荣(1957—),男,河北故城,博士,教授,硕士生导师,研究方向为桥梁工程分析计算检测、结构动力学分析与测试、数字图像处理.E-mail:rongxyuan@163.com
U441.3
A
1002-4956(2017)08-0033-05
