关注平面向量数量积推导公式与定理的价值

章亚棋

(浙江省温州市龙湾区永强中学高二(6)班，浙江 温州 325024)

关注平面向量数量积推导公式与定理的价值

章亚棋

(浙江省温州市龙湾区永强中学高二(6)班，浙江 温州 325024)

平面向量数量积a·b是一个非常重要的概念，利用它可以容易地证明平面几何的许多命题，例如勾股定理、正方形的对角线垂直平分等.当然平面向量数量积关于三角形、圆甚至不等式中的一些公式与定理，可谓向量是沟通代数、几何与三角函数的一种有力工具，有着极其丰富的实际背景，在数学和物理学科中具有广泛的应用.

平面向量数量积；定理；推导与应用

平面向量的数量积是一个涉及长度与角度的一个重要概念，利用它可以证明得到许多性质、定理与公式.下面就与读者来感受平面向量数量积在平时数学学习中带来的益处.

一、应用平面向量数量积推导三角公式

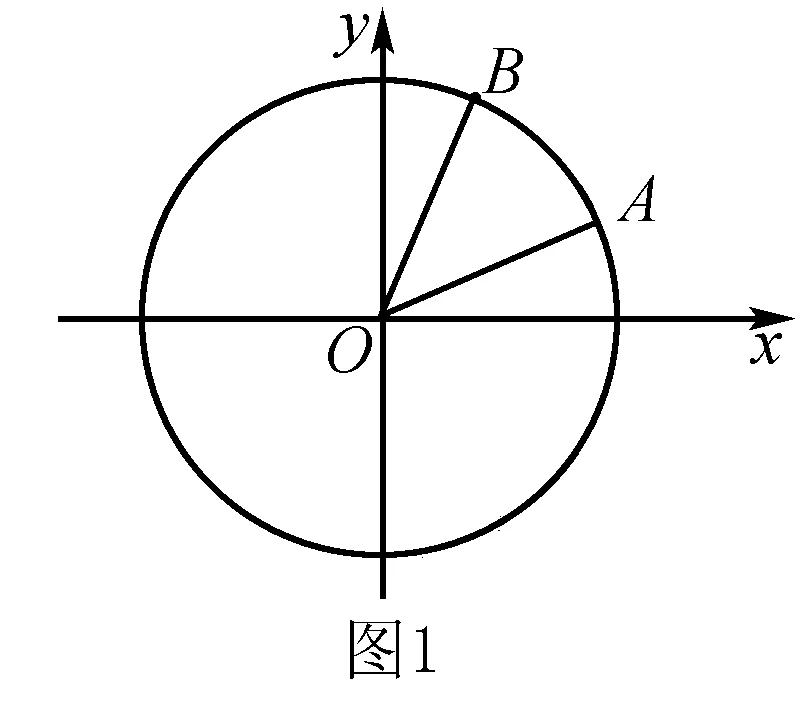
在我们的教材必修4第108页中有一个习题：如图2，在平面直角坐标系中，以原点为圆心，单位长度为半径的圆上有两点A(cosα,sinα),B(cosβ,sinβ)，试用A,B两点的坐标表示∠AOB的余弦值.

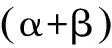
其它三角恒等变换公式都可以类似推导，这样一来不仅知道这些三角恒等变换公式是怎么来的，而且更加能领悟向量是沟通三角函数的一种工具.

二、应用平面向量数量积推导正弦定理

教材必修5中的余弦定理也是由平面向量的数量积推导出来的，后来我发现运用平面向量的数量积也可以推导正弦定理.过程如下：

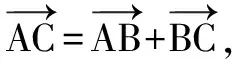
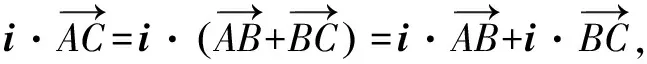
通过这里的证明再一次体会，如果涉及边长与角度问题，我们可以考虑用向量的数量积.

三、应用平面向量数量积推导柯西不等式

同样在我们的教材必修4第108页中有一个习题：

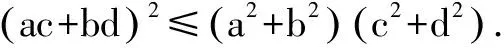
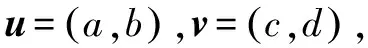
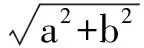
应用1 (2014年浙江高考题)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1，则a的最大值是 .

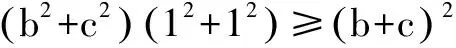
在我们平时的很多练习中，有的时候多用柯西不等式能使题目简单很多.因此我觉得平面向量数量积的贡献是巨大的，在推导很多数学的性质与结论时，很快也很有效.

四、平面向量数量积在极化恒等式的应用

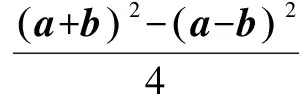
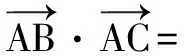
最后，我想用教材有句话作为总结：“涉及长度、角度问题常常考虑向量的数量积.”我想这句话如果我们能够深刻理解并在解题中得以灵活应用，那么我们的收获肯定很大.有了以上这些内容的印证，接下来我们在具体题目中应对平面向量的数量积要有足够的认识与应用.

[1]人民教育出版社等.普通高中课程标准实验教科书数学5必修教师教学用书[M].北京：人民教育出版社，2004.

[责任编辑：杨惠民]

章亚棋(2000.07-)，女，浙江温州人，现为温州市龙湾区永强中学学生.

G632

B

1008-0333(2017)19-0057-02