高中数学中的立体几何解题技巧
2017-09-03吉缪明
吉缪明
(无锡市第三高级中学,江苏 无锡 214000)
高中数学中的立体几何解题技巧
吉缪明
(无锡市第三高级中学,江苏 无锡 214000)
立体几何是高中数学难点和重点之一,作为需要空间思维的立体几何,我们对几何图形的认识、处理及选择正确思维方法直接决定了学生基础知识的掌握程度和应用水平.本文中笔者基于自身多年的教学经验,总结分析了立体几何解决技巧,以供同仁参考.
立体几何;解题;技巧
立体几何是高中数学知识中的重点内容,同时也是高考数学试卷中的一大难点,在高考试卷中占有较大比重的分值.在一般的练习或者考试中,由于立体几何知识本身的特殊性、多变性以及学生自身数学逻辑的不足性,解决题目方法的单一性,最终导致学生在解决题目时出现大量的错误,失去了很高的分值.其实针对立体几何的相关习题,不是一味的枯燥的计算,立体几何也有其相关的解题技巧和解题方法.
一、借助辅助,实现题目简单化
构造辅助线是在立体几何中常会出现的解题方法,也是最有效、最简便的一种解题方法.通过构造辅助线,可以使原来的立体几何的图形变得更加清晰,更加条理分明,题目的解决相较来说也会更加的容易.
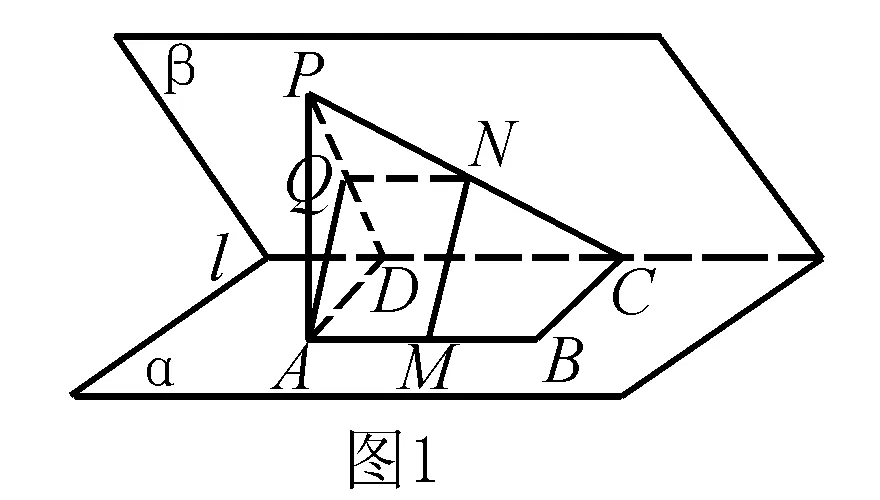
例如,如右图所示,有一二面角α-l-β,其中A、B∈α,D∈l,P∈β,PA⊥α,且PA=PD,ABCD是一个矩形,M,N分别是AB,PC的中点,证明:MN是异面直线AB和PC的公垂线.
分析 对于这道题目,看到题目的已知后,我们就能够知道仅靠题目的已知是无法进行结论的证明的,要想实现结论的证明,就必须添加适当的辅助线,借助辅助线,实现结论的证明.根据题目给出的已知:M,N分别是AB,PC的中点,我们可以考虑“利用中点,连接中位线”的方法实现证明.针对这道题目,我们就可以选取PD的中点Q(如图所示),然后连接QN、QA,于是QN就是三角形的中位线,由题目给出的已知,得出AM∥DC,于是接下来就可以根据题目的已知进一步地实现题目的证明.通过已知,加上辅助线实现题目的最终证明,这样的解题技巧是我们应当掌握的.
二、转换观念,实现解题快速化
针对立体几何来说,对于其中的一些特殊的问题,如求最值问题或者运动变化问题等,可以通过转换思想观念的方法实现题目的解决.
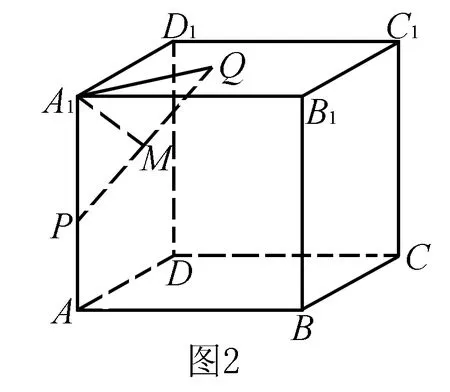
例如,如图所示,有一正方体ABCD——A′B′C′D′,其棱长为2,已知长度为2的线段PQ满足:P在正方体的AA′棱上,Q在面A′B′C′D′内,那么问PQ的中点M的轨迹的面积是多少?
分析 针对这道题,这是一道动点问题,我们要抓住问题的关键和题目的已知,仔细的进行分析,对于题目中给出的已知“P在正方体的AA′棱上,Q在面内”我们可以分析出无论线段PQ在什么位置,都有PA′⊥A′Q,然后再根据三角形的性质“斜边上的中线等于斜边的一半”就可以实现全部已知条件的利用,于是接下来的题目的解决就变得简单了.在这道题目中,我们通过将题目中PQ=2的这一定长转换为了MA=l的这一定长,实现了题目的解决.在立体几何中,经常有多种类似的问题,我们只要掌握好转换的思想,巧妙地应用解题观念的转换,那么就可以显著提高解题的速度.
三、巧设未知,实现计算简便化
针对立体几何的计算,有一个实现计算简便化的方法,就是根据题目设置未知数,然后利用未知数构建相关的算式与方程,最终通过未知数使得计算方法能够进行化简,最终实现题目的具体解决.
例如,如图所示,有一个正四棱台,其上、下底面面积分别为Q1,Q2,侧面积是Q,试求其中一个对角面的面积.

分析 对于这道题,题目中给出的已知非常的少,只有三个计算的数据,但是要求解其中的一个对角面,需要的条件比较多,如何才能够简单的进行计算呢?这时,就可以采用“设而不求”的计算方法,通过在题目中构造参数,然后实现题目的求解.我们可以设出需要的已知量,设上下底面的边长分别为a,b,斜高是l,棱台的高是h,于是对角面的计算应该是:
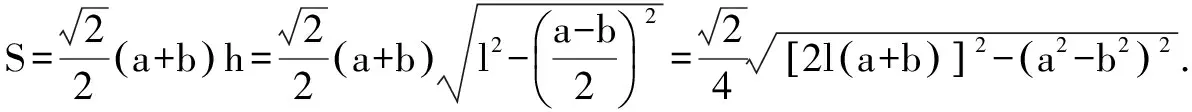
总而言之,针对立体几何的解题来说,我们面对题目时应当不慌不忙,不骄不躁,静下心来仔细地读每一道习题,认真审题,找出题目中给出的已知,认真地进行分析,选择合适的解题方法技巧:设而不求,做辅助线,转换思想等,最终实现题目的轻松解决.
[1]江士彦. 刍议高中数学中的立体几何解题技巧[J]. 读与写(教育教学刊),2015(11):99+134.
[2]杨国锋. 对立体几何试题的一些分析和思考[J]. 数学学习与研究,2015(16).
[3]何豪明,陈朝阳. 立体几何学习策略[J]. 中小学数学(高中版),2015(04).
[4]许卫华. 高中数学立体几何教学策略分析[J]. 数理化学习,2014(03).
[责任编辑:杨惠民]
2017-06-01
吉缪明(1978-)男,江苏无锡人,本科,中学一级,主要从事高中数学教学与研究.
G632
B
1008-0333(2017)19-0018-02
