例析二项式定理的应用

2017-09-03杜和平

数理化解题研究 2017年19期

关键词：展开式二项式换元

杜和平

(江苏省如皋市长江高级中学,江苏南通 226500)

例析二项式定理的应用

杜和平

(江苏省如皋市长江高级中学,江苏南通 226500)

二项式定理是高中数学中一个重要内容，二项式定理应用非常广泛.本文将给出二项式定理的几个应用.

高中数学；二项式定理；利用

1.利用二项式定理求代数式的值

A.2 B.0 C.-1 D.-2

点评多项式乘法的进位规则.在求系数过程中，尽量先化简，降底数的运算级别，尽量化成加减运算，运算过程可以适当注意赋值法的运用，例如求常数项，可令x=0；求系数，可令x=1.在二项式的展开式中，要注意项的系数和二项式系数的区别.

2.利用二项式定理求二项式中相关元素

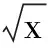
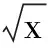
点评求二项式中某些项的二项式系数、常数项及其它一些待确定的问题是二项式定理最基本的应用.

3.利用二项式定理求展开式各项系数和(差)

A.1 B.-1 C.0 D.2

4.利用二项式定理求展开式中某项的系数

例4 在(x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5的展开式中，x2的系数等于____.

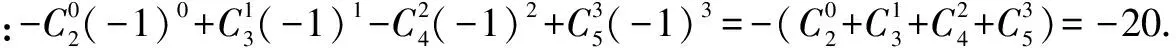
点评对于和式求特定项的系数问题，一般是分别求出再合并给出结论.

5.利用二项式定理确定展开式的最大(小)项

例5 在(x-1)9按x降幂排列的展开式中，系数最大的项是( ).

A.第4项和第5项 B.第5项

C.第5项和第6项 D.第6项

解根据二项式系数的性质，(x-1)9的展开展中的中间两项即第5项和第6项的二项式系数相等，同时取得最大值.但考察项的系数时，第6项系数需乘以(-1)得负，而第5项的系数为正，因此只有第5项的系数最大，而第6项的系数最小，选B.

6.利用二项式定理证明不等式

(*)

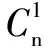
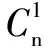
点评利用二项式定理的展开式，可以证明一些与自然数有关的不等式问题.题(1)中的换元法称为均值换元(或对称换元).这样消去δ的奇数次项，从而使每一项均大于或等于零.题(2)中，由对称位置二项式系数相等，把展开式倒过来写，再与原来的展开式相加，这样充分利用对称性来解题的方法是解决二项式展开式的常用方法.

7.利用二项式定理进行近似计算

例7 根据下列要求的精确度，求1.025的近似值.

①精确到0.01;

②精确到0.001.