纤维素热解动力学分析方法研究
2017-09-03周卫红丁毅飞徐安壮王玉杰丁伟婧
白 斌, 周卫红*, 丁毅飞, 徐安壮, 王玉杰, 丁伟婧
(1. 辽宁科技大学 土木工程学院, 辽宁 鞍山 114051; 2. 鞍钢集团工程技术有限公司, 辽宁 鞍山 114021)
·研究报告——生物质能源·
纤维素热解动力学分析方法研究
白 斌1, 周卫红1*, 丁毅飞2, 徐安壮1, 王玉杰1, 丁伟婧1
(1. 辽宁科技大学 土木工程学院, 辽宁 鞍山 114051; 2. 鞍钢集团工程技术有限公司, 辽宁 鞍山 114021)
以微晶纤维素为原料,在氮气气氛中利用热重分析仪考察了不同升温速率条件下纤维素的热解实验,分析了纤维素的热解动力学特性。采用双等双步法和Popescu法从热分析动力学的41种机理函数中选取最概然反应机理函数,同时运用Freeman-Carroll法、Coats-Redfern法、Starink法和双等双步法4种热分析方法计算热解反应活化能(E)、指前因子(A),并对结果进行了分析比较。结果表明,随着升温速率提高,纤维素热解起始温度增加,热失重速率升高;纤维素的热解过程可分为4个阶段:脱水预热(40~120 ℃)、热解初期(120~260 ℃)、主要热解失重(260~400 ℃)和炭化(400~900 ℃)。纤维素主要热解段分两个阶段进行,其活化能在低温段(260~350 ℃)时,为166~176 kJ/mol,高温段(350~400 ℃)时,为171~216 kJ/mol;采用反Jander动力学模型能较好地描述主要热解反应过程;采用单一扫描速率法(Freeman-Carroll法和Coats-Redfern法)分析结果与实际值有较大偏差,多重扫描速率法(Starink法和双等双步法)得到的结果更具可靠性。
纤维素;热解;热重分析;动力学
面对日益严重的能源短缺和环境污染问题,生物质作为一种清洁可再生资源受到人们越来越多重视。研究者通常采用热重分析方法对生物质进行热解动力学分析,揭示生物质的热解过程特性及热解规律。然而,在热分析动力学研究中,采用不同动力学分析方法以及不同最概然反应机理函数,求得的动力学参数差别较大[1]。目前,大多数研究者采用(一级或多级)反应级数机理函数对生物质进行热解动力学分析。王树荣等[2]采用微分法,假设反应为一级反应求解纤维素热解活化能,在低温段(570~610 K)具有高活化能,而高温段(610~640 K)具有低活化能。廖艳芬等[3]采用微商法求得纤维素的活化能,低温段(<600 K)活化能约为267 kJ/mol,高温段(>600 K)为174 kJ/mol左右。王文钊[4]采用Kissinger法、Coats-Redfern法[5]、Freeman-Carroll法[6]、Model-Free法及Malek法等5种动力学分析方法对纤维素进行分析发现,反应机理函数为一级反应,纤维素的热解活化能约为152.1 kJ/mol。黄娜等[7]采用Coats-Redfern法,发现纤维素低温热解为一级反应,活化能为185.58 kJ/mol,高温热解为二级反应,活化能为64.16 kJ/mol。然而,随着热分析方法的发展,研究者发现单一扫描速率法存在计算不精确等问题,国际热分析界呼吁应采用多重扫描速率法来研究固相反应本质[8]。然而,现有研究中将多重扫描速率法用于纤维素热解动力学分析的研究较少。谢华清等[9]采用Coats-Redfern法和等转化速率法中的Starink法[10]对生物质热解进行了比较分析,发现Starink法计算简单且结果合理。张保生等[11]利用Popescu法[12]研究了煤燃烧的动力学机理函数,认为所得结果具有较强的可信性。Zhang等[13]结合等转化率法和变异转化率法提出了一种新的热分析动力学方法——双等双步法。本研究尝试采用Popescu法和双等双步法确定机理函数,并用等转化速率Starink法和双等双步法进行纤维素的热动力学分析,同时与传统动力学分析方法(Freeman-Carroll法和Coats-Redfern法)进行比较,旨在分析各种热动力学分析方法的优缺点,寻找适合生物质热解的热动力学分析方法。
1 实 验
1.1 材料
高纯度微晶纤维素,购自Sigma公司,其粒度为20~100 μm,水分为6 %,密度为0.600 g/cm3。
1.2 仪器及方法
实验仪器采用德国耐驰公司TG209F3型热重分析仪(天平分辨度0.1 μg)进行纤维素热解。样品添加量为10 mg,坩埚采用Al2O3坩埚。热解实验在高纯氮气气氛下进行,流量为50 mL/min,初始温度为40 ℃,选择3种升温速率(10、20和30 K/min),热解终温为900 ℃。
1.3 热解动力学分析
热解过程动力学方程具体描述如下,固体分解反应动力学方程一般表示形式见式(1):
(1)

(2)
式中:f(α)—反应机理函数;α—转化率,α=(m0-mt)/(m0-m∞),m0,mt,m∞分别指样品的起始质量,某个时刻质量及反应结束达到稳定时的质量;t—反应时间,s;A—指前因子,min-1;E—活化能,kJ/mol;R—理想气体常数,8.314 J/(mol·K)。
(3)

(4)
对式(4)按不同方法积分或微分,则可求得动力学参数。
本实验首先采用Popescu法和双等双步法对文献[1]中41种反应机理函数进行筛选,结合模拟结果确定适合的反应机理函数。然后采用Freeman-Carroll法、Coats-Redfern法、Starink法和双等双步法4种热分析方法进行纤维素热解动力学分析,求解活化能(E)和指前因子(A),并比较4种方法的差异。
2 结果与讨论
2.1 热解特性分析
从图1看出,纤维素的热解过程可分为4个阶段:第1阶段为脱水预热阶段(40~120 ℃),主要是纤维素脱水过程;第2阶段为热解初期段(120~260 ℃),该温度段下,纤维素质量几乎没有发生变化,主要进行解聚及“玻璃化”转变[14];第3阶段为主要热解失重段(260~400 ℃),在该温度范围内纤维素的失重率约为80 %,纤维素大量发生裂解,分解为小分子物质,并伴随着挥发分的析出。第4阶段为炭化阶段(400~900 ℃),纤维素失重较为缓慢,主要发生聚合和炭化反应,最终生成焦炭和气体。
从图2可以看出,升温速率对热解区间及失重速率影响较大,对热解总质量损失影响较小。随着升温速率的提高,纤维素热解起始温度有所提高,由260 ℃提高到280 ℃,最大热解失重速率峰对应温度升高,由350 ℃增加到369.6 ℃,主要热解区间也向高温移动。这是因为升温速率越高,样品热解达到终温所用时间越短,反应程度越低,同时会影响样品内外温差和温度梯度,导致热滞后现象加重,因此热解温度向高温侧移动[15]。最大热解失重速率也有所增加,由18.69 %/min增加到48.79 %/min,从传热角度分析,这主要是由于升温速率较快,使达到热解温度所需时间变短,热解速率随之加快。
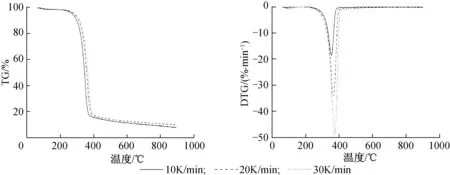
图2 不同升温速率下纤维素的DTG曲线
Fig. 2 DTG curves of cellulose at different heating rates
2.2 热解机理函数
2.2.1 热解机理函数的筛选 本实验采用两步反应模型描述纤维素热解机理,对纤维素主要热解反应低温段(260~350 ℃)与高温段(350~400 ℃)运用Popescu法与双等双步法对文献[1]中41种机理函数进行分析计算,选取不同反应区间适合的反应机理函数,经过计算发现两段温度区间所对应的适合反应机理如表1和表2所示。
由表1和表2可知,高温段、低温段对应着多种机理函数,需要对所选机理函数使用1Stopt软件(七维高科公司开发的数值优化分析计算软件)进行DTG曲线模拟,并与实验DTG曲线对比以达到对机理函数进一步筛选,最终选取适合的反应机理函数。

表1 低温段(260~350 ℃)机理函数

表2 高温段(350~400 ℃)机理函数
2.2.2 最佳机理函数的确定

(5)
从式(5)通过代入不同的反应机理函数,可以得出不同机理函数下的转化率α表达式。
生物质热失重速率可表示为:
(6)
利用式(5)和(6)可以得出不同机理函数下热失重速率表达式,采用1Stopt软件进行非线性最小平方拟合优化动力学参数,目标函数如下:
(7)
2.2.2.2 模拟结果 采用升温速率β=10 K/min的纤维素热解DTG数据对适合的机理函数进行比较分析,其结果见图3和图4,计算结果见表3。
比较图3、图4拟合情况可知,8号机理函数的高、低温段拟合程度最好,R2都在0.99以上(见表3),同时本研究还特意在高温段分析了16号机理函数,发现以往常用的16号一级反应机理函数对纤维素的低温热解有很高的拟合度,而对高温段的热解描述很差,不宜用来对纤维素热解进行分析;比较各温度段下计算所得的活化能与指前因子数值,发现采用不同的机理函数,最终计算出的热解活化能与指前因子差别极大,引入反应机理函数求解活化能的方法值得慎重考虑。因此,本研究尝试采用8号反Jander方程(机理为三维扩散)作为纤维素低温、高温段的最佳反应机理函数建立两步反应模型,讨论不同动力学分析方法的差异。

图3 低温段机理函数比较Fig. 3 Comparison of mechanism functions of low temperature section

图4 高温段机理函数比较Fig. 4 Comparison of mechanism functions of high temperature section

函数号No.低温段(260~350℃)lowtemperaturesectionR2A/min-1E/(kJ·mol-1)函数号No.高温段(350~400℃)hightemperaturesectionR2A/min-1E/(kJ·mol-1)80.994141.19×1012154.0650.977013.12×10-7 50.37160.9915691456356.2280.990376.12×1020203.98190.983495.43×10-7186.92160.76429——280.99048221134.74220.977046.982×10-975.43290.990891508842.06230.977041.572×10-9100.57
2.3 热解动力学分析
2.3.1 热解动力学分析方法

(8)
将一组实验数据[Ti,αi(i=1,2,…,m)]代入式(8),将式左端项对式右端大括号项作图,根据斜率即可求得活化能E,截距求得反应级数n。
2.3.1.2 Coats-Redfern法 Coats-Redfern是将式(4)右端积分项取一级近似并对两边取对数,得式(9):
(9)
式(9)线性回归为一条直线,根据其斜率求取E,截距即可求得指前因子A。
2.3.1.3 Starink法 Starink法是通过对KAS法和FWO法讨论总结提出的一种精确度更高的分析法,其特点是动力学计算不涉及反应机理函数f(α),具体形式见式(10):
(10)
固定某一转化率,在多组升温速率下线性拟合得到一组直线,通过斜率、截距分别求出不同转化率下的活化能E、指前因子A。
2.3.1.4 双等双步法 此方法将Flynn-Wall-Ozawa法[16]方程改写,具体形式见式(11):
(11)
2.3.2 热解动力学参数的求解 动力学参数的求解结果见表4~表6。

表4 Freeman-Carroll法计算的动力学参数

表5 Coats-Redfern法计算的动力学参数

表6 Starink法和双等双步法计算的动力学参数
从4种不同的动力学分析方法结果可以看出,通过不同方法计算的纤维素热解活化能差别较大。对比发现,Freeman-Carroll法采用单步反应模型对纤维素热解主要温度区间进行拟合的线性很差,活化能在83~105 kJ/mol范围内(见表4)。Coats-Redfern法采用两步反应模型,拟合结果表明纤维素热解在主要失重阶段呈现两段分布,低温段表现出较好线性关系,而高温段的线性较差;在低温段,纤维素的活化能随着升温速率的提高而降低,在143~155 kJ/mol之间变化,而高温段活化能随着升温速率的提高而升高,由13 kJ/mol升高至46 kJ/mol(见表5)。
根据公式α=(m0-mt)/(m0-m∞),结合TG实验数据,可以得到转化率与温度的对应关系曲线(见图5)。从图5可知,随着热解温度的增加,纤维素转化率逐渐增加。采用双等双步法和Starink法对纤维素热解进行线性拟合,其表现出了极好的线性(见图6和图7),除在转化率90 %处相关性为0.95左右,其余相关性都在0.99以上,活化能随着转化率的增加略有增加(见表6)。采用Starink法和双等双步法求解动力学参数,发现在低温段(转化率为10 %~70 %对应温度区间为300~350 ℃)活化能变化幅度不大,保持在166~176 kJ/mol之间,指前因子除转化率为10 %外,其余基本保持在相同数量级内变化。高温段(转化率为70 %~90 %对应温度区间为350~400 ℃)时出现明显差别,活化能从相对稳定值171 kJ/mol急增到216 kJ/mol,同样地,指前因子也提高了2~3个数量级,增幅较大。这表明纤维素主要热解分2个阶段进行,证实实验采用两步反应模型合理可行。

图5 转化率曲线
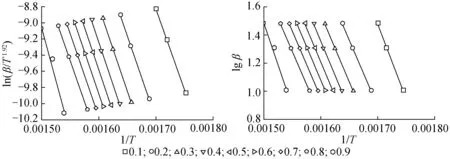
图6 Starink法拟合曲线 图7 双等双步法拟合曲线
Fig. 6 Fitting curves by Starink method Fig. 7 Fitting curves by doubel equal-doubel steps method
2.3.3 模拟结果验证与分析 利用1Stopt软件根据纤维素在10、20和30 K/min升温速率下的热解DTG曲线分别对其高温、低温段数据建立两步反应模型,采用的机理函数均为反Jander方程,通过拟合结果与实验值比较,验证所采用的机理函数及4种动力学分析方法所得结果的正确性。模型拟合曲线见图8,动力学参数计算结果见表7。
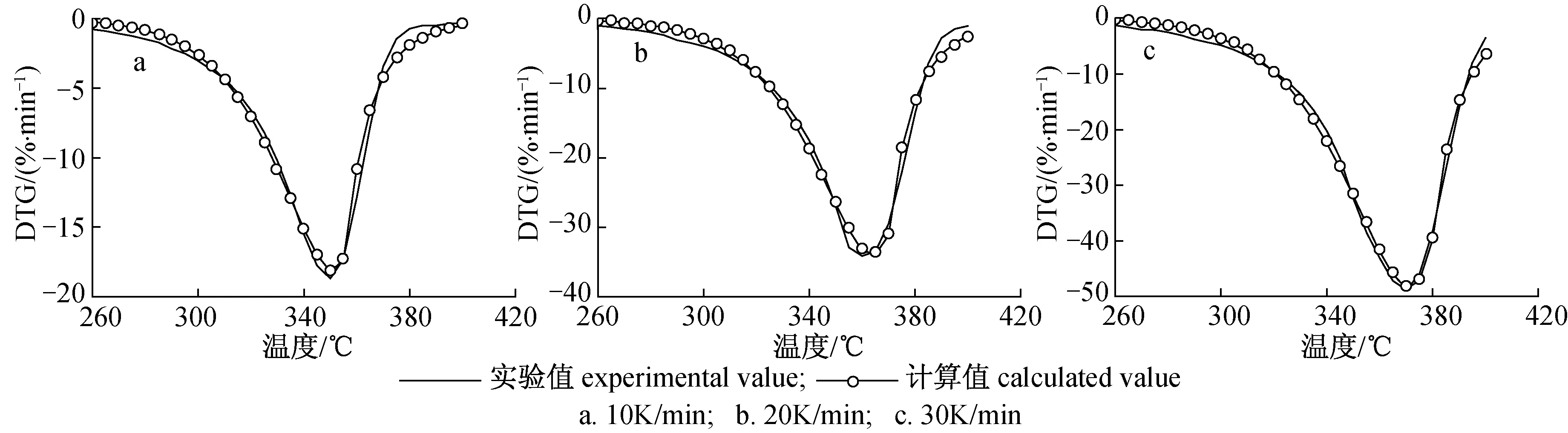
图8 模型模拟曲线

升温速率/(K·min-1)heatingrate低温段(260~350℃)lowtemperaturesection高温段(350~400℃)hightemperaturesectionE/(kJ·mol-1)A/min-1R2E/(kJ·mol-1)A/min-1R210154.0581.19×10120.99414203.9786.12×10200.9907320152.5219.29×10110.99265210.6121.11×10200.9842330145.2122.57×10110.99465220.8632.54×10200.96983
结合模拟曲线图8与参数计算值表7,对照4种动力学分析方法计算结果,发现在低温段模型模拟所得动力学参数结果与Coast-Redfern法极为接近,高温段与多重扫描速率法(Starink法和双等双步法)极为接近,说明尝试采用反Jander动力学机理函数较好地描述了纤维素主要热解过程。
建立模型进行热解模拟优势在于能够进行成百上千次的迭代优化,使得计算结果更加接近真实值,这样很好地弥补了Coast-Redfern法在高温段拟合线性差的问题,但是低温段模型的模拟值与多重扫描速率法的计算值还是有一定的差距,可能的原因是: 1) 反应机理函数的引入,无论采用Freeman-Carroll法、Coast-Redfern法还是模型模拟都固化了纤维素热解过程,认为其是一成不变的简单热解过程,不管采用单步反应模型(Freeman-Carroll法)还是两步反应模型(Coast-Redfern法),目的都是为了尽可能地逼近真实反应过程,然而再好的机理函数与真实反应过程都是存在差距的,这必然使得计算结果与真实值存在偏差; 2) 多重扫描速率法尽管很好地避免了机理函数的引入,然而该方法是根据多条TG曲线进行的动力学分析,可能使得所求结果是真实值的平均值,更多地代表真实值的范围。
2.4 热解动力学分析方法比较
通过分析方法对比表明,分析方法、升温速率、拟合区间等因素对热分析结果均有影响。尽管不同热分析方法求解结果都能反映出纤维素热解特性,但具体计算方法不同,其结果相差很大。
在单一扫描速率方法中,Freeman-Carroll法的线性拟合最差;而Coats-Redfern法在低温段能够进行线性拟合且拟合较好,在高温段虽然能够进行线性拟合,但拟合情况并不理想。出现以上结果的原因主要有: 1) 选取机理函数的正确性。Freeman-Carroll法机理函数采用反应级数方程f(α)=(1-α)n,而前文分析认为最佳机理函数是反Jander方程,由于机理函数的差异,导致结果差距很大,Sestak等学者认为像Freeman-Carroll法等建立在单一动力学机理函数上的方法应慎用甚至不用,除非真实的机理函数确实如此[17-18]。2) 反应模型的合理性。Freeman-Carroll法采用单步反应模型,Coats-Redfern法采用两步反应模型,从两者的拟合曲线来看,两步反应模型更适合描述纤维素的主要热解过程。笔者在后续工作中也采用Freeman-Carroll法建立两步反应模型进行了分析(文中未列出),发现Freeman-Carroll法对低温段拟合较好但计算值偏差太大,高温段拟合极差。3) 机理函数与真实机理存在差距。纤维素热解过程复杂多变,本研究采用的2种单一扫描速率法在主要热解区间内始终用简单的反应机理函数来描述整个热解失重过程并不科学[19],即使2.2节中分析认为反Jander方程为最佳机理函数,且均适用于高温段和低温段,但是高温段仍然存在线性拟合效果差的问题。
对比单一扫描速率法与多重扫描速率法,发现单一扫描速率法所得活化能相对较低,这说明由于引入机理函数的缘故,单一扫描速率法计算值可能会较多地偏离实际值[20],而多重扫描速率法则避免了因反应机理函数的假设差异而带来的误差[21],使得计算结果可靠性更高;同时发现,热解过程由低温向高温过渡时,2种方法所得活化能都存在较大变化,说明纤维素的热解过程是分2个阶段进行的,正如Broido-Shafizadeh模型[22]所描述的纤维素热解过程,纤维素在热解过程中存在2个竞争反应,低温段有利于焦炭的生成而高温段偏向于生成挥发分。
3 结 论
3.1 以微晶纤维素为原料,利用热重分析仪探讨了纤维素的热解动力学特性。结果表明,纤维素的热解过程可分为4个阶段:脱水预热(40~120 ℃)、热解初期(120~260 ℃)、主要热解失重(260~400 ℃)和炭化(400~900 ℃)。随着升温速率的增大,纤维素热解过程向高温方向移动,纤维素最大热解速率增加,对应热解温度升高,但在不同的升温速率下最终残余量基本一致。

3.3 运用4种动力学分析方法对纤维素的热解进行线性回归拟合求解其活化能。结果发现,纤维素热解分两步进行,其活化能在低温段(260~350 ℃)时为166~176 kJ/mol,高温段(350~400 ℃)时为171~216 kJ/mol。比较各方法所得拟合曲线,发现单一扫描速率法(Freeman-Carroll法和Coats-Redfern法)线性拟合较差,而多重扫描速率法(Starink法和双等双步法)线性拟合很好。说明Starink法和双等双步法所得到的热解活化能较为准确可信,分析认为单一扫描速率法始终采用单一反应机理函数导致分析结果偏差较大,而多重扫描速率法避免了引入反应机理函数的影响,使得分析结果更加可靠。
[1]胡荣祖,史启祯. 热分析动力学[M]. 北京:科学出版社,2008.
[2]王树荣,廖艳芬,骆仲泱,等. 氯化钾催化纤维素热解动力学研究[J]. 太阳能学报,2005,26(4):452-457.
[3]廖艳芬,王树荣,骆仲泱,等. 纤维素热裂解过程动力学的试验分析研究[J]. 浙江大学学报:工学版,2002,36(2):172-176.
[4]王文钊. 纤维素热重分析及热解动力学研究[D]. 重庆:重庆大学硕士学位论文,2008.
[5]COATS A W,REDFERN J P. Kinetic parameters from thermgravimetric data[J]. Nature,1964,201(1):68-69.
[6]FREEMAN E S,CARROLL B. The application of the thermoanalytical techniques to reaction kinetics: The thermogravimetric evaluation of the kinetics of the decomposition of calcium oxalate monohydrate[J]. The Journal of Physical Chemistry,1958,62(4):394-397.
[7]黄娜,高岱巍,李建伟,等. 生物质三组分热解反应及动力学的比较[J]. 北京化工大学学报,2007,34(5):461-465.
[8]张彩霞,任宁,张洁,等. 双等双步法对二水合草酸镁的脱水过程的动力学研究[J]. 河北北方学院学报,2009,25(5):23-26.
[9]谢华清,于庆波,秦勤,等. 生物质热解过程两种动力学分析方法的比较[J]. 东北大学学报,2013,34(6):845-848.
[10]STARING M. The determination of activation energy from linear heating rate experiments:A comparison of accuracy of isoconversion methods[J]. Thermochimica Acta,2003,404(1/2):163-176.
[11]张保生,刘建忠,周俊虎,等. 利用Popescu法对煤燃烧反应机理的研究[J]. 中国电机工程学报,2006,26(15):68-72.
[12]POPESCU C. Integral method to analyze the kinetics of heterogeneous reactions under non-isothermal conditions a variant on the Ozawa-Flynn-Wall method[J]. Thermochimica Acta,1996,285(2):309-323.
[13]ZHANG J J,REN N. A new kinetic method of processing TA data[J]. Chinese Journal of Chemisrty,2004,22(12):1459-1462.
[14]ANTAL M J,VARHEGYI G. Cellulose pyrolysis kinetics: The current states of knowledge[J]. Industrial & Engineering Chemistry Research,1995,34(3):703-717.
[15]王树荣. 生物质热裂解制油的试验与机理研究[D]. 杭州:浙江大学博士学位论文,1999.
[16]FLYNN J H,WALL L A. General treatment of the thermogravimetry of polymers[J]. Journal of Research of the National Bureau of Standards—A. Physics and Chemistry,1996,70A(6):487-523.
[17]KOGA N,MALEK J,SESTAK J,et al. Data treatment in non-isothermal kinetics and diagnostic limits of phenomenological models[J]. Netsu Sokutei,1993,20:210-223.
[18]SESTAK J,MALEK J. Diagnostic limits of phenomenological models of heterogeneous reactions and thermal analysis kinetics[J]. Solid State Ionics,1993,65(9):245-254.
[19]何宏舟,骆仲泱,岑可法. 不同热分析方法求解无烟煤燃烧反应动力学参数的研究[J]. 动力工程,2005,25(4):493-499.
[20]宋春财,胡浩权,朱盛维,等. 生物质秸秆热重分析及几种动力学模型结果比较[J]. 燃料化学学报,2003,31(4):311-315.
[21]曾凡阳,刘朝,王文钊,等. 生物质热重实验及动力学分析[J]. 工业加热,2008,37(3):6-8.
[22]BRADBURY A G W,SAKAI Y,SHAFIZADEH F. A kinetic model for pyrolysis of cellulose[J]. Journal of Applied Polymer Science,1979, 23(11):3271-3280.
Analysis Method of Cellulose Pyrolysis Dynamics
BAI Bin1, ZHOU Weihong1, DING Yifei2, XU Anzhuang1, WANG Yujie1, DING Weijing1
(1. School of Civi Engineering,University of Science and Technology Liaoning, Anshan 114051, China; 2. Ansteel Engineering Technology Co.,Ltd., Anshan 114021, China)
With microcrystalline cellulose as raw material, cellulose pyrolysis experiments under different heating rates were carried out in nitrogen atmosphere by thermogravimetric analyzer, and the pyrolysis kinetic characteristics of cellulose were analyzed. The most probable reaction mechanism function was selected from 41 mechanism functions of thermal analysis kinetics by using the double equal-double steps method and Popescu method, meanwhile, four different thermal analysis methods (Freeman-Carroll method, Coats-Redfern method, Starink method, double equal-double steps method) were used to calculate the activation energy (E) and pre exponential factor (A) of pyrolysis reaction, and the results were analyzed and compared. The results showed that with the increase of the heating rate, the initial pyrolysis temperature of cellulose increased and the rate of pyrolysis weight loss increased; the pyrolysis process of cellulose could be divided into 4 stages, dehydration preheating section (40-120 ℃), the early period of pyrolysis (120-260 ℃), the main pyrolysis section (260-400 ℃) and carbonization section (400-900 ℃); the main cellulose pyrolysis section was divided into two stages and the activation energies at low temperature (260-350 ℃) and high temperature (350-400 ℃) were 166-176 kJ/mol and 171-216 kJ/mol, respectively; anti Jander kinetic model could describe the reaction process of main pyrolysis well; by using single scanning rate method (Freeman-Carroll and Coats-Redfern), the analysis result had a great deviation from the actual value, and the results obtained by the multiple scan rate method were more reliable.
cellulose;pyrolysis;thermogravimetric analysis;dynamics
10.3969/j.issn.1673-5854.2017.04.002
2016-10-16
辽宁省教育厅一般项目(L2014121);辽宁科技大学研究生教育改革与科技创新创业项目(LKDYC201614)
白 斌(1992— ),男,山西阳泉人,硕士生,主要从事生物质热解催化气化研究
*通讯作者:周卫红,副教授,硕士生导师,主要从事生物质能源综合利用等方面研究;E-mail:zwh_0190@sina.com。
TQ35
A
1673-5854(2017)04-0008-09
