不同地基模型对拱坝动力响应的影响
2017-09-03李树山刘祖军贾明晓
李树山,刘祖军,贾明晓,解 伟
(华北水利水电大学,河南郑州450045)
不同地基模型对拱坝动力响应的影响
李树山,刘祖军,贾明晓,解 伟
(华北水利水电大学,河南郑州450045)
在粘弹性人工边界理论基础上,结合波场分解法的地震动输入方法,应用ANSYS软件的参数化语言APDL,编制了模拟粘弹性人工边界和地震荷载输入的程序。针对某碾压混凝土拱坝建立了“库水-拱坝-地基”联合作用的有限元模型,采用施加粘弹性边界并输入相应地震动,讨论了无限地基辐射阻尼的影响,并与无质量地基模型的计算结果进行比较分析。研究结果表明,只有考虑辐射阻尼效应才会得到符合实际情况的坝体地震响应结果,因此实际工程抗震分析时对地基的模拟应该合理选取。
拱坝;动力响应;粘弹性人工边界;无质量地基
0 引 言
在超高大坝、超长桥梁、超高建筑等大型结构动力响应分析中,其刚度、重量、跨度都很大而地基往往相对较柔,刚性地基假定不符合实际情况,需要考虑无限地基能量辐射效应的影响。另外,结构体系的动力响应分析属于开放系统中的近场波动问题,也需要考虑“地基-结构”动力相互作用的影响。而“地基-结构”的相互作用机理复杂,计算量大,难以获得试验检验。由于难以获得实际场地资料,不同的计算模型得出的计算结果差别很大。这也是高拱坝抗震响应分析中亟待解决的基本问题。目前,采用有限元法模拟“结构-地基”的相互作用,一般需要引入人工边界。广义上,人工边界可分为精确边界和局部边界。其中,局部边界在时间和空间上是局部解耦的,计算机存储量小,计算时间短,实用性较强,因而得到广泛研究和应用。
地震作用下的“拱坝-地基”系统是一个能量开放系统,坝体与地基之间存在不可忽视的能量交换。对于能量开放系统的地震响应模拟,关键问题是如何采用人工边界模拟方法将无限模型转换为便于在计算机上实现的有限模型。文献[1-2]介绍了常见人工边界处理方法。杜修力等[3]将无限域的远场波动位移解假定为无衰减的平面波位移解与无限域格林函数解的远场近似位移解的组合,建立了一种新的粘弹性人工边界条件,使人工边界结合显式有限元的完全解耦的近场波动数值模拟方法具有了统一的稳定性评判标准,该方法对边界的模拟精度高于二阶透射边界[4]。
近年来,国内外学者提出了多种人工边界模拟方法。其中,粘弹性边界条件原理简单,精度比较高,仅需在边界添加弹簧和阻尼即可实现,便于和有限元软件进行结合。Lysmer和Kuhlemeyer提出粘弹性人工边界[5],该方法相当于在边界上施加一段固定的单向粘滞阻尼器,只能考虑边界阻尼的吸能作用,在应用中容易发生结构整体漂移,精度不高。Deeks和Randolph给出了二维平面应变问题的粘弹性边界表达式[6],开始了真正的时域解耦的粘弹性边界研究。刘晶波等[7]将平面应变膨胀波边界应用于二维平面问题的分析,并给出了粘弹性边界反射系数和一种有效外源输入方法,即把输入地震动转化为作用于人工边界上的等效荷载的方法来实现波动输入。杜修力[8]提出了基于考虑散射波远场几何衰减的平面波建立粘弹性人工边界的方法,并与显式有限元法结合,建立局部解耦的时域波分析方法。王振宇[9]利用极坐标球面波近似表达方法,建立了一种三维粘弹性人工边界。
本文在现有研究成果基础上,利用ANSYS软件建立了“拱坝-地基”系统的粘弹性地基模型,通过波场分解方法实现粘弹性地基模型的地震波等效荷载的输入,对比分析了“拱坝-地基”系统采用无质量地基模型和粘弹性地基模型2种情况下拱冠关键点处的动力响应,分析了引起2种模型计算结果差别较大的原因,其研究成果能够为拱坝抗震的精细化分析提供参考。
1 三维粘弹性人工边界模型
1.1 三维粘弹性动力人工边界方程
根据近场弹性波理论,可以推导出三维粘弹性人工边界方程。
1.1.1 法向边界条件
球坐标系中球面膨胀波(P波)的波动方程
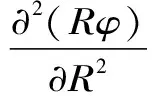
(1)
式中,φ为位移势函数;cp为介质的P波波速;R为径向坐标。方程式的通解可表示为
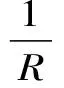
(2)
式中,f(*)和g(*)为任意函数,分别表示外行扩散波和内行会聚波。考虑外行扩散波,垂直于波阵面的位移可写为
u=
(3)
法向应力的计算公式为
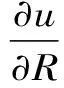
(4)
式中,λ和μ为拉梅常数。由此可得
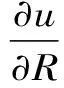
(5)
(6)
因此,可以得到波振面上用函数表示的法向应力为
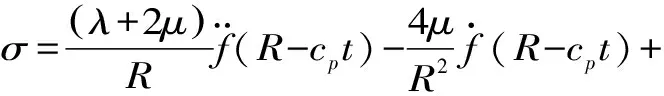
(7)
为建立法向应力σ和位移u之间的关系式,引入以下方程
(8)
(9)
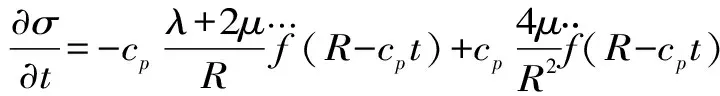
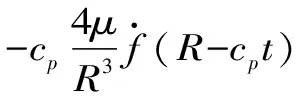
(10)
(11)
式(11)即为三维法向人工边界方程,方程给出了波阵面上法向应力与位移的关系,式中G=μ为介质剪切模量,ρ为介质密度。
建立三维人工边界需要将无限介质截断,在截断处,在人工边界上施加连续的弹簧-阻尼器集中质量系统。系统方程
(12)
(13)
式中,uR和um分别表示人工边界节点与集中质量沿荷载作用方向的位移。
由式(12)可得
(14)
再对式(14)求导可得
(15)
由此可得关于施加物理系统人工边界节点应力与位移满足的微分方程
(16)
将式(11)和式(16)进行比较分析,可以得到物理方程的参数为
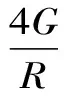
(17)
这时只需要采用相应参数的弹簧,阻尼器和集中质量单元即可实现三维粘弹性人工边界,可以保证人工边界上力和位移的条件和连续介质完全相同(如图1所示)。
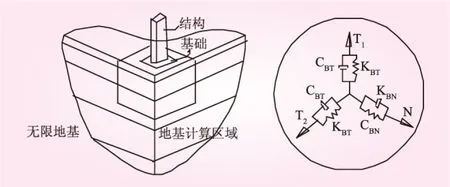
图1 人工边界等效弹簧-阻尼器系统
1.1.2 切向边界条件
球坐标系中球面剪切波(S波)的波动方程为
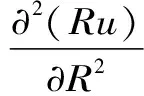
(18)
它的位移近似解为
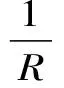
(19)
同理,可以得到施加在边界上物理方程参数为
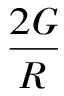
(20)
1.2 三维粘弹性静动力统一人工边界方程
目前,许多工程问题需要综合考虑静力效应及动力效应,解决的办法是采用静力人工边界和动力人工边界对静力问题和动力问题分别进行计算,考虑折减系数后进行叠加得到最后结果。如果考虑非线性问题,上述叠加原理不能应用于大型拱坝的强地震响应分析,因而有必要发展静动力统一人工边界来适应这种情况。一般情况下,动力人工边界和静力人工边界是分别基于动力学和静力学的基本理论建立的,因而试图从基本理论出发建立静动力统一人工边界存在着很大的难度。可行的方法是首先基于动力学基本理论,建立适用于动力问题分析的动力人工边界;然后对其进行修正,使之能够适用于静力问题的分析。理论上,动力人工边界的确定是一个低频问题,采用弹簧及阻尼器构建的动力人工边界,计算精度取决于其静力特性。根据这一原则,如果能够修正粘弹性动力人工边界,使之用于静力问题时具有足够高的精度,则其对动力问题的模拟精度也可能得到进一步提高。因此,需要对动力问题中的参数进行修正。即
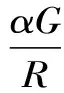
(21)
参数α根据人工边界的类型及设置方向取值
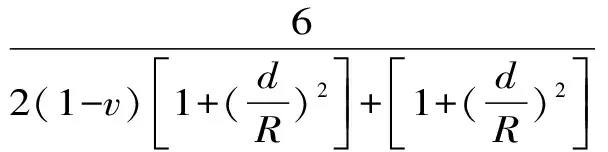
(22)
式中,v为泊松比;d为坐标位置;R为荷载作用点到人工边界点的距离。对于底面人工边界,d=r;对于侧面人工边界,d=z。对于集中荷载,R可取为加载点至人工边界的垂直距离;对于分布荷载,R可取为分布荷载中心至人工边界的垂直距离。
2 地震荷载的输入
地震波的波动源来自人工边界外的无穷远,地震波入射属于外源问题。为保证人工边界的精度,常采用2种输入波方法,即等效边界力法和波场分解法。
本文采用杜修力等[10]提出的波场分解方法进行计算。根据人工边界上的波场特点,不同边界面采用不同的分解方法:在底边界上将总场分解为边界入射场和边界外行场,侧边界上将总场分解为自由场和散射场。边界入射场或自由场可由连续介质力学模型解析计算得到,边界外行场或散射场由人工边界条件模拟并由离散模型依据数值分析方法获得。上述方法在尽量避免计算自由场的前提下较好地解决了人工侧边界面的平行波模拟问题。将未知的散射场或边界外行场用总场减去自由场或边界入射场(用上标R表示)表示,得到含外源作用的人工边界面l结点i方向的有限元运动方程为:
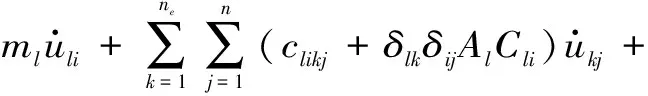
(23)
(24)
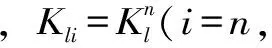
假定底边界竖直入射的P波位移时程为up(t)和S波的位移时程为us(t),按式(24)解析计算各人工边界结点的等效地震荷载fli(t),人工边界l结点的计算公式为
P波入射
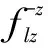
(25)
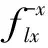
(26)
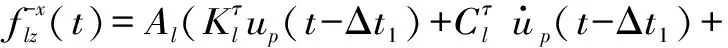
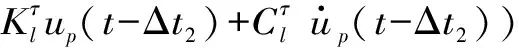
(27)
(28)
(29)
(30)
S波入射
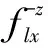
(31)
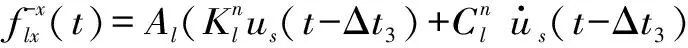
(32)
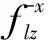
(33)
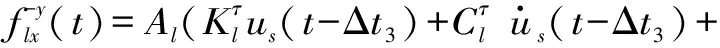
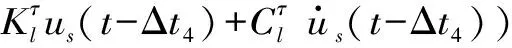
(34)
(35)
(36)
式中,Δt1=l/cp,Δt2=(2×L-l)/cp,Δt3=l/cs,Δt4=(2×L-l)/cs;ρ、cp、cs、λ分别为介质密度、P波波速、S波波速、第一拉梅常数;L为底边界到地表的距离;l为l结点到底边界的距离;Δt1和Δt2分别为l结点处入射P波和地表反射P波的时间延迟;Δt3和Δt4分别为l结点处入射S波和地表反射S波的时间延迟;等效地震荷载的下标代表结点号和分量方向,上标代表结点所在人工边界面的外法线方向,与坐标轴方向一致为正,相反为负。
3 算例分析
3.1 工程概况及计算模型的建立
某大型碾压混凝土拱坝,最大坝高132 m,坝顶总长250.25 m,坝顶厚9.5 m、宽28 m,厚高比0.238,为三心圆重力拱坝。该拱坝按50年一遇设计洪水标准,按500年一遇校核洪水标准,建筑物区地震基本设计烈度为Ⅷ度。
计算参数选择:坝体混凝土材料静弹性模量E=2.0×104MPa,泊松比系数0.167,容重2 400 kg/m3。在动力计算中不考虑地基的质量,混凝土动力弹性模量是静力计算的1.3倍。库水密度为1 000 kg/m3,可压缩性库水体积压缩模量E=2.0×103MPa。
计算模拟范围为:上游面水体和地基均为3倍坝高,左右岸及自坝底向下均为1.5倍坝高,下游面地基1.5倍坝高。库水采用ANSYS软件的fluid30单元进行模拟,并对库水上游面的无穷远处施加无穷远边界进行模拟。坐标原点在拱坝第一个圆心处,X为顺河向,下游为正方向,Z为横河向,向左岸为正方向,Y为竖直向,向上为正方向,全部边界取法向约束。拱坝坝体的有限元模型如图2所示。
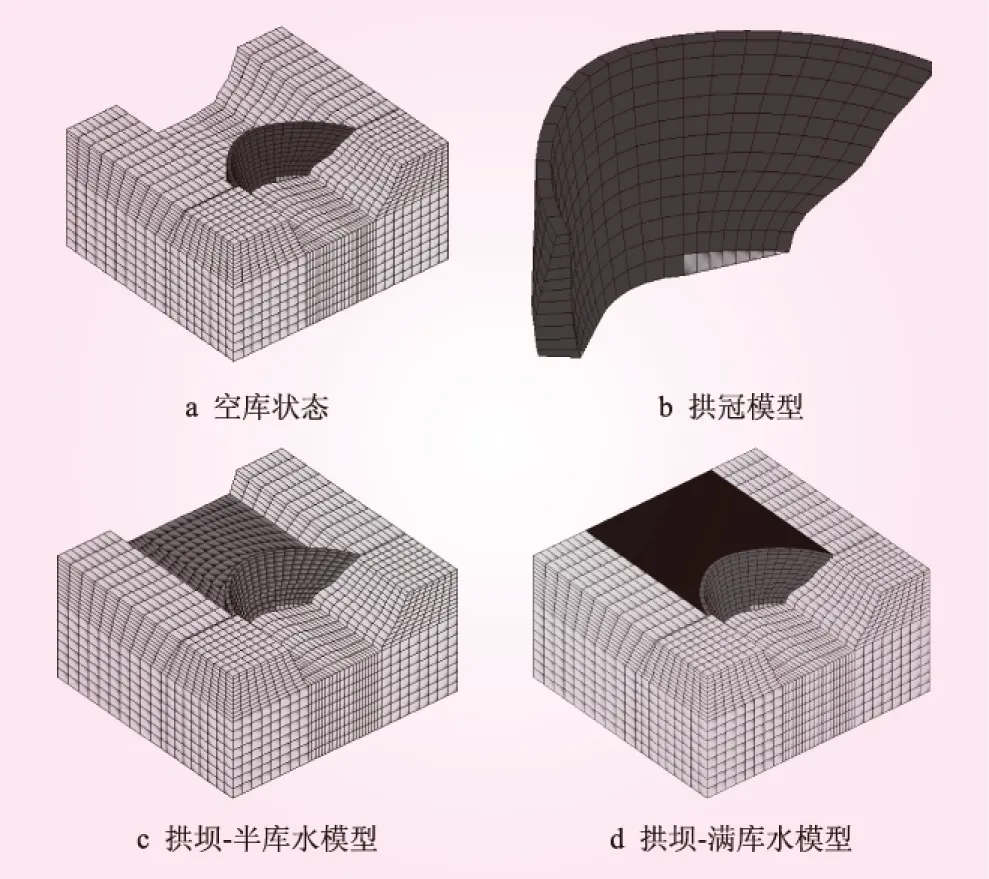
图2 拱坝有限元计算模型
3.2 动力时程响应分析
根据建立的“库水-拱坝-地基”有限元模型,分别计算了采用无质量地基模型和粘弹性地基模型,且处于不同库水水位时“库水-拱坝-地基”系统的动力响应。计算所采用的地震波为EI-Centro波,其加速时程曲线如图3所示。
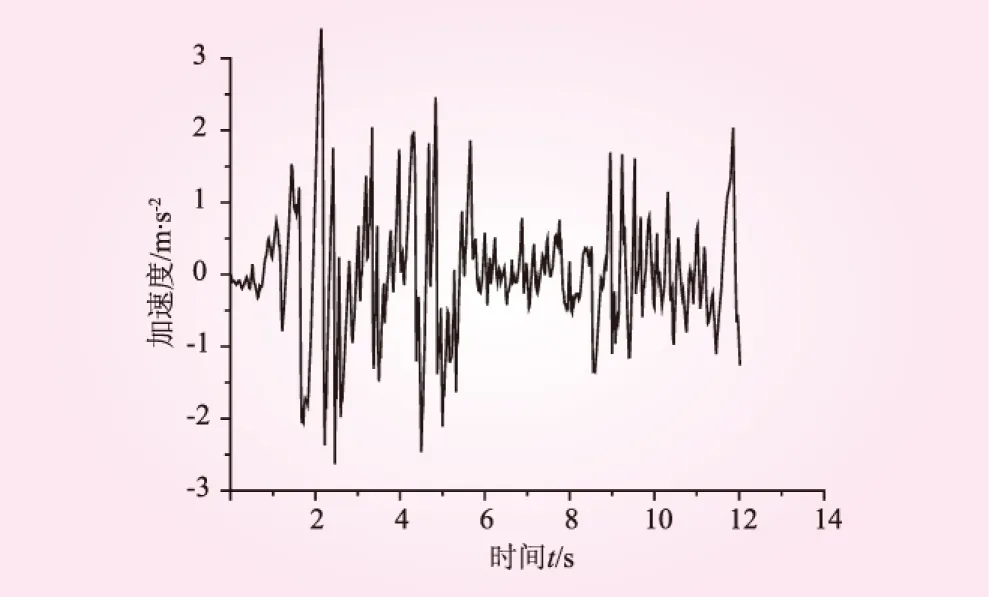
图3 EI-Centro波实测加速度时程
3.2.1 无质量地基模型计算结果分析
图4~图6给出了空库、半库水和满库水时采用无质量地基模型时拱坝坝顶拱冠处关键点位移和应力情况。空库状态时,采用无质量地基模型计算的坝顶最大位移11.16 mm,拱顶最大拉应力1.076 MPa,最大压应力1.14 MPa。半库水时,坝顶最大位移8.03 mm,拱顶最大拉应力0.77 MPa,最大压应力0.73 MPa。满库水时,坝顶最大位移10.6 mm,拱顶最大拉应力 1.42 MPa,最大压应力1.14 MPa。
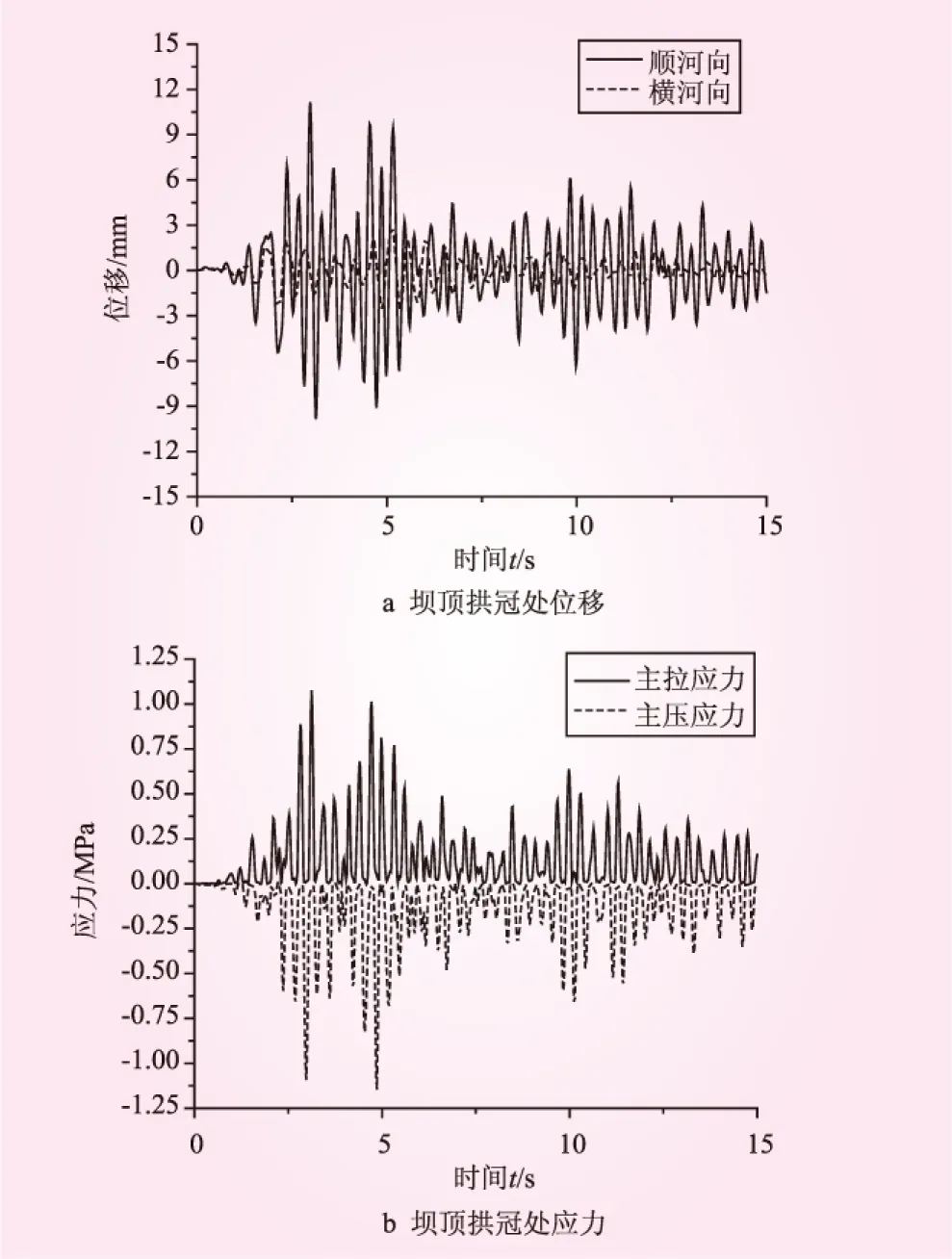
图4 空库状态下拱坝的位移和应力响应(无质量地基模型)
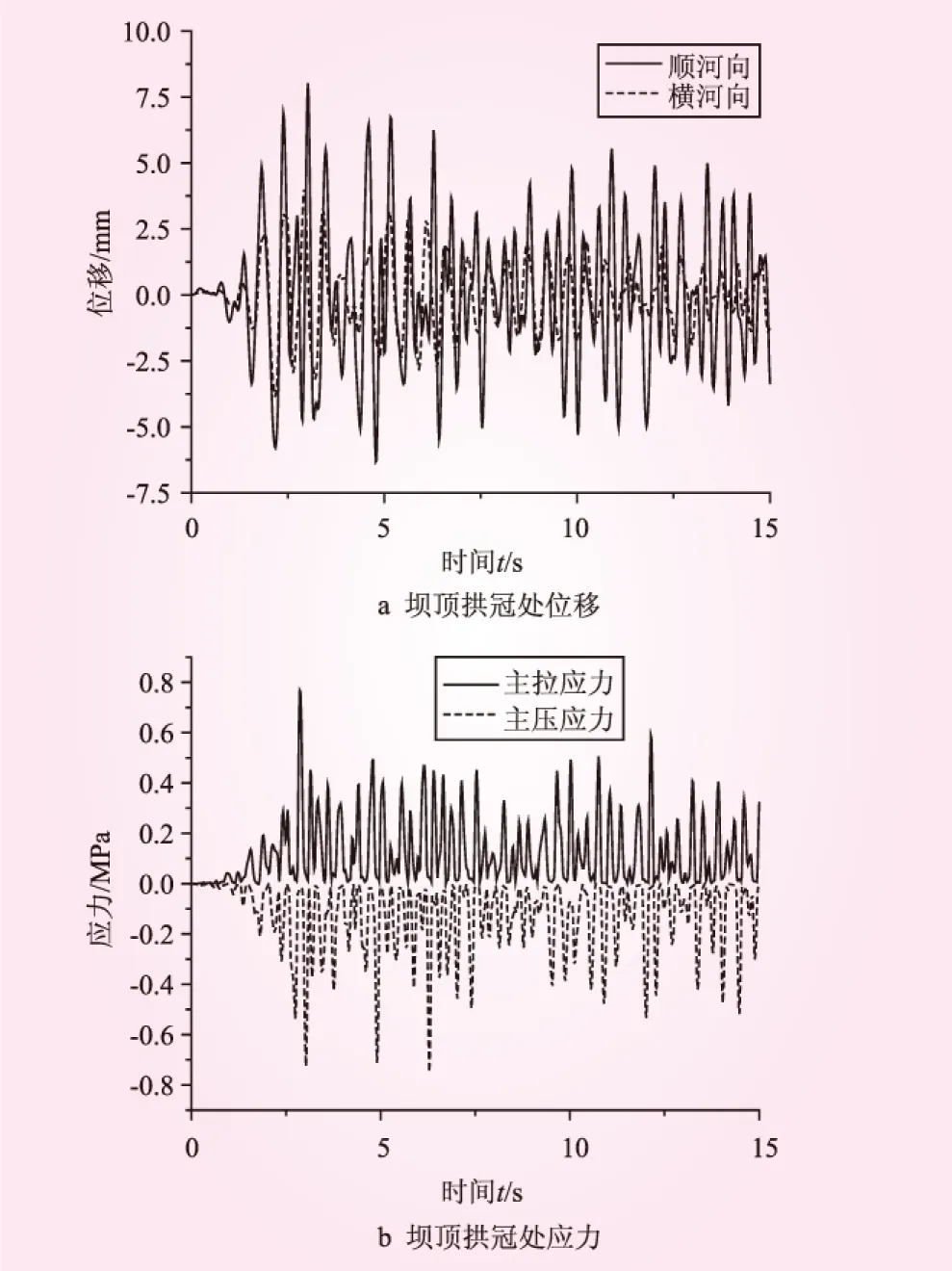
图5 半库水状态下拱坝的位移和应力响应(无质量地基模型)
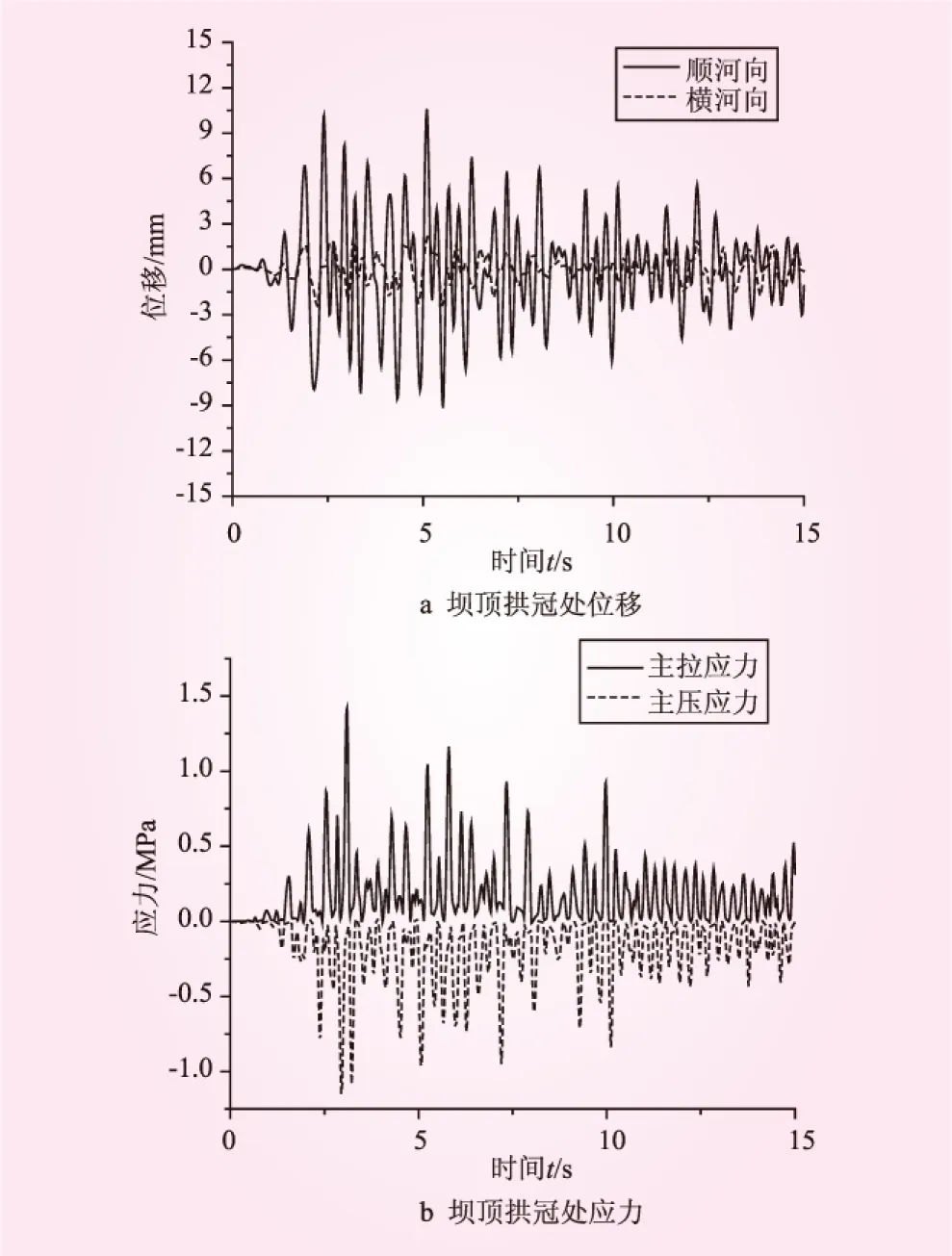
图6 满库水状态下拱坝的位移和应力响应(无质量地基模型)
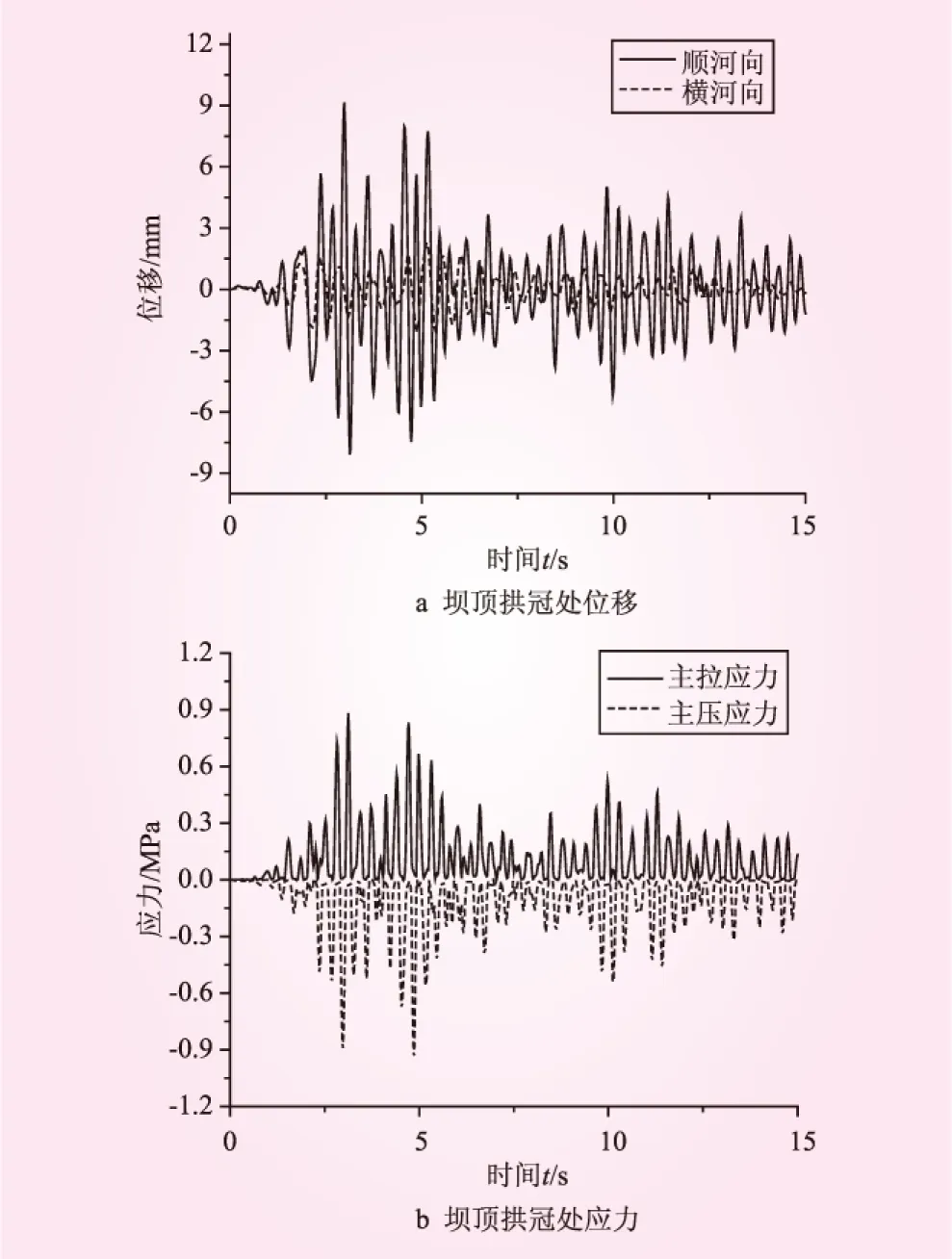
图7 空库状态下拱坝的位移和应力响应(粘弹性地基模型)
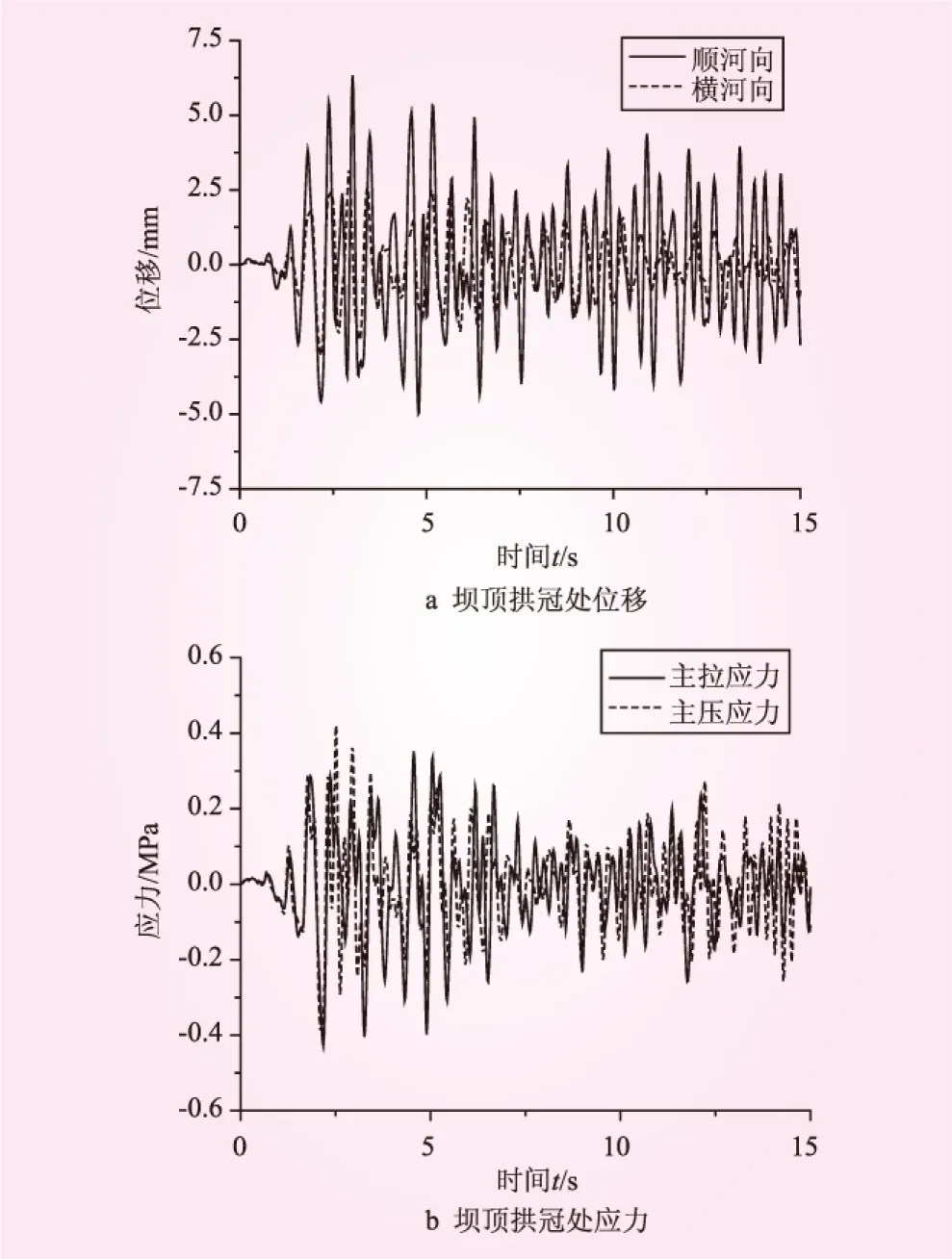
图8 半库水状态下拱坝的位移和应力响应(粘弹性地基模型)
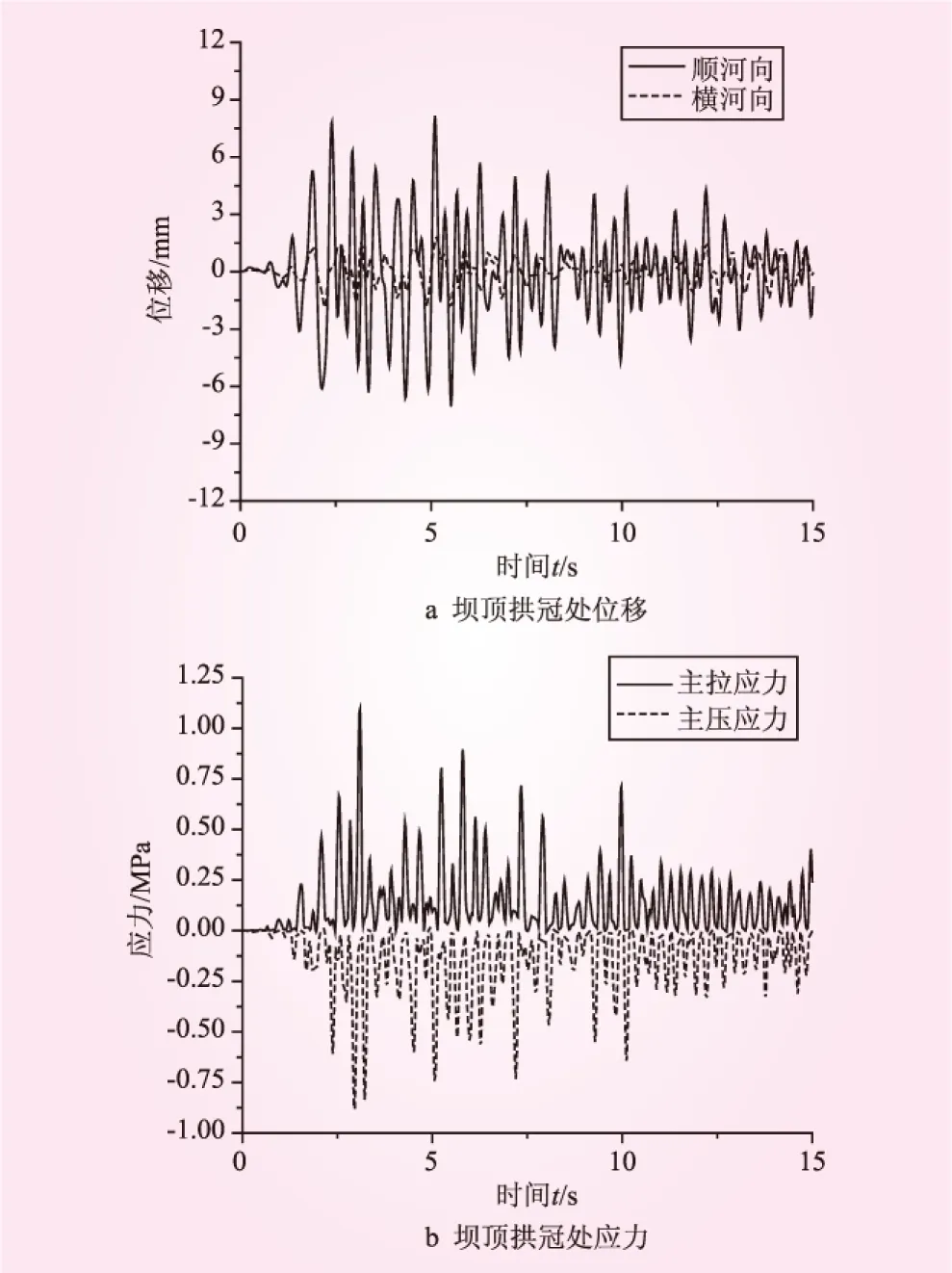
图9 满库水状态下拱坝的位移和应力响应(粘弹性地基模型)
3.2.2 粘弹性地基模型计算结果分析
图7~图9给出了空库、半库水和满库水时采用粘弹性地基模型时拱坝坝顶拱冠处关键点位移和应力情况。空库时,坝顶最大位移 9.15 mm,拱顶最大拉应力0.88 MPa,最大压应力0.94 MPa。半库水时,坝顶最大位移6.34 mm,拱顶最大拉应力0.607 MPa,最大压应力0.59 MPa。满库水时,坝顶最大位移8.16 mm,拱顶最大拉应力1.095 MPa,最大压应力0.875 MPa。
从算例结果分析中,可以看出粘弹性人工边界产生的位移时程峰值较小,振动幅度较大。设置粘弹性人工边界优点在于控制了地震波在有限元模型边界上的反射,有效地吸收了地震波能量,并且合理地模拟了地震波在无限地基中的传播。相比之下,采用固定边界,由于地基刚度较大的因素,会导致位移值偏大,造成能量在边界的反射,这些都会影响有限元模型动力计算的精确性。
4 结 论
本文结合ANSYS软件的参数化语言功能编制了模拟粘弹性人工边界以及地震荷载输入的程序。结合工程实例,建立了“库水-拱坝-地基”联合作用的有限元模型,通过施加粘弹性边界并输入相应地震动,分析了无限地基辐射阻尼的影响,得出结论如下:
(1)设置粘弹性人工边界能够控制地震波在有限元模型边界上的反射,并且很好地吸收了地震波能量,因此,粘弹性人工边界更符合实际地模拟了地震波在无限地基中的传播过程。
(2)考虑辐射阻尼效应,能够合理地计算出拱坝坝体地震响应。算例分析表明,粘弹性边界产生的位移时程峰值较小,波动幅度较大,其原因在于设置粘弹性人工边界条件,使得减少了能量在边界的反射,提高了有限元模型动力计算的精确性。
[1]ZHANG Chuhan, WOLF J P. Dynamic soil-structure interaction: current research in China and Switzerland[M]. Amsterdam: Elsevier, 1998.
[2]WOLF J P, SONG Chongmin. Finite-element modeling of unbounded media[M]. England: John Wiley & Sons, 1996.
[3]杜修力, 赵密, 王进廷. 近场波动模拟的应力人工边界条件[J]. 力学学报, 2006, 38(1): 49- 56.
[4]廖振鹏. 工程波动理论导论[M]. 北京: 科学出版社, 2002.[5]LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J]. Journal of Engineering Mechanics, 1969, 95(1): 759- 877.
[6]DEEKS A J, RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, 1994, 120(1): 25- 42.
[7]刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法[J]. 土木工程学报, 1998, 31(3): 55- 64.
[8]杜修力. 局部解耦的时域波分析方法[J]. 世界地震工程, 2000, 16(3): 22- 26.
[9]王振宇. 大型结构-地基系统动力反应计算理论及其应用研究[D]. 北京: 清华大学, 2002.
[10]杜修力, 赵密. 基于黏弹性边界的拱坝地震反应分析方法[J]. 水利学报, 2006, 37(9): 1063- 1069.
(责任编辑 王 琪)
Effects of Different Foundation Model on the Dynamic Response of Arch Dam
LI Shushan, LIU Zujun, JIA Mingxiao, XIE Wei
(North China University of Water Conservancy and Hydroelectric Power, Zhengzhou 450045, Henan, China)
Based on viscous-spring artificial boundary theory and wave field decomposition method of ground motion, the program for simulating viscous-spring artificial boundary and seismic load is developed by using the parametric language function of ANSYS software. Combined with practical arch dam engineering, the finite element model of dam-reservoir-foundation is established. Through implementing the viscous-spring artificial boundary and inputting corresponding seismic motion, the effects of radiation damping are analyzed. Compared with the calculation results of massless foundation model, it is found that the seismic response of dam will be in line with actual situation when the effect of radiation damping is considered. So the foundation model should be reasonably selected in seismic analysis of actual projects.
arch dam; dynamic response; viscous-spring artificial boundary; massless foundation
2016- 12- 28
贵州省水利厅科研项目(2012KT094);水利部堤防安全中心开放基金(201404)
李树山(1977—),男,辽宁绥中人,副教授,硕士,从事水工结构性能理论与试验研究.
TV642.4
A
0559- 9342(2017)08- 0056- 06
