测量机器人在一井定向中的应用及精度分析
2017-09-03胡玉祥熊文辉张洪德
胡玉祥,熊文辉,张洪德
(青岛市勘察测绘研究院,山东 青岛 266032)
测量机器人在一井定向中的应用及精度分析
胡玉祥*,熊文辉,张洪德
(青岛市勘察测绘研究院,山东 青岛 266032)
一井定向作为联系测量的基本手段,已得到了广泛应用,但传统钢尺量距的方式费时、费力。本文结合现代高精度测量机器人,分析了测量机器人替代钢尺量距的可行性,同时探讨一井定向的误差源,并对其进行精度分析。通过青岛地铁某竖井实际验证,使用测量机器人得到的定向边中误差分别为±12.2″、±9.9″,完全满足地铁建设规范要求。
一井定向;测量机器人;钢尺量距;误差源;精度分析;青岛地铁
1 引 言
一井定向作为地下隧道工程常用的联系测量手段,已经得到了广泛的应用[1]。由于单个竖井空间有限、环境较差、影响因素较多,导致一井定向实际操作过程中定向精度较差[2]。本文在已有竖井联系测量的基础上,结合现代高精度的测量机器人测角、量距,分析了测量机器人代替钢尺量距的可能性,结合常见的误差源,对一井定向的精度进行了分析。结合青岛地铁自身特点,通过实例验证了一井定向的精度和应用的可行性。
2 一井定向理论
一井定向就是在立井井筒中悬挂两根钢丝垂球线,在地面上利用地面控制点测定两垂球线的平面坐标及其连线方位角,在井下使用测量仪器测角量边把垂球线与井下起始控制点连接起来,通过计算确定井下起始控制点的坐标和方位角。一井定向测量工作分为投点(在井筒中下放钢丝)和连接测量两项工作。
2.1 投点
投点时,通常采用单重投点法(即在投点过程中垂球的质量不变)。单重投点可分为单重稳定投点和单重摆动投点两类。单重稳定投点是将垂球放在水桶内,使其基本上处于静止状态,只有当井筒中风流、滴水很小、垂球线基本稳定时才能应用。单重摆动投点是让钢丝自由摆动,用专门的设备观测其摆动,从而求出它的静止位置并加以固定。
由地面向井下投点时,由于井筒内气流、滴水等影响,导致井下垂球线偏离地面上的位置,该线量偏差e称为投点误差,由此而引起的垂球连线的方向误差θ(如图1所示)称为投向误差。其中误差为:
(1)
式中:c—两钢丝之间的距离。
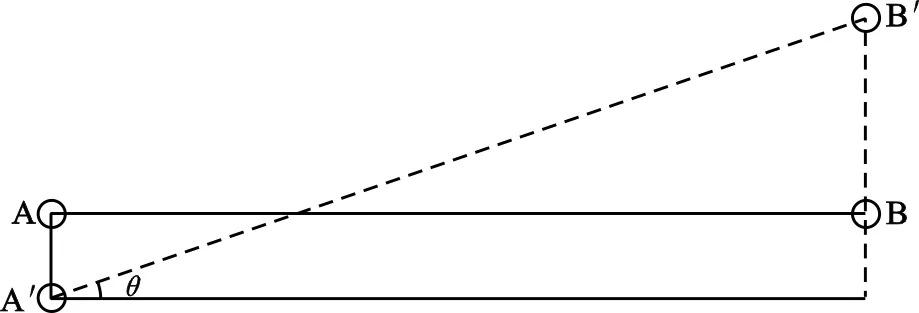
图1 投点误差与投向误差
2.2 连接测量
连接测量采用连接三角形法(如图2所示)。C和C′称为井上下的连接点,A、B点为两垂球线点,从而在井上下形成以AB为公用边的三角形ABC和三角形A′B′C′。
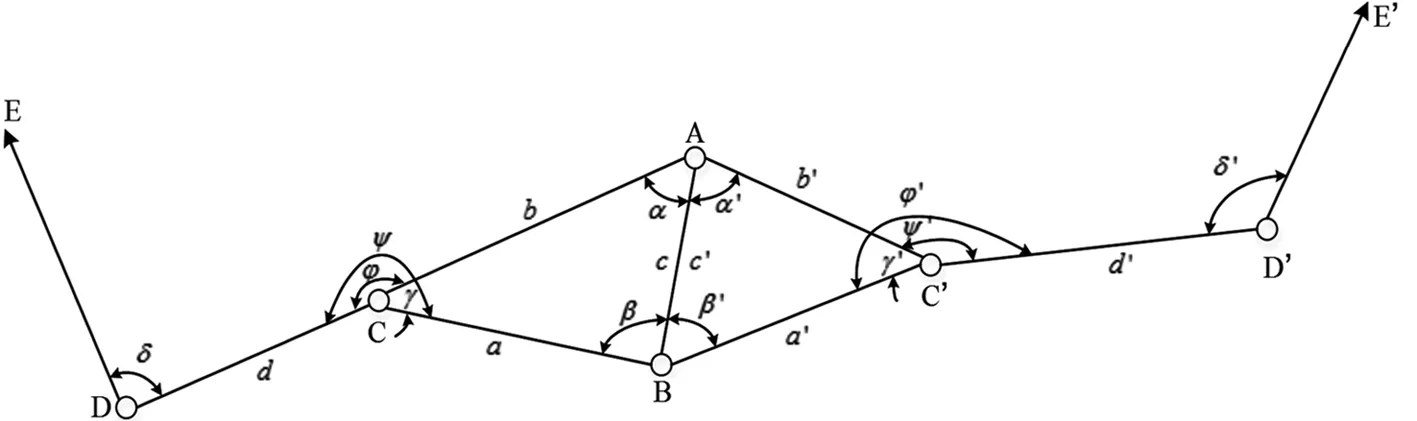
图2 连接三角形示意图
连接测量时,在连接点C和C′处按测回法测量角度φ、φ′、γ、γ′。同时丈量井上下连接三角形的6个边长a、b、c、a′、b′、c′。
内业计算时,首先对全部记录进行检查,然后对边长加入各项改正,按下式解算连接三角形各未知要素。即:
(2)
计算出的α、β角应满足α+β+γ=180°。因计算α、β角时数值凑整误差的影响,上述条件可能会不满足,若存有微小的残差时,可将其平均分配给α和β。另外,计算时应对两垂球线间距进行检查。设c丈为两垂线间距离的实际丈量值,c计为其计算值,则:
(3)
若地面连接三角形中d<2 mm、井下连接三角形中d<4 mm,可在丈量的边中加入改正,消除其差值。
在对各边长加入各项改正后,可依照D→C→A→B→C′→D′顺序构成支导线,按一般导线计算即可。
3 一井定向精度分析
由图2可知,井下导线起始边C′D′的方位角αC′D′可用下式计算:
αC′D′=αDC+φ-α+β′+φ′±4×180°
(4)
方位角αC′D′的误差就是定向误差,以mαC′D′表示。它除了包括计算中所用到的各角度误差外,还有投向误差θ。因此,总的定向误差为:
(5)
3.1 投向误差分析
如图3所示,A0、B0为垂球线在地面上所处位置,假设在投点时,B0点没有误差,而A0点有一线量误差eA,由图3可知,由此引起的投向误差为:
(6)
A0、B0—垂球线在地面上的位置;Ai、Bi—垂球线在定向水平上偏斜后的某一位置;
eA、eB—A0、B0在定向水平上的投点线量误差;φi—垂球线的偏斜方向与两垂球线联线方向的夹角;θi—垂球线在某一偏斜情况下所引起的投向误差;c—两垂球线之间的距离。

图3 垂球线的投向误差
实际上,即使在相同的eA条件下,投点线量误差的方向可能偏向任何一方,即投点后的位置可在以A0为圆心,以eA为半径的圆周上的任意一点,因而可得:
(7)
同理可得:
(8)
若两根垂球线的投点条件相同,即认为eA=eB=e,则总的投向误差为:
(9)
3.2 垂球线处角度误差分析
当α≈0°,β≈180°(或α≈180°,β≈0°)时,则各测量元素对于垂球线处角度的精度影响很小。因为此时
tanα≈0,tanβ≈0,cosα≈1,cosβ≈-1
垂球线处角度误差为[3]:
(10)
3.3 连接角误差分析
如图4所示,A和B为垂球线,CD为地面连接边。
假设仪器在连接点C上的对中有线量误差eT而对中在C1点上,则连接边就成了C1D。
可得中误差[3]:
(11)

图4 连接点上的对中误差
其次,在连接测量时,还要考虑到D点上的觇标对中误差meD,即:
(12)
因此,在C点连接角φ的误差,对连接精度的影响为:
(13)
当eT=eD=e时,则:
(14)
4 实例与分析
青岛地铁某施工竖井位于市区某车流密集地段,井深约 36.43 m,竖井井筒设为长方形,对角线长约 10 m,根据实际情况,在井筒对角线方向自由悬挂两根吊垂线,并将下端重锤浸入油桶中减小振动(如图5所示)。采用徕卡TS30测量机器人(标称精度:±0.5″、0.6+1×D,D为边长,以km为单位)测量角度、距离。为了更好地测量距离,在两钢丝上粘贴专有的徕卡反射片[5,6],距离和角度均测4个测回。
本实例测量如图5所示,在地上JJD观测方向JD1022和两根钢丝GSJ、GSY,方向HSJM2作为检核;在地下LSD1观测两根钢丝GSJ、GSY和方向HSL1-1、HSL1-2;同时测量JJD、LSD1与两钢丝反射片的距离。同时采用经检定的钢尺分别测量a、b、c、a′、b′、c′。本文首先采用间接平差方法分别对“TS30+反射片”和钢尺量距两种方式求取各点方位角、坐标较差,然后对一井定向总误差进行分析。
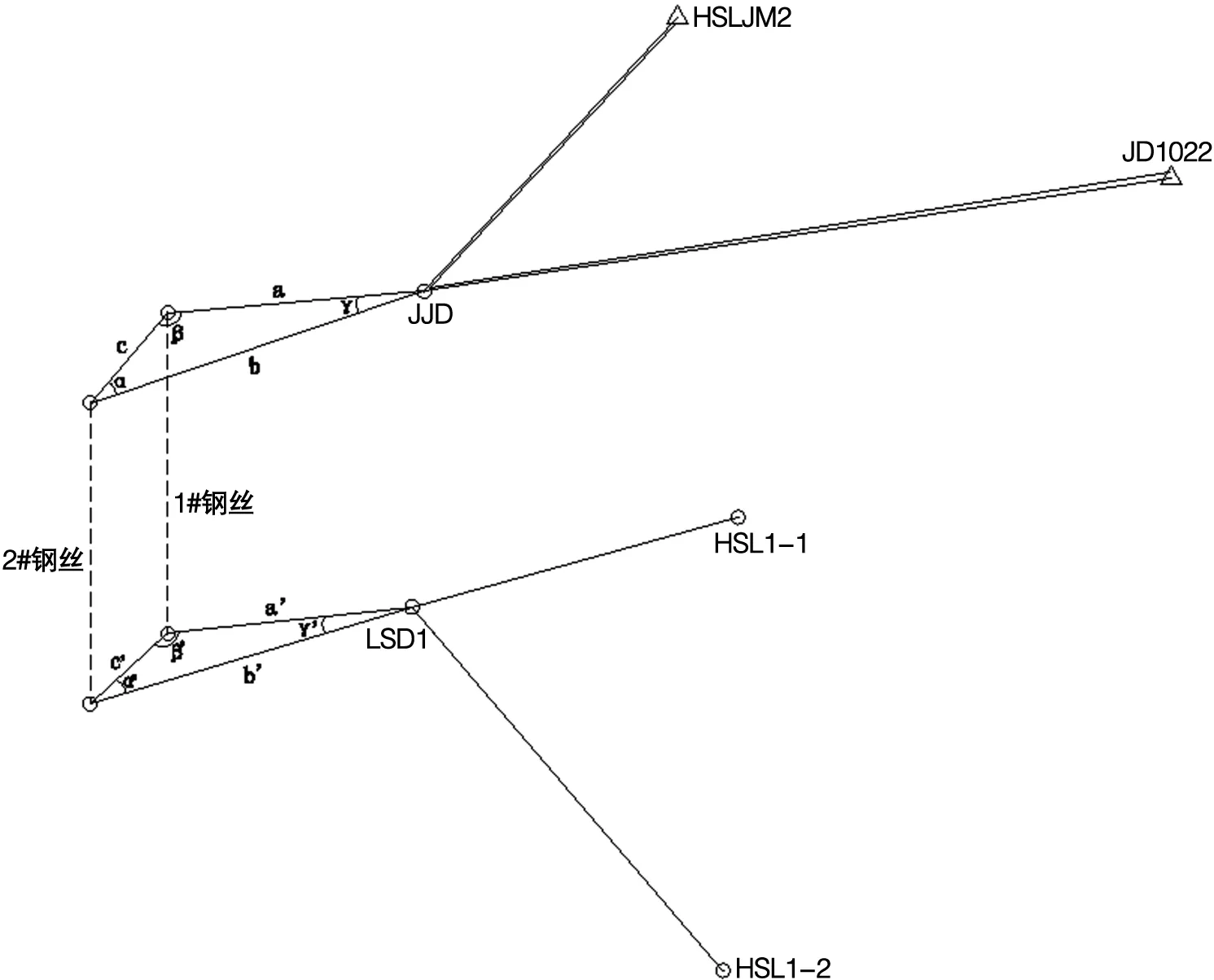
图5 一井定向连接示意图
(1)“TS30+反射片”和钢尺量距对比

TS30与钢尺测量边长对比表 表1

方位角较差表(“TS30+反射片”和钢尺量距分别平差后) 表2
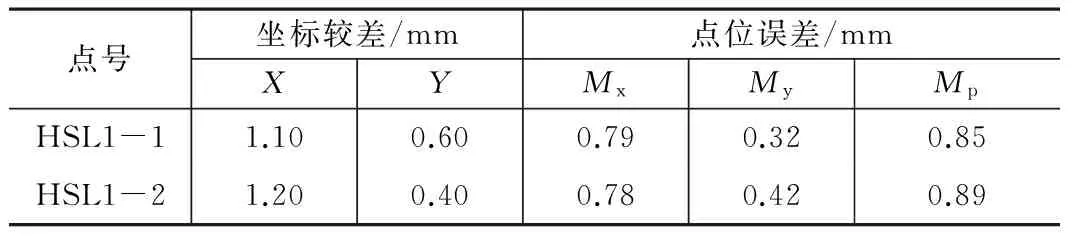
坐标较差表(“TS30+反射片”和钢尺量距分别平差后) 表3
①从表1可以看出,使用“TS30+反射片”测出的距离经改化和钢尺量出的距离较差最大为 -2.2 mm;②从表2可以看出,使用“TS30+反射片”测出的距离经改化和钢尺量距分别平差后井下起始边方位角较差为1.1′;③从表3可以看出,使用“TS30+反射片”测出的距离经改化和钢尺量距经平差后井下起算点的点位中误差较差分别为 0.85 mm、0.89 mm。
(2)一井定向总误差分析
定向测量采用TS30测量机器人,从实测角度精度分析求得测角中误差为±1.4″,测角方法误差为±2.5″。井上仪器对中误差及觇标对中误差为 0.8 mm,井下仪器对中误差及觇标对中误差为 1 mm,投点误差为 0.9 mm,由式(5)可得定向边的中误差:MαLSD1-HSL1-1= ±12.2″、MαLSD1-HSL1-2=±9.9″。满足《城市轨道交通工程测量规范》的精度要求。
5 结 论
结合现代高精度测量机器人TS30在城市地铁中的应用,本文对“TS30+反射片”量距和钢尺量距两种方式进行了对比分析,同时探讨一井定向的误差源,并进行精度分析。通过青岛地铁某竖井分析表明,使用TS30测角、量距求得的竖井定向边中误差分别为 ±12.2″、±9.9″,完全满足《城市轨道交通工程测量规范》要求。因此,对于城市地铁而言,使用“TS30+反射片”量距方式完全可以替代传统的钢尺量距方式,能给测量工作带来更多便利。
[1] 张正禄. 工程测量学[M]. 武汉:武汉大学出版社,2002.
[2] 张国良,朱家钰,顾和和. 矿上测量学[M]. 徐州:中国矿业大学出版社,2001.
[3] 郑文华. 地下工程测量学[M]. 煤炭工业出版社,2011.
[4] GB50308-2008. 城市轨道交通工程测量规范[S].
[5] 徐茂林,杨风云,李冬梅等. 利用一井定向资料完成两井定向的方法[J]. 测绘通报,2002(1):29~31.
[6] 温建生. 一井与两井定向并用测量的探讨[J]. 山西建筑,2001(6):142~143.
[7] 唐军,宋冬梅,李建平. 浅谈矿上联系测量中的一井定向、两井定向测量的异同点[J]. 西部探矿工程,2010(5):133~135.
[8] 刘建伟,师军良. 一井定向在地铁隧道中的应用[J]. 内江科技,2009(6):7~12.
Application and Accuracy Analysis of Measuring Robot in One-shaft Orientation
Hu Yuxiang,Xiong Wenhui,Zhang Hongde
(Qingdao Geotechnical Investigation and Surveying Institute,Qingdao 266032,China)
As a basic means of connection survey,one-shaft orient has been widely used,but the traditional steel tape measuring is time-consuming and strenuous. In this paper,combined with the modern high precision measurement robot,the feasibility of measuring robot instead of steel tape measuring is analyzed,the error sources and precision analysis is also discussed. According to the actual verification of a shaft in Qingdao metro,the error of the directional edge is respectively ±12.2″、±9.9″,completely meeting the requirements of metro construction.
one-shaft orientation;measuring robot;steel tape measuring;error source;accuracy analysis;Qingdao Metro
1672-8262(2017)04-142-04
P258
A
2016—12—14
胡玉祥(1988—),男,硕士,工程师,主要从事GNSS数据处理与应用、城市轨道交通测量研究工作。
