一种基于切换迟滞的LTE自适应计时水平切换算法

胡 霞

(湖南邮电职业技术学院，湖南 长沙 410015)

一种基于切换迟滞的LTE自适应计时水平切换算法

胡 霞*

(湖南邮电职业技术学院，湖南 长沙 410015)

针对LTE固定计时切换算法存在的缺点，提出了一种自适应计时切换算法.该算法依据当前移动台与原服务小区的距离di及rank，ram和p这3个可变常数，计算其实时的切换计时值T，从而实时改变切换等待时间.仿真结果表明：采用固定计时切换算法，且计时值T设置偏大时，移动台需移动到离原服务小区较远的地方才能发生切换，此时移动台接收原服务小区的信号强度很差；而自适应计时切换算法不仅能消除乒乓效应，减少平均切换次数，且切换时拥有较好平均信号强度，切换位置更集中合理，总体性能达到最佳效果.

LTE；自适应；计时；水平切换；切换迟滞

一种好的移动台切换算法需同时兼顾好切换次数和切换时服务小区信号强度.在仅基于移动台接收服务小区的信号强度，而不考虑切换迟滞和切换计时的移动台切换算法中，当移动台进入同系统服务小区和其邻小区的重叠覆盖区域时，由于移动台从两个小区所接收到的信号强度非常接近，很容易造成移动台在两个小区间的乒乓切换，从而使移动网络的负载大大增加.为降低乒乓切换影响，当前2G/3G移动系统一般的做法是提高切换的门槛条件，即采用切换迟滞的固定计时切换算法.这样，虽然移动台乒乓切换的机会大大减少了，但切换时移动台可能已移至离原服务小区较远的地方，因而使得移动台发生切换时所接收到的原服务小区的信号强度很弱，甚至切换失败，从而增加了切换掉话率.于是，针对当前各国正大力推出的4G移动系统以及未来将推出的5G移动系统，文章提出了一种切换改进算法，即自适应计时切换算法.自适应计时切换算法不仅能消除乒乓切换，减少移动台平均切换次数，而且移动台发生切换时对原服务小区有较好的平均接收信号强度，移动台的切换位置更集中合理，因而自适应计时切换算法优势更明显[1-2].

1 固定计时切换算法

1.1 基于固定迟滞的固定计时切换算法

固定计时切换算法(Fixed Timer Handoff algorithm, FTHO)可用来降低移动台的乒乓切换效应[3-5].若服务小区的切换计时器为T，在第(K-T+1)th时刻取样时，如果移动台收到邻小区的信号强度比服务小区的信号强度加上迟滞值h还要强，则启动计时器，如果经过连续T次取样都满足此条件，则在第Kth取样时刻进行切换，切换的判别式：

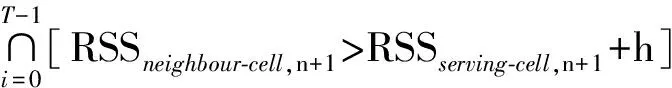
(1)

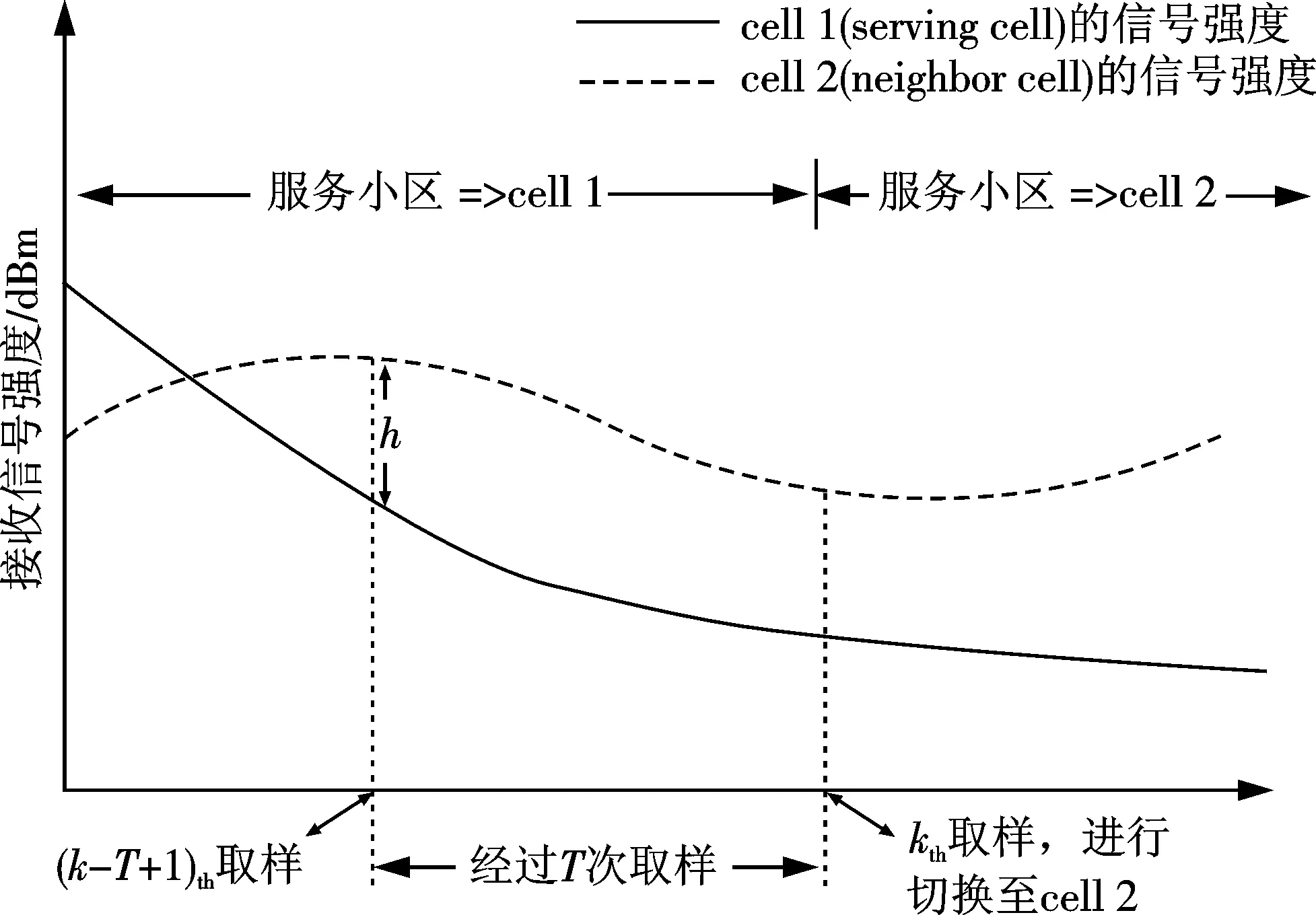
图1 固定计时切换算法原理图Fig.1 Fixed timing switching algorithm schema

切换的原理如图1所示，即连续T次取样判断式(1)都成立时才会进行邻小区的切换，移动台才会从服务小区cell1切换到邻小区cell2，如果从第(K-T+1)th时刻取样开始到第Kth取样时刻结束前其中有任何一次从cell2取样的信号强度没有大于cell1的信号强度加上迟滞值h时，计时器就会重新开始计数.

显然，如果计时值T设置偏大，切换越难，虽然切换次数减少了，乒乓效应也降低了，但是，移动台可能已移动到离服务小区cell1偏远的地方才发生切换，此时移动台与服务小区连接的信号质量已经很差.

固定计时切换算法程序如下：

(1)移动台测量服务小区Ps-i和邻小区信号强度Pn-i；

(2)移动台计算Pn-i是否大于Ps-i+h，如否，将ii+1转到1，重新测量；如是，转到3；

(3)启动切换计时器T开始计时，在第(K-T+1)th时刻取样开始到第Kth时刻是否有Pn大于Ps+h，如有，则转到1，如否，则转到4;

(4)移动台切换到邻小区.

1.2 基于自适应迟滞的固定计时切换算法

在固定迟滞的FTHO切换算法中[6-9]，由于没有灵活考虑移动台离服务小区的距离因素，其切换的迟滞值是不变的，移动台发生切换的质量仍然不高，于是人们又提出了自适应迟滞切换算法(Adaptive Hysteresis Handoff algorithm, AHHO)[10].AHHO切换算法即移动台根据其与服务小区距离的不同来改变其实时的迟滞值，其实时的迟滞值h的计算公式：

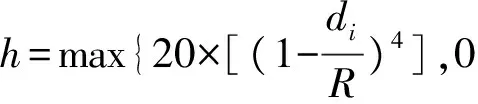
(2)

式中，h表示实时的迟滞值;di表示移动台第i次测量到的与基站服务小区的距离;R表示基站服务小区的半径.从式(2)可看出，当移动台与服务小区的距离较近时，迟滞值大，切换的概率低;反之，当移动台与服务小区的距离较远时，迟滞值小，切换的概率高.这样，切换的位置基本上被控制在小区的边界.

2 自适应计时切换算法

自适应迟滞固定计时切换算法与固定迟滞切换算法相比虽可有效改善移动台在两个小区边界处的乒乓切换，但是其切换率仍然过高，而且当移动台位于3个小区的交界处时，由于移动台从3个小区所收到的信号强度相当接近，自适应迟滞值H接近于0，此时无法解决乒乓切换[11-12].而且可能因其固定的切换计时偏长，使得切换时移动台接收原服务小区的信号很弱，甚至造成掉话.因此，针对固定计时切换算法仍然存在的缺点，本文提出一种新的切换算法，即自适应计时切换算法(AdaptiveTimerHandoffalgorithm，ATHO).

ATHO切换算法基本原理如下：当移动台离服务小区越近，移动台接收原服务小区的信号越强，所计算出的切换计时值T越大，切换的几率就越低；反之，当移动台离服务小区越远，所计算的计时值T越小，切换的几率就越高.

ATHO切换算法的切换判断式同式(1)，但是其计时T会随着移动台与服务小区之间距离的变化而变化，其计时T计算公式为：

(3)

式中，round为四舍五入函数;max为对括号内的两值取较大值函数;di为移动台第i次测量点与服务小区的距离，是T计算公式中唯一的变量;rank,ram和p均为可变常数，其中rank为对应切换计时的最大值，ram为切换计时变为1时移动台离服务小区的对应最小距离，p为距离相对比指数，3个常数变化对切换计时T的影响如图2所示.

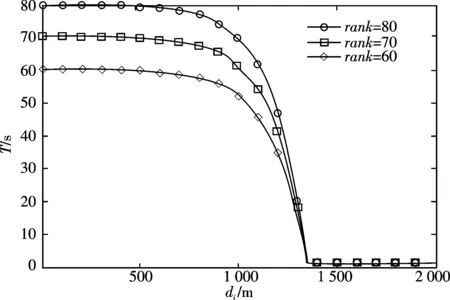
(a)ram=1 350，p=8时rank变化对计时T的影响

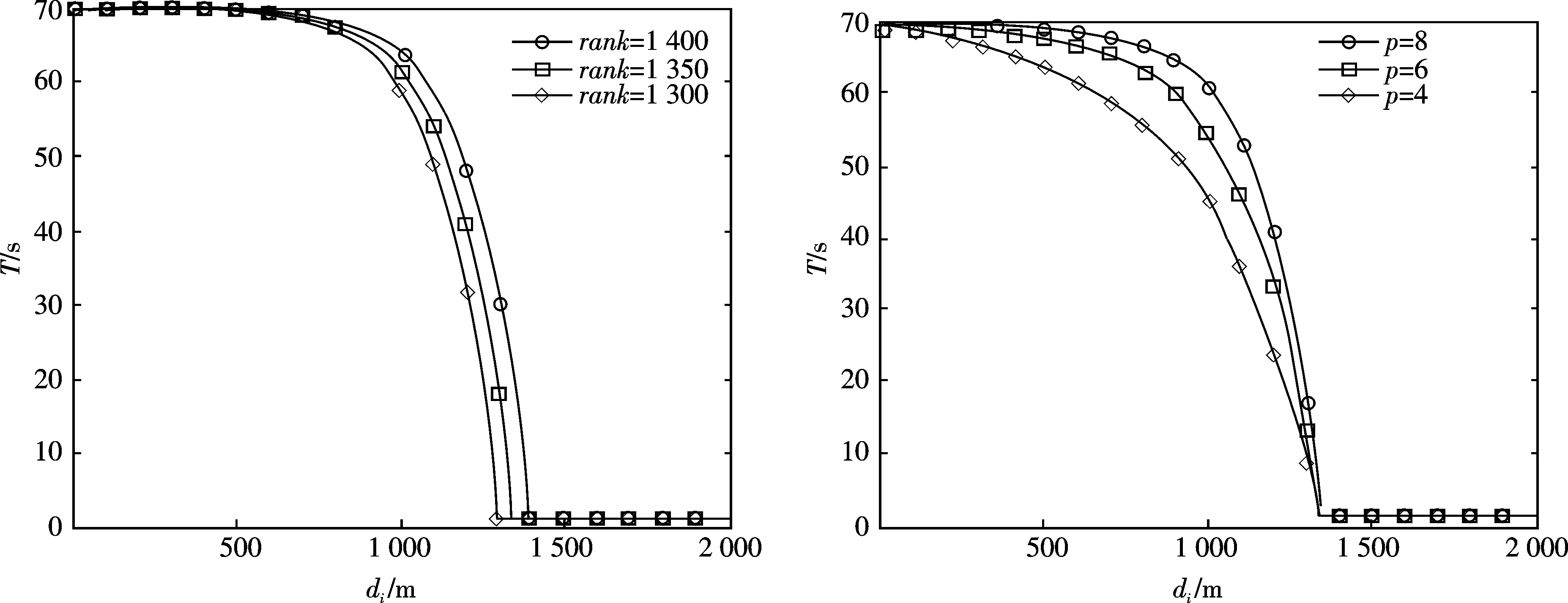
(b)rank=70，p=8时ram变化对计时T的影响 (c)rank=70，ram=1 350时p变化对计时T的影响图2 自适应计时切换rank，ram，p常数变化对计时T的影响Fig.2 Adaptive timing switch rank, ram, P changes in the timing of the impact of T

由图2(a)可知，rank在di较小时对T的影响较大，且rank越大，计时值T越大，rank决定了di等于0时T的最大值.随着di增大，不管rank为多少，T都会减小，最终T都会在di等于ram时下降到1，图中由于ram设为1 350，所以图中的3条线的T都会在di等于1 350时下降到1.由图2(b)可知，随着di增大，不管ram为多少，T都会减小，而最后T都会在di等于ram时下降到1.而且，当di较小时，ram变化对T的影响较小，当di较大时，ram变化对T的影响较大，但在di很大时，ram变化对T的影响消失.同时还可以看出，ram越大，T会在di越大时下降到1，如图中ram=1 400的曲线，其T会在di为1 400时下降到1，并且当di大于1 400时，T会保持为1.由图2(c)可知，p决定了曲线的垂直程度，p值越大则曲线越垂直，图中由于ram=1 350，其T值都会在di等于1350时下降到1.因此，3个常量rank,ram和p变化情况下计时T都会随着di增大而减少.

3 不同切换算法性能仿真比较

3.1 仿真条件设置

为比较不同水平切换算法切换性能好坏，假设移动台每次都是从cell1服务小区位置出发，向cell2匀速直线前进，通过电脑多次模拟仿真来统计平均切换次数、切换时移动台接收cell1的平均信号强度、第一次切换时离cell1的平均距离来做比较分析.

移动台从cell1和cell2小区接收到的信号强度公式分别为：

RSScell1=K1-10×K2×log(di)+￡i，

(4)

RSScell2=K1-10×K2×log(D-di)+￡i，

(5)

在式(4)和式(5)中K1表示基站发射功率；K2表示路径损耗指数；D表示cell1与cell2间的距离；di表示移动台在第i次取样时与cell1的距离；￡i表示第i次取样时阴影效应对移动台信号强度影响.

具体仿真条件如表1所示.

表1 系统模拟仿真参数表

3.2 自适应计时切换算法rank,ram,p常数变化对切换位置的影响

图3是自适应计时切换算法rank,ram,p常数变化对切换位置影响情况图.

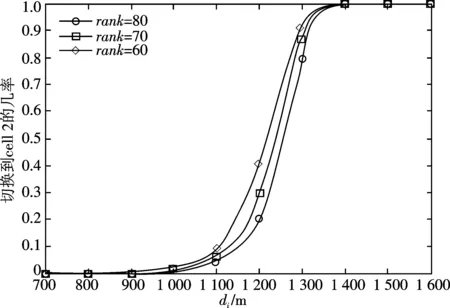
(a)p=8，ram=1 350时rank变化对切换位置的影响

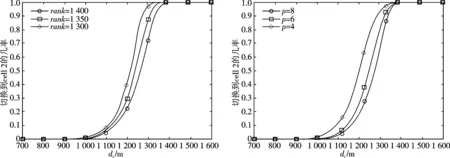
(b)p=8,rank=70时ram对切换位置的影响 (c)rank=70,ram=1 350时p对切换位置的影响图3 rank，ram和p常数变化对切换位置影响的几率累积分布函数Fig.3 Probability cumulative distribution function of rank, ram, p constant variation on switching position

图3(a～c)分别为rank,ram及p3个参数变化对切换位置影响的几率累积分布函数.由图3(a)可知，rank越大，切换的位置几率累积分布曲线越接近cell2，即切换的位置会离服务小区cell1越远，这是因为当di小于或等于ram时，rank越大，T越大所造成.从图3(b)可看出，当di较小时，由于ram对T的影响较小，所以图中的3条线很接近.但是，随着di增加，ram对T的影响才逐渐明显，此时ram越大，切换的位置几率累积分布越接近cell2，也是因为ram越大，T越大所造成.从图3(c)可知，当p增加时，切换位置的几率累积分布曲线斜率上升，即曲线更接近垂直.同样可看出，p值越大，切换的位置几率累积分布越接近cell2，且切换位置越集中.但是，会使得移动台的切换跟接收信号强度的关系变小，影响切换判断的依据反而变成di，那么基于信号强度的水平切换就会变成基于位置判断的水平切换.

3.3 固定计时和自适应计时切换算法对切换几率密度分布、切换累积几率分布影响比较

在图4和图5中，比较了T=5及T=10时的FTHO算法和ATHO算法的切换几率密度分布和切换累积几率分布情况，其中ATHO算法所采用的参数T为式(6)中所对应.

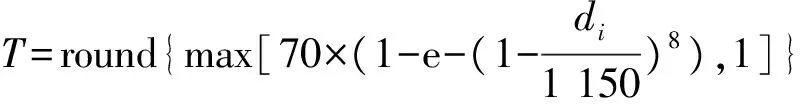
(6)

由于di切换几率大多集中在800～1 400 m，因此两图都只选择800～1 400 m距离来观察切换几率.且两图中所用自适应迟滞切换所用的迟滞值h都使用式(1)计算，以此来观察不同切换算法的几率分布情况.

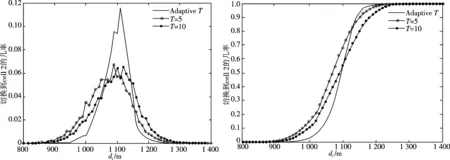
图4 切换几率密度分布(PDF)比较 图5 切换累积几率分布(CDF)比较Fig.4 Comparison of switching probability density distribution (PDF) Fig.5 Comparison of switching cumulative probability distribution (CDF)

从图4和图5可看出，移动台大约在距离服务小区1 000～1 150 m间切换.当采用FTHO,且T=5时，由于计时较小，图中的切换几率会相对偏向于cell1，也就是比较早切换.太早切换虽然切换时服务小区的信号比较强，但容易造成乒乓效应.当T=10时，由于计时变大，图中的切换几率会偏向于cell2，也就是比较晚切换.太晚切换虽然可降低乒乓切换次数，但会降低切换时服务小区的信号强度.相比FTHO，ATHO切换算法能更有效地将切换位置控制在此范围的一个小区域内，既达到了降低乒乓效应，又兼顾了切换时原服务小区的信号强度.

3.4 不同切换算法平均切换次数、切换时信号强度及切换位置比较

表2和表3为采用ATHO与FTHO切换算法在不同迟滞值时的切换次数和接收信号强度仿真性能比较.很显然，采用FTHO算法，当迟滞值增加，在减少平均切换次数的同时，也会降低切换时的信号强度，所以选择迟滞值时也有一定的取舍.而通过比较FTHO切换算法在T=5和T=10时的性能可知，固定计时值大时，虽然可减少平均切换次数，但切换时的信号强度却降低了.反之,固定计时值较小时,虽然切换次数多，但切换时信号强度较强.而采用ATHO切换算法，随着移动台与服务小区的距离越远，计时值降低，将切换的几率集中在两个小区的交界或服务小区的边界.由数值显示，在平均切换次数及切换时信号强度方面都优于T取不同值时的FTHO切换算法.

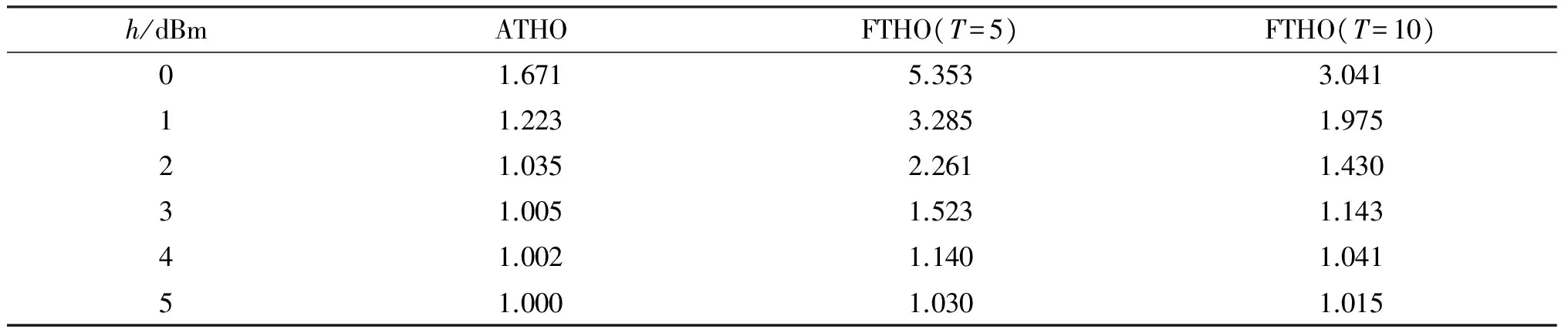
表2 平均切换次数比较

表3 切换时信号强度(dBm)比较

表4为采用ATHO切换算法和FTHO切换算法在不同迟滞值时，其第一次切换位置的仿真性能比较.从表4可看出，当迟滞值h越大时，切换的位置距离cell1越远，当比较两个固定计时值时，T越大，则切换时离cell1的距离会越远.观察T为5时的FTHO情况，当迟滞值h小于4 dBm时，平均切换位置比ATHO的切换位置更接近于cell1，但当迟滞值h大于或等于4 dBm时，其切换时比ATHO距离cell1更远了；而当T为10时的FTHO情况，则在迟滞值h大于或等于1 dBm时，移动台切换时离cell1的距离就超过了采用ATHO切换算法时的距离.

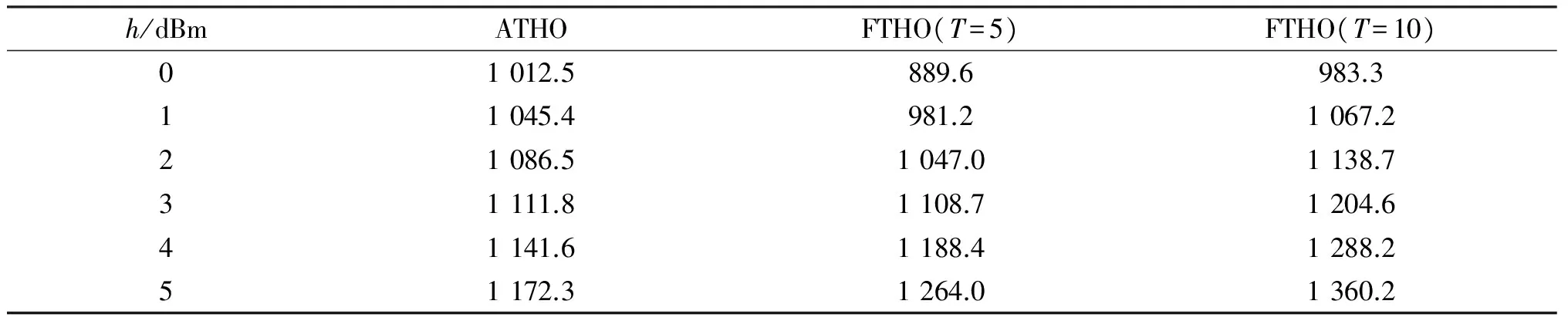
表4 切换位置(m)比较

所以对于FTHO切换算法，切换的位置比较容易受到迟滞值h的影响，切换几率的分布也比较广；而对于ATHO切换算法，切换几率较集中于两个小区的交界与cell1的边界中，所以切换的位置较不容易受迟滞值影响，也因为切换位置几率较集中，所以有时候虽然平均切换距离较远，但仍可得到较强的切换平均信号强度.

表2～表4的仿真结果证明：采用ATHO切换算法能够将切换几率集中在两个小区交界到服务区的边界，改善采用FTHO切换算法所造成的切换时接收服务小区信号强度差的缺点.

表5为使用自适应迟滞，不使用计时、使用固定计时与自适应计时的切换性能仿真比较.由表5可见，只使用自适应迟滞加平均滤波器，虽然切换时信号强度比固定计时时强，且第一次切换更靠近cell1小区，但是平均切换次数却高于固定计时切换.这是因为固定计时切换算法需要经过多次的取样判断才会进行切换，比起使用平均滤波器不使用计时的自适应迟滞切换算法，更可降低乒乓效应，减少切换次数.但是计时切换算法移动台切换时平均信号强度却比较低，所以当使用固定计时算法，计时值的大小就有所取舍.仿真结果也证实自适应性计时切换算法改善了这个缺点，不仅消除了乒乓效应，也使得切换时拥有较好的信号强度.

表5 自适应迟滞与不同计时切换的性能比较

4 结束语

通过仿真比较了固定计时切换和自适应计时切换两种切换算法情况下移动台切换几率密度分布、切换累积几率分布、平均切换次数、切换位置、切换时平均信号强度等方面的性能差异，得出了自适应计时切换算法较固定计时切换算法的平均切换次数少、切换位置更集中合理、切换时平均信号强度强，总体性能更优越.

[1] HUANG Y F, HSU C W, GAO F B,etal. Performangce of adaptive vertical handoff in heterogeneous networks of WLAN and WCDMA systems[J].Proc of 5th International Conference on Networked Computing and Advanced Information Management (NCM2009), 2009(8):2012-2017.

[2] MAITRA M, AUKHERJEE A, SAHA D. Integrated interswitch cable and handoff cost minimizing heuristics for cell-to-switch assignment in wireless cellular networks[J].IEEE Transa Vehic Technol, 2008,58(9):5074-5082.

[3] HE F, WANG F, HU D. Distance and velocity assisted handoff decision algorithm in heterogeneous networks[J].Proc of Second International Coference on Future Generation Communcation and Networking (FGCN 2008)，2008(8):1509-1512.

[4] TAWIL R, PUJOLLE G, SALAZAR O. A vertical handoff decision scheme in heterogeneous wireless systems[J].Proc of 2008 IEEE Vehicular Technology Conference(VTC 2008), 2008(3):2626-2630.

[5] 谢显中，肖博仁，马 彬，等.代价函数权值可变的速度自适应的异构无线网络垂直切换算法[J]．电子学报，2011,26(10)：2417-2421.

[6] ROY S D. A timer based handoff algorithm for multi-cellular systems[J].Proc of 2008 Emerging Trends in Engineering and Technology (ICETET)Conference, 2008(7):819-822.

[7] SHU T, LIU M, LI Z C. A performance evaluation model for RSS-based vertical handoff algorithms[J].Proc of IEEE Symposium on 2009 Computers and Communications (ISCC 2009), 2009(7):271-276.

[8] INALTEKIN H, WICKER S B, MUNG C,etal. On unbounded path-loss models：effects of singularity on wireless network performance[J].IEEE J Selected Areas Commun, 2009,27(7):1078-1092.

[9] TIBREWALA A, PRAMANICK D, ROY S D,etal. Signal strength ratio based handoff algorithms for cellular networks[J].Proc of Annual IEEE 2008 India Conference (INDICON 2008)，2008(11):11-13.

[10] 吕莎莎，孙建伟，贾军营，等.基于群集移动节点的切换算法[J].计算机应用，2011,27(12)：3219-3222,3229.

[11] 罗 涛，吕子茹，姚 哲，等.WAVE系统中一种基于位置的切换算法[J].中国通信，2011,24(1)：95-101.

[12] 孙巍巍，苏寒松，滕友伟，等.3GPP LTE系统中结合位置预测的切换算法[J].计算机应用，2012,28(7)：1849-1851,1863.

(编辑 CXM)

An Adaptive Timer Handoff Algorithm Based on Handoff Hysteresis in LTE

HUXia*

(Hunan Post and Telecommunication Vocational College, Changsha 410015, China)

An adaptive timer handoff algorithm with respect to the shortcoming of fixed timer handoff algorithm in LTE was proposed. In the algorithm, the real-time handoff timer valueTwas calculated based on the distancedibetween current mobile station and original serving cell as well as three constant variables:rank,ramandp, thus changing the handoff waiting time in real time. The simulation results showed that the handoff occurs only when the mobile station needs to move to a far position from the original serving cell in the fixed timer handoff algorithm and larger set timer valueT, and the strength of signals

by the mobile station in the original serving cell is poor; however, in the adaptive timer handoff algorithm, the ping-pong effect can be eliminated, the average handoff times are reduced, the mean strength of signals at handoff is better, the handoff position concentrates rationally and the overall performance reaches to the optimal effect.

LTE; adaptive; timer; horizontal handoff; handoff hysteresis

10.7612/j.issn.1000-2537.2017.04.012

2017-03-08

湖南省教育科学“十三五”规划课题(ZJK016CZY065)

TP393.09

A

1000-2537(2017)04-0068-07

*通讯作者,E-mail：178839185@qq.com