基于人群到达规律的公共场所踩踏风险分析*
2017-09-03谢科范
曹 青,谢科范
(武汉理工大学 管理学院,湖北 武汉 430070)
基于人群到达规律的公共场所踩踏风险分析*
曹 青,谢科范
(武汉理工大学 管理学院,湖北 武汉 430070)
公共活动在丰富人们物质文化生活的同时,也易发生人群踩踏风险。人群踩踏风险一旦发生,造成的后果可能会十分严重。因此,监测、预警和预控人群踩踏风险已越来越引起公共活动组织与管理者的重视。通过对2016年归元寺春节祭祀活动进行数据分析,从微观上论证得出了城市公共场所人群到达服从泊松分布的结论,且发现人群到达呈现入口效应和最短距离效应,以此作为人群踩踏风险计算机模拟的参数设定依据,对优化和设计公共活动的踩踏防控预案方案,提升人群管控能力,降低人群踩踏风险有一定的参考意义。
人群踩踏;踩踏风险;人群密度;人群到达;泊松分布
一、问题的提出
随着社会的发展,人们的物质文化需求逐步提高,城市公共场所承载的公共活动数量也日益增长。公共活动在丰富人们的物质文化生活的同时,也容易诱发人群踩踏风险。由于人群踩踏风险的的致因具有潜在性,因此其预防预控有一定难度。踩踏事件一旦发生,有可能造成群死群伤的严重后果。例如,2011年1月14日、2013年10月13日发生在印度的两起踩踏事故,其死亡人数均超过100人。2014年12月31日上海外滩踩踏事故死亡人数也达到了36人。所以,对公共活动的人群踩踏风险进行分析并探讨相应的防控措施,便显得十分重要。
目前国内外对人群踩踏风险的研究主要分为实证研究和理论研究两个方面。实证研究主要是根据直接观察、摄影和录像分析等方式研究人群集聚与疏散特征。学者们大多是设定和验证不同国家、不同场景下人群密度、人流速度、出口宽度等因素之间的函数关系。例如,Hankin和Wright[1]调查了伦敦地铁中行人流动情况,描画了单向人流的速度和密度之间的关系。Fruin[2]调查了人行道的人群速度和人群密度的关系,给出了图示,并将人员步行流动状态分为从互不影响到严重滞留的六个等级。加拿大的Paul[3]通过实证数据提出了有效楼梯宽度、疏散人数和疏散时间的关系。Thompson和Marchant[4]将观察数据整理,并结合采用Fruin,Hankin等人的数据,总结分析了不同学者研究的人群密度和人群速度的经验关系。在国内,武汉大学的研究人员[5]采用流体力学的原理分析人群运动,并建立了人群密度、人群速度和人群流量之间的对数关系。张培红[6]总结分析了时间压力下不同位置的人群流动速度和人群密度的关系,并提出局部衰减系数概念。吕雷等人[7]对学校教学楼的人群密度和人群速度进行了实地记录。胡玉婷[8]运用2010年世博会的视频数据对人群的区域分布和人群运动轨迹形成规律进行了分析。
在理论研究方面,主要工作是对特定场景下的人群疏散策略进行建模与模拟。Lee和Hughes[9]基于Lighthill和Whitham[10]的研究提出了连续行人流运动模型。Dirk Helbing等人[11]在分析人群的互相作用力后提出了经典的社会力模型。之后的研究则大部分以该模型为基础,对其进行相应的优化和计算机模拟研究。如日本的Teknomo[12]在Helbing的基础上,对人群中个体之间的相互作用的“排斥力”进行了分析,并建立了相关的微观模拟模型。宋卫国[13]提出了一种考虑摩擦力与排斥力的人群疏散CA模型,该模型不仅可以较好地描述人员疏散中的典型现象,如拥挤、堵塞现象等,而且具有较高的运算效率。张青松等[14]则运用牛顿第二定律和经典“社会力”模型对人群中的个体受力进行了微观建模。
虽然许多学者已经研究分析了人群密度和人群踩踏风险的关系,但鲜有学者对人群达到与人群踩踏风险之间的关系进行研究。也有一些学者在人群踩踏风险的仿真模拟分析中假定人群进入仿真区域服从均匀分布[15-16]或者泊松分布[16],但是,对于人群进入仿真区域时是否确实遵循泊松分布,国内外缺少基于实际活动观测数据的实证研究。
基于此,作者对2016年武汉市归元寺春节祭祀活动的人群进行了现场观察,采集了视频数据。本文在此基础上运用统计方法和理论分析处理数据,从微观层面揭示城市公共场所人群到达的规律,并对人群踩踏风险与人群到达规律进行建模,为分析人群聚集风险提供参照。该研究成果可以作为人群踩踏事故触发与演化机理的计算机模拟参数设定依据,研究的结论可作为优化和设计公共活动方案,提升人群管控能力,降低人群踩踏风险的参考。
二、人群踩踏风险分析
(一)人群踩踏风险定义
本文中所说的人群踩踏风险是指城市公共活动中由于人群高度集聚、发生突发状况等多个因素综合作用,产生群死群伤的事故风险。
对于人群踩踏事故来说,人群踩踏风险Ri是风险发生可能性Fi和后果Ci的函数[17]:
(1)
虽然公共活动的种类和场所不尽相同,但是人群踩踏风险发生可能性函数可以近似为独立的几个阈值参数相互作用的函数。当阈值突破时,人群踩踏发生的可能性和后果上升,即人群踩踏风险上升。
人群踩踏风险发生的必要条件主要有:
(1)人群处于非正常情绪之中,例如恐慌或亢奋;
(2)人群处于高度密集状态,事故发生前,总体人群密度超过可接受阈值,部分人群密度极大地超过可接受阈值;
(3)发生人群踩踏的触发事件,如有人意外摔倒,争吵,惊跑[18]等等;
(4)人群移动无法受到有效的控制,人群中的个体呼救或警告广播等情况无法有效促使人流改变移动方向。
当满足上述必要条件个体越多时,人群踩踏风险发生的可能性越大。而当人群踩踏事故一旦发生,则人群疏散所需的时间就会增加,生态恶化的可能性会越大,人群踩踏事故造成的后果也就会越严重。
根据以上分析,将人群踩踏风险进一步表述为:
(2)
式中:Ea为场所a内的人群情绪指数,反应人群情绪的异常状态,由专家给定(表征必要条件一);Na为场所a内的总人数,单位人;Sa为场所a有效的人群活动面积,单位m2;Na/Sa为场所a内的滞留的人群平均密度,单位人/m2(表征必要条件二及后果);Nin为场所a入口的人群流动系数,即单位时间内能够通过入口的人数,单位人/(m2·s);Nout为场所a出口的人群流动系数,即单位时间内能够通过出口的人数,单位人/(m2·s);La为场所a内当前人群密度下的人群疏散效率,单位人/(m2·s);(Nin-Nout)/La为场所a内人群密度下的实际净流动系数(表征必要条件三);Ua为场所a内触发因子指数,反应存在人群踩踏事件触发因子的个数,如逆向人群,涡流,激波[19],局部区域人群密度远超阈值等情况(表征必要条件四);Na/La为场所a内当前人群密度下的人群疏散所需时间(表征后果);Ca为后果扩大系数,年龄、性别、生理、心理等因素对人群踩踏事故后果的扩大效应,由专家给定(表征后果)。
(二)人群密度与人群踩踏风险的关系
人群踩踏风险的一个重要因素就是人群密度。这是由于人群密度极大地影响了人的可运动状态,也决定了人群踩踏事故发生后造成的后果严重程度。
Fruin的研究[2]指出,正常情况下,人群的平均移动速度为1.34m/s,但在不同的人群密度下,人群运动速度有不同的等级。

表1 Fruin提出的速度与密度的关系
由此可知,当人群密度小于等于0.5人/m2时,人群能够高速自由移动,而当人群密度大于2人/m2时,所有人的移动速度都受到了限制,只能够低速自由移动。
而另一篇文献反应的人群密度与人群状态的情况如表2所示。[20]

表2 人群密度与人的状态
该研究表明,当人群密度大于5人/m2时,人与人之间距离已经很近,所以仅能够低速跟随他人的移动而移动。
根据文献研究[21]给出的公式,个体所需的最小空间面积取决于个体生理尺寸肩宽Wp和身体厚度Tp,将个体抽象成椭球形得到的空间面积公式为SpE=π/4×WpTp,将个体抽象成长方体时得到的空间面积为SpS=WpTp。
将SpE和SpS取倒数后,得到的则是发生人群踩踏风险的人群密度阈值的最大值ρ。
根据中国人的身体特征,取Wp=0.5m,Tp=0.25m,则SpE=0.098m2,SpS=0.125m2。换算成人群密度阈值为,ρe=10.2人/m2,ρs=8人/ m2。也即当人群密度大于8人/m2时,人群已经无法移动,人与人在空间内互相挤压,稍不留神就会发生人群踩踏事故。
因此综合来看,人群密度与人群踩踏风险关系可以简单归纳为表3所示。

表3 人群密度与人群踩踏风险关系
在不考虑其他因素,只考虑人群密度的情况下,人群踩踏-人群密度风险表达式可以写为
(3)
其中(Na+Nin-Nout)/Sa与人群密度对应,f((Na+Nin-Nout)/Sa)取相应的风险等级值。如(Na+Nin-Nout)/Sa=0.7人/ m2时,Ri=2,即人群踩踏-人群密度风险等级为2。
三、人群踩踏风险与人群到达建模
(一)人群到达
人群到达指的是人群通过区域边界进入公共活动区域或特定区域的情况。人群到达规律反映的是单个人群通过区域边界进入公共活动区域或特定区域的时间间隔分布规律或人数分布规律。
本文依托归元寺春节祭祀活动的案例数据,所界定的人群到达特指香客通过数据采集区域边界进入数据采集区域的情况。这里,用V表示单位时间内人群到达归元寺入口处的期望值。
(二)人群运动
人群运动指的是聚集的人群朝着确定目标或不确定目标的移动过程。
这里的案例数据涉及的人群运动特指香客在数据采集区域的微观人群运动。
(三)基于人群到达的人群踩踏-人群密度风险模型
基于上述分析,可以构建基于人群到达率的人群踩踏风险模型
(4)
当V≤Nin(max)时,人群会按照Nin的速度进入公共场所内,此时人群踩踏风险集中于公共场所内部
(5)
当V>Nin(max)时,人群会集聚在公共场所入口处并形成踩踏风险,此时人群踩踏风险由公共场所入口区域和内部两者的人群踩踏风险共同决定了整体的踩踏风险,且风险等级取较高的那一个。
(6)
式中:Nin(max)为场所a入口的最大人群流动系数,即单位时间内能够通过入口的最大人数,单位人/(m2·s);Nb为入口区域滞留人数;Sb为的入口区域的有效面积。
四、公共场所人群到达规律的统计分析
(一)数据采集
数据采集时间是2016年2月12日(大年初五),对象是武汉市归元寺的春节祭祀活动。
该日,归元寺人流行进方向示意图如图1所示分为两个方向:
一是入寺方向:人群可以从主干道边的三个主要路口前往归元寺,其中钟家村小学侧入口和右侧路口的人流最后汇聚到归元寺正门处。
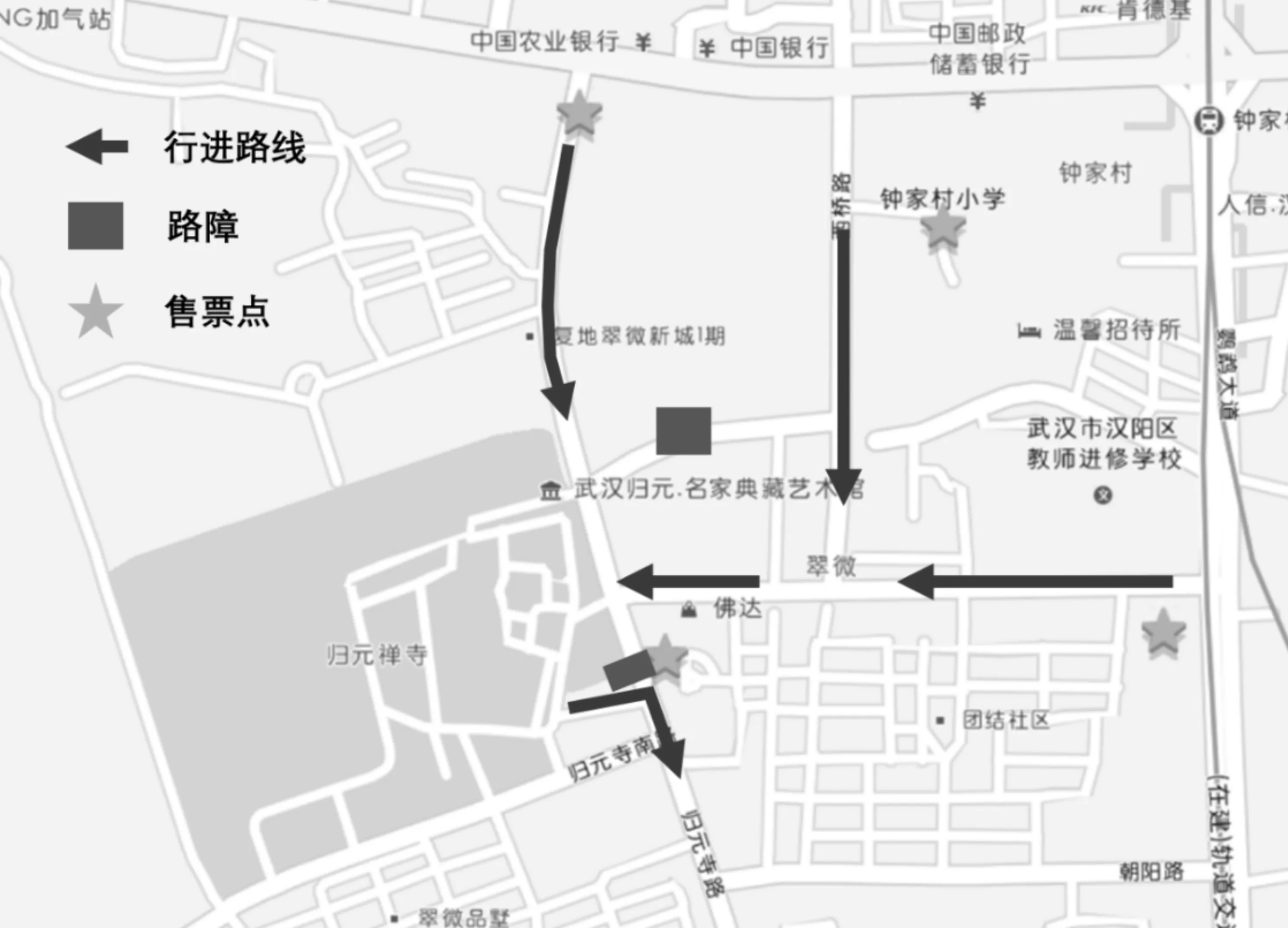
图1 归元寺祭祀进出人流示意图
二是出寺方向:人群从归元寺南路出口处出出口后南行可到主干道附近。
归元寺管理方通过将出入口中间用隔离带分割,控制人流的走向。
视频采集处,即归元寺入口处,归元寺管理方通过隔离带将入口分成了南北两个次入口,南侧(三岔路口侧)的次入口有三条通道,北侧的次入口则有两条通道。由于人流大多汇集于三岔路口侧(占总人数的比约为64%),并且大多从三岔路口侧的次入口进入归元寺,因此本文仅以该侧的入口作为代表来进行研究。隔离带(三岔路口侧)的状况如图2所示。

图2 归元寺入口处隔离带示意图(三叉路口一侧)
隔离带将通道分成了外侧、中侧和内侧三条,内侧的通道最靠近售票口,外侧的通道则离售票口最远。
作者对该入口处的人流进行了视频拍摄,并以这些视频作为研究基础,以5s为采样间隔,在7:50到8:15及10:05到10:20这两个时间段,共采集了40min的人群到达数据。
(二)最短距离效应与入口效应
根据实际数据,对次入口的三个通道进行分别计数后得到表4。
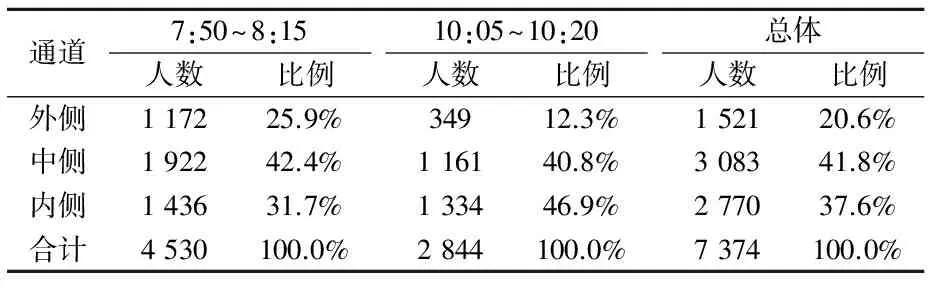
表4 通道人流量统计表
从表4的数据可以看出,中侧通道的人流量最大,平均占比40%以上,外侧通道的人流量最小,最少的时候仅有约12%的人利用该通道。
同时,可以看到7:50-8:15这个时间段,利用外侧通道的人较多,而10:05-10:20这个时间段,利用内侧通道的人则较多。两个时间段的人流量的详细分布如图3、图4所示(由于7:50-8:15分的曲线原图有些模糊不清,故对原始数据进行了15s移动平均,在保证数据趋势特征不变的基础上增加图表的可读性)。由图3可以看出,7:50-8:15这个时间段内,中侧通道的人流量的波动比较稳定,而外侧通道和内侧通道的人流量波动则在14~17分半这个时间段内出现了脉冲式的异常波动。该异常波动表现为外侧通道的人流量突然增多,而内侧通道的人流量骤然减少,如图5所示。
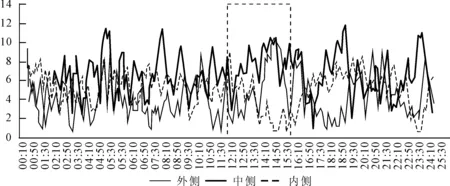
图3 7:50分~8:15分人群到达数(15s移动平均)

图4 10:05分~10:20分人群到达数
由图4可以看出,在10:05-10:20这个时间段内,中侧通道的人流量波动变大,外侧通道在很长一段时间内少有人群同行,而内侧通道的人流量则相对较稳定,如图6所示。
分析通道的设置可知,出现图5和图6的异常情况的原因有两个:其一是离售票处越近的通道越有可能有人进入,其二是越像入口的通道入口越有可能有人进入。
1.离售票处越近的通道越有可能有人进入(最短距离效应)。
由于内侧通道和中侧通道较接近售票处和三叉路口的中心,而大多数人在进入归元寺前都会前往售票处排队买票,或者在三岔路口中间购买黄牛票,之后人会自然走向离自己较进的入口而非远离自己的入口。这种效应如图7所示。
2.越像入口的通道入口越可能有人进入(入口效应)。
由于内中外三条通道均离真正的入口有一段距离,而中侧和外侧特别是中侧的入口很明确地是并排的门状入口,因此通过中侧通道的人流量较稳定。这种效应如图8所示。
最短距离效应和入口效应使得人群偏向于进入特定的通道,造成特定区域中总体人群密度较低但局部密度较高的现象,从而造成人群阻塞、滞留。根据相关学者的研究[22],人群阻塞滞留是引发人群踩踏风险的重要原因之一。
在案例中,这种现象则表现为外侧通道人群较少,且会间断式地形成脉冲式人流。这种脉冲式人流其实是安保人员会间断地引导人群进入外侧通道造成的。

图5 7:50-8:15时间段正常和异常情况对比

图6 10:05-10:20时间段正常和异常情况对比

图7 最短距离效应
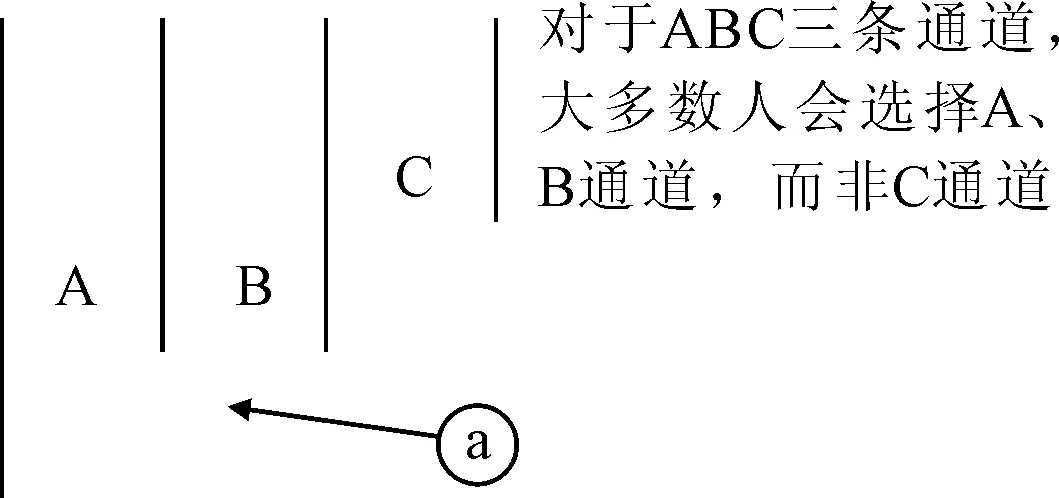
图8 入口效应
五、人群踩踏风险的统计分析
(一)泊松分布检验
一般来说,人群踩踏风险的研究都假定人群的到达服从均匀分布或泊松分布;但并未论证人群到达的统计分布是否服从泊松分布[23]。本文提出运用单个样本的K-S检验来确定样本观测结果是否具有泊松分布的特征。其思路是将人群到达的理论累积频数分布同观测的累积频数分布加以比较,求出它们的最大偏离值,然后参照抽样分布,在给定的显著性水准上(一般为0.05)检验这种偏离值是否是偶然出现的。如果检验统计量大于给定的显著性水平,则说明接受该分布服从泊松分布的原假设,否则拒绝原假设。
将采集到的原始数据导入到SPSS中,使用K-S检验功能后生成如表5所示的结果。
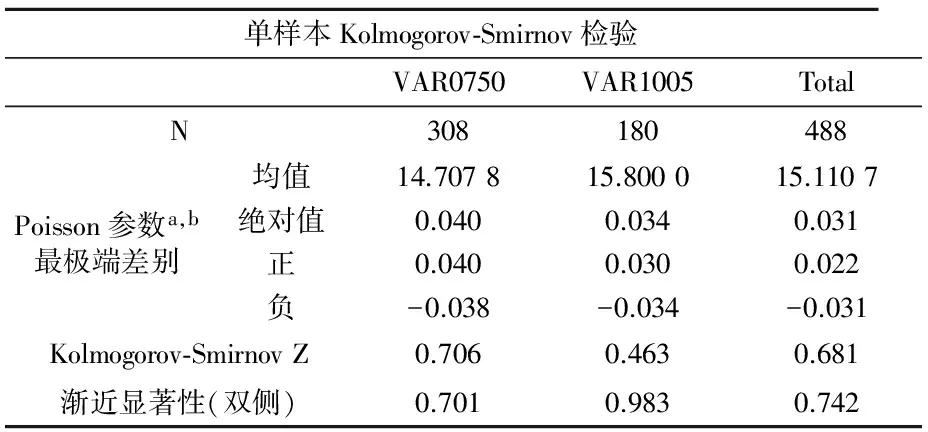
表5 观测数据泊松分布的K-S检验
a.检验分布为Poisson分布
b.根据数据计算得到
表5表明,7点50到8点15时间段采样数据的显著性概率是0.707,10点05到10点20的显著性概率是0.983,数据整体的显著性概率是0.742,不管是分段时间的数据还是总体的数据,双侧检验的显著性概率均大于0.05,因此可以认为人群的到达服从泊松分布。
按照泊松分布的公式,可以在根据实际数据求得相应的λ后,求得泊松分布的概率分布曲线。实际数据整理后可得到图9的人群到达曲线。

图9 综合人群到达-概率曲线图
从图9可以看出,对于整体时间的数据,人群到达的概率曲线与泊松分布的曲线拟合度比较好。说明归元寺春节祭祀活动的人群总体到达服从泊松分布。
(二)人群踩踏-人群密度风险模型案例研究
基于《体育建筑设计规范》及相关体育建筑设计资料设定[24],中国单股人群流量为40~42人/min,本研究单股人群流量取42人/min,即0.7人/s。
参考归元寺的出入口示意图可以发现,归元寺入口处设有三条通道,每条通道都可以同时通过2个人,即可以形成6股单向人流,所以Nin(max)=0.7×6=4.2人/s。
归元寺出口处仅有一个门,可以形成2股人流通道,所以Nout(max)=0.7×2=1.4人/s
依据百度地图的数据,归元寺占地面积约17 500平方米,假设有效活动面积为归元寺占地面积的70%,即12 250平方米,那么Sa=12 250。归元寺入口区域占地面积约为3×50=150平方米,即Sa=150。
由实地观测数据知,大年初五上午8点到10点,归元寺入口处人群平均达到率约为V=3人/s。
将相应数据代入模型,由于V (7) 由于初始的Na=0的情况下,是不会有稳定的人流从出口离开归元寺的,所以这里要假设Na=3×0.5×60×60=5 400,即开园半个小时内只有人群到达并进入归元寺。那么归元寺内部人群踩踏风险等级与开门时间的关系如表6所示。 表6 人群踩踏风险和开门时间关系 由于归元寺正月初五的开放时间为早上6点到晚上6点,一共12个小时,因此归元寺内的人群踩踏风险等级也最多会到达等级4。但如果要把人群踩踏风险控制在等级3及以下,则应该控制开园约10小时,也就是下午4点开始停止检票入园,此时人群踩踏-人群密度风险等级仅为等级3 另外,按照模型计算,到约9点15分时,归元寺内部的人群数目为(3-1.4)×2.75×60×60+5 400=21 240人,人群密度为20 240÷12 250=1.73人/m2,此时归元寺内部的人群踩踏-人群密度风险等级为2级。 而按照9点15分时的实际数据(如图10所示) 图10 2016年2月12日9点15分归元寺客流量情况 9点15分,寺内在场人数为12 755人,寺内人群密度为12 755÷12 250=1.04人/m2,人群踩踏-人群密度风险等级也同为2级。 不过按照模型计算,当日9点15分的客流累计人数应为3×3.25×60×60=35 100人,这与实际客流累计人数相差约2万人。这说明初五归元寺的祭祀活动6点到8点那段时间人群到达并不服从平均到达率为3人/s的泊松分布,而更有可能是开始人极多,随后迅速衰减的幂次分布。所以当时在入口区域的人群踩踏-人群密度风险可能会很高。 根据本文研究发现的人群到达规律和人群密度风险模型,公共活动的管理者可以从以下几个方面来提高人群踩踏风险的管理。 (一)事前合理规划活动规模 基于公共活动人群到达并服从泊松分布这一结论,管理者可以根据以往活动的人流量数据和当前的服务水平确定相应参数,将参数输入计算机模拟程序后了解人群滞留过程和阈值等数据。根据这些模拟结果,管理者可以通过控制售票数量,控制进入区域的人数等方式控制活动的人群踩踏风险。 (二)事前合理规划人群通道 人群通道的合理设置可以有效引导人流移动方向,防止人群聚集和阻塞,从而降低人群踩踏风险。基于入口效应和最短距离效应,人群通道的规划要考虑到通道进入处的形状和分布,以期达到真正的分流作用。以归元寺为例,如图11所示,将内中外三条通道的入口处均设置成门状,理论上将提高外侧通道的利用率。 图11 归元寺入口处隔离带改进的建议方案 (三)事中合理控制人群密度 基于人群踩踏-人群密度风险模型,在活动进行时,管理者要及时根据当前的人流量评估活动场所内的人群踩踏风险等级。在人群踩踏风险等级提高时,及时对人群进行有效引导,避免整体或局部人群密度过大。在人群踩踏风险等级可能突破管理预期时,要及时限制人流,对人群进行有效的疏散,避免造成人群踩踏风险事故。 (四)事中实时发布区域人群踩踏风险指数 虽然人群聚集与分散具有一定的随机性,但个体却会有意识地避开觉得有风险的人群密集区域。因此实时发布区域人群踩踏风险指数,引导人群流动方向,能够有效地避免局部区域的人群密度过大,防止人群踩踏风险等级继续升高。 [1]Hankin B D W R A. Passenger Flow in Subways[J]. Journal of the Operational Research Society,1958,9(2):81-88. [2]Fruin J. Pedestrian planning and design[C]. Metropolitan Association of Urban Designers & Environmental Planners,1971. [3]Pauls J. The movement of people in buildings and design solutions for means of egress[J]. Fire Technology,1984,20(1):27-47. [4]Thompson P A, Marchant E W. A computer model for the evacuation of large building populations[J]. Fire Safety Journal,1995,24(2):131-148. [5]Fang Z, Lo S M, Lu J A. On the relationship between crowd density and movement velocity[J]. Fire Safety Journal,2003,38(3):271-283. [6]张培红,鲁 韬,陈宝智,等.时间压力下人员流动状态的观测和分析[J].人类工效学,2005,11(1):8-10,17. [7]吕 雷,程远平,王 婕,等.对学校教学楼疏散人数及疏散速度的调查研究[J].安全,2006(1):10-13. [8]胡玉婷.复杂场景密集人群的流动规律研究[D].上海:上海交通大学,2014:20-25. [9]Lee R S, Hughes R L. Exploring Trampling and Crushing in a Crowd[J]. Journal of Transportation Engineering, 2005,131(8):575-582. [10]Lighthill M J W G B. On Kinematic Waves. I. Flood Movement in Long Rivers[J]. Proceedings of the Royal Society of London A Mathematical Physical & Engineering Sciences, 1955,229(1178):281-316. [11]Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic[J]. Nature, 2000,407(6803):487-490. [12]K T. Microscopic Pedestrian Flow Characteristics: Development of an Image Processing Data Collection and Simulation Model[D].Sendai:Tohoku University Japan, 2002:11-30. [13]宋卫国,于彦飞,范维澄,等.一种考虑摩擦与排斥的人员疏散元胞自动机模型[J].中国科学E辑:工程科学材料科学,2005(7): 725-736. [14]张青松,刘金兰,赵国敏.人群拥挤踩踏事故后果微观建模及模拟分析[J].安全与环境学报,2008(4):164-168. [15]孙 立,赵林度.基于群集动力学模型的密集场所人群疏散问题研究[J].安全与环境学报,2007(5):124-127. [16]刘 茂,王 振.行人和疏散动力学研究现状及进展[J].安全与环境学报,2006(S1):121-125. [17]王 振.城市公共场所人群聚集风险理论及应用研究[D].天津:南开大学,2007:20-25. [18]王起全.基于赋权关联度算法的地铁拥挤踩踏事故风险研究[J].中国安全科学学报, 2013(5): 94-100. [19]卢春霞.人群流动的波动性分析[J].中国安全科学学报,2006(2):30-34. [20]任常兴,吴宗之,刘 茂.城市公共场所人群拥挤踩踏事故分析[J].中国安全科学学报,2005(12):102-106. [21]冉丽君,刘 茂.人群密度对人群拥挤事故的影响[J].安全与环境学报,2007,7(4):135-138. [22]王艳.地铁踩踏事故机制分析及应对措施探讨[D].北京:北京交通大学,2015:20-25. [23]胡明伟.交叉口车辆到达统计分布的实证研究[J].道路交通与安全,2009(2):10-15. [24]张青松.人群拥挤踩踏事故风险理论及其在体育赛场中的应用[D].天津:南开大学,2007:20-25. (责任编辑 王婷婷) Stampede Risk in Public Place Based on the Crowd Arrival Pattern CAO Qing, XIE Ke-fan (SchoolofManagement,WUT,Wuhan430070,Hubei,China) Public activities can enrich people’s life, but sometimes the crowd stampede occurs. Once the crowd stampede occurs, the consequences can be very serious. Therefore, monitoring, early warning and pre-control of the crowd stampede risk have aroused more and more attention of organizations and government of the public activities. By analyzing the data of the Guiyuan Buddhist Temple in the Spring Festival in 2016, on the basis of the Poisson distribution and the microscopic scale, this paper demonstrates the crowd arrival of public places and finds that crowd arrival has two patterns, which are the entrance effect and shortest distance effect. The parameters can be used in the computer simulation of crowd stampede risk analysis. And the conclusion of this paper can be a reference to the optimization of stampede predetermined plan and design of public activities to enhance the ability to crowd control and reducing the population stampede risk. crowd stampede; stampede risk; crowd density; crowd arrival; Poisson Distribution 2016-12-20 曹 青(1991-),男,湖北省武汉市人,武汉理工大学管理学院硕士生,主要从事风险管理研究; 谢科范(1963-),男,湖南省益阳市人,武汉理工大学管理学院教授,博士生导师,博士,主要从事风险与应急管理研究。 国家社会科学基金重点项目研究成果(15AGL021) X928.03 A 10.3963/j.issn.1671-6477.2017.04.0001

六、公共场所人群踩踏风险的防控建议

