中国全要素农田水利效率的地区差异和门槛效应研究

宋 敏 汪 琦 吉晓雨

(河海大学商学院,江苏南京 211100)

中国全要素农田水利效率的地区差异和门槛效应研究

宋 敏 汪 琦 吉晓雨

(河海大学商学院,江苏南京 211100)

农田水利作为我国农业基础设施投资的重要组成部分,对农业经济增长及农民增收具有重要影响。基于DEA在全要素生产的框架,构建全面衡量我国农田水利效率的指标--全要素农田水利效率,选取2001—2015年省级面板数据,运用DEA-Malmquist方法测算31个省的全要素农田水利效率,并对不同区域农田水利效率进行对比分析。研究结果表明我国全要素农田水利效率存在明显地区差异,东北地区效率最高、超过农业大省聚集的华东和华中地区;全要素农田水利效率与区域经济发展水平存在不完全匹配现象,主要与农田水利效率及影响因素之间的非线性关系有关。基于农田水利效率省际差异,采用门槛回归模型检验影响全要素农田水利效率的门槛特征,研究结果显示：农村经济发展水平对农田水利全要素生产率存在显著的收敛门槛效应、机械动力投入对农田水利全要素生产率存在明显的加速门槛效应。

农田水利;全要素生产率;门槛效应;DEA-Malmquist

农田水利建设作为国家基础设施建设的重要组成部分,对促进农村经济发展、增加农民收入、减少贫富差距具有重要作用。我国对于农田水利的重视程度越来越高, 2011年,水利部落实了中央一号文件,明确到2015年全国水利投资总额将达1.8万亿元,农田水利建设资金将占20%;“十二五”期间,我国农田水利建设投资额达4 264亿元;2016年,水利部办公厅印发《2016年农讯水利工程要点》,提出要完善“十三五”农村水利专项规划,出台《深化农田水利改革的指导意见》,大规模推进农村水利建设。随着农田水利受到重视,农田水利效率问题也成为不可避免的焦点,各地区由于自然条件、资源禀赋以及经济发展水平不同,全要素农田水利效率也存在较大差异。基于此,笔者从农田水利全要素生产率角度进行分析,探索我国农田水利效率的区域差异,并对其影响因素进行门槛特征分析。

一、 相关研究回顾

近年来,国内外学者对农田水利的相关理论和一些问题做了大量研究,取得了较大成果。大多数研究主要集中在农田水利建设与农业增长关系上,普遍认为农田水利投资与农业经济增长之间具有显著正向关系,但是地区之间存在一定的差异。袁怀宇通过建立农业经济增长模型进行回归分析表明,农田有效灌溉面积和水土流失治理面积增加能够显著促进农村经济增长[1];郭唐兵等利用2001—2010年中国省级面板数据实证分析了农田水利发展与农业增长的关系,研究表明农田水利发展对农业增长的影响存在区域差异[2]。袁汝华等通过构建C-D函数测算水利科技进步对国民经济发展的贡献率,结果表明在资本和劳动力投入趋于稳定的状态下,水科技进步对水利经济发展的贡献越来越大[3]。郭珍等研究了水利投资的减灾效果,结果表明：增强水利投资能够有效地降低旱灾成灾率、水灾成灾率,特别是旱灾成灾率,保证农民收入[4]。

学者对于农田水利效率的研究主要以农田水利投资效率的测算和评价为主,Rosegrant等通过对比农田水利投资与农村科研、农村道路投资对比得出农田水利投资额高但是效率低的结论[5];俞雅乖运用数据包络模型分析区域农田水利财政支出效率,通过回归分析发现农田水利财政支出效率存在显著的地区差异,东部和中部地区对农田水利的管理水平高于西部地区,而西部和中部地区的规模报酬高于东部地区[6];叶文辉等分别从纵向和横向两个方面分析云南省近几年水利投入产出效率,发现农田水利投资效率低下、部分州市处于无效状态,得出云南省农田水利效率普遍低下的结论[7];汤洁娟通过对1960—2014年我国东部、中部、西部地区相关统计数据的分析发现,西部地区农田水利工程的社会经济效率增长率位居国内最高水平,中部地区其次,而东部地区相对最低,这与地区经济和产业结构变动有关[8];刘石成通过对2011年我国13个粮食主产区的农田水利基础设施投资效率的研究表明,各地农田水利基础设施投资效率具有较大的空间差异性,吉林、辽宁、四川、江西4个地区属于DEA有效,包括规模有效和技术有效,其他9个地区属于非DEA有效且技术效率和规模效率呈现不均衡发展,规模效率呈现递增和递减两种种状态[9]。

纵观已有文献,大多数研究集中于农田水利基础设施与农业经济增长的关系以及投资主体、投资对象以及管理模式的研究,对农田水利效率的研究富有成效,但有些问题有待深入探讨,因此笔者在已有研究基础上,针对全要素农田水利效率以及影响农田水利效率的因素进行深入分析。以往研究主要从投入产出的角度衡量农田水利效率,并未从全要素生产率角度进行测算,基于2001—2015年我国31个省的面板数据,运用DEA-Malmquist指数法测算全要素生产率视角下的农田水利效率,用该指标作为衡量农田水利效率的指标,便于从技术进步角度评价我国农田水利效率。研究发现,农田水利效率存在较大的空间差异,在此基础上进一步通过门槛面板估计方法,实证检验影响全要素农田水利效率的门槛效应。

二、全要素农田水利效率差异分析

1.模型选择

数据包络分析法(DEA)是由美国学者运筹学家Charnes等提出的一种评价多种投入、多种产出的综合效率测算模型,由于此法无需考虑输入输出指标的单位量纲问题,可以规避参数法的多种限制,因此是目前比较有效的测算农田水利投资效率的方法。根据规模报酬是否可变的假设,DEA可以分为规模报酬不变模型(CCR)和规模报酬可变(BCC)模型。笔者采用BCC模型对农田水利效率进行评价。

(1)

式中:x0,y0表示被评价单位的投入量和产出量;λ表示组合系数;θ代表了效率评价指数,θ=1时表示有效率,θ<1时表示效率较低;s+,s-表示松弛变量。

(2)

该指数反映在t期技术条件下,从t～t+1期的农田水利全要素生产率的变化率,同理在t+1期技术条件下,从t～t+1期全要素生产率变化的Malmquist生产率指数:

(3)

选取两者几何平均值代替生产率变化:

Mt(xt+1,yt+1,xt,yt)=

EFF(xt+1,yt+1,xt,yt)·TEC(xt+1,yt+1,xt,yt)

(4)

式中EFF表示规模效率变化指数;TEC表示技术进步指数,指标大于1表示技术进步、等于1表示无进步、小于1表示技术退步。因此,衡量农田水利效率的全要素生产率被拆分成两部分:一部分是规模效率,一部分是技术进步指数变化。

2.变量选取与说明

此次数据全部为面板数据,研究对象是全要素农田水利效率,选取31个省份(直辖市、自治区)作为决策单元,研究不包括香港、澳门、台湾地区。鉴于评价农田水利效率的多方面性以及存在的效益外溢,因此在研究其效率时综合考虑经济效益、社会效益和生态效益。具体测算指标为农田水利全要素生产率,该指标能够更加直观反映我国农田水利投资效益,同时对农田水利全要素生产率进一步分解便于为提高农田水利效率提供方向性建议。具体投入产出指标见表1。数据来源于2001—2015年《中国农村统计年鉴》《中国统计年鉴》《中国水利统计年鉴》以及各省份的历年统计年鉴。对于个别统计数据的缺失,笔者采用移动平均法进行补充。

考虑对效率问题进行实证研究时投入项和产出项之间需要符合“同向性”假设,即随着投入项的增加,产出项不得减少,所以在测算之前,先用Pearson相关性检验法对指标进行检验,结果显示变量均在1%显著水平下通过双尾检验,符合要求的同向性原则。

表1 主要变量及定义

数据来源:作者整理所得

3.实证分析及结果

(1)基于时间视角的农田水利投资效率分析

对农田水利全要素生产率测算使用的是基于投入产出的Malmquist指数法,假设规模报酬可变(VRS),使用DEAP2.1软件。

图1是2002—2015年我国农田水利全要素生产率变动及分解情况。总体上看,我国农田水利全要素生产率指数呈现上升趋势,2002—2005年农田水利全要素生产率指数基本保持在1左右,变化幅度较小,农田水利效率比较稳定。通过效率分解看,这一时期农田水利效率主要来自于规模效率的提升,技术进步的贡献较小,主要原因是该时间段农田水利主要依靠劳动力要素投入,农田水利相关技术较落后,尚未转化成实际的产出效益。2006—2010年,农田水利全要素生产率指数出现下降趋势,主要原因是“十一五”期间我国发生较大自然灾害,比如长时间的低温雨雪冰冻、地震、泥石流等对我国有效灌溉面积、农林牧渔总产值均产生较大的影响,因此“十一五”期间我国农田水利全要素生产率指数呈现降低的趋势。2009年以后,随着我国农田水利效率呈现先平稳后加速增长的状态,特别是2013年以后,农田水利全要素生产率指数呈现大幅增长的态势,主要是我国逐渐意识到农田水利基础实施是国家基础设施的短板,对农田水利投资不断加大、对农田水利重视程度越来越高。此外,农田水利建设作为一种准公共产品,其投资和收益之间的建设周期较长,收益的实现存在一定时滞性,在前期投资落地之后要经历一段转化时期才能够转化为收益。从农田水利全要素分解可以看出,该时期全要素农田水利效率指数的增长主要来自于技术进步的贡献,规模效率作用较弱,技术进步对农田水利效率的促进作用显著高于规模效率。

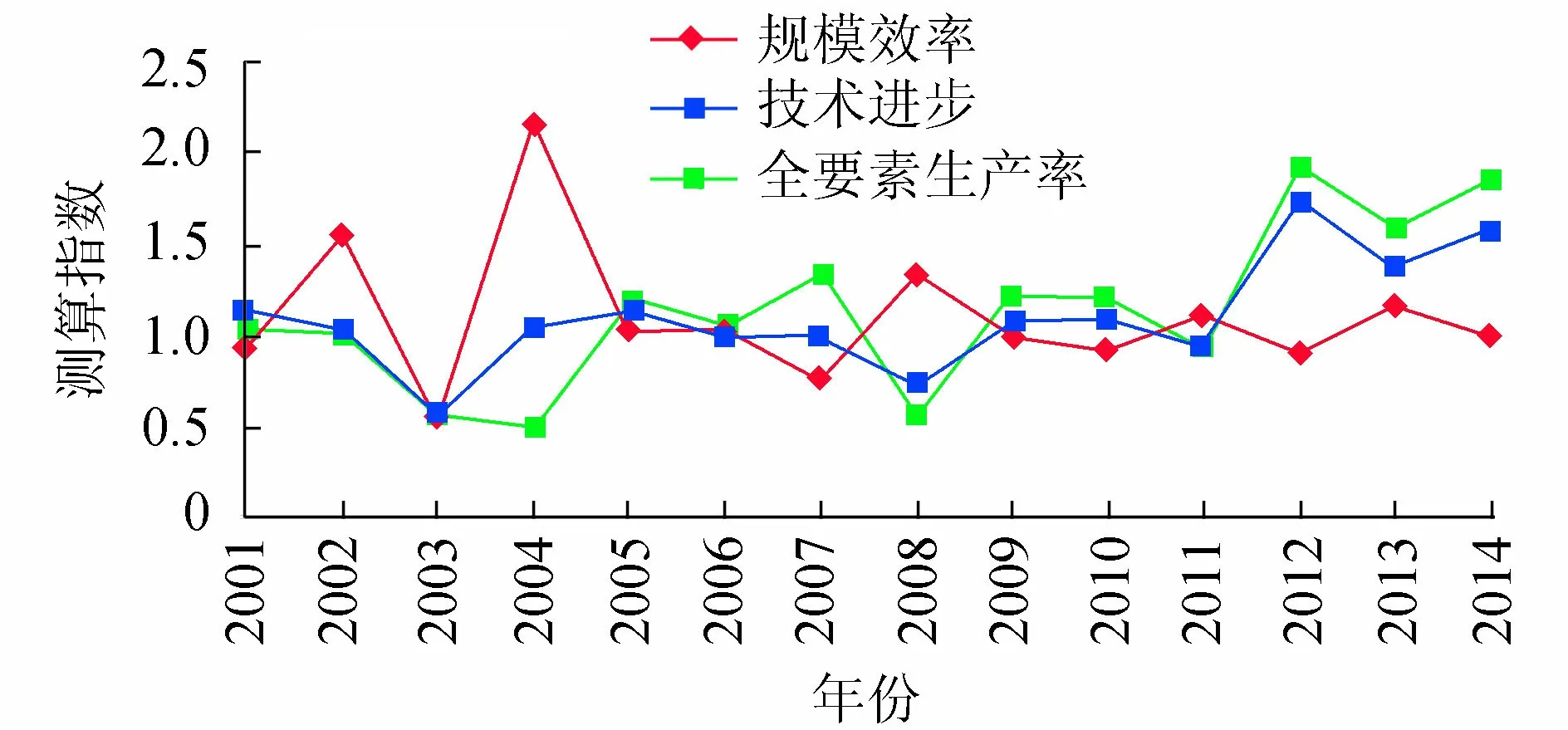
图1 2002—2014年我国农田水利全要素生产率及其分解

(2)基于空间视角的农田水利效率分析

图2 2001—2015年我国7个区域农田水利投资效率DEA测算结果

为横向对比我国各区域农田水利效率的情况,运用DEAP2.1对我国31个省、市、自治区的农田水利效率进行测算(图2)。从图2可看出,我国7个区域的农田水利效率处于严重不均的状态,其中整个东北地区的效率最高、几乎接近于1表示完全有效,同时其效率的波动较小、具有稳定性,说明对于该地区的农田水利效率较高。主要是因为东北地区是我国主要的优质粮食主产区,对农田水利基础设施的建设十分重视;同时东北地区幅员辽阔,具有广阔的松嫩平原、三江平原和黑河地区能够进行机械化农业生产,作为我国的粮食主产区和老工业基地,黑龙江的农田水利发展方法科学、体系完善、设备配套,能够产生很高效率。而传统农业大省聚集区域的华中和华东,其农田水利基础设施的投资效率并不高,整体效率水平偏低,特别是华中地区。这主要是由于华中和华东地区水资源条件良好,人们无需建造和维护更多的农田水利基础设施就可以满足农业生产的基本需要,从而缺乏对于农田水利投资充分利用的动力。农田水利效率最低的是西南地区,整体仅仅为0.7,远低于全国平均水平,很大原因是虽然我国西南地区整体自然资源丰裕,但受自然条件约束较大,多山地并不适合机械化大生产,“靠天吃饭”的状况没有改变,比如2010年西南多个省区持续遭遇大旱困扰,农作物大面积绝收;其次就是由于西南地区经济发展水平相对落后,用于农田水利建设的投资相比于其他地区较为匮乏,农田水利建设存在较大的问题。

为更深入分析我国各区域农田水利全要素生产率的差异,选取2014和2015年各地区的数据进行Malmquist指数分解分析(表2)。从各区域农田水利全要素生产率分解状况可以看出,我国各区域农田水利全要素生产率存在差异的主要原因是各区域技术进步贡献不同,技术进步对全要素生产率指数具有更显著影响,其中技术进步指数较高的地区为东北、华东以及华南地区,相应地,这些区域的农田水利效率明显高于其他区域。

从研究结果可以看出,农田水利效率存在明显的地区差异,东北地区效率值最高,超过了经济发展水平较高的华东地区和传统农业大省聚集的华中地区。考虑农田水利效率的地区差异性,初步猜测农田水利效率存在非线性变化的特征,为此进一步运用非线性的门槛回归模型对这一问题做深入研究。

三、全要素农田水利效率的“门槛效应”分析

1.门槛回归模型

由Hanse提出的非动态面板门槛模型,将门槛值作为一个未知变量纳入实证模型中,构建解释变量回归系数的分段函数,然后对所得门槛值及门槛效应进行一系列估计和显著性检验。Hansen提出的门槛模型将“内生分组”代替了“外生分组”的武断性,将样本划分为不同的组别,有效避免了主观判断带来的误差,从而能够更好地揭示不同分组解释变量与被解释变量之间的变化关系。模型的基本形式如下:

表2 我国31个地区2014年全要素生产率及其分解情况

(5)

(6)

式中被解释变量xi是一个m维列向量;qi为“门槛变量”,可以是解释变量xi中的一个回归元,也可以作为一个独立的门槛变量。引入虚拟变量将式(5)(6)合并:

yi=θ1′xi+δ′xid(r)(qi>r)+ei

(7)

yit=α0+xitβ1I(qit≤γ)+xitβ2I(qit≥γ)+εit

(8)

式中i=1,2…n,表示不同地区;t=1,2…T表示时间;yit为被解释变量,具体表示各地区农田水利效率(TFP);xit为被解释变量,qit为门槛变量,分别表示农村经济发展水利和机械投入水平;γ为待估计未知门槛值,门槛值确定后其他参数值也能相应的确定;I为指示函数,相应条件成立取1,否则取0。

为了防止设定误差的存在,需要对门槛效应的存在性进行检验,沿用Hansen提出的似然比检验。不存在门槛效应的原假设为H0:β1=β2,备择假设为H1:β1≠β2,在H0的假设下,公式(8)的形式如下:

yit=α+β0x1it+β1x2it-μi+νit,μi>0

(9)

式(9)不包括门槛参数γ,因此参数γ在零假设下没有定义,传统的检验统计量不满足标准分布,Hansen建议使用Bootstrap来模拟似然比(LR)检验统计量的非标准性分布,获取近似分布的临界值,从而得到基于似然比的P值,P值足够小拒绝原假设,存在显著门槛效应。统计量LR表达式为:

(10)

式中S0表示在原假设H0下的残差平方和,渐进自助P值的方程式为:

(11)

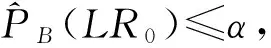
2.变量选取与数据说明

本研究沿用资本投资Invi,t、人力资本投入Labi,t、机械投入Techi,t、水资源丰裕程度E作为变量,另外选取农户人均收入的对数值LNACI作为经济发展水平的替代指标,一方面我国十八大报告提出:“要实现到2020年城乡居民人均收入比2010年翻一番的目标”;另一方面,农户人均收入作为衡量人民生活、农村人口的实际经济水平的重要指标,能够比总体的农村经济指标更好反映农村经济发展的实际情况。

3.实证分析及结果

门槛回归模型研究首先需要确定门槛数量并对门槛进行估计,笔者分别在单一门槛、双门槛和三门槛的假设下进行估计,同时计算F统计量,并借助Bootstrap方法重复抽样500次得到P值。采用农村经济发展水平和机械投入水平作为门槛变量进行门槛效应检验,回归结果为表3。

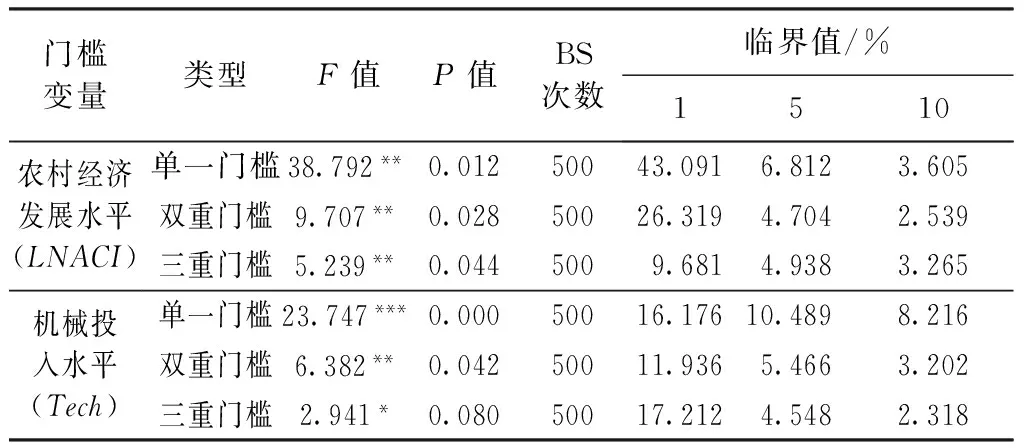
表3 门槛效果自抽样检验

注:*、**、***分别代表在10%、5%、1%显著水平上显著

(1)农村经济发展水平

在确定门槛效应存在且确定门槛个数之后,需要对门槛值水平进行测算并确定门槛值的置信区间。采用优化搜索的方法确定门槛值,将农村经济发展水平作为门槛变量时的门槛值以及置信区间(表4)。

表4 农村经济发展水平作为门槛值的门槛估计值和置信区间

表4可以看出,当为单一门槛检验时,门槛估计值为1.11,在95%的置信区间,两个门槛区间值也是非常接近。图3的似然比函数图清晰展示了门槛值及置信区间的构造过程:横轴表示门槛参数,纵轴表示似然比函数值,虚线表示95%置信区间上的似然比临界值,置信区间则是由小于临界值的似然值构成,其中最小值为门槛值。而当双重门槛时,由于第2个门槛值1.955的置信区间较大,因而影响了其准确性,因此进一步证实笔者只选取农村经济发展水平的单一门槛的合理性和科学性。

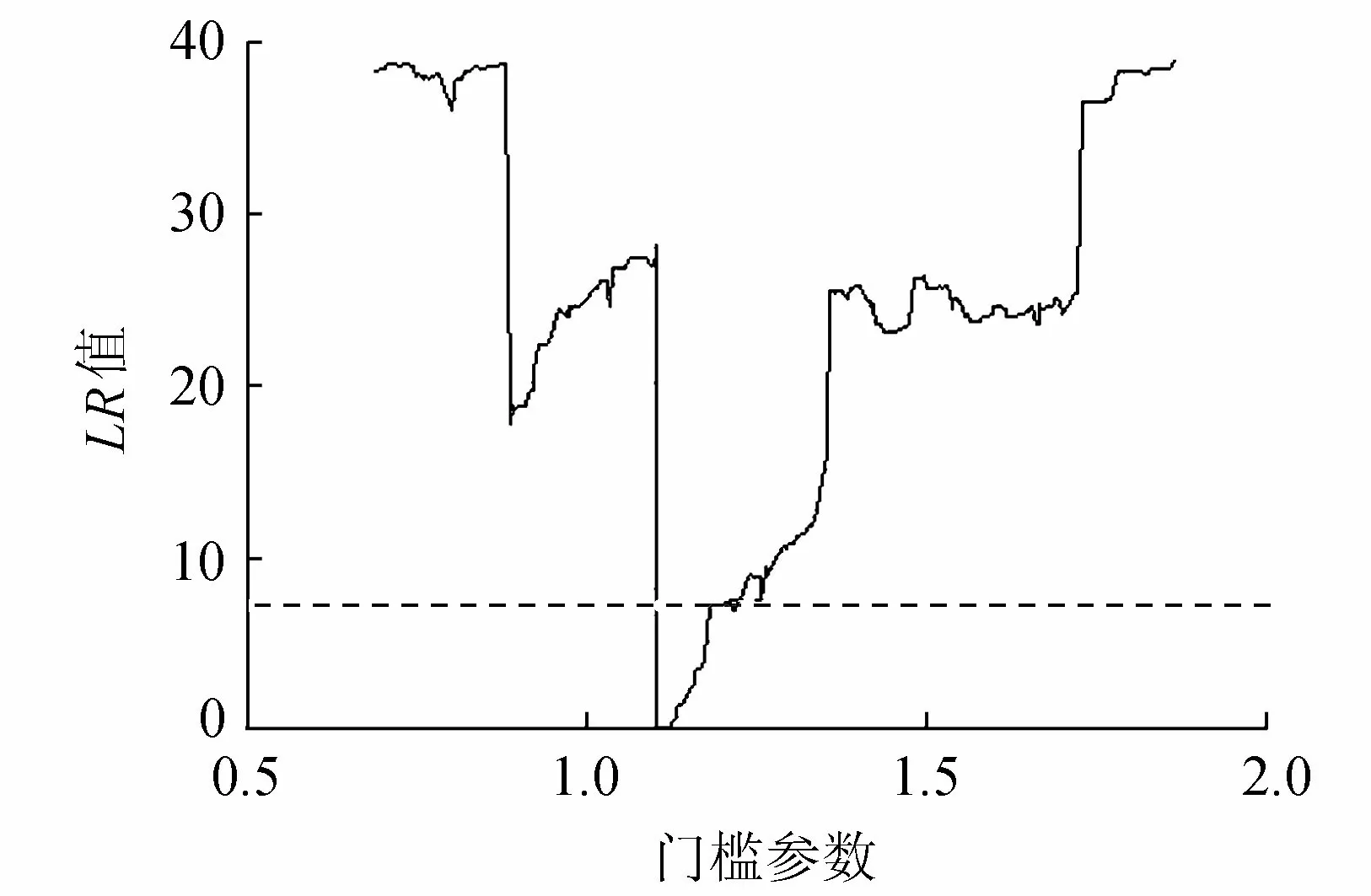
图3 农村经济发展水平为门槛值效果图

在对门槛效应存在性和门槛值进行确定后,使用农村经济发展水平的单一门槛来进行回归分析(表5)。从表5可以看出,当农村经济发展水平作为门槛变量时,随着经济发展水平的不断提高及农村整体生产水平的提升,农村经济发展水平对农田水利全要素生产率有较大的促进作用,其影响系数达到了1.44。然而随着农村经济水平不断提高,农村经济发展水平对农田水利效率的显著促进作用有所减弱。当LNACI跨过1.1的门槛值之后,促进作用下降到了0.037,很好解释了我国从“十五”到“十二五”期间农田水利效率出现了降低的趋势,然而这并不意味着当我国跨入经济发展门槛之后,就要减少农田水利投资,该阶段农田水利效率的生产函数正在发生相应的变化,仅仅通过维持或提高投资程度是无法促进效率提高的。

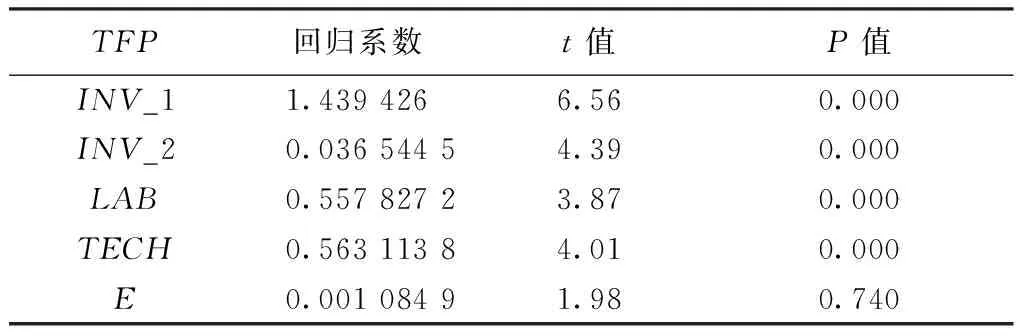
表5 农村经济发展水平为单一门槛的面板门槛模型估计结果

(2)机械投入水平

当机械投入水平作为门槛变量时,采用同样方法确定门槛值水平以及门槛水平的置信区间(表6),相应的似然比函数图为图4。可以看出机械水平作为单一门槛效应非常显著。

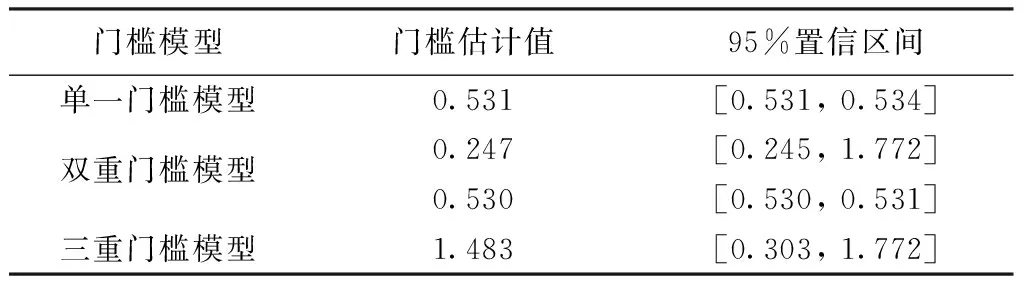
表6 机械投入水平为门槛值的门槛估计值和置信区间

图4 机械投入水平为门槛值效果图

在确定机械投入水平对农田水利投资存在门槛效应,同时证明为单一门槛效应之后,本使用单一门槛模型进行回归分析(表7)。

表7 机械动力投入为单一门槛的面板门槛模型估计结果

由表7可知,在机械动力投入的不同区间所得的估计系数在5%的显著性水平下均为正,表明机械动力的投入与农田水利效率存在正相关关系。这一结论解释了随着经济发展以及社会生产力的提高,我国在机械动力投入不断提高所带来的总体农田水利效率增长的长期趋势。随着机械动力投入的不断提高,相应的估计系数由0.039上升至0.982,说明在门槛值划定的两个区间内,机械动力投入对农田水利效率的影响程度存在显著的差异,在越过门槛值之后机械动力投入对农田水利效率的增长效应显著增强,由于我国东北地区工业化程度较高,农用机械投入明显高于其他地区,农田水利效率是最高的一个区域,与实证结论相吻合。

四、 结论与建议

应用2001—2015年我国31个省的面板数据测算农田水利的全要素生产率,同时进行分区域的对比分析,结果表明我国农田水利效率存在显著的地区差异:东北地区效率最高,几乎接近于1的完全有效状态;传统农业大省聚集区域的华中地区和华东地区,全要素农田水利效率并不高;最低的是西南地区,整体接近0.7的水平,远低于全国平均水平。

为进一步分析我国农田水利这种区域差异,运用门槛回归模型对影响农田水利效率的因素进行研究,在分别将农村经济发展水平以及机械动力投入作为门槛分析变量时,两者回归结果均显著:①当引入农村经济发展水平作为门槛变量时,结果表明其对全要素农田水利效率存在门槛效应,在门槛值之前,农村经济发展水平对农田水利效率存在显著的促进作用,但是达到1.1的门槛值之后农村经济发展水平对农田水利效率的影响显著减少,系数值的大小仅为0.037,这一结论很好解释了为什么经济发展水平较高的华中和华东地区农田水利全要素生产率却低于东北地区。②农用机械动力对农田水利全要素生产率存在显著的加速门槛,在越过门槛值之后,农用机械动力的投入对农田水利效率的影响系数明显增强,由0.039上升至0.982,主要原因是农用机械动力的大量投入会产生规模效应,推动农田水利效率的提高。

对于经济发展水平较为落后的地区,重点应缩小本地区与其他地区的经济发展水平的差异,扩大农田水利效率提高所需的资本投入和劳动力投入;对于经济发展水平较高同时越过门槛的地区来说,主要是改善农田水利技术投入、增加机械动力投入实现农田水利全要素生产率的提高,同时重视资源的合理配置,积极为农田水利投资决策提供科学的指导意见和约束政策,保证农田水利投入与其他投入的协调、维持各地区农田水利投资的平衡,使得盲目的农田水利投资得到遏制或消除。

[1] 袁怀宇. 农田水利建设与农业经济增长关系实证研究[J].广东农业科学,2013, 40(25): 122-126.

[2] 郭唐兵,叶文辉. 我国农田水利运营效率的实证研究:基于2003—2010年省级面板数据的DEA-TOBIT两阶段法[J].山西财经大学学报, 2014,36(2):63-71.

[3] 袁汝华,孔德财,吴凤平,等.水利科技进步投入产出作用机理及贡献率测算:来自江苏省的实证分析[J].河海大学学报(哲学社会科学版),2013,15 (4):50-53.

[4] 郭珍,曾福生. 水利投资减灾效果评估:基于中国省际面板数据的实证研究[J].河海大学学报(哲学社会科学版), 2014,16 (3):49-54.

[5] ROSEGRANT M W,EVENSON R E.Agricultural productivity and sources of growth in south Asia[J].American Journal of Agricultural Economics, 1992,74(3):757-761.

[6] 俞雅乖.我国农田水利财政支出效率的省级差异分析[J].农业经济问题, 2013(4):55-63.

[7] 叶文辉,孙莉莉,姚永秀. 农田水利供给的有效性分析:以云南省为例[J].经济问题, 2015, 27(9):73-80.

[8] 汤洁娟.农田水利工程效率及其影响因素分析:基于DEA-Tobit模型多阶段实证[J].求索, 2014(6):85-89.

[9] 刘石成. 我国农田水利设施建设中存在的问题及对策研究[J]. 宏观经济研究, 2011(8):40-44.

(责任编辑：高 虹)

10.3876/j.issn.1671-4970.2017.04.008

2016-06-05

教育部人文社会科学规划基金项目(15YJA790052); 国家自然科学基金面上项目 (41471456)

宋敏(1975—),女,四川眉山人,副教授,从事水利经济研究。

F32

A

1671-4970(2017)04-0040-07