ARIMA模型在石油价格预测分析中的应用
2017-09-03周宇
周宇
(湖南现代物流职业技术学院,长沙410131)
ARIMA模型在石油价格预测分析中的应用
周宇
(湖南现代物流职业技术学院,长沙410131)
原油即石油,是人类生产生活不可或缺的重要能源之一,其价格受到众多因素的影响,其中既包括定量因素,也包括定性因素,要找出众多原因并准确预测石油价格是十分困难的。本文通过利用SAS统计软件,对石油价格的时间序列进行单位根、白噪声等检验,建立ARIMA模型并预测分析,最后根据建立的模型以及预测结果做出结论。
ARIMA模型;石油价格;预测
一、研究方法与理论基础
ARIMA模型全称为差分自回归移动平均模型,是由博克思(Box)和詹金斯(Jenkins)于20世纪70年代初提出的著名时间序列预测方法,所以又称为box-jenkins模型。ARIMA模型公式可简记为:。在ARIMA(p,d,q)模型中,既包含p阶自回归系数多项式φ(B),也包含了q阶移动平均系数多项式Θ(B),而且还有把时间序列成为平稳时所做的差分次数d。如果一时间序列是不平稳的,那就不能够直接建立ARMA模型。但是通过恰当阶数的差分以后,该不平稳序列就可变为平稳,从而能对差分后得到的序列进行ARMA拟合分析。在此原理下,现实中许多经济变量虽然不具平稳性,但也能够通过建立ARIMA模型得到较好的分析预测。
二、实证分析
(一)数据的选取
本文以比较具代表性的WTI原油价格为例,选取2008年4月至2013年3月周数据,共261个样本数据,进行模型拟合。数据来源于美国能源情报署(http://tonto.eia.gov/)发布的每周数据。
(二)ARIMA模型的建立
1.时间序列的观察
在拟合模型之前需要先判断石油价格序列是否平稳。要是该序列已经平稳,则可直接建立ARMA模型。要是序列不平稳,则需进行差分。通过描绘时间序列图,观察时间序列图是否有趋势性或者周期性,便可大致判断时间序列是否平稳。
利用SAS统计软件编译程序并运行后,可得石油价格时间序列图。从图中可观察到,虽然石油价格并没有显示明显的周期性,但是自2009年一月,石油价格大致上呈现出上升趋势,从总体上看,并不能认为石油价格的统计特性不随时间的平移而变化。因此从图形的初步识别可认为该序列非平稳。
2.平稳化处理
由于石油价格序列非平稳,难以用已知的信息把握其随机性,故对石油价格进行一阶差分,得到石油价格差分后的时间序列图。差分后的序列没有明显的趋势性或周期,基本上可视为平稳序列。除了通过观察时间序列图以外,还可以通过观察自相关系数图判断时间序列的平稳性。自相关系数很快地衰减至在两倍标准差范围以内,故自相关图也说明了该序列是平稳的。为稳妥起见,除了用图形识别以外,还需做进一步的识别判断。
3.单位根检验
时间序列图和自相关图都是以图形对序列平稳性作直观判断,这种判断并不精确。判断序列的平稳性需要更加精确的方法。此处用单位根检验法判断时间序列是否平稳。结果显示,零均值、单均值、有趋势的单位根检验P值均小于0.0001,在显著性水平为0.05的水平下,该序列是平稳的。
4.白噪声检验
建立ARIMA模型除了要求差分后的序列平稳以外,还要求该序列非白噪声。白噪声性也称为纯随机性,一个序列为白噪声序列,代表着该序列的变动是随机的、没有规律的,序列值之间没有任何相关性,序列的过去并不影响它未来的发展。此时序列将没有分析的价值,也无需建立模型对它进行分析。所以,分析研究的序列必须是非白噪声序列。下表1为白噪声检验结果。
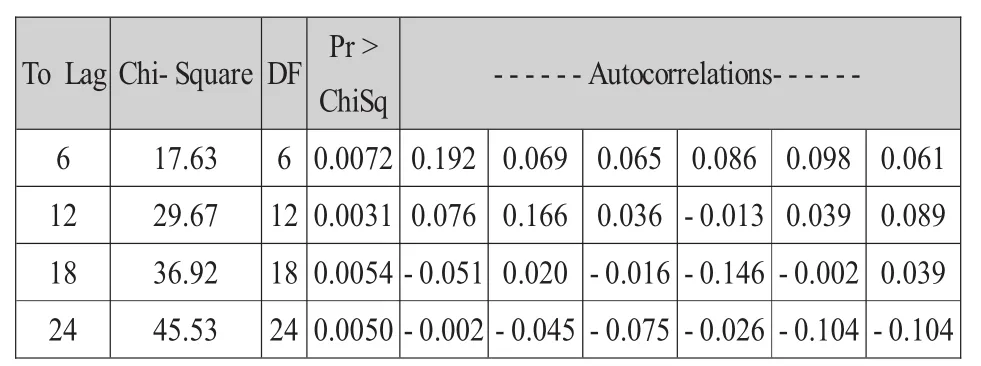
表1 白噪声检验结果
平稳序列通常具有短期相关性,而长期延迟的序列值之间相关性较弱,故可检验延迟6期和延迟12期来判断序列是否为白噪声序列。在石油价格差分后的序列的检验结果中,延迟6期和延迟12期的P值小于0.05,故认为该序列属于非白噪声序列,即序列值之间存在相关关系,可对该序列进行建模分析。
5.模型识别与定阶
根据自相关系数与偏自相关系数的拖尾或者截尾可分别确定ARIMA(p,d,q)模型中的q和p。
由样本自相关图可看出,q可选择1或者2,根据样本偏自相关图,p可选0或者1。除了用样本自相关图和样本偏自相关图作粗略的判断外,还须用更精确的判断准则——BIC准则为模型定阶。BIC准则全称贝叶斯信息准则,由AIC准则即最小信息量准则发展而来。根据BIC准则,能使BIC函数达到最小的模型就是最优模型。与其他模型相比,当p=1,q=0时,BIC值最小,因而建立ARIMA(1,1,0)模型是最合适的。
6.建立ARIMA模型
一是模型拟合。设为石油价格,为石油价格的一阶差分,用SAS输出结果如图1。

即拟合得到的ARIMA模型为:

或可记作:xt=1.19302xt-1-0.19302xt-2+εt
模型中参数的t值为3.16,P值小于0.05,故模型的参数显著。
二是模型检验。拟合模型后需要检验残差序列是否还有未提取的信息,即检验残差序列是否纯随机序列,以此评价模型的拟合优度。图1中残差序列各滞后阶的P值均远大于0.05,表明残差序列为白噪声序列,残差序列基本上没有值得提取的信息,故该模型提取的信息量已经足够,模型的拟合效果好。
7.模型的预测
利用2008年4月至2016年5月石油价格的周数据建立的ARIMA(1,1,0)模型可预测2016年4月及5月上半旬每周的石油价格。
图2石油价格的拟合效果图显示出该模型的拟合与实际值较为符合,该模型拟合效果好。但石油价格的预测值与实际值相比有一定的偏差,预测的4期中误差百分比在1.68%-10.00%范围内波动。在前两期的预测中,误差百分比较小,尤其是第一期的预测值跟实际值相差很近,该预测是比较准确的。但是第三期的误差百分比就已达10%,随着预测期数的加大,模型的预测误差将越来越大,同等水平下的置信区间将逐渐变大,这也是利用ARIMA模型预测的缺陷。单从预测结果看,石油预测价格的波动幅度不大,略有上升趋势,而就目前国际上石油的整体形势而言,此预测结果是比较准确的。
三、结论

图2 石油价格变动区间图
ARIMA模型假定事物的发展符合渐进的特征,过去的行为影响着当前和未来,而其他的影响因素对于过去、现在及将来的作用是不变或者变化较小,故可基于历史数据和确定趋势预测未来。ARIMA模型只需采取现有数据便可建模,与其他建立多因素的回归模型相比,无需考虑变量之间的协整关系以及多重共线性等问题,而且精度也比较高。在时间序列的发展模式方面,ARIMA模型不需要先验信息,在一定程度上放宽建模的要求,可通过反复识别修改获得理想的模型。但是,在序列预测方面,ARIMA模型只能较准确地对短期进行预测,预测区间变大,则模型预测误差也会增大,那么较远期预测的结果就没有很大的意义。当然,ARIMA模型也需要根据实际情况的变化,引入新的数据序列进行调整更换,这样才会使ARIMA模型的预测效果变得更好。
影响石油价格的因素十分复杂,本文抛开其他因素的影响,仅采取历史数据拟合模型,拟合出来的模型会有一定的误差。根据本文建立的石油价格ARIMA模型,预期短期内石油价格将稳中有升。而日前科威特石油大臣哈尼·侯赛因表示近期国际石油价格可能将略有下滑。由于2016年世界石油消费增长不多,西方国家经济形势不太稳定等等原因,都将可能导致国际石油价格的下跌。国际形势方面,伊朗是石油大国,其经济很大一部分靠石油出口支撑,而其石油却遭欧盟“禁运”,欧盟有可能另寻石油进口导致油价上涨。令人担忧的国际局势对国际石油价格的变动将有着复杂的影响。本文对于石油价格的预测分析仅仅是短期的,要对石油市场进行远期的判断还需更加深入的研究。对于石油价格的预测,建议除了用模型拟合分析以外,还需结合当前环境、时局的变化做合理的判断,预测结果才能更接近实际。
[1]丁静之,阂 骥,林 怡.ARIMA模型在石油价格预测中的应用[J].物流技术,2008(7).
[2]季 静.时间序列模型在石油价格预测中的应用研究[D].长春:长春工业大学,2012(9).
[3]肖龙阶,仲伟俊.基于ARIMA模型的我国石油价格预测分析[J].南京航空航天大学学报,2009(10).
[4] 任鑫恚.科威特石油大臣预测油价将下跌[N].中国统计出版社,2013-04-14.
[5]王 超.美欧禁运伊朗石油收入减半[N].汇能资讯,2013-05-27.
[责任编辑:谭志远]
F476.22
A
1005-913X(2017)08-0023-02
2017-05-17
周 宇(1982-),女,辽宁营口人,讲师,高级统计师,硕士,研究方向:计量经济学。
