增压器涡轮箱热-结构强度分析及试验验证

龙鑫， 陈少林， 靳鹏， 刘朝峰， 刘艳东， 张涛

(湖南天雁机械有限责任公司技术中心， 湖南 衡阳 421005)

增压器涡轮箱热-结构强度分析及试验验证

龙鑫， 陈少林， 靳鹏， 刘朝峰， 刘艳东， 张涛

(湖南天雁机械有限责任公司技术中心， 湖南 衡阳 421005)

为了能够直接验证热-结构耦合仿真计算的精确性，以某型增压器涡轮箱为研究对象, 运用CFD分析软件与FEA分析软件同步耦合仿真计算涡轮端温度场，然后将求解得到的温度场节点温度赋给结构分析模型，再求解涡轮箱模型的热应力。在发动机台架上运行增压器，发动机运行时采用与增压器CFD仿真计算相同的边界参数，采用红外热像仪测定考察区域的温度场分布，通过非接触式应变测量系统测定考察区域的应变分布，提取考察区域标记考察点的温度及应变结果，并与仿真计算的温度及应变结果进行对比分析，结果表明，采用热-结构耦合分析方法求解的涡轮箱温度和应变精度能满足工程设计要求。

涡轮箱； 温度场； 应变； 结构强度； 仿真

增压器是一种压缩新鲜空气进入气缸提升发动机动力的装置。研究涡轮箱的温度场分布和应力分布情况可以有效预测涡轮箱的热-机械疲劳寿命，降低涡轮箱开裂的风险，提高涡轮箱的耐久可靠性。涡轮箱失效最主要的方式是热应力，其次是蠕变和氧化，因此研究涡轮箱热应力是当前涡轮箱设计研究的重要工作。近几年来国内外科技工作者致力于热应力方面的研究[1-4]，热-机械应力分析理论及热-机械疲劳理论都得到了长足的进步，其中疲劳分析理论Sehitoglu方法已运用到工程实践中[5-7]。霍尼韦尔公司(Honeywell)、美国材料与试验协会(ASTM)及其他科研人员对增压器涡轮箱热-机械疲劳方面进行了深入的研究[8-16]。

1 涡轮端分析模型的建立

增压器涡轮端模型包括流体模型与固体模型，其中固体模型分为热分析模型与结构分析模型，包括涡轮箱、涡轮、放气阀门、简化的排气歧管及排气管、预紧螺丝等，流体模型包括涡轮端流道、涡轮、放气阀门等组成的封闭腔体。

1.1 涡轮端分析模型的离散

涡轮端流体模型(见图1)总体上可分为旋转域与静止域，局部可以分为一个旋转域和一个固定域。旋转域命名为Rot_Fluid，旋转域的边界层初始值为0.01 mm，共设置10层，增长率为1.2，旋转域网格数为2 103 642个。静止域流道入口段，命名为Housing_Fluid，边界层初始值为0.02 mm，共设置10层，增长率为1.3，静止域网格数为836 587个。

由图2可见，涡轮端的模型组件由简化的排气歧管、涡轮箱、涡轮转子、放气阀门、简化的排气管组成，该模型全部采用二阶四面体单元。

图1 CFD仿真计算模型

图2 涡轮端有限元离散模型

图3中标记的1～8号点为数据处理使用的考察点，在增压器相同位置有相应的标记测点。

图3 涡轮箱离散模型考察点位置

1.2 载荷边界条件

流体计算边界条件包括进出口边界、旋转域转速、壁面边界条件等。发动机工况为3 500 r/min(0.5% FS)、全负荷，增压器涡前温度(涡轮箱入口温度)为924 ℃(温度超过600 ℃时，误差为±1 ℃)，涡前压力(涡轮箱入口压力)为59.8 kPa(0.5% FS)，涡后温度(涡轮箱出口温度)为834 ℃，涡后压力(涡轮箱出口压力)为16.2 kPa(0.5% FS)，涡轮转速为(180 000±500) r/min。分析模型采用k-omega，SST湍流模型。将初始条件设为出口边界，初始化后进行求解。

涡轮端的边界则需要与实际工况相结合。增压器安装在发动机上运行时受到冷却风机的强制冷却(冷却区域见图4)，为了得到较好的计算结果，对强制冷却区域进行了划分，不同冷却区域的对流传热系数与层膜温度不尽相同。

图4 标定转速工况示功图

2 计算结果及分析

2.1 流体计算结果及分析

20世纪80年代以后，随着改革开放以及社会经济的发展。闽南语合唱作品更趋多元化，在保留部分原汁原味的“乡土”色彩外也开始融入一些情感与唱腔，使得合唱歌曲更贴近生活气息。如:无伴奏女声合唱领唱《雨来檐头流》(泉州作曲家杨双智)，同声三部闽南语合唱《十二月果子歌》(台湾作曲家刘晏良创作)等作品。至今，这些作品仍然流传于海峡两岸，影响甚广。

从温度分布来看，涡轮端气体膨胀做功，温度逐步降低。截取流道YZ平面(涡轮径向)的切面作为考察对象，由图5可见，流道进口温度高，沿着流道到涡轮轮毂方向，温度逐渐降低；旋转域的温度分布呈外部高内部低的规律。整个涡轮流道切面温度最高为922 ℃，在流道入口处，温度最低为543 ℃，在轮毂表面附近。截取流道ZX平面的切面(涡轮轴向)作为考察对象, 由图6可见，涡轮流道入口侧的温度高于流道出口侧的温度；放气阀门孔附近的温度高于其他位置处的温度，这是由于在该工况下，放气阀门处于开启状态。由图7和图8可见，压力分布基本与温度分布一致，在放气阀门孔处有局部压力突变。

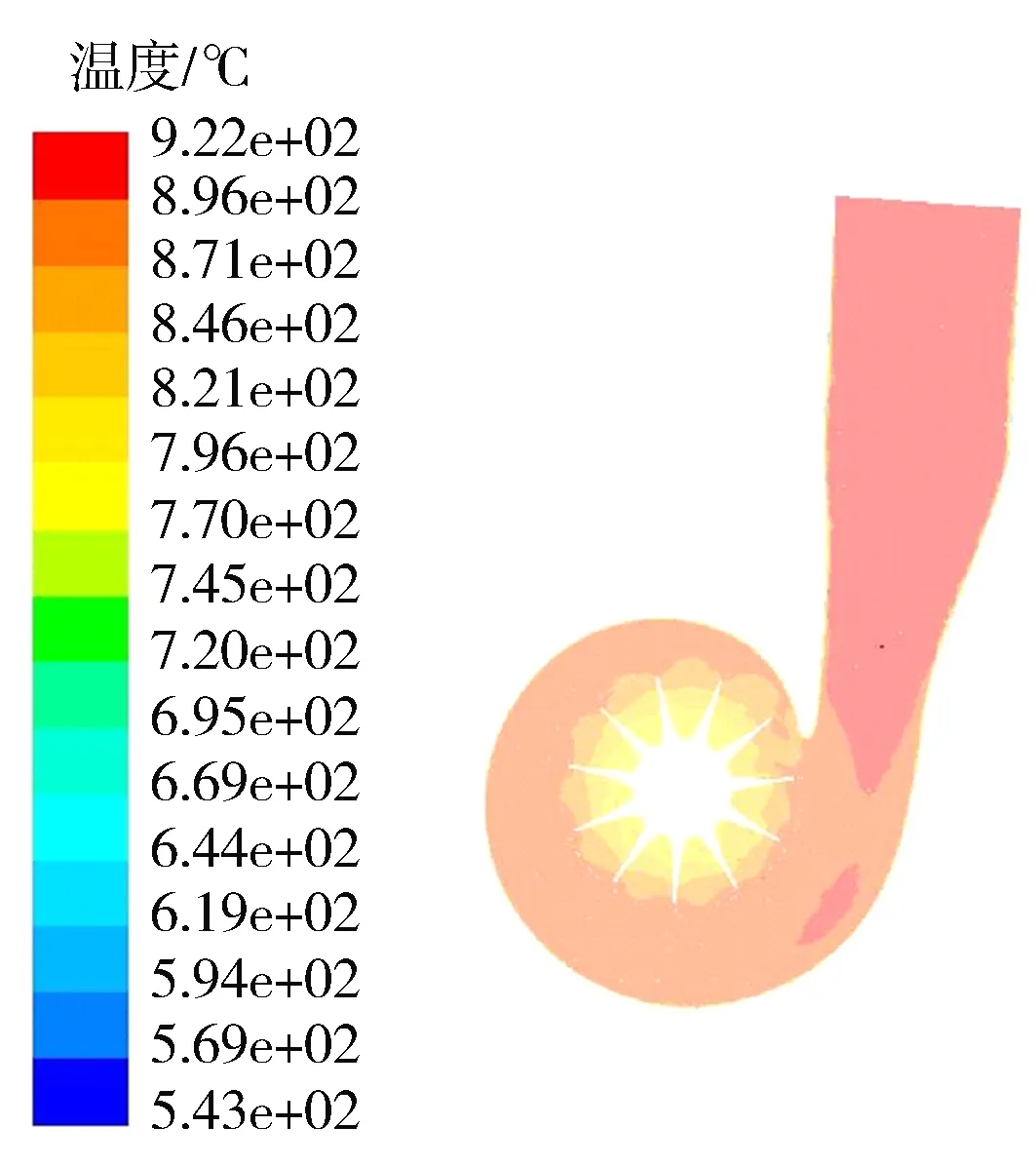
图5 流道YZ平面温度分布

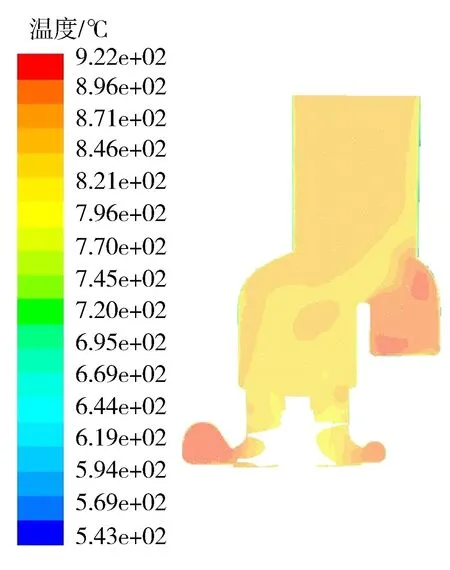
图6 流道ZX平面温度分布

图7 流道YZ平面压力分布

图8 流道ZX平面压力分布

2.2 固体模型温度场计算结果及分析

由图9可见，涡轮端组件的最高温度为880 ℃，在涡轮箱喉口位置处；放气阀门处温度也比较高，但是阀门轴与轴套温度梯度较大，这也是造成轴套变形的重要影响因素之一。从涡轮的温度分布来看，流体进入部位的温度高，流体流出部位温度低，这与涡轮实际温度分布规律一致，说明温度结果具有一定正确性。

图9 涡轮端温度分布

涡轮箱温度分布见图10。涡轮箱最高温度为830 ℃，在放气阀门孔与涡轮出口中间的隔板上，这是由于放气阀门开启后，高温排气直接从放气阀门孔流出作用在该隔板上，造成较高的温度。

图10 涡轮箱温度分布

2.3 结构计算结果及分析

涡轮箱热应力分布见图11。最大热应力在外壁面的出口法兰下方，该处结构有局部突变，内壁隔板温度高，造成该处温度梯度高，热应力大。由于涡轮箱各个位置的温度分布不均匀，单独考察应力不能很好地预测疲劳裂纹的位置，而通过涡轮箱累积塑性应变值更能直观地发现涡轮箱的风险位置。由图12可见，喉口、隔板边缘倒角处、流道外壁面倒角位置、隔板与涡轮箱壁面交接的外壁面累积塑性应变均较大，这些位置均可能是涡轮箱裂纹的风险位置。

图11 涡轮箱等效应力分布

图12 涡轮箱累积塑形应变分布

总应变包括弹性应变、非线性应变、热应变等，非线性应变包括塑性应变、蠕变应变。由图13至图16可见：涡轮箱的总应变最大值为2.94×10-2；热应变为1.92×10-2，在总应变中占据较大比例；弹性应变相对总应变来说数值较小，弹性应变值为2.1×10-3；在局部出现塑性应变和蠕变位置的非线性应变较大，非线性应变值为1.38×10-2，大多数位置的非线性应变为0。

图13 涡轮箱温度总应变

图14 涡轮箱弹性应变

图15 涡轮箱非线性应变

图16 涡轮箱热应变

3 试验及数据对比分析

进行了温度和应变的试验测试以验证仿真的准确性。试验中分别采用Vic-3D/2D非接触应变测量系统和红外热像仪测量应变和温度。Vic-3D/2D非接触应变测量系统采用最佳化的3D数字图像相关性运算法则，为机械试验提供三维/二维空间内全视野的形貌、位移及应变数据测量。由于此系统运用白光散斑相关性技术，因此物体的真实位移可以被测量,并且可获得物体表面的每一点上的拉格朗日应变张量。

3.1 温度场试验及应变测量

涡轮箱实体考察点的位置与图3标记的考察点位置相同。Vic-3D使用DIC(数字图像相关)技术，因此，在测量之前需在待测物表面制作斑点。制作好的实体模型考察点和散斑见图17。

首先安装红外热像仪，然后安装非接触式应变测量相机，在捕捉影像之前只需进行影像对焦及光圈调整、表面斑点处理及3D校正。调校好非接触式应变测量相机后，需进行相应的标定工作。在增压器未运行情况下，用指定的温度标定板加热至高于室温，通过标定板与待标定物的温度差来标定红外热像仪。对于应变测量相机的标定，需要将拍得的形变过程影像储存起来，过后重新载入软件作形变的分析处理。如果待测物本身已具有足够的斑点，则不需再做额外的斑点处理。

图17 涡轮箱标记线和散斑图

3.2 试验结果及仿真计算结果对比分析

由表1可见，1～4,7～8测点温度测试值与仿真计算值误差均小于5%，在误差允许范围内。5，6测点的误差大于5%，这是由于在5，6测点的正前方有一台冷却风机对增压器进行强制冷却。冷却风机的冷却过程是一个强制对流传热过程，本次仿真计算没有将该冷却域加入计算，仅采用经验的对流传热边界不能完全模拟该冷却的真实过程，因此造成温度计算结果与测试结果误差较大。

表1 温度计算结果与测试结果对比分析

由表2可见，1，2，4，7测点的总应变误差均小于5%，测试值与仿真计算值在误差允许范围内。由于5、6测点仿真计算的温度结果与测试结果误差较大(见表1)，导致仿真计算的热应变误差较大，而热应变占总应变的较大比例，因此，5，6测点总应变的仿真计算结果与测量结果的误差较大。3，8测点的误差大于5%，原因是被测涡轮箱的区域是一个球面，应变测量相机捕捉微小变形时会造成一定的误差，同时还有发动机台架振动、高温使散斑效果变差等因素，累积误差均会增大。总之，造成误差的可能原因包括：1)温度测量值与仿真计算值有一定的误差；2)应变测量仅能测定面应变；3)发动机振动较大，测量误差较大；4)数据处理及散斑等原因造成；5)测量边界的误差。

表2 应变计算结果与测试结果对比分析

4 结论

a) 在温度对比研究中，温度场试验结果与仿真计算结果总体分布一致，散斑质量差的位置温度误差大；

b) 在应变对比研究中，由于热应变占据总应变的比重大，因此，温度误差大的位置热应变误差大；

c) 在试验过程中采用冷却风机对增压器进行强制冷却，而在仿真计算中没有计算该冷却域，该位置温度的测量值和计算值误差较大。

[1]ZienkiewiczOC,MorganK.Finiteelementsandapproximation[M].Swansea:PineridgePress,1983:324-325.

[2]BatheKJ.FiniteElementproceduresinengineeringanalysis[M].Englewood:Prentice-Hall,1982:143-144.

[3]Shiang-WoeiChyuan.Finiteelementsimulationofatwin-cam16-valvecylinderstructure[J].FiniteElementsinAnalysisandDesign,2000,35(7):199-212.

[4] 廖日东，左正兴,邹文胜.对高速大功率柴油机用气缸盖机械负荷有限元分析边界条件施加方式的探讨[J].兵工学报,2001,21(1)：5-10.

[5]XumingSu,MichaelZubeck,JohnLasecki,etal.Thermo-mechanicalfatigueanalysisofcastaluminiumenginecomponents[J].FiniteElementsinAnalysisandFatigue,2003,30(4):159-173.

[6]NeuRW,HuseyinSehitoglu.Thermo-mechanicalfati-gue,oxidation,creep:PartⅠ.DamageMechanisms[J].MetallurgicalTransactionsA,1989,20:1755-1767.

[7]NeuRW,HuseyinSehitoglu.Thermo-mechanicalfati-gue,oxidation,creep:PartⅡ.LifePrediction[J].MetallurgicalTransactionsA,1989,20:1769-1781.

[8]MichaelJVerrilli,MichaelGCastelli.Thermo-mechanicalfatiguebehaviorofmaterials:secondvolume[C].[S.l.]:ASTM,1994:27-41.

[9]AVL.Turbochargertestrigbriefintroductionintothesystem[M].Graz:AVLListGmbH,2005:1-4.

[10]JohnBHeywood.Internalcombustionenginefundamentals[M].NewYork:McGraw-Hill,1988.

[11]FaridAHDAD,CarolCAI.FiniteElementanalysisofturbinehousing[J].HoneywellTurboTechnologies,2007:7-16.

[12]MichalVajdak.Thermalstressanalysisofturbinehousing[J].HoneywellTurboTechnologies,2006:06-0854.

[13]MickaelCormerais,PascalChesse,Jean-FrancoisHetet.Turbochargerheattransfermodelingundersteadyandtransientconditions[J].Int.J.ofThermodynamics,2009,12(4):193-202.

[14]LicuDN,FindlayMJ,GartshoreIS,etal.Transientheattransfermeasurementsusingasinglewide-bandliquidcrystaltest[J].JournalofTurbomachinery,2000,122:546-552.

[15]FaridAhdad,RagupathyKannusamy,DamodharanB.AnalyticalapproachofTMFpredictionforcomplexloading[C]//AsmeTurboExpo:PowerforLand,Sea,&Air.[S.l.]:ASTM,2010:581-590.

[16]Sun-puiNg,RogerNg,WinnieYu.Bilinearapproximationofanisotropicstress-strainpropertiesofwovenfabrics[J].ResearchJournalofTextile&Apparel,2005,9(4):50-56.

[编辑： 姜晓博]

Thermo-Mechanical Strength Analysis and Experimental Validation for Turbine Housing of Turbocharger

LONG Xin, CHEN Shaolin, JIN Peng, LIU Chaofeng, LIU Yandong， ZHANG Tao

(Technology Center, Hunan Tyen Machinery Co., Ltd., Hengyang 421005, China)

In order to verify the accuracy of thermal structural coupling simulation analysis, a certain type of turbine housing of turbocharger was taken as the research object. The synchronous coupling simulation and calculation of turbine end temperature field was conducted by using CFD and FEA software, the gained joint temperature of temperature field was input to structural analysis model and the thermal stress of turbine housing model was solved. With the same boundary parameters as simulation, the turbocharger ran on the engine test bench and the temperature field and strain distributions of inspection area were measured by using the thermal infrared imager and non-contact strain measurement system respectively. The temperature and stain results were acquired and compared with simulation results. The results show that the temperature and strain accuracy of turbine housing can meet engineering design requirements.

turbine housing; temperature field; strain; structural strength; simulation

2017-01-14；

2017-04-11

龙鑫(1983—)，男，工程师，主要研究方向为汽车车用涡轮增压器；hntylx@163.com。

10.3969/j.issn.1001-2222.2017.04.011

TK423.5

B

1001-2222(2017)04-0053-06