基于欠定盲源分离的柴油机曲轴轴承故障诊断方法研究

朱江涛

(山西交通职业技术学院， 山西 太原 030031)

基于欠定盲源分离的柴油机曲轴轴承故障诊断方法研究

朱江涛

(山西交通职业技术学院， 山西 太原 030031)

针对柴油机曲轴轴承振动信号盲源分离的欠定问题，提出了基于相空间重构和动态聚类奇异值分解的适定化方法。首先通过引入广义时间窗的概念确定最佳时间延迟和嵌入维数，重构信号相空间矩阵；然后对其进行奇异值分解，并对奇异值进行动态聚类以确定最佳重构阶数，进而重构得到虚拟观测信号，从而将欠定问题转变为适定或超定；最后利用自适应Parafac方法对原观测信号与虚拟观测信号构成虚拟传播路径进行盲源分离得到有效源信号。仿真结果表明，该方法可有效分离出混合信号中的源信号，并将其应用到柴油机曲轴轴承故障诊断中，诊断准确率提高了18.4%。

振动信号； 欠定盲源分离； 相空间重构； 奇异值分解； 动态聚类； 故障诊断

由于柴油机振源众多，在对柴油机轴承故障进行诊断时，反映轴承故障的振动信号常被淹没在其他振动信号之中，导致检测的信号信噪比较低，严重影响柴油机故障诊断的可靠性和准确性[1]。近年来盲源分离技术迅速发展起来，为从混合信号中提取轴承故障特征信息提供了新思路。在柴油机振动信号盲源分离中，往往假设观测信号的数目不小于源信号的数目。而在实际应用中，由于传感器安装不便或源信号受干扰严重，观测信号数目会少于原信号，此时需要在欠定状态下对混合信号进行分离。对于欠定盲源分离，已有的研究主要是基于源信号的稀疏表示，借助聚类算法实现[2]。但是，由于柴油机轴承振动信号是多个振源信号以未知的形式混叠而成的复杂信号，因此，对于柴油机振动信号，源信号的稀疏性假设并不一定成立[3]。

针对上述问题，提出了基于欠定盲源分离的柴油机轴承故障诊断方法。利用相空间重构和奇异值分解构造虚拟观测信号，从而将盲源分离从欠定转变为适定或超定，进而采用自适应Parafac方法将轴承故障特征信息从混合信号中分离出来，并将其应用到柴油机轴承故障诊断中，提高了故障诊断准确率。

1 基于广义嵌入窗长的相空间重构

1.1 相空间重构原理

x(i)，i=1,2，…N为单变量时间序列，对其进行相空间重构，得到嵌入维数为p、时间延迟为τ的吸引子轨迹矩阵[4]：

(1)

式中：q=N-(p-1)·τ，且p>q。

为得到合适的嵌入维数p，F.Takens提出在假设数据不受噪声影响且无限长的条件下，只要嵌入维数p≥2u+1，其中u为原动力系统吸引子维数，则重构轨迹构成的系统与原动力系统拓扑等价。此为延迟嵌入定理[5]，后来T.Sauer等把该定理推广到了存在噪声的情形。

1.2 嵌入维数与时间延迟的确定

在相空间重构中，嵌入维数p与时间延迟τ的选取非常重要，其精度直接影响着相空间重构后描述奇异吸引子特征不变量的准确度。大量实验证明，p和τ的选取并不是相互独立的，而是有着较强的关联[6]。为建立时间延迟与嵌入维数的关联，引入广义嵌入窗长的定义[7]。

假设能够从给定的观测量中确定一个合适的延迟Γ，得到的重构相空间从整体上反映了原系统特性。那么，对于嵌入维数为p的相空间矢量，能够计算出重构相空间中任意两个元素的时间延迟与Γ差值的和[7]：

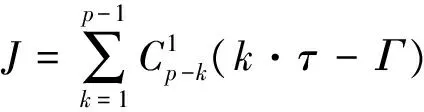
(2)

因此，当J=0时所选择的τ能够使重构相空间任意两个元素时间延迟的平均值为适当的Γ，即

(3)

由式(3)可以得出：

(4)

式中：p为嵌入维数；τ为时间延迟。此时的延迟Γ为广义嵌入窗长，对于任意的观测量，广义嵌入窗长是一个确定的值，对于式(4)中的3个变量，只要知道其中的2个变量，就可以求得另一个变量[6]。

定义r(Γ)为

(5)

r(Γ)反映了观测量之间的非关联程度，因此，当c(Γ)=r(Γ)时的Γ为最佳的广义嵌入窗长，将r(Γ)代入式(5)得到c(Γ)=0.707 ，此时的Γ即为所求。

为求得时间延迟τ，引入时间延迟的自动算法，该算法利用平均位移计算最佳的时间延迟，克服了自相关函数法的不足。将式(1)中的各列元素记为矢量 {σi}，i= 1,2，…q，在每个确定的τ处得出整个矢量空间的平均位移：

(6)

给定一个嵌入维数p，当S(τ)的值饱和时，此时的时间延迟τ即为对应嵌入维数p下的准最佳值。虽然没有得到时间延迟τ的最佳值，但在实际应用中准最佳值也是可以接受的。为得到准最佳时间延迟τ对应的准最佳嵌入维数，只需将τ代入式(4)就可以得到准最佳的嵌入维数。

2 基于动态聚类的奇异值分解重构

2.1 基于奇异值分解构造虚拟观测信号

根据矩阵理论，式(1)中的吸引子轨迹矩阵X的奇异值分解为

X=UΛVT。

(7)

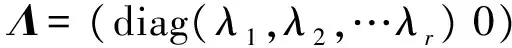
2.2 基于动态聚类的重构阶次确定方法

反映吸引子轨迹矩阵X特征的奇异值主要集中在若干幅值较大奇异值上，噪声的奇异值幅值相对较小。如果将奇异值投影到某一坐标轴上，反映信号特征的奇异值将分散在坐标轴上，而噪声信号的奇异值分布相对集中，将其作为奇异值的分布规律，对信号的奇异值进行聚类，较小奇异值会聚集在一起，而一些较大的奇异值会单独聚类。因此，可以认为单独成类的奇异值的个数为最佳重构阶次[8]。利用k-means方法对奇异值进行动态聚类，其具体计算过程如下：

1) 将样本划分为K个聚类区域，计算m1,m2,…mK和Je;

2) 任选其中的样本x∈ωi；

3) 如果Ni=1 ，则重新循环到步骤2)，如果Ni≠1，则循环到步骤4)中；

4) 计算下式的值：

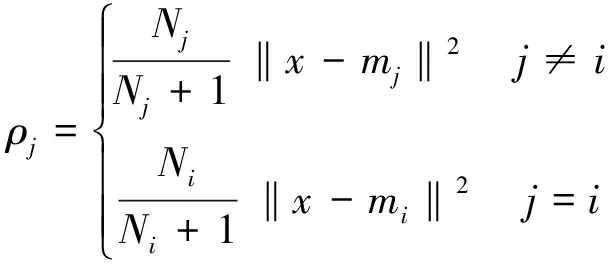
5) 对所有的样本进行计算，如果ρM≤ρj，则将x从ωi移到ωM中去;

6) 再次计算mi和mM的值，并修改聚类准则函数Je；

7) 将所有的样本循环迭代后，聚类准则函数Je的值如果仍然不变，则k-means聚类停止，聚类准则函数Je的值如果变化则循环到步骤2)。

3 仿真信号分析

3.1 相空间重构方法实例验证

为验证相空间重构中嵌入维数与重构阶数的有效性，对Lorenz吸引子方程得到的数据进行相空间重构。Lorenz吸引子方程为

(8)

式中：σ=10，R=30，b=5。

根据方程模型产生试验数据，采样时间ts=1s，采样点数为1 000个。图1示出广义嵌入窗长和自关联函数的关系，表1示出计算得到的准最佳嵌入维数与时间延迟，图2示出原始信号与不同准最佳嵌入维数与时间延迟下的重构信号及其频谱分布。

图1 Lorenz的广义嵌入窗长和自关联函数

编号嵌入维数给定值/维嵌入维数计算值/维时间延迟计算值/s12040．0482120170．0153220540．005

从图2可以看出:如果嵌入维数不满足嵌入定理，得到的重构信号误差较大；当满足嵌入定理后，维数在一定取值范围内，维数较高的重构信号精度更高。试验结果表明，在遵守嵌入定理的前提下，利用提出的算法得到了准最佳的嵌入维数与时间延迟。

图2 不同重构参数下的重构信号及其频谱

3.2 欠定盲源分离方法仿真试验

引入3个仿真源信号：s1=sin(20πt2),s2=sin(20πt)，s3为高斯白噪声。式中，t∈[0 1s] 。

构造观测矩阵A：

(9)

则观测信号Z为

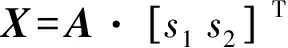
(10)

试验中构造3个仿真源信号，2个观测信号，模拟盲源分离中的欠定问题。各仿真信号的时域波形见图3。

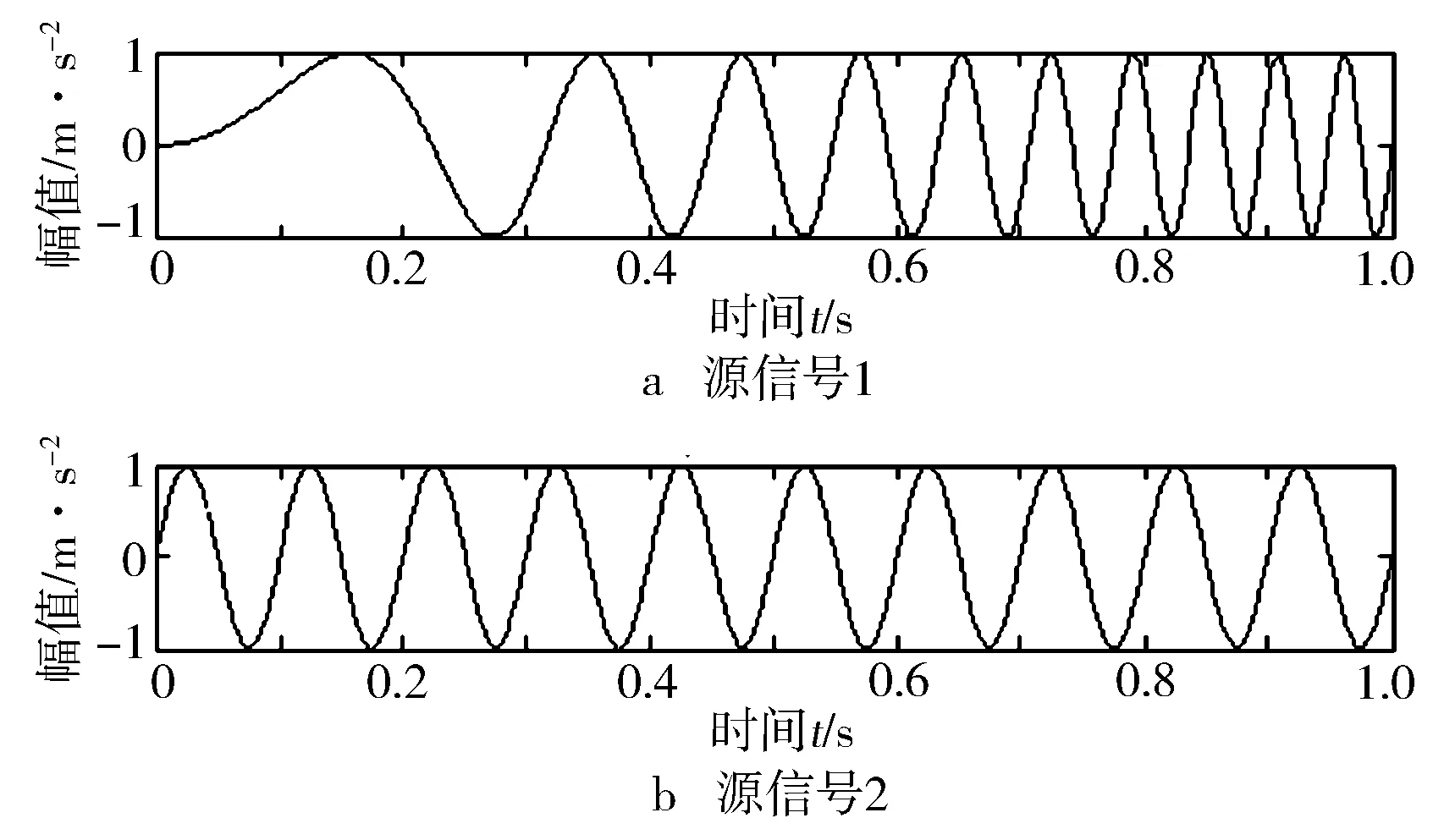
图3 源信号时域波形

图4示出第1个观测信号轨迹矩阵的奇异值分布，易确定最佳重构阶次为8。通过重构得到1个虚拟观测信号。

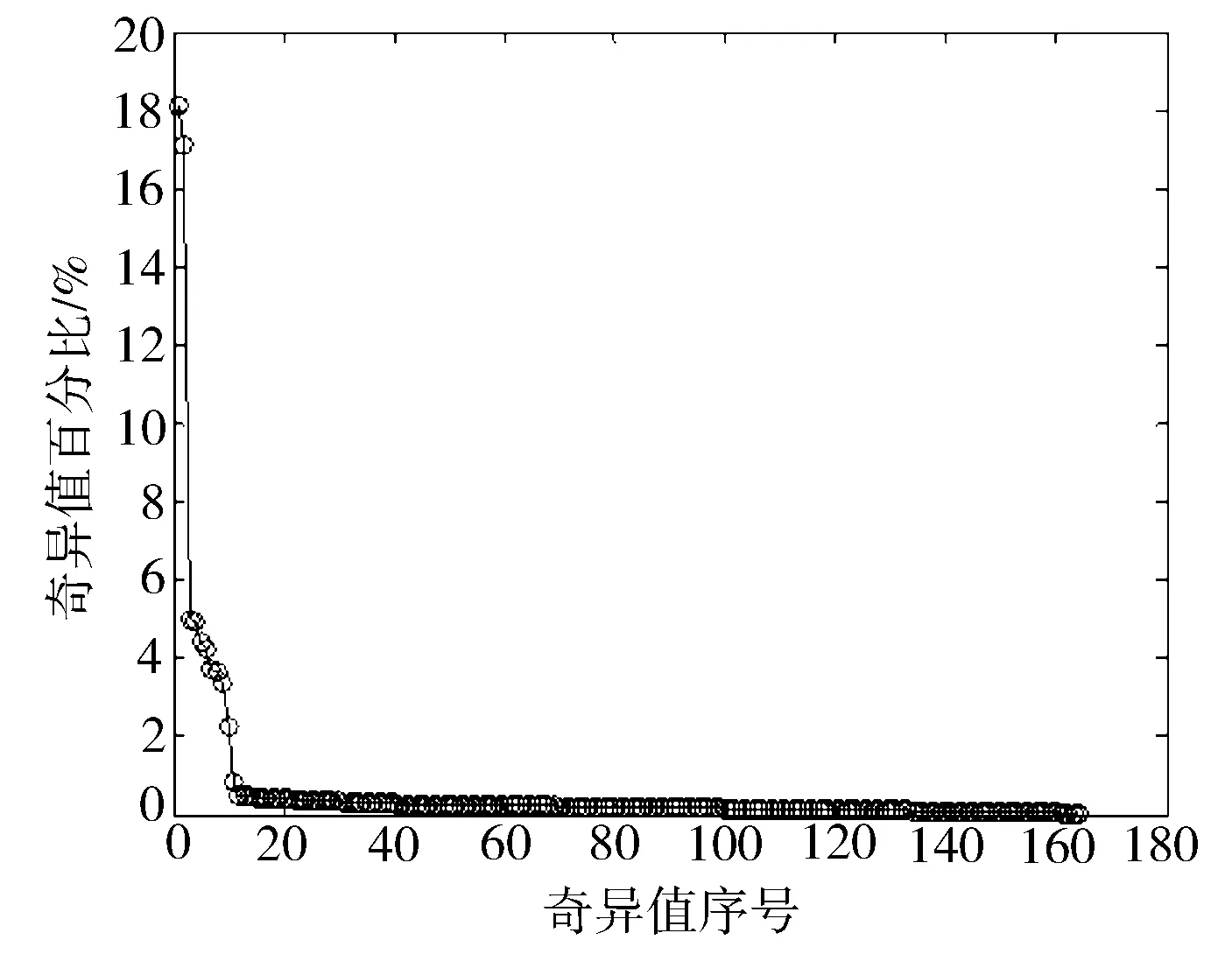
图4 观测信号轨迹矩阵的奇异值分布

图5示出实际观测信号与虚拟观测信号的时域波形。利用其组成混合信号，从而将观测信号的盲源分离从欠定变换为适定，满足了观测信号数不小于源信号数的基本要求。

图5 瞬时混合观测信号

将2个实际观测信号与虚拟观测信号组成传播路径，采用自适应Parafac方法对观测信号进行盲源分离，得到图6所示的分离信号。

图6 分离信号时域波形

比较图6和图3可知，从观测信号中很好地分离出了源信号。仿真结果表明，基于相空间重构和动态聚类奇异值分解的方法可有效获取虚拟观测信号，将欠定盲源分离转换为适定或超定，并准确分离出有效的源信号。

4 试验分析

4.1 柴油机曲轴轴承振动信号采集方案

试验在EQ6BT型6缸四冲程柴油机上进行，将振动传感器安装在油底壳与缸体结合部正对第4道主轴承左右处(测点Ⅰ、测点Ⅱ)和油底壳处(测点Ⅲ)(见图7)。

图7 传感器的安装位置

通过相关分析后发现测点Ⅰ、测点Ⅱ与内部激励源同方向信号的相关程度较高，而测点Ⅲ与内部激励源同方向信号相关程度不高[9-10]，因此，本试验选择将振动传感器安装在测点1(测点Ⅰ)、测点2(测点Ⅱ)处，并在各自下方不远处安装另外2个振动传感器，分别为测点3和测点4，在柴油机匀速状态下同步采集各振动信号，采样频率为20kHz。试验设置的曲轴轴承技术状态见表2。

表2 曲轴轴承故障设置

试验以第4道曲轴轴承为试验对象，通过设置不同轴颈与轴承的配合间隙来模拟磨损状态。为了模仿实际的曲轴轴承磨损故障，设置故障轴承间隙的同时，还需改变相邻两道轴承的间隙。试验安装的4个传感器离轴承故障振源较近，测量得到的信号对轴承配合间隙变化敏感[11]。

4.2 轴承故障诊断

曲轴轴承正常时4个测点的观测信号时域波形及其时频谱见图8。

图8 正常观测信号时域波形与时频分布

图9示出各测点正常观测信号的奇异值变化，此时假设有3个聚类中心，将奇异值分为4段，从高到低分别为第1，2，3和4段，利用第1段奇异值进行重构得到的信号称为重构信号1，其他以此类推。

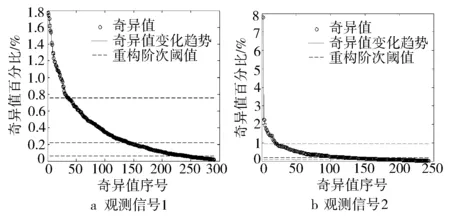
图9 各测点正常观测信号轨迹矩阵的奇异值分布

通过动态聚类分析分别得到4个观测信号的4段重构信号对应的奇异值重构阶次分段情况(见表3)。

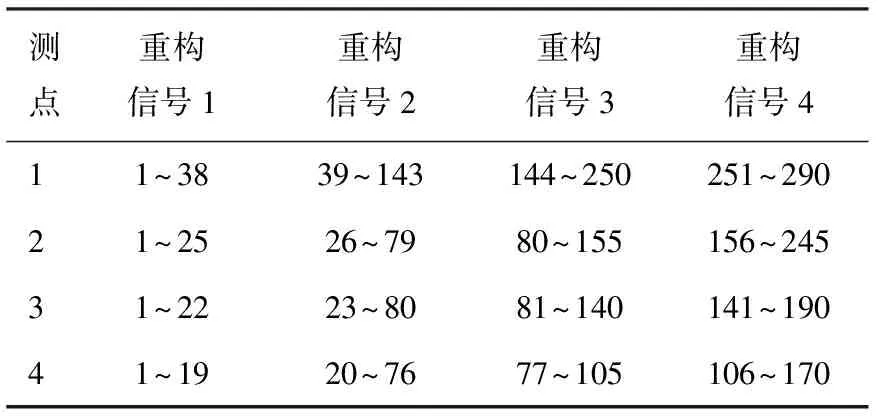
表3 信号重构阶次分段情况

图10示出各测点不同阶数重构信号的时频谱。从图中可以看出，正常观测信号的能量主要集中在重构信号1和重构信号2中。

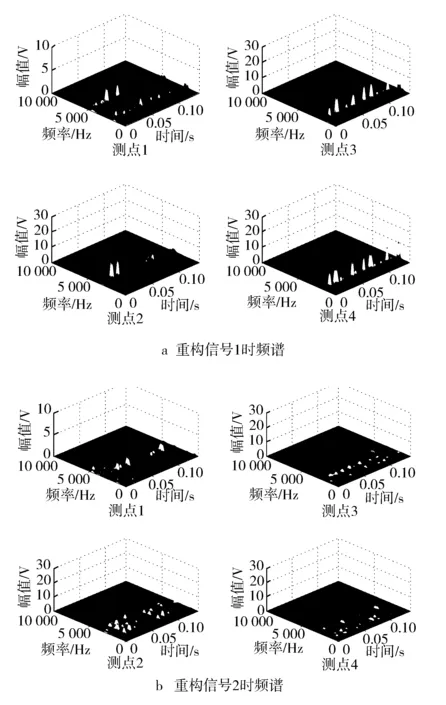
图10 正常状态各测点重构信号的时频谱

通过在信号时频图上对时间轴做切片来跟踪信号在某时刻的频率变化。图11示出信号能量最大时的切片，从图中可以看出，观测信号正常时各测点的重构信号1更接近原始信号在频率轴上的能量变化。

图11 正常状态各测点重构信号的时频谱切片

经分析可知，当曲轴轴承出现轻微故障、中度故障和严重故障时，振动信号的能量也主要集中于重构信号1与重构信号2中，且重构信号1的能量变化与原信号更接近。

以重构信号1和重构信号2组成奇异值分解矩阵，以奇异值的均值和脉冲指标组成特征向量，其空间分布见图12。

图12 重构信号1和2的奇异值特征向量空间分布

由图12可知，重构信号1和 2包含的信息与曲轴轴承振源信息有较强的相关性，但是还存在部分交叠，可能是信号在传输过程中存在延迟滤波造成的。因此，利用重构信号1和 2所在的重构阶次重构虚拟观测信号，从而将盲源分离从欠定变为适定，然后采用自适应Parafac盲源分离方法消除传输路径上的延迟滤波，得到分离信号的特征向量空间分布(见图13)。

图13 分离信号的奇异值特征向量空间分布

为定量描述故障诊断精度，定义诊断误差Ei为

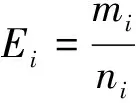
(11)

式中：样本号i=1,2,3,4，分别对应轴承正常、轻微故障、中度故障和严重故障；mi为样本i错误聚类点数；ni为样本i的点数。重构信号1和2特征值和分离信号特征值表征的整体故障诊断准确率分别为81.6%和100%。由此可知，基于盲源分离后信号的故障诊断准确率提高了18.4%。

5 结束语

通过引入广义嵌入窗长的概念，改进了相空间重构嵌入维数和时间延迟的自动算法，得到了准最佳嵌入维数和时间延迟值。提出基于动态聚类的奇异值分解重构算法，构造虚拟观测信号，从而将欠定盲源分离问题转变为适定或超定。将虚拟观测信号与原信号组成传播路径，利用自适应Parafac方法对实现了信号盲源分离。仿真与试验结果表明，本方法准确分离出了有效源信号，并将柴油机曲轴轴承故障诊断准确率提高了18.4%。

[1]GrondinO，ChauvinJ，GuilleminF，etal.Combustionparametersestimationandcontrolusingbibrationsignal：ApplicationtotheDiselHCCIengine[C]//Proceedingsofthe47thIEEEConferenceonDecisionandControl.Cancun：IEEE，2008.

[2]ZibulevskyM，PearlmutteB.Blindsourceseparationbysparsedecompositioninasignaldictionary[J].NeuralComputation，2001,13(4):864-880.

[3] 毋文峰，陈小虎，苏勋家，等.基于经验模式分解的单通道机械信号盲分离[J].机械工程学报，2011,47(4):12-16.

[4]ShinK，HammondJK，WhitePR.IterativeSVDmethodfornoisereductionoflow-dimensionalchaotictimeseries[J].MechanicalSystemsandSignalProcessing,1999,13(1):115-124.

[5] 杨绍清，贾传荧. 两种实用的相空间重构方法[J].物理学报，2002,51(11):2452-2456.

[6] 马红光，李夕海，王国华，等.相空间重构中嵌入维和时间延迟的选择[J]. 西安交通大学学报，2004,38(4):335-338.

[7] 修春波，刘向东，张宇河.相空间重构延迟时间与嵌入维数的选择[J].北京理工大学学报，2003,23(2):219-221.

[8] 王维，张英堂，徐章随. 基于动态聚类的奇异值分解降噪方法研究[J].振动工程学报， 2008,21(3):304-308.

[9] 梅检民，张玲玲，肖云魁，等.基于高阶累积量的轴承并发故障振动信号分析[J].内燃机学报，2011,29(4):327-331.

[10] 陆金铭.基于气缸盖振动信号的柴油机故障诊断研究[J].内燃机工程，2008,29(1):72-76.

[11] 肖云魁，曹亚娟，吴晓，等.用循环谱理论分析发动机曲轴轴承加速振动信号[J].振动、测试与诊断，2008,28(2):117-121.

[编辑: 李建新]

Fault Diagnosis for Crankshaft Bearing of Diesel Engine Based on Underdetermined Blind Source Separation

ZHU Jiangtao

(Shanxi Traffic Vocational And Technical College， Taiyuan 030031， China)

In order to solve the problems of underdetermined blind source separation for diesel engine crankshaft bearing vibration signal, a determined method based on singular value decomposition by using dynamic clustering and phase space reconstruction was proposed. A quasi-optimal embedding dimension and time delay values were first acquired through introducing the concept of generalized embedded window length in order to reconstruct phase space matrix. Then the singular value decomposition was applied to the matrix, the obtained singular values were conducted by using dynamic clustering to determine the optimal reconstruction order, the virtual observation signals were obtained, and hence the underdetermined problems became determined or overdetermined. Finally, the virtual observed signal and the original signal were composed into propagation paths so that the signal containing bearing fault characteristics was extracted by the blind source separation based on the algorithm of adaptive Parafac. The simulation results show that the method can extract the source signal from mixed signals effectively. The diagnosis accuracy increases by 18.4% by applying the method to diesel engine crankshaft bearing fault diagnosis.

vibration signal; underdetermined blind source separation; phase space reconstruction; singular value decomposition； dynamic clustering； fault diagnosis

2017-03-22;

2017-08-12

朱江涛(1981—)，男，讲师，主要研究方向为工程机械设计与运用；zhujtn@163.com。

10.3969/j.issn.1001-2222.2017.04.008

TK418

B

1001-2222(2017)04-0036-07