奎屯河流域春季融雪期SCS-CN模型参数取值方法

王瑾杰, 丁建丽, 张 喆,邓 凯,陈文倩, 张 成

1 新疆大学生态学博士后流动站， 乌鲁木齐 8300462 新疆交通职业技术学院，乌鲁木齐 8314013 新疆大学资源与环境科学学院，乌鲁木齐 8300464 新疆大学绿洲生态教育部重点实验室，乌鲁木齐 830046

奎屯河流域春季融雪期SCS-CN模型参数取值方法

王瑾杰1,2,3,4, 丁建丽1,3,4,*, 张 喆3,4,邓 凯3,4,陈文倩3,4, 张 成2

1 新疆大学生态学博士后流动站， 乌鲁木齐 8300462 新疆交通职业技术学院，乌鲁木齐 8314013 新疆大学资源与环境科学学院，乌鲁木齐 8300464 新疆大学绿洲生态教育部重点实验室，乌鲁木齐 830046

水资源是保障我国西北干旱半干旱地区生态环境安全的关键因素。以新疆奎屯河流域为例,通过修正SCS模型土壤持水量及初损率参数计算方法,寻找适用于干旱半干旱地区山区典型流域春季融雪期径流模拟模型,为流域掌握水资源量及生态用水提供决策依据。与以往研究不同之处在于：首先,引入度-日模型修正降水量参数,以满足流域降雨-融雪混合补给径流特征。其次,利用多期MODIS数据驱动的TS/VI特征空间理论结合土壤水分吸收平衡原理计算土壤持水量参数(S)；再运用聚类分析法对初损率(λ)取值方法进行改进。通过参数算法改进后的SCS模型,参数率定期和验证期纳什效率系数和相对误差系数分别为0.92和0.64,0.7%和-1.5%。结果表明：1)参数算法改进后SCS模型能实现奎屯河流域春季融雪期日径流模拟。2)利用遥感大尺度地表信息参数化技术反演SCS模型参数,实现了遥感数据为SCS模型提供大尺度空间数据的同时,间接实现了模型参数由点状数据向面状数据转化的可能；3)初损率(λ)多组取值法可有效提高干旱半干旱地区大尺度流域径流模拟精度。

奎屯河流域；融雪期；SCS-CN模型；参数算法改进；遥感

中国西北部干旱半干旱地区河流主要发源于山区,地表径流主要由高山带冰(川)雪融水、中山森林带降水和低山带基岩裂隙水等组成。长期依靠自然界独特的水循环过程维持着脆弱的平衡关系[1]。在全球气候变暖影响下,干旱区内陆河流域水资源的不确定性不断加剧,直接影响流域生态安全。尤其在山区及其周边流域,每年4—5月融雪期,径流时空分布差异显著,频繁发生的融雪型洪水,使流域大面积植被遭到破坏,水土流失严重,生态环境十分脆弱,给当地农业生产和人民生活带来巨大安全隐患。因此,定量研究山区流域地表径流,对认识流域水资源季节性变化规律,开展生态环境保护和防洪减灾工作具有重要意义。

在流域地表径流模拟过程中,SCS-CN模型(Soil Conservation Service Curve Number,简称SCS模型),是目前全球应用最为广泛的降雨-径流模型之一。由原美国农业部水土保持局(USDA-SCS)根据境内不同地区流域降雨-径流资料的搜集、整理、分析、研究得出的经验模型。具有结构简单、物理概念明确、所需参数少等特点,因被SWAT、Mike Hyro Basin等分布式水分模型应用于地表径流模拟而在世界范围内得到广泛应用。该模型主要研究集中于湿润地区,且深入研究者甚多[2- 5]。干旱半干旱地区也有应用,例如周淑梅、张秀英及李舟等人通过对模型的改进,分别在陕西、甘肃和西北高寒山区小流域模拟都取得了良好的效果[6- 9]。地域广阔的干旱区,流域尺度大,具有降雨、冰雪融水混合补给径流等特征,其地表径流模拟区别于单纯以降雨驱动的湿润地区小流域径流模拟；加之山区可达性差,人为观测极为困难,利用遥感大尺度信息观测优势结合水文模型,寻找适合于干旱半干旱区地表径流模拟方法,对当地生态环境、农业生产及人类生活具有重要现实意义。基于此,本文预借助遥感技术对SCS模型参数计算方法进行改进以提高径流模拟精度,具体改进方法如下：1)借助遥感大尺度地表空间信息参数化特性,结合MODIS卫星数据驱动的特征空间理论反演流域空间土壤含水量,再利用土壤水分吸收平衡原理,间接实现模型土壤持水量(S)空间数据的估算；2)针对流域降雨、融雪混合补给径流特征,引入度-日模型,将降水量参数修正为降雨与积雪消融水当量之和；3)采用聚类分析法将参数率定期初损率(λ)进行聚类,选择多组λ值进行模拟,以提高模拟精度。小流域SCS模型应用时汇流时间较短可忽略汇流项,大尺度流域SCS模型应用要确保汇流时间小于24 h。

1 数据与方法

1.1 研究区概况

图1 奎屯河流域示意图Fig.1 Watershed location of Kuitun river basin

本文以新疆天山支脉依连哈比尔尕山北麓奎屯河流域为研究区(图1),流域面积1945km2,位于83°30′—85°08′′E,43°30′—45°00′′N之间,是天山北坡中段仅次于玛纳斯河流域的第二大流域。集水区面积较大,年平均气温9℃,海拔为1121—4909m,其中海拔3700m以上为冰川及永久性积雪覆盖,致使流域径流补给多样,既有高山冰川和永久性积雪融水补给,又有中低山区降雨和季节性冰雪融水补给。每年4—5月为流域春季典型融雪期,径流补给以积雪融水为主,降雨为辅。,当气温骤然上升时会引发季节性融雪洪水。基于以上特征,本文选取流域出山口将军庙水文站2005—2007年日观测数据,模拟奎屯河出山口4—5月地表径流量,为周边灌区及城市的防洪减灾和水资源分配提供参考依据。

1.2 数据资料

奎屯河流域水文模拟需要的基础地理数据包括：气象、水文、卫星遥感影像等多源数据类型。其描述和来源见表1。其中,为获取研究区参数率定期地表温度及植被指数月均值数据,需下载空间分辨率为1 km的MODIS陆地3级标准数据产品MOD13A3和MOD11A2,并对数据进行预处理,包括对数据进行投影转换、几何校正和矢量边界裁剪等,得到覆盖全区的栅格数据。已有大量研究证实MODIS卫星产品精度能有效反映区域地表温度及植被指数情况[9- 10]。

表1 奎屯河流域基础地理数据

2 研究方法

2.1 SCS模型原理

SCS模型是基于水量平衡方程(1)存在的[11]：

P=Ia+F+Q

(1)

式中，P为总降雨量(mm)；Ia为地表径流生成前降雨量初损值,包括地面填洼、截留、表层蓄水和下渗的初损量(mm)；F为地表径流生成后的后损(mm),即实际累积下渗量(不包括Ia)；Q为地表径流量(mm)。

与此同时,Mockus等人通过大量实测数据分析建立了降雨-径流关系式：

(2)

式中,S为土壤当时最大可能持水量,是后损的上限(mm)。 由于式中Ia数据不易获取,通常引入参数初损率(λ),建立Ia与S的线性关系式：

Ia=λS

(3)

式中,λ为初损率,具有区域化特征。将方程(2)、(3)带入(1)中得SCS径流模拟核心方程为：

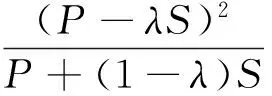
(4)

式中,Q为地表径流深(mm)；P为总降水量(mm)；S为当时最大可能持水量 (mm)。λ为初损率。其中S值通常由CN计算而得,计算方法如方程(5)所示：

(5)

式中,CN值为径流曲线数,通常由土地利用方式、土壤质地和降雨事件前期土壤湿润情况(antecedent moisture condition,AMC)等数据来确定。其详细分类标准可参考美国《国家工程手册》[12]。

初损率(λ)通常取标准值0.2进行计算；但由于不同流域具有一定的时空差异,λ值取标准值不能满足不同流域的需求,本文利用实测降雨、径流数据和计算S值结合公式(6)对初损率(λ)进行参数率定,具体方法如下：

(6)

式中,P1、Q1分别为模型参数率定期流域实测日降水量(mm)和日径流量(mm)。

2.2 SCS模型参数计算方法的改进

2.2.1 降水量计算方法的改进

由于原有SCS模型对降雨量具有一定条件限制,即模型认为当降雨量(P)大于λS时,产生地表径流,否则地表径流量为零。该条件使SCS模型无法应用于降雨量稀少的干旱半干旱地区。本文根据研究区4—5月降雨和积雪融水混合补给径流的特点,将SCS模型降水量修正为流域降雨量与积雪消融水当量之和,如方程(7)所示。

P=Pr+Ps

(7)

式中,P为SCS模型径流方程输入的总降水量(mm)。Pr为实测日降雨量(mm)；Ps为日积雪消融水当量(mm),引入度日模型进行计算。

度-日模型是基于冰雪表面温度建立的冰雪融水当量计算模型。广泛应用于北欧、阿尔卑斯山、青藏高原等地区的冰雪消融研究中。优点在于模型计算简单、参数容易获取且计算精度较高。因此,本文引入度-日模型计算研究区4—5月积雪消融水当量,具体计算方法如下：

Ps=DDF×PDD

(8)

式中,Ps为日积雪消融的水当量(mm)；DDF为冰川或雪的度日因子(mm d-1℃-1),利用张勇[13]等人根据海拔对中国西北地区冰、雪度日因子计算结果,采用克里格空间插值法计算而得；PDD为某一时段内的正积温,PDD可通过下式计算：

(9)

式中,Tt为某时段的平均气温(℃)；Ht为逻辑变量,当Tt≥0℃时,Ht=1.0；当Tt≤0℃时,Ht=0.0。

2.2.2 土壤持水量(S)计算方法的改进

原有SCS模型S值是通过CN值进行计算的,存在涉及参数多,数据难以获取且计算过程复杂等问题。与传统方法相比,本文改进之处在于,首次利用遥感及Ts-VI特征空间理论反演土壤含水量参数结合土壤水分吸收平衡原理计算S值[14],计算方法如下：,

S=Wmax-Wsoil

(10)

式中，S值为当时最大可能持水量；Wmax为土壤饱和含水量,通过测定野外土壤样品的土壤孔隙度和土壤容重计算而得,由于数据缺乏,本文取最大值 100%[19];Wsoil为平均土壤含水量；本文Wsoil为研究区参数率定期2005—2006年4—5月土壤含水量月平均值,是利用MODIS卫星数据产品地表温度(Ts)和归一化植被指数(NDVI)构建的温度-植被干旱指数(Ts-VI)特征空间理论进行估算的。为使SCS模型中参数单位统一为mm,需用水层厚度将土壤含水率转换为土壤含水量,mm,进行计算。

Moran[15]等人在地表温度(Ts)、植被指数(VI)与土壤湿度(water content of soil, SRWC)之间关系研究中发现,土壤湿度与二者变化具有极为密切的关系,若将区域内每个像元的VI值作为x轴,Ts作为y轴,可构建出呈现阶梯状的特征空间二维散点图,散点图的两条边界线分别代表区域土壤湿润程度的干边和湿边,再通过干、湿边方程系数结合NDVI计算得到温度植被干旱指数TVDI值,该值可直接反映地表土壤水分情况,计算得到任一点的TVDI值介于0和1之间。TVDI值越大,代表土壤含水量越低,反之土壤含水量则越高。

为了使计算结果更接近实测值,将TVDI值与实测土壤水分值进行拟合修正,最终得出区域土壤水分(SRWC)值。其中,TVDI计算公式如下：

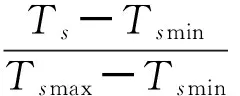
(11)

式中，Tsmax和Tsmin分别表示区域相同植被指数条件下所对应的最高温度和最低温度,计算公式如下：

Tsmax=aVI+b;Tsmin=cVI+d;

(12)

式中,a、b、c、d分别为干、湿边拟合方程系数。

最后,根据公式(13)(14)求算出研究区土壤含水量(SRWC)[16]

SRWC=SRWCW-TVDI(SRWCW-SRWCD)

(13)

式中,SRWCw为湿边上对应的最大值,取水体湿度100%。SRWCD为干边上对应的最小值,计算公式为：

SRWCD=(100-(100-Yi)/Xi)/100

(14)

式中,Xi为对应该点植被全覆盖像元TVDI值,Yi为对应该点的实测SRWC值。

2.2.3 初损率(λ)计算方法的改进

目前,已有的λ值算法有3种方法。即标准值法(λ=0.2)、事件分析法和反算法,反算法应用较多,即：每一组降水、径流数据结合S值可计算出与之一一对应的λ值,再通过计算λ的中值、众数、平均值等数学方法选取模拟精度最高的,作为最终唯一的λ取值。

本文改进之处在于,利用聚类分析法将降水、径流事件结合公式(6)计算所得的若干λ值进行聚类分析,得到30组不同的聚类中心值,并将这30组聚类中心值作为流域的λ取值库,再根据迭代次数计算的初始中心最小距离将所有λ值及其对应的降水、径流事件分别归类到这30组数据中,使每组降水、径流数据都有与之对应的聚类中心λ值,该方法与传统λ取唯一值相比,模拟结果更接近实际值。

3 参数算法改进后模型参数率定

3.1 降水量参数的确定

奎屯河流域降水量为降雨量和积雪消融水当量之和,结合流域2005—2007年4、5月实测降雨量和温度数据,计算出该时段的修正降水量见图2,图中绘制了183d的降水量修正值,其中降水量为0值代表该日气温在0℃以下且无降雨。此外,由于积雪融水当量的主要决定因素是温度,而研究流域的日平均气温从4月到5月是呈现逐步上升趋势的,因此所有年份修正降水量的分布都表现为4月小于5月。

图2 奎屯河流域2005—2007年4、5月降水量修正值Fig.2 Modified precipitation of Kuitun River Basin in April and May from 2005 to 2007

3.2 S值的确定

采用2005—2006年4、5月122d日数据作为SCS模型的参数率定期计算当时最大可能持水量(S)值。

3.2.1 流域边界的确定

利用研究区30m分辨率DEM数据,借助Mike Hyro Basin软件,生成流域边界(图3)。

3.2.2 地表温度及植被指数计算

按流域边界提取奎屯河流域2005—2006年4月—5月共32期地表温度和归一化植被指数,生成流域2005—2006年4—5月平均地表温度空间分布图和归一化植被指数空间分布图(图4，图5)。

3.2.3 TVDI计算

(1)计算干、湿边方程

利用TS-VI特征空间理论,结合生成的2005—2006年4—5月平均地表温度和平均归一化植被指数空间分布图生成二维散点图和拟合方程,并结合公式(11)计算出研究区2005—2006年4—5月平均TVDI空间分布图(图6)。

(2)土壤含水量计算

由于流域可达性较差,使野外采样点布设受限,现有野外实测数据为2005、2006年4、5月研究流域将军庙水文站周边13个土壤剖面0—10cm实测土壤含水量(SRWC)值,样点布设为每隔1km进行一次采样,每个采样点采取3次重复采样的方法,将重复采样土壤样本研磨均匀混合装铝盒后称重,带回实验室采用烘干法测定样本土壤含水率。然后根据方程(13)计算出流域2005—2006年4—5月平均土壤含水量空间分布图(图7)。

图4 奎屯河流域2005—2006年4—5月平均地表温度空间分布Fig.4 Spatial distribution of average land surface temperature in April and May from 2005 to 2006 in kuitun river basin

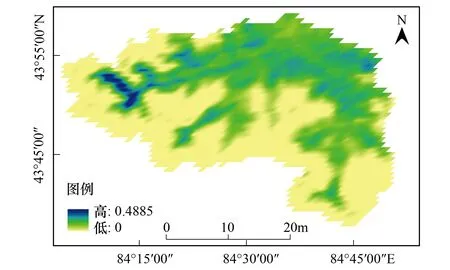
图5 奎屯河流域2005—2006年4—5月平均归一化植被指数空间分布Fig.5 Spatial distribution of average NDVI in April and May from 2005 to 2006 in kuitun river basin

图6 奎屯河流域2005—2006年4—5月平均TVDI值空间分布Fig.6 Spatial distribution of TVDI in April and May from 2005 to 2006 in Kuitun River Basin

图7 流域土壤含水量SRWC值空间分布Fig.7 Soil moisture spatial distribution of study area

图8 土壤含水率实测值与模拟值相关分析 Fig.8 Correlation analysis of soil moisture between measured and simulated value

关于遥感反演土壤含水量精度是否可靠,采用计算值与实测值对比的方法进行验证。即用野外实测采样点坐标提取SRWC空间分布图中对应的值,并与实测土壤含水量进行相关分析(图8),得相关系数r为0.7406,相对误差系数RE为-1.3%,该结果表明,遥感反演土壤含水量精度可靠。

利用计算所得流域平均土壤含水量值结合公式(10),初步确定奎屯河流域4—5月SCS模型参数当时最大可能持水量(S)值为80.5mm。

3.3 初损率(λ)的确定

根据计算所得S值和流域参数率定期及验证期183d修正降水量和观测径流量数据结合公式(6)计算出183组初损率(λ)值,以模型次降水量大于下渗量(λS)产生地表径流为边界条件,筛选出参数率定期112组、验证期58组符合模型条件的降水事件。再利用聚类分析法将参数率定期112组λ值进行聚类,计算出30组聚类中心λ值及与之对应的聚类成员,将这30组数据作为流域初损率(λ)取值库,参数率定期径流模拟时,将分类好的30组聚类成员分别带入对应的聚类中心λ值进行模拟即可；验证期径流模拟时,在取值库中选择与其计算λ值最为接近的聚类中心λ值进行模拟即可。对干旱区大尺度流域而言,λ取值库的建立较传统单一取值法模拟精度更高。

4 模拟结果检验与分析

本文利用改进后SCS模型对奎屯河流域参数率定期(2005—2006年4、5月)112场降水事件和验证期(2007年4、5月)58场降水事件进行径流模拟,模拟与实测径流结果如图9所示。

图9 奎屯河流域参数率定期改进模型模拟值与实测值及同期降水量分布Fig.9 Compared of observed and simulated runoff by calibration periods

图10 奎屯河流域验证期改进模型模拟值与实测值及同期降水量分布Fig.10 Compared of observed and simulated runoff by validation periods

图9、图10分别绘制了模型参数率定期和验证期模拟值与实测值结果。从模拟结果来看,两个时期模型参数算法改进后的模拟值与实测值总体变化趋势一致,且与流域降水量分布呈正相关。关于模拟结果的精度检验,本文选取了Nash-Sutcliffe效率系数和相对误差系数RE来反映模型模拟值和实测值的拟合程度及误差率(表2)。Nash-Sutcliffe效率系数经常被用来作为水文模型的效率评价指标,其变化范围为-∞到1。1值对应于实测值和模拟值的完美匹配；效率为0表明该模型模拟结果等同于实测值的均值系列,当NSE大于0.75时可认为模型模拟结果好[17],对比分析模型参数率定期和验证期NSE值发现,参数率定期模拟值与实测值匹配程度较高,模拟结果效果很好；验证期NSE值略低,说明验证期模拟精度还有待进一步提高。相对误差系数(RE)是最能反映模拟值可信度的,值越接近于0,则说明模拟值越接近实测值。模型参数率定期和验证期相对误差系数RE分别为0.7%和-1.3%,以RE低于±30%为标准[18],检验模拟结果误差范围在可利用范围。

分析误差产生的来源主要包括以下几个方面：

(1)计算S值产生的误差。模型S值的决定性变量是土壤含水量和土壤饱和含水量。土壤饱和含水量取最大值1,会导致S值偏大引起模拟值偏小的误差。因此,增加土壤含水量和土壤饱和含水量野外实测数据量可有效提高S值的精度。但是由于研究流域可达性差,探讨如何提高遥感大尺度观测数据精度将会成为干旱区大流域径流模拟的关键技术。

表2 参数算法改进后模型模拟值效率系数NSE、相关系数r和相对误差系数RE

Table 2 NSE(Nash-Sutcliffe efficiency coefficient)、r(correlation coefficient) and RE(relative error coefficient)for simulation performance assessments

评价指标Assessmentindexes参数率定期Calibrationperiods验证期Validationperiods纳什效率系数Nash-Sutcliffeefficiency0.920.64相对误差Relativeerror/%0.7-1.3

(2)计算降水量造成的误差。基于流域特殊径流补给方式,改进模型中的降水量参数被修正为积雪消融水当量和实测降雨量之和。其中,积雪消融水当量的决定性变量是温度,而流域内唯一的观测站气温数据不足以代表流域平均气温,而积雪消融水当量对气温变化较为敏感,流域温度每变化±1℃,积雪消融水当量变化±3.1 mm,如何获取准确且具有代表性的流域气温数据也是提高模拟精度的关键。增加实测观测站点的布设,受到地理位置和经费等问题的限制；就目前已有技术而言,可利用MODIS日数据产品提取流域温度图,获取流域平均温度,从而实现大尺度流域气温空间数据的获取。

(3)流域地处山区,海拔高,山区面积大,分布有冰川,流域基础地理数据和野外实测数据获取十分困难。因此,长时间序列野外数据的缺乏也是造成模拟误差的重要方面。

因此,在今后的研究中,探索卫星数据和遥感技术在水文模型中的应用,增加野外实测数据量等都是提高径流模拟精度的有效保障。

5 结论

(1)为了使SCS模型适用于奎屯河流域径流补给特征,引入度-日模型修正降水量参数,有效解决了因降雨量稀少导致模型在干旱半干旱地区大尺度流域无法应用的瓶颈。

(2)通过MODIS卫星数据结合Ts-VI特征空间理论反演流域土壤含水量的方法,集成了遥感信息空间数据的时空分布特性,间接实现了SCS模型参数由点状数据向面状数据的转换。

(3)原始SCS模型计算土壤持水量(S)参数涉及土地利用方式等5个参数及CN值对照表,利用遥感数据计算S值,具有涉及参数少且参数易获取的优势,可有效解决无资料地区模型应用数据缺乏的难题。

(4)初损率(λ)作为SCS模型重要的输入变量,具有时空变化特性,采用聚类分析法建立流域λ取值库的方法,使模型在描述流域水循环过程时更接近实际,其模拟结果较取唯一值的传统方法模拟精度有较大幅提高,使模拟过程也更加合理。

(5)参数算法改进后SCS模型参数率定期、验证期NES(nash-sutcliffe efficiency)和RE (relative error)分别为0.92,0.64和0.7%,-1.3%。参数改进算法拓展了SCS模型的适用范围,可为其他干旱半干旱地区下垫面条件相似流域的径流模拟提供参考。

[1] 陈亚宁, 李稚, 范煜婷, 王怀军, 方功焕. 西北干旱区气候变化对水文水资源影响研究进展. 地理学报, 2014, 69(9): 1295- 1304.

[2] Ponce V M, Hawkins R H. Runoff curve number: has it reached maturity?. Journal of Hydrologic Engineering, 1996, 1(1): 11- 19.

[3] Mishra S K, Singh V P, Sansalone J J, Aravamuthan V. A modified SCS-CN method: characterization and testing. Water Resources Management, 2003, 17(1): 37- 68.

[4] 林凯荣, 何艳虎, 陈晓宏. 气候变化及人类活动对东江流域径流影响的贡献分解研究. 水利学报, 2012, 43(11): 1312- 1321.

[5] 史培军, 袁艺, 陈晋. 深圳市土地利用变化对流域径流的影响. 生态学报, 2001, 21(7): 1041- 1049.

[6] 周淑梅, 雷廷武. 黄土丘陵沟壑区典型小流域SCS-CN方法初损率取值研究. 中国农业科学, 2011, 44(20): 4240- 4247.

[7] 张秀英, 孟飞, 丁宁. SCS模型在干旱半干旱区小流域径流估算中的应用. 水土保持研究, 2003, 10(4): 172- 174, 249- 249.

[8] 李舟, 董增川. 基于网格坡向要素影响的分布式水文模型研究应用. 水利学报, 2007, (S1): 500- 503.

[9] 袁敏, 肖鹏峰, 冯学智, 朱榴骏. 应用MODIS地表温度产品估计新疆典型区气温. 遥感信息, 2015, 30(1): 81- 89.

[10] 廖清飞, 张鑫, 马全, 姚瑶, 于东平. 青海省东部农业区植被覆盖时空演变遥感监测与分析. 生态学报, 2014, 34(20): 5936- 5943.

[11] 李润奎, 朱阿兴, 陈腊娇, 刘军志, 宋现锋, 林耀明. SCS-CN模型中土壤参数的作用机制研究. 自然资源学报, 2013, 28(10): 1778- 1787.

[12] 王瑾杰, 丁建丽, 张成, 张喆. 基于SCS模型的新疆博尔塔拉河流域径流模拟. 农业工程学报, 2016, 32(7): 129- 135.

[13] 张勇, 刘时银. 度日模型在冰川与积雪研究中的应用进展. 冰川冻土, 2006, 28(1): 101- 107.

[14] 王建, 丁永建, 刘时银. 高寒草地春季积雪融水和雨水混合补给径流模拟. 干旱区地理, 2005, 28(4): 460- 464.

[15] Moran M S, Clarke T R, Inoue Y, Vidal A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sensing of Environment, 1994, 49(3): 246- 263.

[16] Gillies R R, Kustas W P, Humes K S. A verification of the ‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface e. International Journal of Remote Sensing, 1997, 18(15): 3145- 3166.

[17] 魏冲, 宋轩, 陈杰. SWAT模型对景观格局变化的敏感性分析——以丹江口库区老灌河流域为例. 生态学报, 2014, 34(2): 517- 525.

[18] 符素华, 王向亮, 王红叶, 魏欣, 袁爱萍. SCS-CN径流模型中CN值确定方法研究. 干旱区地理, 2012, 35(3): 415- 421.

Calibration of SCS model parameters regarding snowmelt season in Xinjiang Kuitun River basin

WANG Jinjie1,2,3,4, DING Jianli1,3,4,*,ZHANG Zhe3,4, DENG Kai3,4, CHEN Wenqian3,4, ZHANG Chen2

1 Ecological postdoctoral research station, Xinjiang University, Urumqi 830046, China2 Xinjiang Vocational and Technical College of Communications, Urumqi 831401, China3 College of Resources and Environment Science, Xinjiang University, Urumqi 830046, China4 Key Laboratory of Oasis Ecology of Ministry of Education, Xinjiang University, Urumqi 830046, China

Water resources are key factors of ecological environmental security in northwest arid region of China. They are also the most important factors for socio-economic development against the background of global warmer, especially in arid regions. It is necessary for arid regions to calculate total water resources because it can provide a reference for the government with which to formulate strategies. Water resources may have a large area and be supplied by runoff from mountain snowmelt and precipitation. The goal of this paper was to determine the suitable method to simulate runoff in arid areas. The Soil Conservation Service Curve Number (SCS-CN) developed by the U.S. Department of Agriculture National Resources Conversion Service (NRCS) is the most popular and widely applied model for direct runoff estimation. This method was modied by accounting for the static portion of inltration and the antecedent moisture. This model has stimulated a great deal of discussion among scientists and hydrologists. The model is based on the water balance equation and curve number CN, which is derived from the tables given in the National Engineering Handbook for catchment characteristics, such as soil texture, land use, hydrologic condition, and initial soil moisture condition. Based on the spatiotemporal differences among watersheds, international and domestic academics have developed different methods to improve the SCS-CN model. One option is to improve its mechanism and another is to improve the parameter calculation methods. Because there is considerable scope to improve the SCS-CN model, we discuss a parameter algorithm to improve the method for snowmelt and precipitation mix and large-scale basins in arid regions as a solution to a major problem. This study focused on the Kuitun River Valley. We explored the adoption of an SCS model runoff simulation in arid and semi-arid regions with snow-melt and rainfall in spring by modifying the calculation method of SCS model parameters. To satisfy the characteristic of mix supplied runoff, precipitation was revised to represent the sum of rainfall and snowmelt. The snowmelt was calculated by the degree-day model. This was the first time MODIS satellite products with approximately 1km resolution were used to invert the Land Surface Temperature and Normalized Difference Vegetation Index. Then, we used the surface temperature/vegetation index (TS/VI) constructed in a 2D scatter plot. The combined soil moisture absorption balance principle was used to calculate the moisture-holding capacity of soil. We used cluster analysis to modify the initial abstraction computing methods. The calibration and validation periods of Nash-Sutcliffe efficiency were 0.92 and 0.64, respectively. Relative errors were 0.7% and -1.3%, respectively. This indicated that the improved model was effective in simulating spring runoff in the Kuitun River Valley. Using remote sensing parameter information technology to improve the SCS model can indirectly implement data conversion from point to plane. Establishing a database of the initial abstraction can improve the precision in effectively simulating runoff in large-scale basins in arid and semi-arid regions. To circumvent the bottleneck caused by lack of data, reference to simulated runoff can be used under similar basin conditions in data-lacking regions.

Kuitun River basin; snowmelt period; SCS-CN model; improved algorithm of parameters; remote sensing

国家自然科学基(U1303381,41261090)；自治区重点实验室专项基(2016D03001)；自治区科技支疆项目(201591101)；教育部促进与美大地区科研合作与高层次人才培养项目

2016- 03- 15; 网络出版日期:2017- 02- 23

10.5846/stxb201603150464

*通讯作者Corresponding author.E-mail: watarid@xju.edu.cn

王瑾杰,丁建丽,张喆,邓凯,陈文倩, 张成.奎屯河流域春季融雪期SCS-CN模型参数取值方法.生态学报,2017,37(13):4456- 4465.

Wang J J, Ding J L, Zhang Z, Deng K, Chen W Q, Zhang C.Calibration of SCS model parameters regarding snowmelt season in Xinjiang Kuitun River basin.Acta Ecologica Sinica,2017,37(13):4456- 4465.