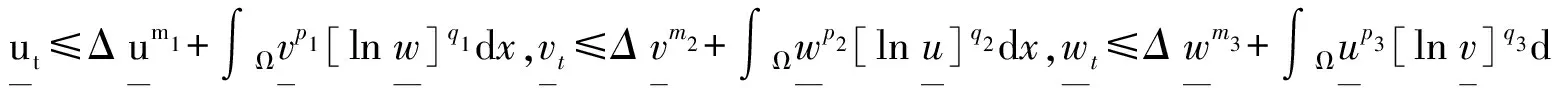一类交叉耦合抛物方程组解的整体存在及爆破

薛应珍

(西安外事学院 商学院, 陕西 西安 710077)

一类交叉耦合抛物方程组解的整体存在及爆破

薛应珍

(西安外事学院 商学院, 陕西 西安 710077)

为了更好描述3种混合物质燃烧的热传导过程，或者化学反应中3种反应物的反应情况，研究了一类具有3个变量交叉耦合且带有非局部源及非局部边界流抛物型方程组解的整体存在及有限时刻爆破问题,打破常用的第一特征值等构造上下解的方法，而采用常微分方程方法构造了该方程组的上、下解，引用比较定理，证明得到了由幂函数局部源和指数函数非局部源交叉耦合的退化抛物型方程组解的整体存在及解在有限时刻爆破的充分条件，为热传导和化学反应问题提供更好的理论支持.

交叉抛物型方程组；比较原理；整体存在；爆破

针对交叉耦合的抛物方程组解的渐近性态问题，许多学者已做了大量研究，文献[1]研究了具有3个变量交叉耦合的局部源和非局部边界抛物型方程组解的渐近性态，得到了解整体存在及有限时刻爆破的充分条件.文献[2]研究了具有2个幂函数作为局部源耦合的抛物型方程组解局部存在、整体存在和全局爆破的充分条件.文献[3]将文献[2]的结论进行了推广.文献[4-6]研究了具有幂函数耦合抛物型方程组解的渐近性态.文献[7]研究了一类拟线性抛物型方程组解在有限时刻爆破的充分条件及同时爆破的充分必要条件. 文献[8-19]研究了其他如具有非局部吸收源等交叉耦合的抛物型方程组解的渐近性态等.

基于以上工作，本文研究了如下由幂函数和对数函数的非局部源交叉耦合，且具有3个变量交叉耦合退化抛物型方程组解的整体存在及解在有限时刻爆破的充分条件.

(1)

具有非局部边界流

(2)

及连续有界初值

(3)

1 预备知识

(4)

具有非局部边界流

(5)

及连续有界初值

(6)

由文献[20],有如下的比较引理:

2 解的整体存在

定理1 如果m1m2m3>p1p2p3+q1q2q3+3，对于小初值u0(x)、v0(x)、w0(x)，方程组(1)-(3)的解整体存在.

证明：设φ(x)满足

(7)

ap3bq3K1(p3m2+q3m1)/m1m2Ω.

综上可知，只要存在a、b、c，使得

(8)

下证这样的a、b、c存在.令bp1=am1c-q1K1-(p1m3+q1m2)/m2m3Ω-1ε0，将此式代入式(8)中，可得关于a的不等式

(9)

由定理1条件知m1m2m3>p1p2p3+q1q2q3+3，(m1m2-p1q2)(m3p1+q1q3)>(p1q2+m2q1)·(p1p3+m1q3)，只要取a充分大时，可使得式(9)成立.另只要a、b、c充分大，又对于小初值u0(x)、v0(x)、w0(x)，就可以保证式(8)的后3个式子成立.定理1证毕.

3 解的有限时刻爆破

讨论解的整体存在问题时，引入以下2个引理:

引理3 设θ>λ>1，k、l>0,h(t)是问题

(10)

的正解，则当h0充分大时，h(t)>2在有限时刻爆破.

引理4 设λ2>λ1>1,Q2>Q1>1，则引理3的(h(t))满足

引理3及引理4的证明见文献[5].

定理2 如果m1m2m3

证明：设φ(x)是满足方程

(11)

的解，则存在C>2,使得0≤φ(x)≤C.令

其中：l1、l2、l3均大于1，h(t)待定，由式(10)-(11)可知，hliφl2(x)>2(i=1,2,3),则对于任意正实数α，利用拉格朗日中值定理证明可知lnα[hli(t)φli(x)]>h-αli(t)φ-αli(x)，记

∫Ωhl2p1(t)φl2p1(x)lnq1(hl3(t)φl3(x))dx≤l1hl1-1(t)φl1(x)h'(t)-

l1m1(l1m1-1)hl1m1(t)φl1m1-2(x)Δφ(x)-∫Ωhl2p1(t)φl2p1(x)h-l3q1(t)φ-l3q1(x)dx=

l1hl1-1(t)φl1(x)[h'(t)+m1(l1m1-1)hl1m1-l1+1(t)φl1m1-l1-2(x)-

综上由引理3的条件可知，只要存在l1、l2、l3，使得

(12)

成立.则由引理4知，存在满足引理3的h(t)使得

(13)

由定理2条件m1m2m3

(q1q2+m1p2)(p1p3-m1q3)>(p1q2+m1m2)(m1m2+p3q1).

即式 (13)成立，定理2证毕.

[1] 吴春晨.一类非局部边值条件抛物型方程组解的性质[J].江南大学学报(自然科学版)，2015，14(2):222-225. DOI:10.3969/j.issn.1671-7147.2015.02.018. WU C C. A nonlinear parabolic system with nonlocal boundary conditions[J]. Journal of Jiangnan University( Natural Science Edition), 2015，14(2):222-225. DOI:10.3969/j.issn.1671-7147.2015.02.018.

[2] 宋慧，曾有栋.具有非局部边界和局部化源拋物方程组解的全局存在与爆破性[J].生物数学学报，2014,29(4)：711-717. SONG H, ZENG Y D. Global blow-up for a localized nonlinear parabolic system with a nonlocal boundary condition[J]. Journal of Biomathematics, 2014,29(4)：711-717.

[3] 吴春晨.一类非局部边值条件抛物型方程组解的性质研究[J] .郑州大学学报( 理学版),2014,46(4):18-22。 WU C C.The properties of solutions for a nonlinear parabolic system with nonlocal boundary conditions[J] .Zhengzhou Univ ( Nat Sci Ed ) ,2014,46(4):18-22.

[4] 樊彩虹，容跃堂，房春梅，等.退化反应扩散方程组解的整体存在和有限爆破[J].纺织高校基础科学学报，2016,29(1): 35-38. DOI:10.13338/j.issn.1006-8341.2016.01.006. FAN C H,RONG Y T,FANG C M, etc. Global existence and finite time blow-up for a degenerate reaction-diffusion system [J]. Basic Sciences Journal of Textile Universities, 2016,29(1):35-38. DOI:10.13338/j.issn.1006-8341.2016.01.006.

[5] 王文海.具非局部源和非局部边界条件抛物方程组解的性质[J].中北大学学报(自然科学版)，2012，33(4): 372-375. DOI:10.3969/j.issn.1673-3193.2012.04.005. WANG W H. Properties of solution to a parabolic system with nonlocal source and nonlocal boundary conditions[J].Journal of North University of China(Natural Science Edition) ，2012，33(4):372-375. DOI:10.3969/j.issn.1673-3193.2012.04.005.

[6] 樊彩虹,李平，郭晓霞，等.半线性反应扩散耦合系统解的整体存在与爆破[J].内蒙古师范大学学报(自然科学汉文版),2015,44(6):735-737,742. DOI:10.3969/j.issn.1001-8735.2015.06.004. FAN C H,LI P,GUO X X,et al.The Global existence and blow-up for the solutions of the system of semilinear reaction diffusion couling[J].Journal of Inner Mongolia Normal University(Natural Science tdition),2014,43(6): 680-688. DOI:10.3969/j.issn.1001-8735.2015.06.004.

[7] 王玉兰，穆春来.一类具有非局部源的拟线性抛物型方程组的一致爆破模式[J].四川大学学报(自然科学版)，2008，45(5):7001-3101. DOI:10.3969/j.issn.0490-6756.2008.05.002. WANG Y L, MU C L. Uniform blow up profiles for a quasilinear parabolic system with nonlocal sources[J].Journal of Sichuan University(Natural Science Edition), 2008，45(5):7001-3101. DOI:10.3969/j.issn.0490-6756.2008.05.002.

[8] 周泽文, 凌征球.源项耦合的退化抛物型方程组解的爆破和整体存在[J].应用数学，2015, 28(3): 540-548. ZHOU Z W, LING Z Q. Blow-up and global existence of solutions to a degenerate parabolic equations coupled via nonlinear sources[J]. Mathematica Applicata, 2015, 28(3): 540-548.

[9] 薛应珍.一类具有非线性吸收项和边界流的抛物型方程组解的整体存在及爆破问题[J].纺织高校基础科学学报，2013，26(2)：214-219. DOI:10.3969/j.issn.1006-8341.2013.02.017. XUE Y Z. Global existence and blow up problem for a parabolic equations with nonlinear absorption term and boundary flux[J]. Basic Sciences Journal of Textile Universities, 2013，26(2)：214-219. DOI:10.3969/j.issn.1006-8341.2013.02.017.

[10] 庞凤琴，王玉兰，李慧芳. 一类带吸引项的抛物型方程在记忆边界条件下解的性质[J]. 西华大学学报( 自然科学版),2016,35(2):82-87. DOI:10.3969/j.issn.1673-159X.2016.02.016. PANG F Q，WANG Y L，LI H F.The properties of a parabolic equation with absorb term and memoryboundary condition[J].Journal of Xihua University( Natural Science)2016,35(2):82-87. DOI:10.3969/j.issn.1673-159X.2016.02.016.

[11] ZHANG H，KONG L H, ZHANG S N. Propagations of singularities in a parabolic system with coupling nonlocal sources[J].Sci in China: Ser A，2009，52(1):181-194. DOI:10.1007/s11425-008-0135-7.

[12] LI Y X,DENG W B,XIE C H.Global existence and nonexistence for degenerate parabolic systems [J]. Proc Amer Math Soc,2002,130(12):3661-3670.

[13] DENG W B,LI Y X,XIE C H.Existence and nonexistence of global solution of some nonlocal degenerate parabolic system[J].Proc Amer Math Soc,2003,131(5):1573-1582. DOI:10.1016/s0893-9659(03)80118-0.

[14] ZHANG Y,SONG X J.Global existence and blow-up for a degenerate parabolic systems with nonlocal source [J].Journal of Southwest University(Natural Science Edition),2008,30(9):80-84.

[15] BUDDAL C J,DOLD J W,GALAKTIONOV V A.Global blow-up for a semilinear heat equation on a subspace [J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics,2015,145(5):893-923. DOI:10.1017/s0308210515000256.

[16] 党苏娟,容跃堂,张航国.非局部反应扩散方程组解的整体存在与爆破[J].纺织高校基础科学,2013,26(4): 481-485. DANG S J,RONG Y T,ZHANG H G.Global existence and blow-up of solution for nonlocal reaction diffusion equtions[J].Basic Sciences Journal of Textile Universities,2013,26(4):481-485.

[17] 樊彩虹,李平,郭晓霞，等.具非局部源退化抛物系统解的整体存在与爆破[J].内蒙古师范大学学报(自然科学汉文版),2014,43(6):680-688. FAN C H,LI P ,GUO X X,et al.Global existence and blow-up for the solutions of a degenerate parabolic system with nonlocal sources[J].Journal of Inner Mongolia Normal University(Natural Science Edition),2014,43(6): 680-688.

[18] 樊彩虹,容跃堂.一类带非局部源的反应扩散方程组解的整体存在[J].纺织高校基础科学学报,2009,22(2): 172-176. DOI:10.3969/j.issn.1006-8341.2009.02.011. FAN C H,RONG Y T.Global existence for a degenerate reaction-diffusion system with nonlocal sources[J]. Basic Sciences Journal of Textile Universities,2009,22(2):172-176. DOI:10.3969/j.issn.1006-8341.2009.02.011.

[19] ZHANG H，KONG L H, ZHENG S N.Propagations of singularities in a parabolic system with coupling nonlocal sources[J].Sci in China:Ser A，2009，52(1):181-194. DOI:10.3969/j.issn.1006-8341.2009.02.009.

[20] PAO C V. Nonlinear parabolic and elliptic equations[M].London:Plenum Press,1992.

(责任编辑：王兰英)

Global existence and blow up problem for a parabolic equations cross coupled terms

XUE Yingzhen

(College of Business, Xi'an International University, Xi'an 710077, China)

In order to better describe the heat transfer process of three kinds of mixed substances, or the reaction of the reactants in the three chemical reactions,a class of three variable cross coupling with non parabolic equations of the whole existence of local source and non local boundary flow and the finite time blow up problem with breaking method for the solution of the first commonly used feature value structure are studied, and the structure of the equations of the upper and lower solutions by using the method of ordinary differential equation reference, comparison theorem, the proof obtained by local source power function and exponential function of parabolic equations and the sufficient conditions for global existence of solutions blow up in finite time degradation of non local sources of cross coupling, provide better support for the theory of heat transfer and chemical reaction problem.

parabolic equations cross coupled terms; the comparison principle; global solution; blow up

10.3969/j.issn.1000-1565.2017.04.002

2017-02-21

陕西省自然科学基础研究计划项目(2016JM1036)；陕西省教育科学十三五规划课题(SGH16H292)

薛应珍(1980—)，男，甘肃庆阳人，西安外事学院副教授，主要从事偏微分方程理论及应用的研究. E-mail：xueyingzhen@126.com

O175.26

A

1000-1565(2017)04-0343-06