计算长度系数反推法在复杂结构中的应用
2017-09-01中冶京诚工程技术有限公司汪明国内贸易工程设计研究院崔芳中国建筑设计院有限公司伍敏
文|中冶京诚工程技术有限公司 汪明;国内贸易工程设计研究院 崔芳;中国建筑设计院有限公司 伍敏
1.引 言
随着人类社会的深入快速发展,人们在功能上和审美上均已不满足于传统的规则结构。近几十年间,大量功能复杂、形状不规则的公共建筑涌现在我们生活里。此类建筑结构形式灵活多变。在异型复杂结构的设计过程中,可参考的经验性通用方法较少,对结构计算的准确度要求较高。
结构稳定计算是复杂结构设计过程中的重要部分。以经典力学和稳定理论为基础的传统计算长度系数法是工程领域中被广泛应用和接受的一种方法。包括现行《钢结构设计规范》在内的大量经典钢结构设计文献均推荐了该稳定计算方法。在稳定验算中涉及两个关键参数:计算长度系数(μ)和构件受压稳定系数(φ),以考虑结构和构件的自身缺陷和二阶效应对构件稳定承载力的影响。基于大量相关试验和理论的研究,在《钢结构设计规范》(GB50017-2003)等文献中给出了如框架柱(有侧移框架和无侧移框架)、排架柱等规则结构竖向构件的计算长度系数。但由于计算长度系数与构件边界约束条件、相邻结构刚度等诸多因素有关,因此对于大部分异型复杂结构,并不能通过主观经验性判断或简单计算而准确地确定构件计算长度系数。
本文将概要介绍一种以屈曲分析结果为基础反推受压或压弯杆件计算长度系数的方法。并通过具体工程实例,介绍该方法在异型结构中的应用过程。另外,通过与直接分析法的计算结果进行比较,验证该方法的准确性。
2.计算长度系数反推法概述
在不考虑材料塑性情况下,理想受压杆件的屈曲临界压力可通过对杆件受力状态微分方程求解得到。图1所示是典型理想受压杆件受力和变形简图。
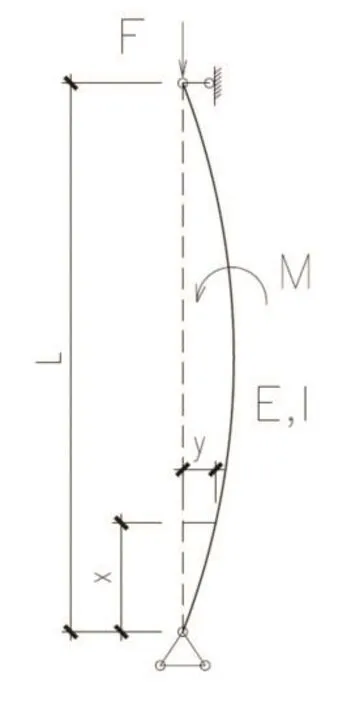
图1 理想受压杆件简图
在几何失稳状态时(F=Fcr),杆件内任一截面处的弯矩满足以下方程:

杆件翘曲线近似微分方程:
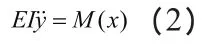
其中,E是弹性模量;I是截面转动惯性矩。
通过式(1)和式(2)合并可建立微分方程,如下:

求解该微分方程,最终可得到欧拉临界力:

另外,可确定杆件变形曲线为:
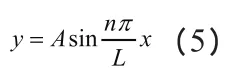
式中,n为杆件变形曲线半波数;A为杆件侧向变形最大值。
将欧拉临界力公式(式(4))变形得到下式:
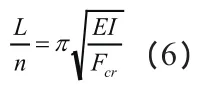
L/n为杆件计算长度,即为变形曲线的半波长度。计算长度系数μ=1/n,则
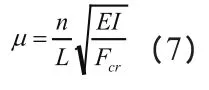
对于边界约束简单的构件,可轻易确定变形半波长度,若两端铰接,则半波长度为L,即计算长度系数为1.0;若两端刚接,则半波长度为0.5L,则计算长度系数为0.5。但对于实际结构中的大部分杆件,边界约束情况复杂,无法轻易确定屈曲变形半波长度,即无法确定计算长度系数。

图2 主结构三维轴测图

图3 主结构平面布置图

图4 短向剖面图
然而,借助通用结构计算软件可实现对复杂结构的屈曲分析,从而得到主要受力杆件的临界压力值,即得到式(7)中的Fcr,从而可间接计算得到计算长度系数μ。
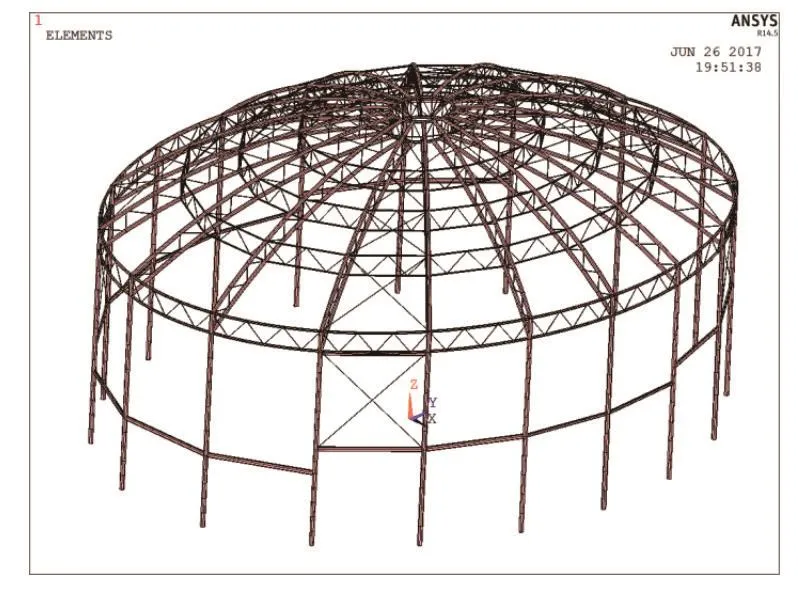
图5 有限元计算模型
3 工程应用
下文将介绍计算长度系数反推法在某异型结构中的应用。本工程为一座大型表演剧场,主体结构为64×80m的椭圆穹顶结构,结构形式如图2-图4所示。
该结构为椭圆穹顶结构,由五道环向桁架、18榀径向桁架、4道屋面支撑、18根钢柱组成。在竖向力作用下,该结构可实现水平力自平衡,即柱底产生的水平推力较小。
整个结构由膜材覆盖。考屋面恒荷载为0.3kN/m2;雪荷载为0.5 kN/m2;吊挂荷载为0.3 kN/m2;基本风压为0.45 kN/m2。
18根钢柱截面为圆管520×18。底部与基础刚接,顶部双向分别与环桁架、径向桁架连接。若采用《钢结构设计规范》(GB50017-2003)进行钢柱稳定承载力验算,则首先应确定钢柱的计算长度系数,但现有规范仅给出了如框架柱、排架柱等典型结构形式中柱子的计算长度计算方法。对于此类结构,并不能通过简单判断确定柱子计算长度系数。
下文将介绍计算长度系数反推法在本工程中的应用过程。采用有限元通用分析软件ANSYS建立该结构模型,如图5。
由于该分析目的为确定钢柱计算长度系数,为了避免其它构件屈曲模态对结果的影响,在计算模型中仅在所有钢柱顶部施加1kN竖向作用力。在该基本荷载条件下,进行线性屈曲分析,得到结构屈曲特征荷载如表1。第一屈曲模态见图6。
由于舞台区钢柱间无法设置环梁,因此,此区域内钢柱刚度较弱。从第一屈曲模态看,可见舞台区钢柱先发生屈曲,所对应屈曲临界荷载为5839kN。
根据计算长度系数反推公式:
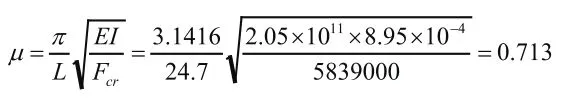
因此,舞台区钢柱计算长度系数可取0.713,由于其它区域钢柱临界荷载略高,理论上其计算长度系数应略小于0.713。
4 通过直接分析法验证
根据《钢结构设计规范》(GB50017-2003)中受压杆件的验算方法,该钢柱轴心受压承载力设计值为:

按照上文得到的计算长度系数为0.713考虑,该柱子长细比为:
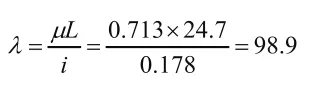
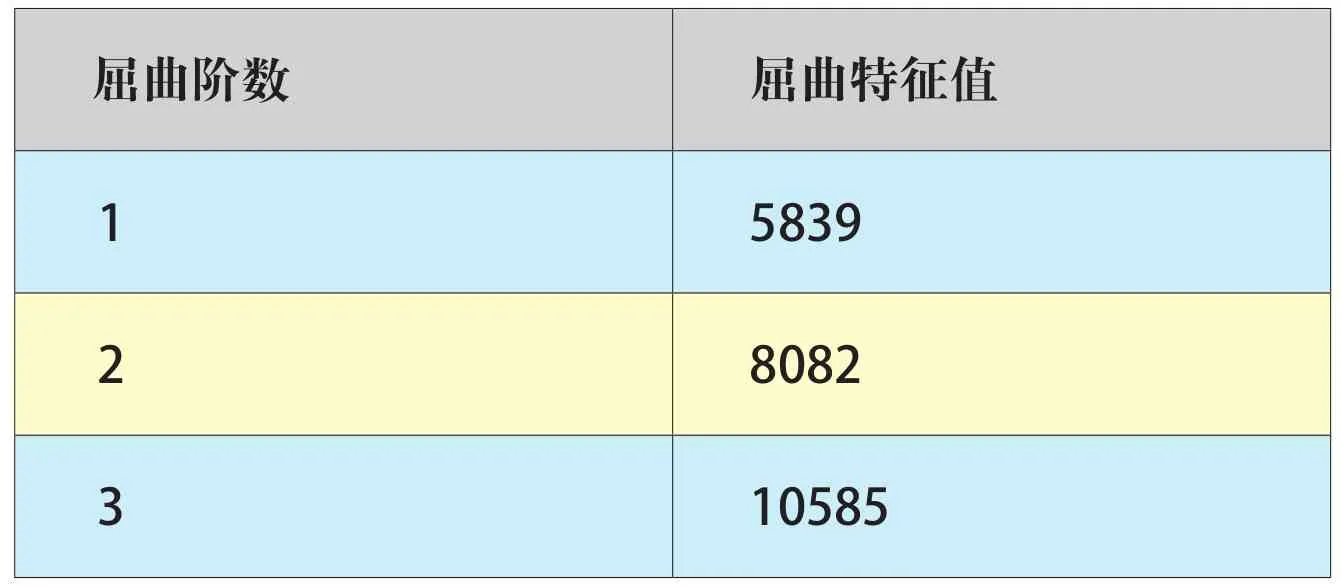
表1 前3阶屈曲特征值
查《钢结构设计规范》(GB50017-2003)附录C(按a类截面,考虑钢号折减),得到稳定系数,因此,钢柱受压承载力设计值为:
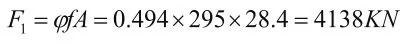
为了验算上述方法的准确性,下文将采用计算精度更高的直接分析法进行验证。与传统计算方法不同,采用直接分析法的计算模型需考虑结构和构件的初始缺陷。
按照柱子高度1/250考虑整体结构初始缺陷,缺陷形态为第一阶屈曲模态,考虑整体缺陷后的结构模型如图7。
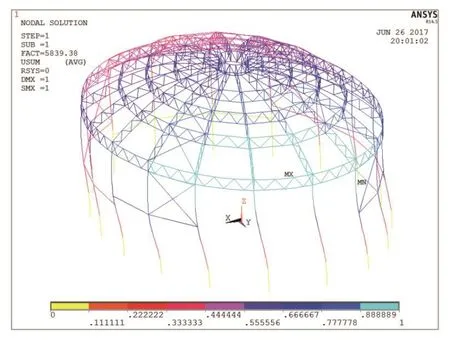
图6 第一阶屈曲模态
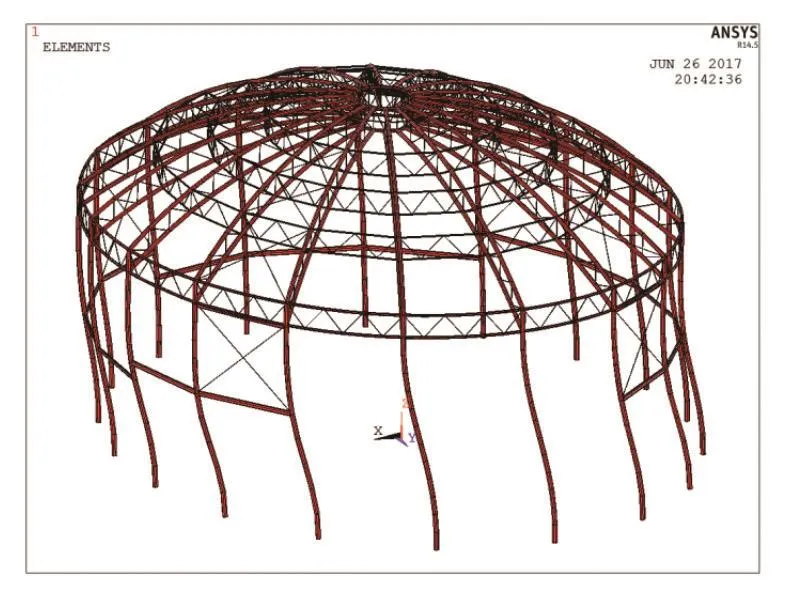
图7 考虑结构整体缺陷后的模型(已放大20倍呈现)
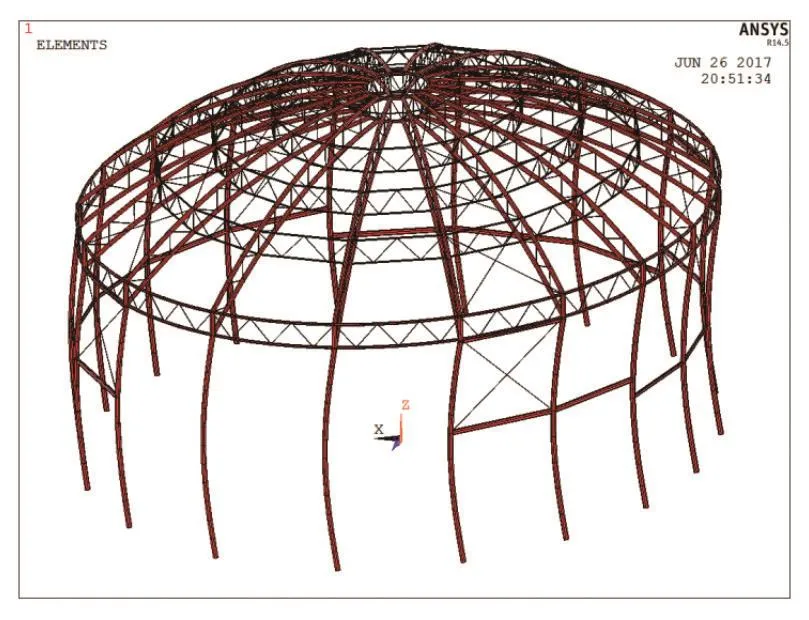
图8 考虑构件缺陷后的模型(已放大20倍呈现)
柱子自身缺陷按照高度1/400考虑,缺陷形态为正弦半波曲线,考虑构件初始缺陷后的结构模型如图8。
综合考虑上述两种不同缺陷,重新建立有限元模型,同样仅在所有钢柱柱头施加竖向荷载,采用弧长法进行非线性计算(同时考虑材料非线性和几何非线性),得到柱头节点竖向位移和作用力(设计值)之间的历程关系曲线,如图9。

图9 直接分析法荷载位移历程曲线
图9曲线表明通过直接分析法得到钢柱的最大竖向承载力设计值F2为4196kN,略高于计算长度系数反推法得到的柱子承载力设计值F1,误差率γ为:
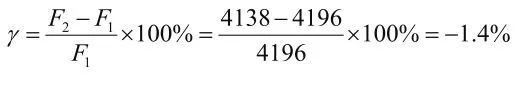
上述对比结果表明:通过屈曲临界荷载反推得到计算长度系数,并将该系数应用于传统一阶弹性稳定计算法中得到的柱子受压承载力设计值基本与采用直接分析法计算得到的受压承载力设计值相符。
5 结论
本文阐述了一种基于线性屈曲临界荷载反推受压杆件计算长度系数的方法。并通过工程实际,介绍了该方法在异型复杂结构中的应用。另外,通过与直接分析法进行比较,验证了该方法的准确性。此方法对计算异型结构中边界约束情况较复杂的受压杆件的计算长度系数具有指导意义。
