随机系统稳态概率密度函数控制算法

杨恒占，张晓倩，毕雪琴

(西安工业大学 电子信息工程学院，陕西 西安 710021)

随机系统稳态概率密度函数控制算法

杨恒占，张晓倩，毕雪琴

(西安工业大学 电子信息工程学院，陕西 西安 710021)

对于非线性随机系统，以均值、方差为控制目标的传统控制方法难以达到满意的控制效果，而概率密度函数控制能够反映非线性随机系统的各阶统计特征，可实现较为理想的控制效果。为此，针对非线性随机系统，提出了一种对系统状态稳态响应的概率密度函数进行控制的算法。该算法将概率密度函数展开为多项式形式，以FPK方程为工具，分析并得出多项式系数和控制多项式增益的关系方程组，以该方程组的解为控制增益的函数，通过进一步构造一个优化问题来解决该方程组存在的超定问题。根据目标概率密度函数的要求，确定出控制多项式的各项增益，给出并实现该算法的计算机实施步骤。仿真结果表明，所提出的算法有效可行，可离线计算且计算效率较高，能够实现概率密度函数的良好控制。

随机系统；概率密度函数；多项式；非线性

1 概 述

随机控制的基本理念就是处理系统中的不确定性，通过对被控对象施加特定的输入信号，驱动被控系统朝着期望的目标运行。随着计算机技术的快速发展，随机控制理论也得到了深入研究与应用。由于在随机环境下对系统进行分析非常困难，因此，对于具有特殊结构的动态系统，以均值、方差等低阶统计特征为目标的分析与调节方法得到了深入研究和快速发展[1]。这些方法大都以某个目标函数的最优化为出发点，能够有效解决线性系统的控制问题，典型代表如最小方差控制[2]、线性二次型高斯控制理论[3-6]。

对于确定性系统来说，状态是系统历史行为的总结，包含过往施加于系统的控制和系统所处的初始状态，完全刻画了系统的全部行为。而对于随机系统来说，即使系统能够准确地从同一个初始状态出发，并且在每个时刻用完全精确的同一控制律进行控制，由于测量和状态受到随机扰动，系统每次运行到同样时刻的状态仍然各不相同，状态以概率转移的方式运作。因此，与确定性情况下的状态不同，随机情况下的状态对系统行为的描述是不完全的。而概率密度函数则包含了系统的动态信息、扰动信息，尤其是非线性的所有统计特征信息。

一旦概率密度函数确定下来，传统方法中的均值、方差等低阶统计特征信息都能够很容易地计算出来。而且，概率密度函数相比传统的均值、方差等低阶统计特征包含了更多的系统过程信息，更能揭示出随机系统运行过程中的丰富信息。例如控制过程中经常需要确定系统动态过程结束后的稳态情况，就对应于概率密度函数的末端形状。在传统以均值、方差为指标的方法中，这些信息都无法顾及到，从而出现信息丢失情况，只有高斯对称形状的概率密度函数才可以使用随机变量的低阶统计特征来度量。线性随机系统之所以使用传统方法控制就能取得良好效果，原因就在于系统状态的概率密度函数是高斯型形状，除了均值和方差外，其余高阶统计特征都无实际意义。

而对于非线性系统，其性能指标除了均值、方差外，还需要顾及更高阶的统计特征，例如峭度、陡度等。在控制指标上，某些工业生产过程常常以安全、质量、环保等为控制指标。这些指标往往不需要达到最优，只需要约束在某个允许的范围内。这类控制问题使用概率密度函数形状作为控制目标就更为合适，控制器设计的目的是让系统在要求的指标范围内运行[7]。在这种情况下，以完全统计特征为目的的分析与控制方法在近年来应运而生，受到越来越多的重视[8-10]。概率密度函数控制方法是对随机过程统计特征的完整刻画，远远优于以低阶矩近似的统计量的控制方法，也因此表现出了优秀的控制性能和研究价值[11-14]。

针对非线性随机系统，为克服FPK方程求解的固有难题，在分析概率密度函数跟踪问题的基础上，提出了一种对系统状态稳态响应的概率密度函数进行控制的算法。该算法通过将概率密度函数展开为多项式，以FPK方程组为工具，成功推导出稳态概率密度函数和随机系统的关系，将方程组的解为控制增益的函数。同时，为使被控概率密度函数形状具有期望的形式，构造了一个优化问题，并搜索出了最优控制增益，实现了概率密度函数的良好跟踪。

2 问题描述

考虑处于随机环境中的如下标量非线性系统：

(1)

其中，z(t)∈为系统状态；z0为初始状态；w(t)∈为高斯白噪声，其均值为零，谱密度为S0；φ(·)∈为非线性函数，表示系统模型。

假定φ(z)为如下多项式形式：

φ(z)=α0+α1z+α2z2+…+αmzm

其中，m为多项式阶数。

如果φ(z)不具备多项式形式，可以将φ(z)关于z进行Taylor级数展开，用Taylor级数展开的前m+1项逼近φ(z)。

希望确定一个状态反馈函数μ(t)=u(z)，在该函数的控制下，z(t)到达稳态时对应的概率密度函数ρ(z)能够跟踪期望的形状ρd(z)。

一般来说，非线性系统的控制需要使用非线性控制律，如果使用线性控制律则很难达到控制目的。因此，采用的u(z)形式如下：

u(z)=β0+β1z+β2z2+…+βnzn

其中，n为多项式阶数。

因此，问题描述如下：

确定u(z)的参数β0,β1,…,βn，使系统

(2)

稳态时对应的概率密度函数ρ(z)能够跟踪期望的形状ρd(z)。其中h(z)=φ(z)+u(z)=b0+b1z+b2z2+…+bxzx。bi和αi、βi关系如下：

(3)

其中，x取值为max(m,n)。显然，如果m较大，则βn+1到βm都为0；如果n较大，那么αm+1到αn则都为0。

3 多项式展开概率密度函数控制方法

系统(2)对应的FPK方程为[15]：

(4)

其中，D=πS0。

假设FPK方程具有如下v次多项式形式的近似解：

(5)

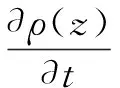
(6)

因为ρv(z)仅为方程(4)的近似解，也即为方程(6)的近似解。这样，将式(5)直接代入方程(6)不会使得该方程成立。不过，可以采用如下方法确定待定的常数si。

首先固定常数v，然后将式(5)代入式(6)的左边，则有：

(7)

求解y(z)的具体形式，有：

R{[(s0b1+s1b0)+2(s0b2+s1b1+s2b0)z+…+

(v+x)svbxzv+x-1]+D[2s0+6s3z+…+

v(v-1)zv-2]}=R[(s0b1+s1b0+2Ds0)+

2(s0b2+s1b1+s2b0+3Ds3)z+…+

(v+x)svbxzv+x-1]=R[c0+2c1z+…+

(v+x)cv+x-1zv+x-1]

(8)

可见，y(z)也具有多项式形式。如果ρv(z)是方程(6)的精确解，则y(z)=0。如果ρv(z)不是方程(6)的精确解，则y(z)≠0，此时y(z)可以认为是用近似解ρv(z)代替精确解ρ(z)所引起的误差。该误差越小，ρv(z)越精确。为使误差尽可能小，令y(z)多项式各阶系数c0,c1,…,cv+x-1都为0，得到如下线性方程组：

(9)

可见，随机系统(2)中多项式h(z)的各项系数b0,b1,…,bx和该系统的稳态概率密度函数ρ(z)的多项式形式的各项系数s0,s1,…,sv之间存在式(9)所蕴含的关系。如果h(z)形式已知，解该方程组，可以求出s0,s1,…,sv，进而得到随机系统(2)的稳态概率密度函数ρ(z)。

反之，如果ρ(z)已知，解该方程组，则可以求出b0,b1,…,bx，进而通过式(10)得到β0,β1,…,βn的值，从而确定出控制器u(z)的具体形式：

(10)

研究目的为根据期望的密度函数ρd(z)来确定控制器u(z)的结构形式。结合该方法，s0,s1,…,sv可由ρd(z)求出，代入方程组(9)，求出b0,b1,…,bx，就可以实现研究的目的。

遗憾的是，一般情况下，方程组(9)中的方程个数都超过了变量b0,b1,…,bx的个数，即出现超定现象，导致方程组的求解出现困难，甚至解不存在。

为解决上述超定问题，构造如下优化问题：

(11)

(12)

通过该方法，能够确定出u(z)的参数，使得在u(z)的作用下，系统(2)稳态时对应的概率密度函数ρ(z)能够跟踪期望的概率密度函数ρd(z)，从而达到研究目的。

4 仿真分析

综合上述分析，随机系统概率密度函数算法的计算机实现步骤如下：

Step1：约束ρd(z)具备多项式展开形式，指定多项式最高次数为x；

Step3：判断e是否满足精度要求。如果满足要求进入Step4，否则增大x的值并返回Step2；

Step4：按照式(10)计算βi的值；

Step5：根据式(12)确定控制器u(z)的结构。

下面给出实例仿真。

考虑如下白噪声激励的非线性系统：

(13)

其中，w(t)是均值为0的高斯白噪声，其谱密度为1/π。

期望的概率密度函数为：

(14)

ρe(z)形状上是一个半圆。容易得到其θe0,θe1,…,θen分别为：θe0=0.798，θe1=0，θe2=-1.253，θe3=0，θe4=-5.906，θe5=0

取u(z)最高阶数和φ(z)最高阶数一致,按照所提出的方法，调节后的概率密度函数为：

(15)

对应的调节函数为：

u(z)=-0.941z+0.182z2+2.392z3

(16)

用u(z)调节目标系统，状态z稳态时的概率密度函数的形状如图1所示。可见，调节后的概率密度函数对目标概率密度函数跟踪较好。

图1 u(z)控制下的概率密度函数

5 结束语

针对非线性随机系统，通过对概率密度函数展开为多项式的方法，以FPK方程为工具得到了控制增益和概率密度函数多项式系统的关系，并进一步实现了概率密度函数的良好控制。针对普通的非线性随机系统，通过把概率密度函数表述为多项式方式，一般能够解决概率密度函数的控制问题，线性方程组计算尽管存在超定问题，但通过优化问题计算起来也比较简单。从仿真实例可以发现，针对一般的非线性随机系统，该算法达到了理想的控制效果。但若被控概率密度函数过于复杂，可能出现解出的概率密度函数出现负值的情况，会影响系统的控制效果。这个问题是后续进一步研究解决的重点。

[1] 郭尚来.随机系统[M].北京:清华大学出版社,1999.

[2] Guo X Y,Li J M. Stochastic adaptive synchronization for time-varying complex delayed dynamical networks with heterogeneous nodes[J].Applied Mathematics and Computation，2013,222(5):381-390.

[3] Li D,Qian F C,Gao J J.Performance-first control for discrete-time LQG problems[J].IEEE Transactions on Automatic Control,2009,54(9):2225-2230.

[4] 钱富才,李 江,赵 平.双重不确定性系统的跟踪与辨识[J].系统工程理论与实践,2012,32(4):839-846.

[5] Qian F C,Gao J J,Li D.Complete statistical characterization of discrete-time LQG and cumulant control[J].IEEE Transactions on Automatic Control,2012,57(8):2110-2115.

[6] Yue H,Wang H.Minimum entropy control of closed-loop tracking errors for dynamic stochastic systems[J].IEEE Transactions on Automatic Control,2003,48(1):118-122.

[7] Yang H Z,Qian F C,Gao S,et al.The shape control of probability density function for a class of stochastic systems[J].System s Engineering - Theory & Practice,2016,36(9):2424-2431.

[8] 姜文涛,刘万军,袁 姮.基于软特征理论的目标跟踪研究[J].计算机学报,2016,39(7):1334-1355.

[9] Amineh A,Teh Y W,Hadi S.On density-based data streams clustering algorithms:a survey[J].Journal of Computer Science & Technology,2014,29(1):116-141.

[10] 王法胜,鲁明羽,赵清杰,等.粒子滤波算法[J].计算机学报,2014,37(8):1679-1694.

[11] 杨恒占,钱富才,黄姣茹,等.一类随机系统完全统计特征控制[J].控制理论与应用,2016,33(5):669-675.

[12] 栾小丽,刘 飞.随机系统输出概率密度函数的有限时间镇定[J].控制与决策,2009,24(8):1161-1166.

[13] Guo L,Wang H.Stochastic distribution control system design[M].London:Springer,2010.

[14] 黄锦旺,李广明,冯久超,等.一种无线传感器网络中的混沌信号重构算法[J].物理学报,2014,63(14):77-83.

[15] Wagner U V,Wedig W V.On the calculation of stationary solutions of multi-dimensional Fokker-Planck equations by orthogonal functions[J].Nonlinear Dynamics,2000,21(3):289-306.

Dual Control Algorithm for Stochastic System with Parameters Drifting

YANG Heng-zhan，ZHANG Xiao-qian，BI Xue-qin

(School of Electronic and Information Engineering,Xi’an Technological University,Xi’an 710021,China)

For nonlinear stochastic systems，the traditional control methods with the mean or variance as control target are difficult to achieve good control effect.The probability density function could express the complete characterization of the system,therefore it can reach an ideal performance.A novel algorithm of probability density function control is proposed for the nonlinear stochastic systems in the stationary case.The relationship between steady-state probability density function and stochastic system is successfully deduced with the method of expanding the probability density function into polynomial according to the FPK equations.An optimization problem is further constructed to solve the over-determined problem of the equations.Thus the gain control of polynomials is calculated according to the requirements of the target probability density function.Its computer implementation steps are given eventually.Simulation illustrates it is effective and feasible,which can be offline computation wwith high efficiency and good control effect.

stochastic system;probability density function;polynomial;nonlinear

2016-11-01

2017-02-21 网络出版时间：2017-07-05

陕西省教育专项科研计划项目(16JK1364)

杨恒占(1976-)，男，讲师，硕士，研究方向为嵌入式系统、随机控制、最优控制。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1653.090.html

TP301.6

A

1673-629X(2017)08-0102-04

10.3969/j.issn.1673-629X.2017.08.021