基于复杂网络理论的粮食供应链网络抗毁性研究
2017-08-31王登清
王登清
(福州大学经济与管理学院, 福建福州 350116; 福建船政交通职业学院, 福建福州 350007)
基于复杂网络理论的粮食供应链网络抗毁性研究
王登清
(福州大学经济与管理学院, 福建福州 350116; 福建船政交通职业学院, 福建福州 350007)
从粮食供应链网络的信息流、物流、商流等维度提出粮食供应链网络构建模型,并针对粮食供应链网络的特点提出两个抗毁性测度指标即网络安全性和网络平均效率指标。该网络抗毁性测度可较好地描述网络抗毁性能的变化特性。利用粮食供应链网络抗毁性仿真实验发现:粮食供应链网络点随机攻击要比边随机攻击对网络安全的影响大;粮食供应链网络的蓄意攻击表现脆弱,而对随机攻击具有鲁棒性;粮食供应链网络抗毁性是由少数重要节点和边进行支撑的,因此应加强重要节点和边的保护力度,以提高网络的整体抗毁性。
复杂网络; 粮食供应链; 网络抗毁性; 介数
引言
我国是农业大国,人口众多,粮食的供应问题不仅关系到广大农民的切身利益,而且与城乡居民的生活供给和生命保障休戚相关。建立高效、安全、稳定的粮食供应体系是关系到国计民生的大问题。建国60多年来我国粮食供应取得了长足的进展,十三五期间集中新建仓容1000亿斤,应急供应网点达到5万家,应急加工企业达到0.6万家,改建成品粮批发市场312家,改建区域性配送中心531个。国内现有的粮食供应体系在节点布局、网络设计、运作模式选择等方面均存在不足,导致粮食供应领域流通成本高、物流效率低、服务水平差等问题突出。在农产品供应体系中,供应链网络的结构与网络性能存在直接的关系,粮食交易关系中断、自然灾害或交通事故导致的粮食物流网络的破坏会改变现有粮食供应网络的结构,从而影响到粮食的配送成本和配送效率。因此,研究粮食供应网络可能遭受的破坏,分析网络破坏后对粮食供应的影响,对于做好突发事件下粮食供应的应急预案,制定有效的粮食供应网络保障策略具有重要意义。
粮食供应体系的安全保障问题,一直都是农产品相关领域研究的焦点,相关文献较多。冷志杰等人通过农产品供应链的水平结构、垂直结构、核心企业位置和产品的种类四个维度分析供应链结构,构建有效农产品供应链。[1]学者利用复杂网络理论,探索复杂网络的演变规律、结构功能和动力学行为。特别是近年许多研究者开始关注网络抗毁性能的测度研究,建立了连通度、聚集度和最短平均路径距离等网络性能测度模型。[2][3][4]陈春霞基于复杂网络理论,引入平均最短路径距离和极大连通子图,在最大度和介数等不同的攻击策略下分析了单点应急物流网络的抗毁性能。[5]种鹏云引入危险品运输网络“最短路径”、“平均最小风险路径距离”和“网络最大连通子图”概念,提出了“网络风险效率”和“最大连通度”抗毁性侧度模型。[6]学者从供应链网络抗毁性角度进行了研究,但较少在粮食供应链网络领域进行抗毁性研究。由于粮食供应链网络自身具有动态性等特点,仅从静态的角度研究抗毁性具有一定的局限性。
一、问题的提出
粮食供应链网络是从粮食的供应地、消费地转移过程中由众多的农户、粮食厂商、粮食经销商、粮食消费者、物流服务商所组成的整体网链式结构。粮食供应链网络是由物流、商流、信息和资金等众多网络交织形成的复杂网络。Nagureny等在研究供应链网络问题时首次提出“超网络”的概念,用来描述那些高于而又超于现存网络的网络。[7]
粮食供应链网络是由粮食仓库、物流中心以及将它们连接在一起的物流线路所组成的一个物流运输网络,这表明了粮食供应链网络的物理层特征;粮食供应链网络也是由众多的粮食农户、粮食厂商和粮食经销商所组成的商业交易网点网络,上游粮商根据下游客户的需求状况进行粮食的配送,这表明了粮食供应链网络的业务层特征;当粮食供应链网络的某些节点或边遭受到随机或蓄意攻击而失效,会间接影响粮食供应链网络功能的发挥,这表明粮食供应链网络的管理特征,因此,粮食供应链网络是一种典型的超网络。
粮食供应链网络具有多维视角、多层次性、多流性、动态性、风险性等特点。[8]从单一角度很难全面描述供应链网络结构特征,需借助复杂网络理论的某些模型参数对供应链网络进行量化描述。
二、三维度的粮食供应网络模型
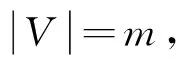
这样便将粮食供应链网络转换成一个包含农户、粮食厂商、分销商、物流中心、消费者和物流线路的赋权无向相连通图,通过随机和蓄意攻击该赋权无向连通图的节点和边来研究粮食供应链网络的安全性能。
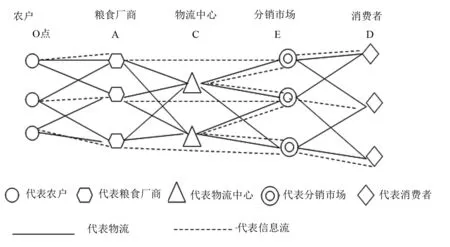
图1 粮食供应链网络模型
三、粮食供应链网络的抗毁性测度指标
网络遭受破坏时,其结构和通过性能均将发生改变。目前,在复杂网络研究领域,一般用网络直径、平均最短路径长度、网络效率和最大连通子图等测度指标来衡量网络的抗毁性能。就现实的粮食供应链网络而言,网络的安全性能和网络的平均效率是反映其抗毁性特征的两大重要指标。安全性能,反映的是当农产品供应网络遭受破坏时,是否能保证粮食供应的安全性,即粮食供应是否会因为破坏行为而中断,网络OD之间的连通性是否受破坏影响;网络的平均效率则是指粮食供应网络遭受破坏后,从供应方到需求方的粮食供应效率或供应成本改变情况。网络安全性和网络平均效率指标定义为:网络安全性指标、网络的损失度及网络平均效率指标。
(一)网络安全性指标
粮食供应的安全性是粮食供应链网络设计和运营过程中应考虑的首要因素。复杂网络理论通常运用网络平均最短路径指标来表示网络的脆弱性特征,并将网络中任意两个节点之间的最短路径的平均值称为平均最小风险路径(式(1))。
L(G)=﹤d(i,j)﹥
式(1)中,n为粮食供应链网络中的节点数目。平均最小风险路径L(G)体现了粮食供应链网络在遭受破坏时网络连通性的变化情况。平均最小风险路径越小,说明网络节点之间的连通性越好,网络的风险值越小。粮食供应链网络遭受破坏,网络或者网络边可能出现失效的情形,网络连通性将会受到影响。随着破坏的进行,网络将会被分解成为若干个子图,甚至出现孤立节点,连通性彻底破坏。此时,节点之间的平均最短路径的距离d(i,j)=+。为了便于描述网络彻底破坏的情形,将节点之间的平均最短路径值的倒数之和的平均值称为网络安全效率指标。
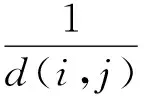
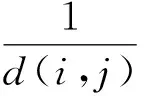
复杂网络理论通常应用节点删除法、边删除法来模拟对网络节点和网络连接边的破坏。本文也考虑基于节点(边)删除的破坏方法,在上述网络平均最小风险路径值指标L(G)和网络效率指标E(G)的基础上,定义粮食网络安全性指标如下:
定义1 运用节点删除法模拟网络破坏时,若删除第n个节点使得网络中出现d(i,j)=+的情形,则定义删除节点个数n占网络节点总数的N比例μp为基于节点破坏的粮食供应链网络安全临界值,即μp=
定义2 运用边删除法模拟网络破坏时,若删除第m条边使得网络中出现d(i,j)=+的情形,则定义删除边的条数m占网络边总数的M比例μe为基于边破坏的粮食供应链网络安全临界值,即μe=
(二)网络的损失度及网络平均效率指标
粮食供应链网络不仅具有特定的网络结构,同时网络上还有动态的粮食流。当粮食供应链网络遭受破坏时,随着网络拓扑结构的变化,粮食流的配送路径将发生相应变化,粮食配送的效率和配送成本也将发生相应改变。因此,仅仅研究静态网络结构的变化,无法准确描述粮食供应链网络遭受破坏以及破坏产生后的损失情况。在研究粮食供应链网络的整体抗毁性能时,需要考虑供应链网络上粮食流的流量和流向变化。本文将考虑多种破坏模式下粮食供应链网络的抗毁性能,探讨实施于粮食供应链网络上的破坏对网络结构和网络流的影响。将粮食供应链网络的广义损失测度指标定义为:
式(3)中,D=(dij)m×n表示网络节点之间的最短距离,G=(gij)m×n表示网络节点之间的粮食流量,且任意两个节点vi、vj之间的广义损失测度指标值可以表示为:Lij=dij×gij。在网络中任意两节点vi、vj之间的粮食流量gij保持不变的情况下,粮食供应链网络遭受破坏时,由于网络结构的变化,vi、vj之间的距离dij将发生变化(增大),因此,粮食供应链上的物流成本dij×gij将增大,即网络破坏将使得粮食供应链上的损失增大。为了更好地描述粮食供应链网络的抗毁性能,将网络中任意两点之间物流成本损失平均值定义为供应链网络的平均效率,如公式(4)所示。用该效率值来衡量网络的抗毁性能。
四、粮食供应链网络的破坏模拟
复杂网络理论通常采用节点删除和边删除的方法来模拟对网络的破坏,另外,从破坏的性质来看,也有两类即随机破坏和蓄意破坏。随机破坏即完全随机地删除网络中的一定比例节点或边;蓄意攻击,即总是按照节点或边的重要度排序开始,然后依次删除一定比例节点和边。现实的粮食供应链网络可能因交通事故、恶劣天气等随机发生的事故而遭受破坏,也可能遭受恐怖分子的蓄意攻击。
在蓄意破坏的模式下,被选择的攻击目标通常是网络中的重要节点或者关键边,这些节点(或者边)遭受攻击破坏后将造成巨大损失。复杂网络理论通常采用度值、介数值、接近度值等指标来衡量网络节点(或者边)的重要性。因此,在模拟蓄意破坏的过程中,节点按照度值或介数值大小排序,并按照顺序进行破坏。度值是指节点与周边节点的连接关系,反映节点的中心性特征,并不一定能反映节点的重要程度,因为它忽视了网络的流量和负载。图论中网络的介数值反映了相应的顶点或者边在整个网络中的作用和影响力,能反映节点的枢纽特征。因此本文拟采用基于介数的攻击策略来研究供应链网络的抗毁性。
在复杂网络理论中,介数是对经过某个节点最短路径数目的一个统计量。记网络节点和边的介数分别为Bv(V)和Bv(e),则介数定义为:
其中,σij(V)表示节点i和j之间所有最短路径中经过节点V的数量m,σij为节点i和j之间所有最短路径的数量;σij(e)表示节点i和j之间所有最短路径中经过边e的数量。
在实际粮食供应链网络中,网络中的每条物流路径和节点通过的最大物流量互不相同。如果攻击网络节点负载流量大的边或节点造成的危害要远远大于负载流量小的边或节点,采用公式(5)和 (6)去表征供应链网络的抗毁性,可能会和实际情况不相符。本文考虑网络中的流量因素,将供应链网络的介数重新定义为:
其中,Bvnew(V)为供应链网络G中节点V的介数,ξij(V)为节点i和j之间所有最短路径中经过节点V的所有路径的流量之和,ξij为节点i和j之间所有最短路径的总负载流量;Bvnew(e)为供应链网络G中边e的介数,ξij(e)为节点i和j之间所有最短路径中经过边e的所有路径的流量之和。
五、仿真算例
现假设2个物流中心、8个粮食供应点、12个粮食分销点和需求点及49条边组成粮食供应链网络,根据前文提出的粮食供应链网络生成方式,将供应链网络抽象成V=22,E=49的赋权无向相连通图(如图2)。利用粮食供应链网络的抗毁性侧度模型指标,在网络不同攻击策略下进行仿真计算,测算网络抗毁性。本文在仿真试验中,随机攻击策略采用每次删除一个节点,并连续进行5次取平均值;蓄意攻击策略按照节点和边介数的大小顺序进行删除,当遇到多个相同的节点和边时,随机选取其中的一个。
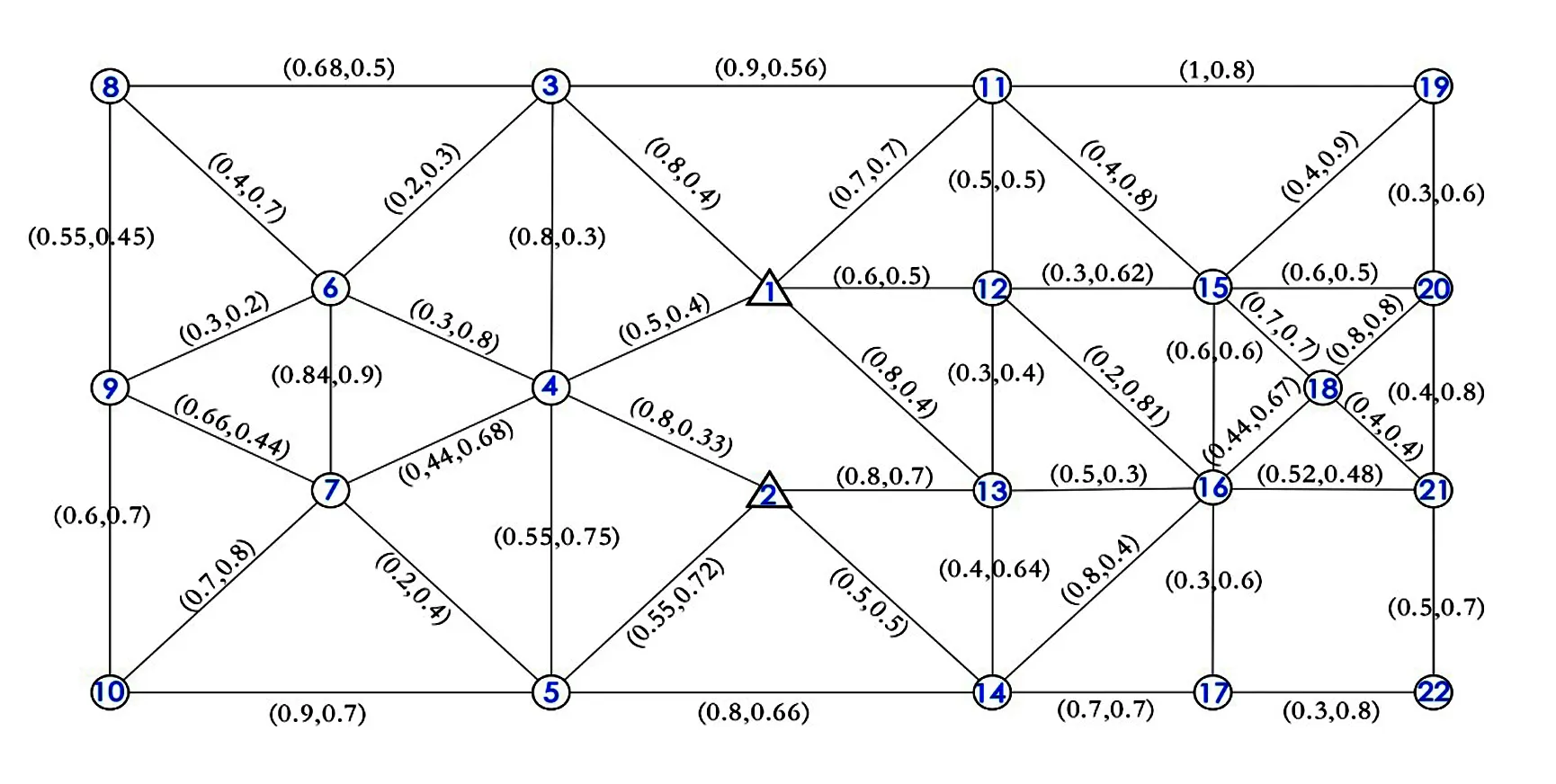
图2 粮食供应链网络仿真
(一 )节点删除破坏模拟及网络安全评价
运用节点删除法模拟外部对粮食供应链网络节点的攻击。分别运用随机删除节点和基于介数值大小排序的删除方法,模拟随机破坏和蓄意攻击。运用网络安全效率的参数值E(G)描述粮食供应链网络在遭受破坏时的网络安全状况,并对两种破坏方式作用下粮食供应链网络安全状况变化情况进行描述(如图3)。
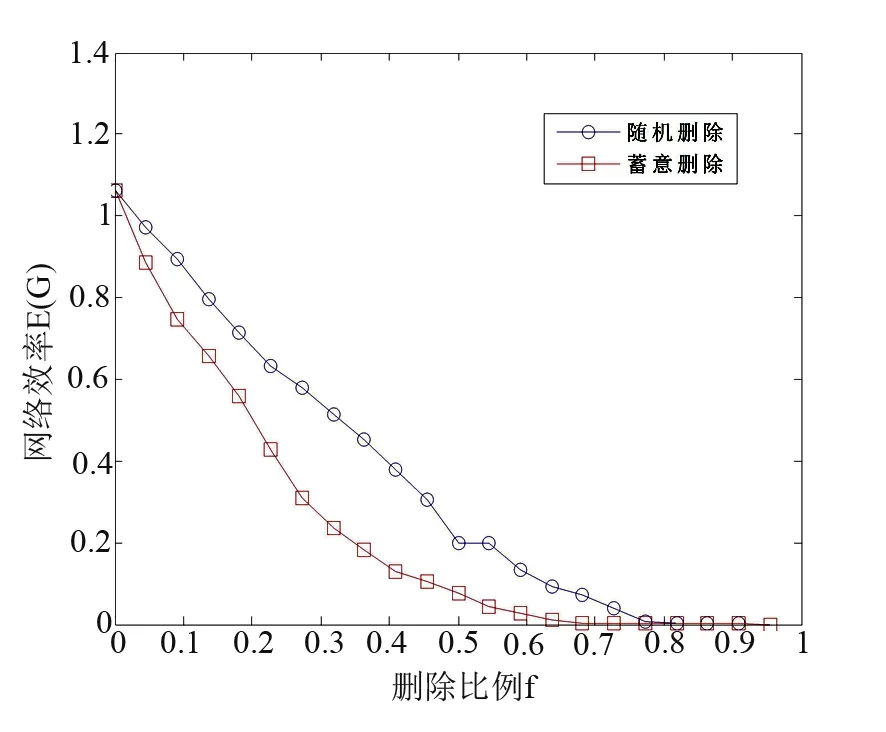
图3 随机和蓄意删除节点对比分析——以网络安全效率E(G)作为评价指标
图3表明,在基于介数值的蓄意破坏下,网络的安全性能下降比随机破坏更为迅速。在蓄意破坏作用下,节点删除比例为0.682时,网络的安全值下降为0,表明网络被彻底破坏;而在随机破坏作用下,节点删除比例要达到0.818,网络的安全值下降为0,此时网络被彻底破坏。说明蓄意破坏比随机破坏具有更强的破坏力。此外,由于本文所选取的粮食供应链网络中节点之间的连接关系较多,因此,整体的抗毁性能表现较好(如表1和表2)。即使在蓄意破坏下,也需要68.2%的节点破坏,才能导致整个网络失效。
(二)边删除破坏模拟及网络安全性能评价
本文运用边删除的方法模拟对粮食供应链节点之间连接关系的破坏。分别运用随机删除边和基于介数值大小排序的删除方法,模拟对边的随机破坏和蓄意攻击。运用网络安全效率的参数值E(G)描述粮食供应链网络在遭受破坏时的网络安全状况,并对两种破坏方式作用下粮食供应链网络安全状况变化情况进行描述(如图4)。
图4表明,边随机攻击对网络安全的影响较为缓慢,而边蓄意破坏则导致网络安全参数值E(G)下降明显。说明蓄意攻击比随机攻击对粮食供应链网络的破坏力要强。同时也说明了加大对重要节点的保护,避免其受到攻击,有助于保障整个粮食供应链网络的安全性。

表1 随机破坏节点及网络安全效率值的变化情况

表2 蓄意破坏节点及网络安全效率值的变化情况
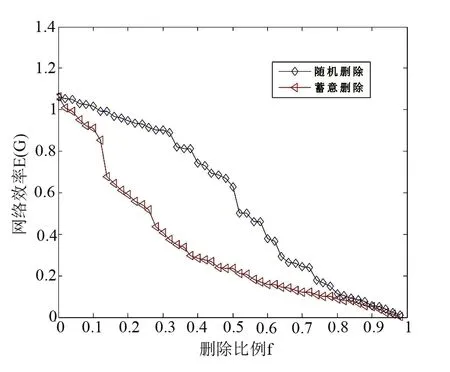
图4 随机和蓄意删除边对比分析——以网络安全效率E(G)作为评价指标
(三)随机破坏和蓄意攻击下的网络效率分析
本文运用节点删除法和边删除法模拟外部对粮食供应链网络节点的攻击。分别运用随机删除节点、边删除法和基于介数值大小排序的删除方法模拟随机破坏和蓄意攻击。运用供应链网络平均效率的参数值P(G)描述粮食供应链网络在遭受破坏时的网络安全状况,并对两种破坏方式作用下粮食供应链网络平均效率的变化情况进行描述(如图5和图6)。
图5表明,边随机攻击对网络平均效率的影响较为缓慢,而边蓄意破坏则导致网络平均效率参数值P(G)下降明显。当边的删除比例达到80%时,随机删除边和蓄意删除边对网络平均效率的影响趋于一致,表明蓄意攻击边比随机攻击边对粮食供应链网络的破坏力更强,破坏到一定程度,两者趋于一致。
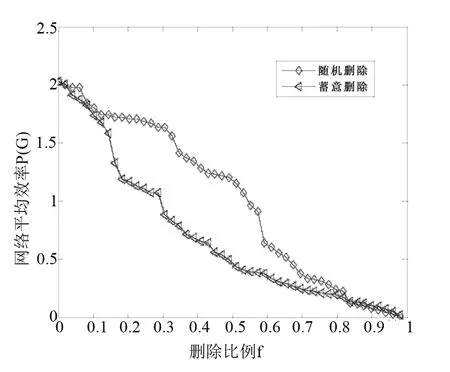
图5 随机和蓄意删除边对比分析——以网络平均效率P(G)作为评价指标

图6 随机和蓄意删除节点对比分析——以网络平均效率P(G)作为评价指标
图6表示随机攻击点导致网络平均效率呈现上下波动的趋势,最后在随机删除80%节点后,网络平均效率趋于0,而节点受到蓄意攻击后,网络的平均效率也随之下降,在60%节点遭受破坏后,网络平均效率趋于0。由此可见节点的蓄意攻击比随机攻击对网络平均效率的影响大。
六、结论
本文从粮食供应链网络的信息流、物流、商流等维度提出粮食供应链网络构建模型,并针对粮食供应链网络的特点提出两个抗毁性测度指标。该网络抗毁性测度较好地描述网络抗毁性能的变化特性。利用粮食供应链网络抗毁性仿真实验发现:(1)粮食供应链网络点随机攻击要比边随机攻击对网络安全的影响巨大。(2)粮食供应链网络的蓄意攻击表现脆弱,而对随机攻击具有鲁棒性。(3)粮食供应链网络抗毁性是由少数重要节点和边进行支撑的,因此应加强重要节点和边的保护力度,以提高网络的整体抗毁性。当然,由于粮食供应链网络的特殊性和复杂性,本文侧重从粮食供应链网络的物流环节提出网络的抗毁性分析,从信息流和商流的角度分析网络抗毁性还有待深入。
注释:
[1] 冷志杰:《大宗农产品供应链四维网络模型及应用》,《系统工程理论与实践》2005年第3期。
[2] 谭跃进、吕 欣、吴 俊等:《复杂网络抗毁性研究的主要科学问题》,中国系统工程学会第十五届年会论文集,南昌:中国系统工程学会,2008年,第108-114页。
[3]HolmeP.,KimB.J.,YoonC.N.,HanS.K., “AttackVulnerabilityofComplexnetwork”,Physical Review E,vol.65,no.5(2002),pp.1-14.
[4]AlbertR.,JeongH.,BarabasiL.,“ErrorandattacktoleranceofComplexnetworks”,Nature,vol.406,no.6794(2000),pp.378.
[5] 陈春霞:《基于复杂网络的应急物流网络抗毁性研究》,《计算机应用研究》2012年第4期。
[6] 种鹏云等:《基于复杂网络的危险品运输网络抗毁性仿真》,《复杂系统与复杂性科学》2014年第4期。
[7]NagurneyA.,DongJ.,Supernetworks:decision making for the information age.Cheltenham:EdwardElgarPublishing,2002.
[8] 张昕瑞等:《复杂供应链网络结构模型研究》,《工业技术经济》2008年第2期。
[责任编辑:黄艳林]
2016-10-08
福建省自然科学基金项目(2014J01261)
王登清, 男, 福建福州人, 福州大学经济与管理学院博士生, 福建船政交通职业学院副教授。
F307.11
A
1002-3321(2017)04-0036-06
