葡萄冷链品质的时间-温度指示器模糊推理预测

张小栓 孙格格 杨 林 郭永洪 马常阳

(1.中国农业大学工学院， 北京 100083； 2.中国农业大学食品质量与安全北京实验室， 北京 100083；3.西藏农牧学院食品科学学院， 林芝 860000； 4.中国计量大学机电工程学院， 杭州 310018；5.河南大学药学院， 开封 475004)

葡萄冷链品质的时间-温度指示器模糊推理预测

张小栓1，2孙格格1，2杨 林3郭永洪4马常阳2,5

(1.中国农业大学工学院， 北京 100083； 2.中国农业大学食品质量与安全北京实验室， 北京 100083；3.西藏农牧学院食品科学学院， 林芝 860000； 4.中国计量大学机电工程学院， 杭州 310018；5.河南大学药学院， 开封 475004)

为了验证和评价变温环境下时间-温度指示器(TTI)响应值预测农产品品质的适用性，构建了TTI模糊推理预测方法。TTI模糊推理预测是依据拟合程度高的恒温试验农产品品质实际变化经验方程，以及尽可能准确描述任意有效温度与恒温温度之间关系的隶属度函数构建预测模型，实现对任意有效温度下农产品品质预测值计算。同时设置了高低温变温试验模拟鲜食葡萄冷链物流温度特征，用上述方法对Vitsab M25-2、OnVu TTI预测玫瑰香葡萄硬度进行了参数估计与模型建立，并与TTI动力学预测值进行了对比。结果表明，面向鲜食葡萄品质感知的TTI模糊推理预测在低温下相对于TTI动力学预测有所改进，平均相对偏差分别减小了6.03个百分点和2.70个百分点；在高温下没有改进。因此在低温下可选择模糊推理预测方法。

时间-温度指示器； 预测方法； 模糊推理； 动力学

引言

时间-温度指示器(TTI)作为一种智能感知标签，能够实时感知农产品所经历的时间温度历史，反映其品质变化[1-3]，因此，常用于农产品冷链物流过程品质感知以提高冷链透明度[4-6]。感知，即根据TTI响应值预测农产品品质值。预测的前提是TTI与农产品的活化能和货架期相匹配[7]，以保证两者的有效温度Teff相等[8-11]。TTI预测的基本原理是根据TTI某时刻响应值、有效温度以及农产品的动力学参数预测农产品在该时刻的品质值。

传统的TTI预测模型是基于动力学和Arrhenius方程，预测过程为：根据动力学和Arrhenius方程推导农产品品质值-时间-温度模型、TTI响应值-时间-温度模型[12]；根据TTI在某时刻的响应值以及上述TTI响应值-时间-温度数学模型计算有效温度；根据该时刻的有效温度以及上述农产品品质值-时间-温度数学模型预测农产品在该时刻的实际品质[13-16]。

TTI动力学预测方法存在的误差一方面来源于TTI和农产品活化能差异引起的有效温度差异，另一方面来源于动力学、Arrhenius方程2次拟合引起的拟合优度降低。

本文引入模糊推理方法建立预测模型。同时，以鲜食葡萄为研究对象，以酶型TTI Vitsab M25-2、化学型TTI OnVu(激活时间为4 s)为感知工具，进行模糊推理预测值计算，并与动力学预测进行精确度对比，以期在特定情况下选择合适的预测方法提高预测准确度。

1 方法构建

TTI模糊推理预测方法的提出源于模糊推理，基于一定规则和经验关系，而不是理论数学模型[17]。它的特点是农产品品质值-时间-温度模型的获取很大程度上依据农产品的恒温试验经验方程。与基于动力学和Arrhenius方程的TTI预测方法相比较，它的区别在于农产品品质值-时间-温度模型不是恒定的，它的预测值计算依赖于有效温度的取值与恒温试验经验方程。有效温度取值是任意连续的，但是试验恒温设置是离散的、非连续的，对于联系任意变量与不连续的或非线性的变量，模糊推理提供了一种很好的解决办法。

TTI模糊推理预测方法采用Sugeno方法，主要通过插值法预测[18]。针对基于动力学和Arrhenius方程的预测方法中存在的数据回归拟合程度低的情况，Sugeno方法是最好的选择。具体地来讲，TTI模糊推理预测方法中IF-THEN规则的前提由模糊变量——温度T组成，结果是农产品品质值-时间数学方程式fT(t)。模糊规则规定了任意贮藏温度T与贮藏温度变量语言值Tn之间的关系。

IFxisAT1， THENy=fT1(t)；

IFxisAT2， THENy=fT2(t)；

IFxisAT3， THENy=fT3(t)；

⋮

IFxisATn， THENy=fTn(t)；

其中，t是贮藏时间，x是贮藏温度(即T)，AT1～ATn是温度模糊集合，fT1(t)～fTn(t)分别是对应恒温试验的品质变化经验方程，鉴于n级动力学方程拟合优度低的情况，可选取多项式拟合等方法提高拟合优度。隶属度函数可选取三角形函数、正态函数、正弦函数等，为计算方便经常选取三角形函数。如图1所示，三角形隶属度函数的中心是恒温试验所选取的各个温度，三角形的跨度是相邻温度间隔的2倍。隶属度取值范围为0～1，表示各个元素(温度)隶属于该温度模糊集合的程度。

图1 根据三角形函数定义的温度元素隶属度Fig.1 Membership degree diagram of temperature elements according to triangular function

TTI模糊推理预测方法如图2所示，步骤为：根据n级动力学方程以及Arrhenius方程推导TTI响应值-时间-温度数学模型；根据TTI响应值-时间-温度模型以及某时刻的TTI响应值计算有效温度Teff； 根据温度模糊集合与隶属度函数定义，确定有效温度Teff的隶属模糊集合AT1、AT2。根据隶属度函数以及模糊规则确定隶属度w1、w2以及对应经验方程fT1(t)、fT2(t)；根据模糊规则，该时刻TTI对农产品品质预测值为

(1)

图2 TTI模糊推理预测方法流程Fig.2 Flow chart of time temperature indicator fuzzy reasoning prediction method

2 验证试验设计

2.1 材料与处理

为了验证所提出的TTI预测方法，选择鲜食葡萄玫瑰香(产地：秦皇岛；栽培方式：温室大棚)作为监测对象。鲜食葡萄采收时选择刚成熟时期、果粒大小均匀、无机械损伤和病虫害的样品，2 h内运回实验室，预冷并装于纸箱((5±0.5) kg/箱)。硬度是鲜食葡萄玫瑰香品质和货架期评价的关键指标之一，当硬度降低到初始硬度的50%时，玫瑰香葡萄达到感官拒绝点[7，19]。

TTI选择酶型TTI Vitsab M25-2、化学型TTI OnVu(激活时间为4 s)为感知工具，响应指标分别为颜色响应函数F(X)、总色差ΔE。Vitsab M25-2 根据标签指示用手挤压即可激活，OnVu 是在(4±0.5)℃下使用紫外光激活器激活4 s完成。

根据鲜食葡萄冷链物流温度特征，设置恒温温度0、5、10、20、25、30℃，相对湿度保持85%～90%，分别计算玫瑰香葡萄和TTI的活化能和货架期，验证理论匹配度。同时，获取两者各个温度下的动力学以及Arrhenius方程，以便推导相关数学模型。

根据冷库以及冷链车环境、常温运输销售的实际温度特征，设置高低温变温历程进行模拟，用于对2种预测方法准确度进行对比验证：高温变温历程，一个温度循环周期为20℃(2 d)-30℃(1 d)-25℃(1 d)；低温变温历程，一个温度循环周期为0℃(4 d)-5℃(2 d)-10℃(2 d)-5℃(2 d)-0℃(2 d)。

2.2 测定方法

鲜食葡萄硬度测量选用CT3型质构仪。测试参数设置为：探头运行速度1 mm/s，果实变形量25%，触发力0.05 N。硬度(单位：N)为TPA(质构仪质地多面分析)双峰曲线第1个峰值[20]。

TTI颜色测量使用Minolta CR410型色差仪，采用Hunter Lab 颜色系统，测量值为L、a、b。

总色差ΔE表示2种颜色给人色彩感觉上的差别。OnVu TTI的响应指标ΔE测量以初始颜色作为基准色。ΔE随时间呈指数变化，用一级动力学方程进行拟合，公式为

ΔE=[(L-L0)2+(a-a0)2+(b-b0)2]1/2

(2)

ΔE=ΔE0exp(-kt)

(3)

式中L0、a0、b0——初始时刻的亮度、红绿色度、黄蓝色度

L、a、b——t时刻的亮度、红绿色度、黄蓝色度

ΔE0——初始时刻的总色差

k——变化速率

颜色响应函数F(X)是经过对色度C进行标准化和高斯拟合后的表达式[8-9，21]。F(X)随时间呈线性变化用零级动力学方程拟合，公式为

(4)

F(X)=kt

(5)

式中X——标准化后的色度Cmin、Cmax——TTI响应初始时刻、终点时的色度测量值

3 方法验证

首先对2种TTI与玫瑰香葡萄的活化能和货架期匹配性进行分析，然后引入动力学预测方法，对2种预测方法的过程进行逐步展开，得到预测结果，最后对预测误差进行分析。

3.1 匹配性分析

经过恒温试验获得TTI相对于鲜食葡萄的活化能之差和货架期相对误差如表1所示。活化能之差分别为5.86、5.60 kJ/mol，货架期相对误差最大分别为17.9%、15.0%，较好地符合了基于活化能和货架期的匹配原则[7]。因此，2种TTI和玫瑰香鲜食葡萄达到了初步匹配。

表1 2种TTI相对于鲜食葡萄的活化能之差和 货架期相对误差Tab.1 Activation energies differences and relative errors of shelf lives of two TTIs relative to table grape

3.2 预测参数评估与模型建立

(1)动力学预测

动力学预测过程的关键步骤为获取鲜食葡萄以及2种TTI指标的n级动力学方程、Arrhenius方程以及品质值-时间-温度数学模型，结果如表2所示，表中量符号的下角标0、t分别表示初始时刻、t时刻，R表示Arrhenius方程常数。将某时刻的TTI响应值代入TTI响应值-时间-温度数学模型得到该时刻的有效温度，随后将有效温度代入玫瑰香品质值-时间-温度数学模型即可得该时刻的动力学预测值。

(2)模糊推理预测

根据本文所构建的TTI模糊推理预测方法，以及鲜食葡萄恒温试验温度0、5、10、20、25、30℃，可以得出以下模糊规则

IFxisA0℃， THENy=f0℃(t)；

IFxisA5℃， THENy=f5℃(t)；

IFxisA10℃， THENy=f10℃(t)；

IFxisA20℃， THENy=f20℃(t)；

IFxisA25℃， THENy=f25℃(t)；

IFxisA30℃， THENy=f30℃(t)；

其中，x是有效温度，y是该有效温度下的输出。A0℃～A30℃是自定义的温度模糊集合。f0℃(t)～f30℃(t)分别是对应恒温温度下的鲜食葡萄硬度-时间数学方程，对于鲜食葡萄硬度动力学方程拟合程度不高或数据点不充分的情况，选择多项式拟合，如图3所示，以提高拟合度(表3)。任意温度与温度模糊集合之间的隶属度函数选择三角形函数，如图4所示，纵坐标表示隶属度，横坐标表示温度，每一个有效温度隶属于2个相邻的温度集合，有2个隶属度w1、w2，两者之和为1，如表4所示，其中，wAT为有效温度隶属于温度集合AT的隶属度；由于试验温度未设计15℃，因此将有效温度在10～20℃之间的时刻不计算隶属度，用试验温度代替。

图3 恒温试验下玫瑰香葡萄硬度的拟合曲线Fig.3 Fitted curves of firmness of Muscat Hamburg grape at constant temperatures

3.3 预测结果

绘制高低温变温条件下，玫瑰香葡萄硬度的动力学预测值、模糊推理预测值以及实际测量值的变化趋势，如图5～8所示。可见，图5、7的低温变温情况，模糊推理预测值更接近实际测量值；图6、8的高温变温情况，动力学预测值更接近实际测量值。

表3 恒温试验下玫瑰香葡萄硬度的决定系数R2Tab.3 Regression coefficients of firmness of Muscat Hamburg grapeat constant temperatures

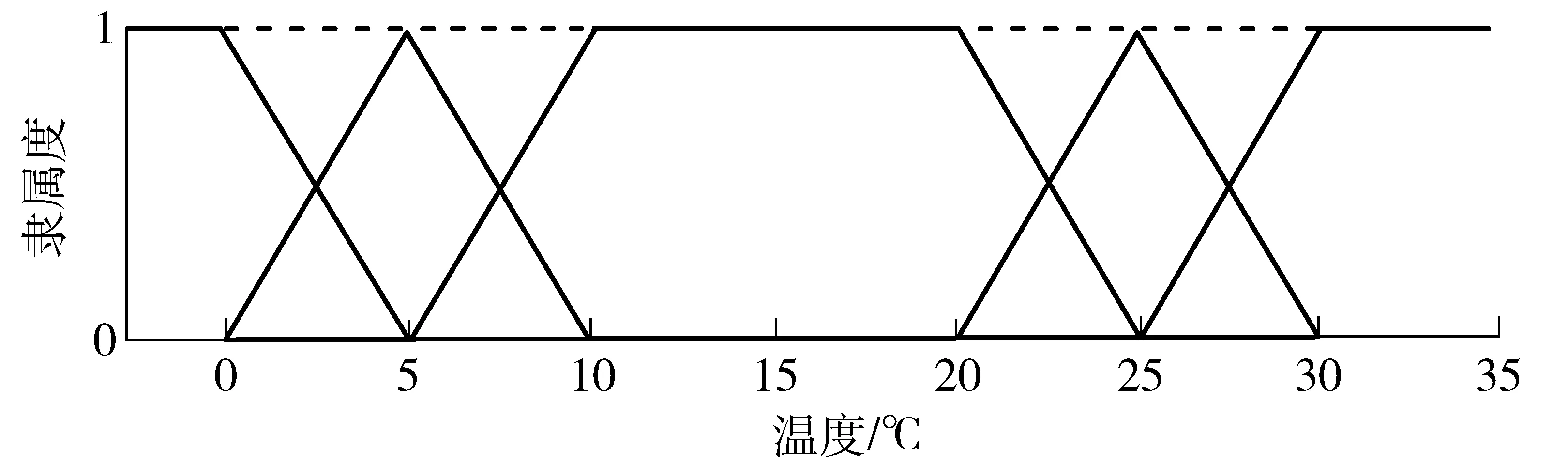
图4 根据三角形函数定义恒温温度元素的隶属度图示Fig.4 Membership degree diagram of constant temperature elements according to triangular function

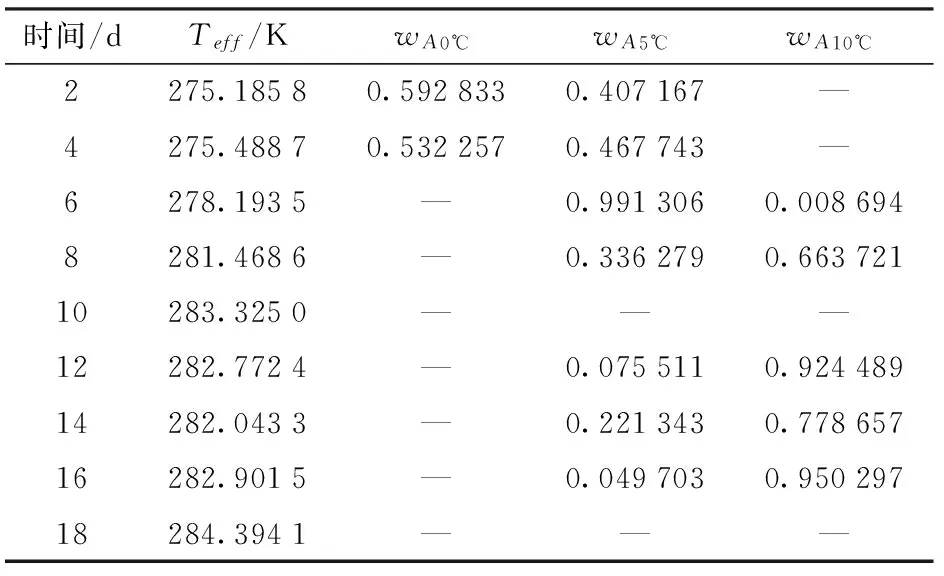
时间/dTeff/KwA0℃wA5℃wA10℃2275.18580.5928330.407167—4275.48870.5322570.467743—6278.1935—0.9913060.0086948281.4686—0.3362790.66372110283.3250———12282.7724—0.0755110.92448914282.0433—0.2213430.77865716282.9015—0.0497030.95029718284.3941———

注：“—”表示对应温度集合下的隶属度无效。

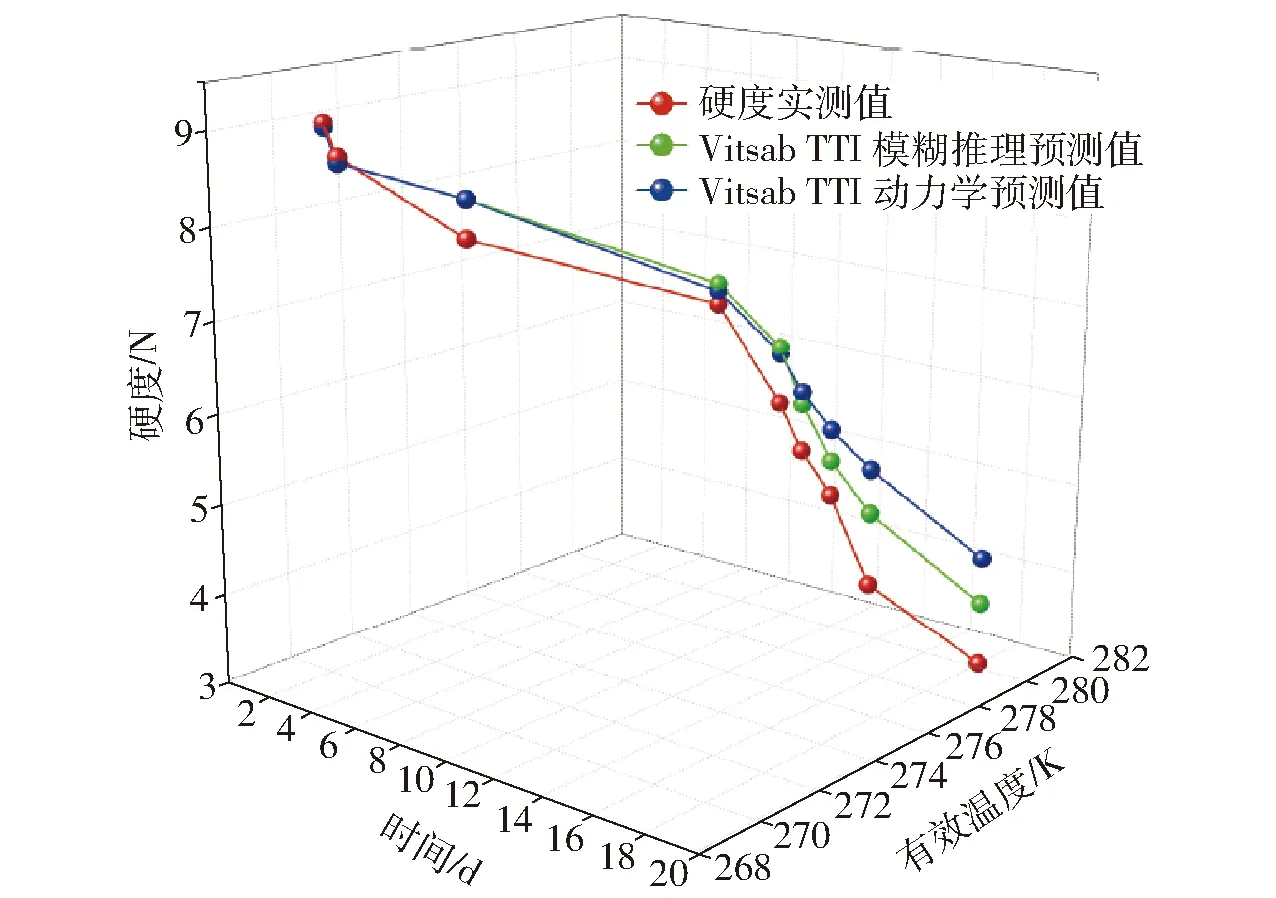
图5 低温变温试验下Vitsab M25-2 TTI预测硬度Fig.5 Predicted firmness according to Vitsab M25-2 TTI under low and variable temperature experiment

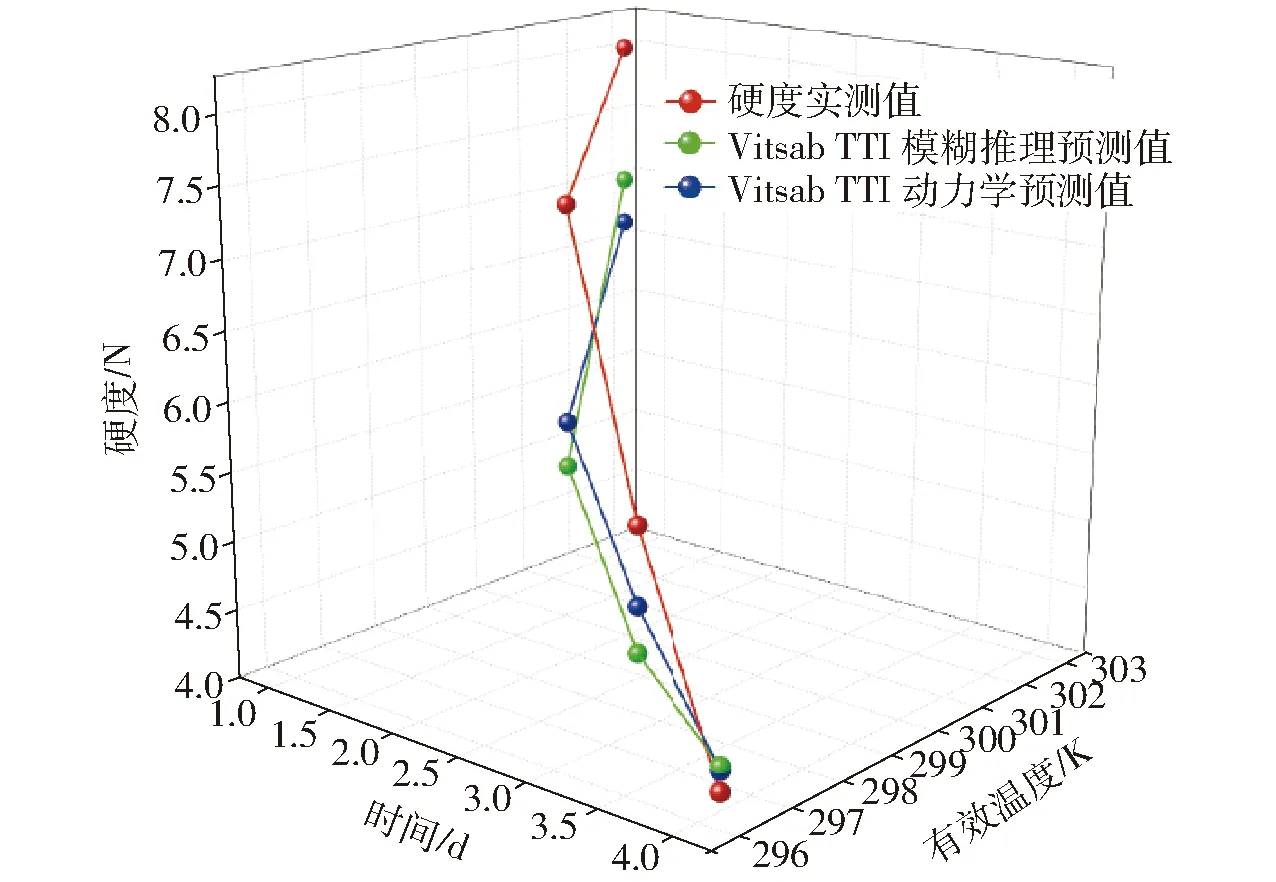
图6 高温变温试验下Vitsab M25-2 TTI预测硬度Fig.6 Predicted firmness according to Vitsab M25-2 TTI under high and variable temperature experiment

3.4 预测误差分析

为了比较2种方法预测值相对于实际试验测量值的差异程度，以试验测量值为参考，引入平均相对偏差，公式为

(6)

式中D——平均相对偏差m——TTI预测值个数fi——第i个预测值所对应时刻玫瑰香硬度的试验测量值

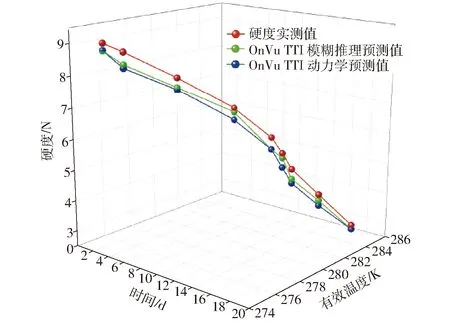
图7 低温变温试验下OnVu TTI预测硬度Fig.7 Predicted firmness according to OnVu TTI under low and variable temperature experiment

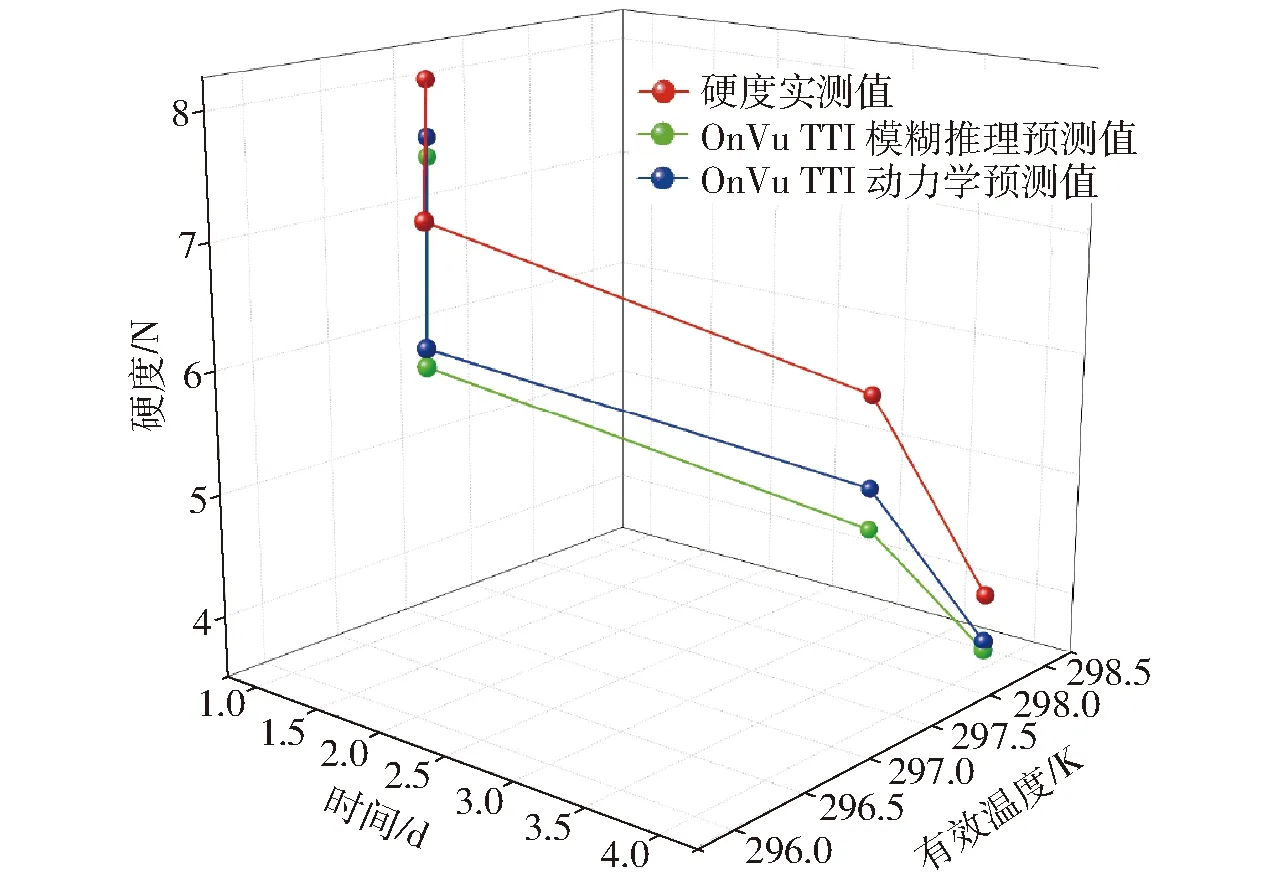
图8 高温变温试验下OnVu TTI预测硬度Fig.8 Predicted firmness according to OnVu TTI under high and variable temperature experiment

fTTIi——第i个预测值所对应时刻TTI对玫瑰香硬度的预测值

2种TTI的2种变温试验下的平均相对偏差计算结果以及模糊推理预测相对于动力学预测平均相对偏差的改进值如表5所示。其中，低温和高温试验下，Vitsab TTI的预测值个数分别为7、4，OnVu TTI的预测值个数分别为6、4。

表5 变温试验下TTI预测值的平均相对偏差Tab.5 Mean relative deviations of TTI predicted value under fluctuant temperature experiment

由图5～8以及表5可以看出，TTI模糊推理预测能够有效(D<15%)地预测玫瑰香硬度品质，TTI模糊推理预测在低温变温试验上对动力学预测做了改进，使得平均相对偏差分别减小了6.03个百分点和2.70个百分点；但是面临高温变温试验，模糊推理预测没有改进。

动力学预测准确需要保证以下2个条件：TTI与农产品的有效温度相等或相近，且准确；TTI与农产品的品质值-时间-温度数学模型关键参数准确可靠。同时，有效温度的准确依赖于关键参数的准确可靠。根据式(5)可以看出，模糊推理预测的准确度依赖于：TTI与农产品的有效温度相等或相近，且准确；有效温度的隶属度准确。可见，有效温度的误差同时存在于2种预测方法中，Teff的计算也涉及到农产品和TTI的动力学参数反应活化能Ea和方程常数k0。Teff误差之一来源于Arrhenius方程的局限性，具体表现为回归拟合计算反应速率常数k和二次线性回归计算反应活化能Ea的相关系数上。误差之二来源于TTI和农产品之间的活化能差异带来的系统误差引起的农产品品质预测值不准确。

根据上述分析，影响TTI模糊推理预测准确度的因素之一是恒温下农产品品质变化方程的确定。TTI模糊推理预测中，在描述恒温下农产品品质的变化规律时，不局限于n级动力学方程，也采用多项式、指数等任意方程，旨在提高拟合程度，最大程度上贴近实际变化情况；并且避免使用Arrhenius方程。而TTI动力学预测的误差根本上是源于n级反应动力学方程以及Arrhenius方程2次拟合导致的拟合优度降低，以及两方程本身的局限性。第2个影响TTI模糊推理预测准确度的因素是有效温度的隶属度，即隶属度函数的选定。在该研究中，模糊推理方法在低温预测时准确度更高，说明三角形函数较好地体现了玫瑰香葡萄品质低温下变化规律与各个低温恒温变化规律之间的关系；在高温下，三角形函数不能较好体现其关系。可以考虑在高温下选择其他类型的隶属度函数，或者选择在低温和高温变温试验下相对于动力学预测方法都有所改进的隶属度函数，以优化TTI模糊推理预测方法。理论上，在保证了TTI模糊推理预测的两个影响因素都准确的前提下，TTI模糊推理预测方法可以优于TTI动力学预测方法。

4 结论

(1)TTI模糊推理方法为根据TTI响应值预测农产品品质值提供了一种新的方法。该方法特征在于根据几个恒温试验农产品品质的实际变化规律建立的不定数学模型而非由Arrhenius方程推导的固定数学模型进行预测，很大程度上依据实际经验进行。关键在于选择相关系数高的拟合方程以及能够准确描述任意温度下品质变化规律与各个恒温下变化规律相关程度的隶属度函数。

(2)本研究的TTI和玫瑰香葡萄对象，模糊推理预测方法在低温下相对于动力学预测做出了改进，平均相对偏差分别减小了6.03个百分点和2.70个百分点，在高温下没有改进。实际中，采用Vitsab TTI、OnVu TTI对玫瑰香鲜食葡萄进行品质预测时，低温下可选择模糊推理预测方法，高温下选择动力学预测方法。

1 BOBELYN E, HERTOG M L, NICOLAÏ B M. Applicability of an enzymatic time temperature integrator as a quality indicator for mushrooms in the distribution chain[J]. Postharvest Biology and Technology, 2006, 42(1): 104-114.

2 PARK H R, KIM Y A, JUNG S W, et al. Response of microbial time temperature indicator to quality indices of chicken breast meat during storage[J]. Food Science and Biotechnology, 2013, 22(4): 1145-1152.

3 ZHANG X, SUN G, XIAO X, et al. Application of microbial TTIs as smart label for food quality: response mechanism, application and research trends[J]. Trends in Food Science & Technology, 2016, 51: 12-23.

4 VAIKOUSI H, BILIADERIS C G, KOUTSOUMANIS K P. Applicability of a microbial time temperature indicator (TTI) for monitoring spoilage of modified atmosphere packed minced meat[J]. International Journal of Food Microbiology, 2009, 133(3): 272-278.

5 GIANNAKOUROU M C, TAOUKIS P S. Kinetic modelling of vitamin C loss in frozen green vegetables under variable storage conditions[J]. Food Chemistry, 2003, 83(1): 33-41.

6 姚萌萌. 基于TTI的鲜食葡萄品质感知研究[D].北京：中国农业大学,2013. YAO M M. Research for quality perception of table grapes based on time temperature indicator[D].Beijing：China Agricultural University，2013.(in Chinese)

7 马常阳, 傅泽田, 姚萌萌, 等. 时间温度指示器等量线匹配适应性评估方法[J/OL]. 农业机械学报, 2014,45(7):183-188. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20140729&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2014.07.029. MA C Y, FU Z T, YAO M M, et al. Selection method of the time temperature indicator based on the contour lines[J/OL]. Transactions of the Chinese Society for Agricultural Machinery， 2014,45(7):183-188. (in Chinese)

8 TAOUKIS P S, LABUZA T P. Applicability of time-temperature indicators as shelf life monitors of food products[J]. Journal of Food Science, 1989, 54(4): 783-788.

9 TAOUKIS P S, LABUZA T P. Reliability of time-temperature indicators as food quality monitors under nonisothermal conditions[J]. Journal of Food Science, 1989, 54(4): 789-792.

10 GIANNAKOUROU M C, TAOUKIS P S. Systematic application of time temperature integrators as tools for control of frozen vegetable quality[J]. Journal of Food Science, 2002, 67(6): 2221-2228.

11 GIANNAKOUROU M C, TAOUKIS P S. Application of a TTI-based distribution management system for quality optimization of frozen vegetables at the consumer end[J]. Journal of Food Science, 2003, 68(1): 201-209.

12 陈晓宇, 朱志强, 张小栓, 等. 食品货架期预测研究进展与趋势[J/OL]. 农业机械学报, 2015, 46(8): 192-199. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150826&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2015.08.026. CHEN X Y, ZHU Z Q, ZHANG X S，et al. Research progress and trend of food shelf life prediction[J/OL]. Transactions of the Chinese Society for Agricultural Machinery，2015, 46(8): 192-199. (in Chinese)

13 ENDOZA T F M, WELT B A, OTWELL S, et al. Kinetic parameter estimation of time-temperature integrators intended for use with packaged fresh seafood[J]. Journal of Food Science, 2004, 69(3): FMS90-FMS96.

14 GIANNAKOUROU M C, KOUTSOUMANIS K, NYCHAS G J E, et al. Field evaluation of the application of time temperature integrators for monitoring fish quality in the chill chain[J]. International Journal of Food Microbiology, 2005, 102(3): 323-336.

15 HINDRA F, BAIK O D. Kinetics of quality changes during food frying[J]. Critical Reviews in Food Science and Nutrition, 2006, 46(3): 239-258.

16 SHIM S D, JUNG S W, LEE S J. Mathematical evaluation of prediction accuracy for food quality by time temperature integrator of intelligent food packaging through virtual experiments[J]. Mathematical Problems in Engineering, 2013(2013):Article ID950317.

17 李少远,王群仙,李焕芝,等. Sugeno模糊模型的辨识与控制[J]. 自动化学报,1999,25(4): 488-492. LI S Y, WANG Q X, LI H Z, et al. Identification and control based on Sugeno’s fuzzy model[J]. Acta Automatica Sinica, 1999, 25(4): 488-492.(in Chinese)

18 SUGENO M, NISHIDA M. Fuzzy control of model car[J]. Fuzzy Sets and Systems, 1985, 16(2): 103-113.

19 傅泽田, 姚萌萌, 马常阳, 等. 基于化学型时间温度指示器的鲜食葡萄品质监测[J]. 中国农业大学学报, 2013，18(6): 186-191． FU Z T，YAO M M，MA C Y，et al． Applicability of a chemical time temperature indicator as a quality indicator for table grape [J]． Journal of China Agricultural University，2013，18(6): 186-191．(in Chinese)

20 李里特 . 食品物性学[M]. 北京：中国农业出版社，2001：96-100.

21 TAOUKIS P S, KOUTSOUMANIS K, NYCHAS G J E. Use of time-temperature integrators and predictive modelling for shelf life control of chilled fish under dynamic storage conditions[J]. International Journal of Food Microbiology, 1999, 53(1): 21-31.

Time-Temperature Indicator Fuzzy Reasoning Prediction for Grape Cold Chain Quality Sensing

ZHANG Xiaoshuan1,2SUN Gege1,2YANG Lin3GUO Yonghong4MA Changyang2,5

(1.CollegeofEngineering,ChinaAgriculturalUniversity,Beijing100083,China2.BeijingLaboratoryofFoodQualityandSafety,ChinaAgriculturalUniversity,Beijing100083,China3.DepartmentofFoodScience,TibetAgricultureandAnimalHusbandryCollege，Linzhi860000,China4.CollegeofMechanicalandElectricalEngineering,ChinaJiliangUniversity,Hangzhou310018,China5.CollegeofPharmacy,HenanUniversity,Kaifeng475004,China)

With the aim to validate and accurately evaluate the applicability of time-temperature indicator (TTI) application at variable temperatures, a prediction method based on the fuzzy reasoning was built. The method was on the basis of quality experience equation of the monitored products at constant temperature experiment, which could be chosen from polynomial equation, then-th reaction kinetic equations or other equations according to the fitting coefficients. The key of this method was to build exact membership functions between arbitrate effective temperature and the constant temperature in order to obtain the predicted value at arbitrate effective temperature. The method was analyzed about Muscat Hamburg grape, Vitsab M25-2 and OnVu TTI through two fluctuant temperature experiments simulating temperature characteristics of table grape cold chain logistics. Triangle membership function was chosen in the prediction based on the fuzzy reasoning. The table grape quality predicted values based on the fuzzy reasoning and the kinetics model were compared with the actual measured values. Results showed that the TTI prediction method based on fuzzy reasoning at low fluctuant temperature made improvements (6.03 percentage points and 2.70 percentage points)vsTTI prediction method based on the reaction kinetics equations, whereas made no improvements at high fluctuant temperature. Therefore, TTI prediction method based on fuzzy reasoning could be chosen at low temperature based on the principle of merit.

time-temperature indicator; prediction method; fuzzy reasoning; kinetics

10.6041/j.issn.1000-1298.2017.08.037

2016-12-05

2017-01-12

国家自然科学基金项目(31371538)和杭州科技发展计划项目(20140432B30)

张小栓(1978—)，男，教授，博士生导师，主要从事农(渔)业系统工程与信息化技术研究，E-mail: zhxshuan@cau.edu.cn

马常阳(1988—)，男，副教授，主要从事食品物流信息技术与追溯系统研究，E-mail: macaya1024@sina.com

TS201.1

A

1000-1298(2017)08-0315-07