高寒草甸生态系统表层土壤水分时间稳定性研究

朱绪超 邵明安,2 朱军涛 张扬建

(1.中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室， 北京 100101；2.中国科学院大学资源与环境学院， 北京 100190)

高寒草甸生态系统表层土壤水分时间稳定性研究

朱绪超1邵明安1,2朱军涛1张扬建1

(1.中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室， 北京 100101；2.中国科学院大学资源与环境学院， 北京 100190)

选取西藏高原北部那曲地区一处典型的高寒草甸生态系统为研究对象，用TDR 300测量样地中2个样带共82个测点表层0～7.5 cm的土壤含水率，在2015年生长季中共测量14次。基于所测数据分析了土壤含水率的时空变异性和时间稳定性。结果表明，2015年生长季2个样带表层平均土壤含水率为26.0%，在空间上表现为弱变异性，在时间上表现为中等变异性，土壤含水率较高时，土壤水分的变异性也较高；82个测点土壤含水率的空间模式在7月份—8月初相似性较弱，在8月中旬—9月初相似性较强；土壤含水率的相对差分平均值在-11.5%～8.5%之间，相对差分标准差的平均值为8.6%，二者表现为开口向上的二次曲线关系，说明土壤含水率接近样地平均值的测点具有较高的时间稳定性，而在较干和较湿的测点，土壤含水率的时间稳定性相对较弱；时间稳定性指数、平均绝对偏差、均方根误差和最小相对差分标准差平衡法4种方法均能准确地判定土壤含水率时间稳定性最佳代表测点，利用最佳代表测点估算样带平均土壤含水率均具有较高的精度，相比较而言，最小相对差分标准差平衡法精度更高。

土壤含水率； 时空变异； 时间稳定性； 代表测点； 高寒草甸

引言

表层土壤水分作为一个重要的变量，控制着地表径流、雨水入渗、土壤蒸发、植被蒸腾等一系列生态和水文过程[1-2]。土壤水分作为高寒区植被生长重要的限制因子，其时间变化和空间分布控制着植被的格局、多样性和演替特征，对高寒草甸生态系统的功能和结构具有重要的影响。

时间稳定性是土壤含水率一个重要的特征，被定义为土壤含水率的空间模式在时间上的持续性。时间稳定性强，说明土壤含水率的空间分布模式在时间上的相似性越大。利用时间稳定性概念，可以估算样地平均土壤含水率，校正遥感反演的土壤含水率，对土壤含水率升、降尺度，插补土壤水分缺失的数据等[3-4]。土壤含水率的时间稳定性在不同的生态系统、不同的研究尺度、不同的土壤深度均获得了广泛的研究和成功的应用[5-8]。尽管有关土壤含水率时间稳定性的研究已经非常充分，然而在青藏高原地区，尤其在藏北典型的高寒草甸生态系统中，土壤含水率的时间稳定性研究尚为缺乏。

为研究高寒草甸表层土壤水分的时空变异性和时间稳定性，本文在420 m和620 m的2个交叉样带，对一典型高寒草甸82个测点表层0～7.5 cm的土壤含水率在2015年生长季共进行14次观测。分析2个样带表层土壤含水率的空间变异性和时间稳定性，评估利用不同方法判定时间稳定性代表测点的准确性，并评价最佳代表测点估算样带平均土壤含水率的精度。

1 材料与方法

1.1 研究区概况

实验在中国科学院地理科学与资源研究所藏北高原草地生态系统研究站(那曲站)(31.64°N、92.01°E，海拔高度4 600 m)进行，实验站位于中国西藏自治区那曲县正北方向19 km，地理位置处于西藏高原北部，羌塘高原的核心地带。研究区属于亚寒带半湿润季风气候，冬季漫长寒冷，仅6—8月份为生长季。1981—2014年平均气温为-0.5℃，1月份最冷，月平均气温为-11.6℃，7月份最热，月平均气温为9.6℃。研究区年均降水量455.8 mm，7月份降水最多，平均降水量为109.0 mm，6—8月降水量占全年降水量的63.7%。受厄尔尼诺的影响，研究区2015年7月经历了异常干旱，7月降水总量仅为44.2 mm，7月下旬无降水发生，生长季降水量也仅为203.5 mm。相比于降水量，研究区生长季平均气温波动较小，维持在9.6℃附近。研究区植被以高山嵩草(Kobresiapygmaea)为优势种，二裂萎陵菜(Potentillabifurca)、钉柱萎陵菜(Potentillasaundersiana)、火绒草(Leontopodiumpusillum)、苔草(Carexmoorcroftii)等丛生的植物群落生长其中。

1.2 实验和数据获取

为防止牛羊啃食，于2011年架设不规则多边形围栏对草地进行封育观测。围栏西南—东北宽约480 m，西北—东南长约700 m，总面积约33.5 hm2。在围栏中间，西南—东北方向，间距25 m布设7个测点(图1，L1～L7)，之后间距10 m布设30个测点(L8～L37)，共布设37个测点。在西北—东南方向，间距30 m布设7个测点(L38～L44)，之后间距10 m布设18个测点(L45～L62)，之后间距12 m布设20个测点(L63～L82)，2个样带共布设82个测点。用手持GPS记录各样点的经、纬度数据。用TDR 300 (Spectrum Technologies, Inc.,美国)测量表层0～7.5 cm的土壤含水率，2015年生长季共测量14次。测量时间分别为7月7日、11日、14日、18日、26日、30日，8月6日、10日、15日、19日、22日、26日、29日和9月1日。在点L1、L3、L5、L7、L12、L17、L22、L27、L32、L37(相距50 m)和点L38、L40、L42、L44、L50、L56、L62、L67、L72、L77、L82(相距60 m)处表层分别用100 cm3环刀取原状土样，用烘干法校正TDR 300，校正方程为

y=0.871 8x+5.419

(R2=0.763,p<0.001,RMSE为2.3%)

(1)

式中x——仪器实测土壤体积含水率，%y——校正后土壤体积含水率，%

实测值和校正值在p<0.001的水平上具有显著的相关性，且均方根误差(RMSE)较低，因此可认为此方程能够满足校正的精度要求。

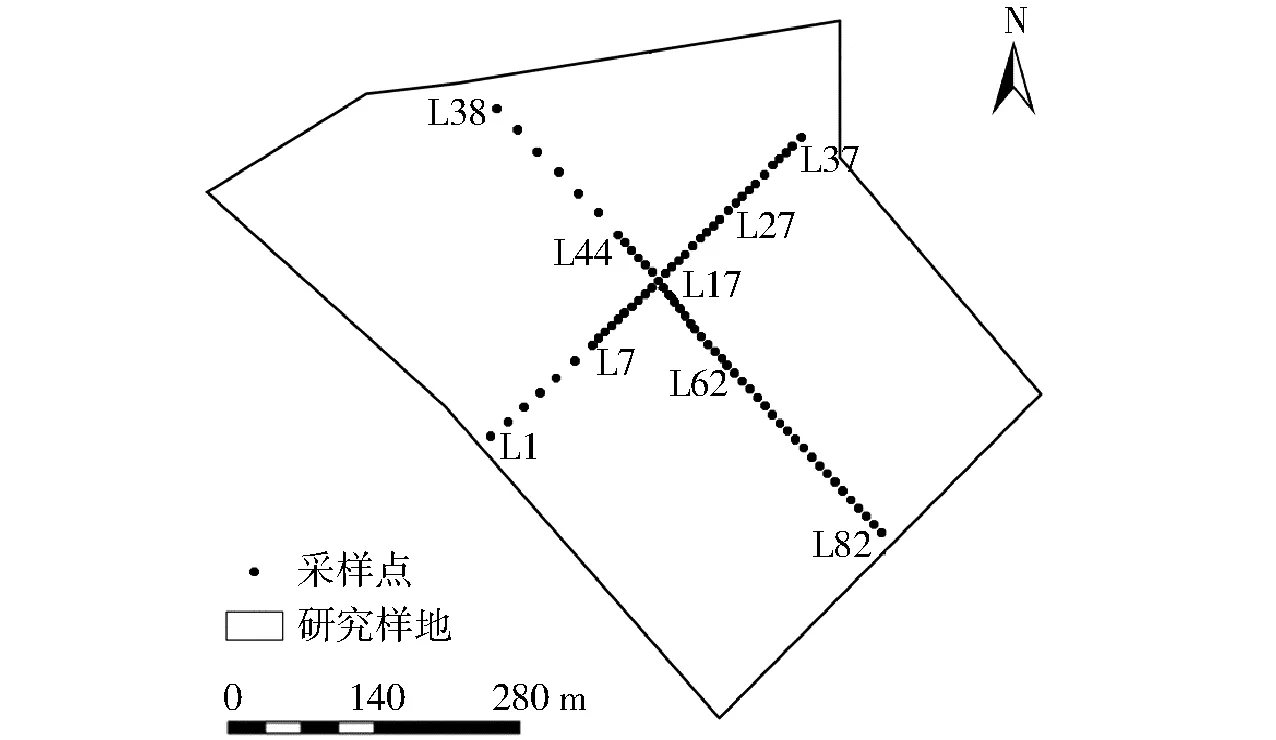
图1 样地布点位置图Fig.1 Locations of sampling points in study plot

1.3 分析方法

1.3.1 经典统计方法

利用经典统计分析方法，通过计算82个点14次测量土壤含水率的最大值、最小值、平均值、标准差和变异系数，来描述土壤含水率数据的分布情况和在时间、空间上的变异性。变异系数是标准差和平均值的比值，根据NIELSEN等[9]的划分标准，变异系数小于等于10%时为弱变异，在10%～100%之间为中等程度变异，大于等于100%时为强变异。

1.3.2 时间稳定性

采用2种方法研究土壤水分的时间稳定性，即Spearman秩相关系数法和相对差分法。Spearman秩相关系数法反映了不同观测时间下观测样点在空间模式上的相似性[10]，秩相关系数rs计算公式为

(2)

式中Rij——观测点i在时间j下土壤含水率观测值的秩

Rij′——观测点i在时间j′下土壤含水率观测值的秩

N——土壤含水率观测样点的个数，取82

rs值越接近1，表示土壤水分空间分布格局在时间上越相似，即土壤水分的时间稳定性越强。

相对差分法是根据相对差分理论建立的。根据文献[10]的研究，观测点i在观测时间j的土壤含水率相对差分值δij计算公式为

(3)

其中

(4)

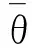
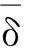
(5)

(6)

式中M——观测次数，取14

相对差分平均值一般用来判定测点土壤含水率与样地平均土壤含水率的接近程度，测点相对差分值越接近于0，其土壤含水率越能代表样地平均土壤含水率，相对差分大于和小于0，分别表示高估和低估了样地平均土壤含水率。相对差分标准差被广泛地用来判定研究区内土壤含水率的时间稳定性，其值越小，表示测点土壤含水率时间稳定性越强。当空间存在某点，其相对差分平均值接近于0，相对差分标准差又很小，则该点可在不同的含水率条件下代表研究区土壤含水率的平均值。

1.3.3 时间稳定性最佳代表测点判定方法

JACBOS等[11]和ZHAO等[12]通过将相对差分平均值和相对差分标准差合成一个指标——时间稳定性指数(ITS)，来判定时间稳定性测点，其公式为

(7)

时间稳定性指数越小的点，时间稳定性越强，其土壤含水率越能代表研究区土壤含水率的平均水平。一般认为，时间稳定性指数小于10%的点可作为时间稳定性代表性测点，值最小的点即为时间稳定性最佳代表测点。

最小相对差分标准差平衡法认为相对差分标准差最小的点为时间稳定性最佳代表测点，之后利用公式来校正测点的实测土壤含水率[1,13]，即

(8)

式中θoij——最佳代表测点i在时间j下的实测土壤含水率

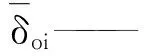
HU等[14]和GAO等[15]分别提出了利用平均绝对偏差(MABE)和均方根误差(RMSE)来判定代表性测点，计算每个测点的平均绝对偏差和均方根误差，认为数值最小的点为时间稳定性最佳代表测点。二者的计算公式分别为

(9)

(10)

二者的值越小表示土壤含水率的时间稳定性越强，最小值对应的点可认为是时间稳定性最佳代表测点。

2 结果与分析

2.1 土壤含水率的时空动态

图2为土壤含水率及其对应的标准差和变异系数以及降水量在观测期间的时间变化。由图2可直观地看出，土壤含水率具有较大的变幅，而标准差和变异系数保持相对稳定。土壤含水率的平均值为26.0%，变化范围为8.8%～37.3%。标准差均在5%以下，说明在不同的测量时间，土壤含水率的空间变化量均较小。变异系数的平均值为9.7%，说明在不同测量时间下，土壤含水率具有较弱的空间变异性。对比降水量可知，表层土壤含水率与降水量具有较好的同步性，7月份发生干旱，表层土壤含水率持续下降，8月初降水量回升，含水率稳步上升，直到8月底9月初达到相对稳定状态。

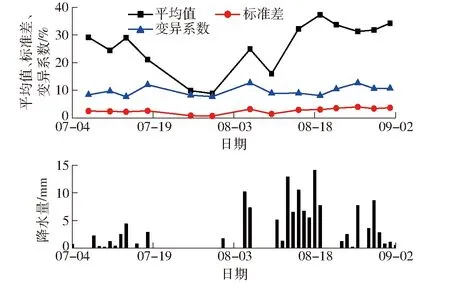
图2 空间平均土壤含水率的平均值、标准差和变异系数及对应日期的降水量Fig.2 Time series of spatial averaged soil water content and its associated standard deviation and variation coefficient along with precipitation in growing season of 2015

表1为土壤含水率在14个测次上平均值、标准差和变异系数的空间统计特征。时间平均土壤含水率在空间82个测点的平均值为26.0%，分布范围在21.7%～28.4%之间。时间上土壤含水率的标准差和变异系数在82个测点的平均值分别为9.3%和35.8%，分布范围分别为6.0%～11.3%和27.6%～40.8%。虽然土壤含水率标准差不高，但变异系数均大于10%，说明研究样地两样地表层土壤含水率在时间上表现为中等程度变异性。另外，由时间上土壤含水率的标准差和变异系数在空间上的标准差(0.9%和2.4%)和变异系数(9.98%和6.60%)可知，土壤含水率在时间上的变异性在空间82个点上没有显著的变化。

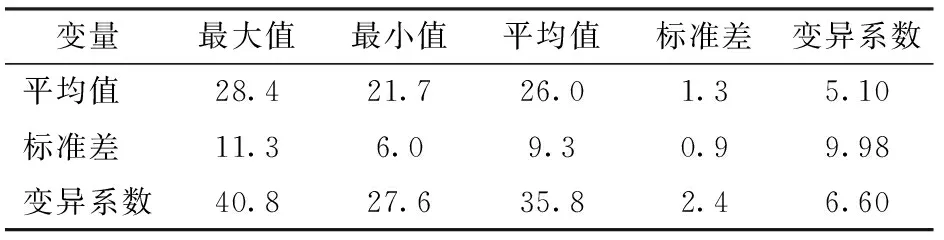
表1 土壤含水率时间上平均值、标准差和变异系数 的空间统计特征Tab.1 Statistics of spatialand temporal averaged soil water content and its associated standard deviation and variation coefficient %

ZHANG等[1]分析了中国西北荒漠地区表层土壤含水率的时空动态，数据显示在不同的观测时间下，土壤含水率在空间上具有中等程度变异性，与本研究得出的弱的空间变异性不同，这主要是研究范围、土壤性质和植被差异引起。较大的研究范围意味着土壤、地形等因素具有较大差异，土壤含水率更易发生变化。另外，其研究在荒漠地区，土壤为砂土，土壤有机质含量少，土壤具有较大的导水性能，而在高寒草甸生态系统，表层为毛毡层，土壤中多年累积的植被根系与土壤紧实地板结在一起，具有重要的保水性。此外，嵩草的枯落物累积在土壤表面，对降水和土壤的蒸发具有一定的缓冲作用，这在一定程度上减弱了土壤含水率在空间上的变化。

土壤含水率平均值与标准差的相关性(图3)表明，土壤含水率平均值与标准差在p<0.001的显著水平上具有较强的相关关系，说明在研究区土壤含水率较高时，土壤含水率的变异性也较高。这与ZHANG等[1]的研究结果相同，与BROCCA等[16]的研究结果相反。这种土壤含水率平均值与其变异性之间关系的差异，主要由于研究区的土壤属性、气候状况、植被等因素造成，同时还与土壤水分状态、研究尺度和采样策略有关[1,16]。

图3 土壤含水率平均值和标准差的关系Fig.3 Relationship between mean soil water content and associated standard deviation

2.2 土壤水分空间模式的时间变化

用Spearman秩相关系数法分析土壤含水率的空间模式[10]，土壤含水率Spearman秩相关系数见表2。由表2可以看出，前8次观测间土壤含水率的相关系数均较低，绝大多数日期对间不具有显著性，说明土壤含水率的空间模式在前8次观测时间上的相似性较弱。在后6次观测期间相关系数较高，基本在p<0.01的水平上显著，说明后6次观测的土壤含水率的空间模式具有较强的相似性。这与多数学者[1,17-19]的研究结果均不相同。本研究的前8次测量在7月和8月初，正处于异常的干旱期，土壤含水率较小，可能是导致土壤含水率时间稳定性较弱的主要原因。

2015年7月研究区共降水44.2 mm，远低于多年(1981—2014年)7月份平均降水量109.0 mm。8月开始降水恢复，整个8月共降水116.9 mm，稍高于多年8月平均降水量97.6 mm，达到正常的降水水平。研究区土壤含水率的空间模式在极端干旱的条件下(7月)相似性较弱，但在正常的降水水平下(8月)相似性较强。因此可认为，在正常的降水年份研究区表层土壤含水率具有时间稳定性。

表2 表层0～7.5 cm不同观测日期土壤含水率Spearman秩相关系数Tab.2 Spearman’s rank correlation coefficients corresponding to surface (0～7.5 cm) soil water content data measured on different dates

注：*表示相关系数在p<0.05的水平上显著，** 表示相关系数在p<0.01的水平上显著。

2.3 土壤含水率的相对差分分析

图4 相对差分平均值及其对应的标准差和时间稳定性指数排序图(灰色点表示时间稳定性指数小于5%)Fig.4 Ranked mean relative difference and its associated standard deviation along with index of temporal stability (gray points referred to locations with ITS less than 5%)

利用相对差分方法分析各测点土壤含水率的时间稳定性特征。图4为土壤含水率相对差分平均值从小到大的排列情况，及对应的相对差分标准差和时间稳定性指数曲线。平均相对差分在-11.5%～8.5%之间，极差为19.9%(表3)，比ZHANG等[1]、JIA等[17]和LI等[18]的研究均较小。这主要与研究尺度、试验布设、采样方式等有关。较大的研究尺度中，土壤、植被、地形、气象等因素具有较大的空间变异。相对差分标准差的平均值为8.6%，标准差仅为3.3%(表3)，可知各测点相对差分标准差较小且变化不大，说明土壤含水率具有较强的时间稳定性。时间稳定性指数的平均值为9.5%，标准差仅为3.6%(表3)，说明各测点具有较小且较稳定的时间稳定性指数。

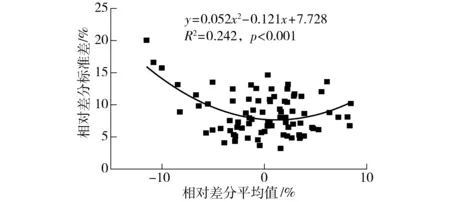
图5 土壤含水率相对差分平均值和对应标准差之间的关系Fig.5 Relationship between mean relative difference of soil moisture and its associated standard deviation

研究区7月份经历了严重的干旱，8月份又经历了丰沛的降水，因此有必要对不同土壤湿度条件下的时间稳定性进行分析。图5为土壤水分相对差分平均值与相对差分标准差间的拟合关系。可知相对差分平均值与相对差分标准差在p<0.001的水平上呈凹形二次曲线关系，相对差分平均值接近0时相对差分标准差较小，相对差分平均值绝对值越大，相对差分标准差越大。说明研究区土壤含水率接近样地平均值的测点具有较高的时间稳定性，而在较干和较湿的测点，土壤含水率的时间稳定性相对较弱。ZHANG等[1]的研究也表明土壤含水率的相对差分平均值与相对差分标准差具有显著的相关性，但相关曲线为直线，说明其研究区土壤含水率在较干测点时间稳定性较强，在较湿测点时间稳定性较弱，这可能与2个研究区不同的土壤、植被等属性有关。

2.4 土壤含水率时间稳定性代表测点

土壤水分时间稳定性最重要的应用之一就是利用代表性测点估算样地平均土壤含水率。本研究利用时间稳定性指数、平均绝对偏差、均方根误差和最小相对差分标准差平衡法4种方法来判定时间稳定性测点。时间稳定性指数是相对差分平均值和相对差分标准差合成的指标，其值越小说明土壤含水率的时间稳定性越强。本研究中时间稳定性指数最小的点为L5，值为3.6%，时间稳定性指数小于5%的测点有3个(图4中灰点)，小于10%的点共48个，占总测点数的1/2以上。图6为各测点平均绝对偏差从小到大的排序，最小值点为L5，值为2.5%，数值小于5%的点有24个，小于10%的点有72个。图7为各测点均方根误差从小到大的排序，最小值点为L5，对应的均方根误差为0.9%，小于1%的点有3个，小于2%的点有42个，占总测点数的1/2以上。最小相对差分标准差平衡法得到的具有最小相对差分标准差的测点为L5，对应的相对差分标准差为3.2%。

表4为4种时间稳定性最佳代表测点判定方法得出的代表测点估算样地平均土壤含水率的精度参数。4种方法得到的土壤含水率时间稳定性最佳测点均为L5，说明4种方法均能够准确地判定时间稳定性最佳代表测点。同时，估算结果均具有较高的R2、Nash-Sutcliffe效率系数(NSE)[20]和较小的均方根误差(表4)，说明4种方法判定的代表测点能够较准确地估算样带平均土壤含水率。相比较而言，最小相对差分标准差平衡法的均方根误差更低，NSE更接近于1，说明其具有更高的估算精度。

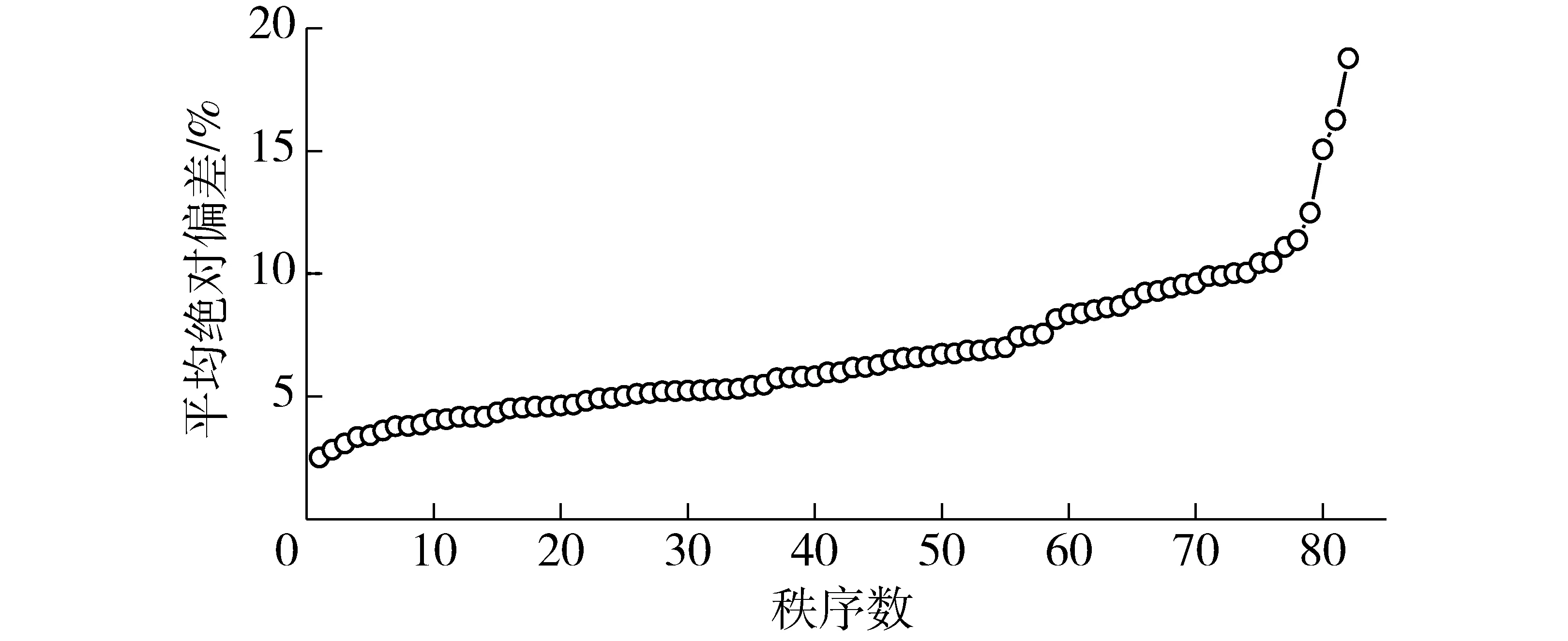
图6 土壤含水率平均绝对偏差由低到高排序图Fig.6 Ranked mean absolute bias error of soil water content

图7 土壤含水率均方根误差从低到高排序图Fig.7 Ranked root mean square error of soil water content

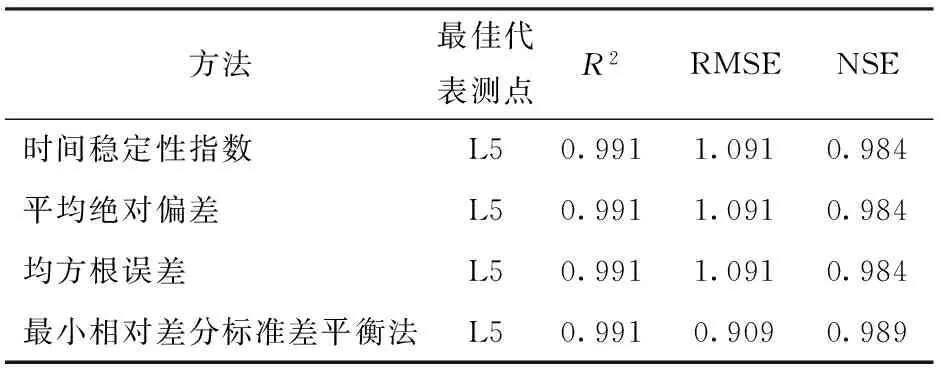
表4 4种方法判定的最佳代表测点估算样地平均 土壤含水率精度参数Tab.4 Accuracy parameters of the best representative locations identified by four methods in estimating field mean soil water content

3 结论

(1)2015年生长季，研究样地表层平均土壤含水率为26.0%，在空间上呈现出较弱的变异性，受到极端干旱和降水的影响，土壤含水率在时间上具有中等程度变异性。

(2)Spearman秩相关系数分析表明，在干旱条件下土壤含水率的空间模式具有较弱的相似性，而在降水恢复后，其空间模式的相似性显著增强。

(3)土壤含水率相对差分平均值的极差为19.9%，相对差分标准差的平均值为8.6%，二者的标准差均小于5%。相对差分平均值与相对差分标准差呈开口向上的二次曲线关系，说明研究区土壤含水率接近样地平均值的测点具有较高的时间稳定性，而在较干和较湿的测点，土壤含水率的时间稳定性相对较弱。

(4)时间稳定性指数、平均绝对偏差、均方根误差和最小相对差分标准差平衡法4种方法均能够较好地判定时间稳定性代表测点，利用判断出的最佳代表测点估算样地平均土壤含水率均具有较高的精度，其中最小相对差分标准差平衡法精度更高。

1 ZHANG P P, SHAO M A. Temporal stability of surface soil moisture in a desert area of northwestern China [J]. Journal of Hydrology, 2013, 505: 91-101.

2 VEREECKEN H, HUISMAN J A, HENDRICKS FRANSSEN H J, et al. Soil hydrology: recent methodological advances, challenges, and perspectives [J]. Water Resources Research, 2015, 51(4): 2616-2633.

3 白一茹, 邵明安. 黄土高原雨养区坡面土壤蓄水量时间稳定性 [J]. 农业工程学报, 2011, 27(7): 45-50. BAI Yiru, SHAO Ming’an. Temporal stability of soil water storage on slope in rain-fed region of Loess Plateau [J]. Transactions of the CSAE, 2011, 27(7): 45-50. (in Chinese)

4 高磊. 黄土高原小流域土壤水分时间稳定性及空间尺度性研究 [D]. 北京：中国科学院大学， 2012. GAO Lei. Temporal stability and the spatial scaling of soil moisture in a small watershed on the Loess Plateau [D]. Beijing: University of Chinese Academy of Sciences, 2012. (in Chinese)

5 王改改, 魏朝富, 吕家恪, 等. 四川盆地丘陵区土壤水分空间变异及其时间稳定性分析 [J]. 山地学报, 2009, 27(2): 211-216. WANG Gaigai, WEI Chaofu, LÜ Jiake, et al. Spatial variation and its temporal stability of soil water in hilly area of Sichuan Basin [J]. Journal of Mountain Science, 2009, 27(2): 211-216. (in Chinese)

6 VANDERLINDEN K, VEREECKEN H, HARDELAUF H, et al. Temporal stability of soil water contents: a review of data and analyses [J]. Vadose Zone Journal, 2012, 11(4)：DOI:10.2136/vzj2011.0178.

7 潘颜霞, 王新平, 苏延桂, 等. 荒漠人工固沙植被区浅层土壤水分动态的时间稳定性特征 [J]. 中国沙漠, 2009, 29(1): 81-86. PAN Yanxia, WANG Xinping, SU Yangui, et al. Temporal stability of surface soil moisture in artifically revegetated desert area [J]. Journal of Desert Research, 2009, 29(1): 81-86. (in Chinese)

8 邢旭光, 赵文刚, 马孝义, 等. 覆膜滴灌条件下棉花根层土壤盐分时间稳定性研究 [J/OL]. 农业机械学报, 2015, 46(7): 146-153. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150722&flag=1. DOI: 10.6041/j.issn.1000-1298.2015.07.022 XING Xuguang, ZHAO Wen’gang, MA Xiaoyi, et al. Temporal stability of soil salinity in root zone of cotton under drip irrigation with plastic mulch [J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 146-153. (in Chinese)

9 NIELSEN D R, BOUMA J. Soil spatial variability [M]. Wageningen: Pudoc, 1985.

10 VACHAUD G, DESILANS A P, BALABANIS P, et al. Temporal stability of spatially measured soil water probability density function [J]. Soil Science Society of America Journal, 1985, 49(4): 822-828.

11 JACBOS J M, MOHANTY B P, HSU E, et al. SMEX02: field scale variability, time stability and similarity of soil moisture [J]. Remote Sensing of Environment, 2004, 92(4): 436-446.

12 ZHAO Y, PETH S, WANG X Y, et al. Controls of surface soil moisture spatial patterns and their temporal stability in a semi-arid steppe [J]. Hydrological Processes, 2010, 24(18): 2507-2519.

13 GRAYSON R B, WESTERN A W. Towards areal estimation of soil water content from point measurements: time and space stability of mean response [J]. Journal of Hydrology, 1998, 207(1-2): 68-82.

14 HU W, SHAO M A, REICHARDT K. Using a new criterion to identify sites for mean soil water storage evaluation [J]. Soil Science Society of America Journal, 2010, 74(3): 762-773.

15 GAO X D, WU P, ZHAO X N, et al. Estimation of spatial soil moisture averages in a large gully of the Loess Plateau of China through statistical and modeling solutions [J]. Journal of Hydrology, 2013, 486: 466-478.

16 BROCCA L, MORBIDELLI R, MELONE F, et al. Soil moisture spatial variability in experimental areas of central Italy [J]. Journal of Hydrology, 2007, 333(2-4): 356-373.

17 JIA X X, SHAO M A, WEI X R, et al. Hillslope scale temporal stability of soil water storage in diverse soil layers [J]. Journal of Hydrology, 2013, 498: 254-264.

18 LI X Z, SHAO M A, JIA X X, et al. Landscape-scale temporal stability of soil water storage within profiles on the semiarid Loess Plateau of China [J]. Journal of Soils and Sediments, 2015, 15(4): 949-961.

19 GAO L, SHAO M A. Temporal stability of shallow soil water content for three adjacent transects on a hillslope [J]. Agricultural Water Management, 2012, 110: 41-54.

20 NASH J E, SUTCLIFFE J V. River flow forecasting through conceptual models: part I—a discussion of principles [J]. Journal of Hydrology, 1970, 10: 282-290.

Temporal Stability of Surface Soil Moisture in Alpine Meadow Ecosystem on Northern Tibetan Plateau

ZHU Xuchao1SHAO Ming’an1,2ZHU Juntao1ZHANG Yangjian1

(1.KeyLaboratoryofEcosystemNetworkObservationandModeling,InstituteofGeographicSciencesandNaturalResourcesResearch,ChineseAcademyofSciences,Beijing100101,China2.CollegeofResourcesandEnvironment,UniversityofChineseAcademyofSciences,Beijing100190,China)

Surface (0～7.5 cm) soil water content (SWC) was measured at 82 locations in a typical alpine meadow ecosystem on the northern Tibetan Plateau by using time domain reflectometry for 14 times during the 2015 growing season to evaluate spatial variability and temporal stability of surface SWC. Results showed that the mean SWC of the two transects during the 2015 growing season was 26.0%. SWC had a weak variability in space and a moderate variability in time. The variability of SWC was increased with the increase of SWC. The spatial pattern of SWC at the 82 measuring locations had a weak similarity during July and early August and a strong similarity from middle August to early September. The mean relative difference (MRD) of SWC was from -11.5% to 8.5% and the mean standard deviation of relative difference (SDRD) was 8.6%. MRD was correlated with SDRD in a concave curve relationship. Index of temporal stability, mean absolute bias error, root mean square error and minimum-SDRD constant methods could all identify the best representative location and the accuracy of mean SWC estimation of the representative location was high. Comparatively, the minimum-SDRD constant method had a higher accuracy. This study can provide data supplement and method innovation for SWC study in alpine meadow ecosystems.

soil water content; spatio-temporal variation; temporal stability; representative measurement location; alpine meadow

10.6041/j.issn.1000-1298.2017.08.024

2016-11-22

2016-12-29

国家自然科学基金项目(41230746)

朱绪超(1988—),男,博士生,主要从事土壤物理研究,E-mail: zhuxc.14b@igsnrr.ac.cn

邵明安(1956—),男,研究员,博士生导师,主要从事土壤物理研究,E-mail: shaoma@igsnrr.ac.cn

S152.7

A

1000-1298(2017)08-0212-07