基于二维激光扫描的立木胸径计算方法性能分析

孙 浩 刘晋浩 黄青青 赵 可

(北京林业大学工学院， 北京 100083)

基于二维激光扫描的立木胸径计算方法性能分析

孙 浩 刘晋浩 黄青青 赵 可

(北京林业大学工学院， 北京 100083)

针对目前立木胸径算法性能对比中以树干作为测量目标而无法精确评估这一问题，使用激光扫描雷达，以5种管径的PVC管作为测量目标，应用目前常用的两种几何法(切线法、弧长法)与拟合法(Taubin)，结合对应的4种角度补偿算法计算目标直径，分析各种算法误差及适用范围，对各种算法性能进行评价。结果表明，Taubin算法精度最高，考虑所有样本后，平均绝对误差为4.89%，其中测量距离为3～6 m时精度最高，平均绝对误差为3.62%。管径小于200 mm，测量距离小于2 m时，所有计算方法的误差均相对较高，其中Taubin法的平均绝对误差为10.59%，优化的弧长法与切线法的平均绝对误差分别为14.03%和13.47%。当测量距离大于2 m时，算法精度大幅度提升，Taubin算法的平均绝对误差降到6%以下。实验表明，Taubin算法在所有计算方法中精度与稳定性最高，最具有工程应用价值。

立木胸径; 二维激光扫描; 几何法; 性能分析

引言

随着科学技术的发展，激光技术由于具有高精度的测距能力而在林业测量中受到广泛关注。在各项林分参数中，立木的胸径是一个重要的指标。长期以来，立木胸径测量采用胸径尺等测量工具人工获得，效率较低，而激光扫描仪可以快速高效地对林地进行扫描，如何从大量的点云中精确获取树径信息是点云数据应用中的重要研究内容。

立木胸径测量对林业相关作业有重要意义，如林区地图绘制、林木采伐、路径规划等[1-3]。目前，已有大量学者基于二维激光扫描仪对立木胸径计算方法进行研究[4-6]。采用二维激光进行测量时，树干的水平切面被看作标准圆，通过处理圆弧状的二维点数据即可计算立木胸径[7-10]。二维点云数据的标准圆信息提取算法可以分为平面几何法与圆拟合法两类，从点云数据量上来看可分为单次扫描和多次扫描两种方式。研究表明，单次扫描时，几何法的计算精度和稳定性优于圆拟合算法，二者的精度随测量距离的增加而降低，应用圆拟合算法时，树干的表面形状对算法性能有较大影响[11-13]。采用多次扫描时，圆拟合法精度优于几何法[14-17]。各种算法的计算精度取决于距离的测量精度，当扫描树干边缘时，由于只有部分光斑接触树干，距离与方位角测量误差大大增加，使整个圆弧点集质量降低，特别是距离较远时，圆弧点集数据较少，大误差数据占比提高，最终降低了圆半径的计算精度[18-19]。针对点云数据特点，通过对点云方位角修正，可以大幅度提高计算精度。RINGDAHL等[20]建立补偿角序列，对每个修正后的点集进行计算，通过与真实立木胸径进行对比，取平均误差最小值作为角度补偿法的最终计算结果，由于实际测量中，无法确定补偿角的大小，因此其实用性较弱。王亚雄等[21]建立测量距离与最优补偿角的关系模型，通过几何法对修正后的点云进行计算，此方法具有一定的实用性，当测量距离较近时，由于目标边缘距离测量较为准确，补偿后的结果精度相对较高，而目标较远时，测量精度明显降低。对目标采用多次测量求均值方法，可以有效降低随机测量误差。

目前，所有的算法都是建立在树干截面为一标准圆这一假设基础之上，而实际上，树干表面的凹凸不平、颜色差异等因素对距离测量精度有较大影响，树干截面与标准圆也有不同程度的偏离，这些原因造成了算法对比之间不能保证单一变量原则，导致难以精确体现出算法之间精度与稳定性的差异。为了避免测量目标表面因素对算法性能的影响，本文采用二维激光扫描仪对多种径级的标准圆柱物体进行测量，应用多种主流算法计算直径，分析算法间精度与稳定性差异，为立木胸径测量提供理论支撑。

1 研究方法

1.1 测量仪器

采用德国SICK公司生产的LMS511-20100 PRO型激光扫描雷达，通过TCP/IP协议进行通讯，采用24 V锂电池作为电源。该仪器扫描范围为-5°～185°，角度分辨率为0.166 7°，可发出直径为13 mm的激光，散射角度0.264°。1～10 m的统计测距误差为6 mm，20～30 m的测距误差为14 mm，由于激光发射器封装于激光雷达内部，精确位置不易获得，但通过激光雷达扫描角度范围可以推测，激光中心位置位于激光雷达中轴线位置，距离前端66 mm处。

1.2 实验设计

首先对各种算法建立角度补偿数学模型，然后对每种方案进行对比分析，共包含2组实验：为了建立测量距离和角度补偿的数学模型，将测量目标按整数测量距离放置于激光扫描雷达前方，使得训练样本在测量距离上均匀分布；为了对各种计算方案进行有效对比，采用一组随机测试集，并加大测试样本，以有效避免小数据集导致的随机误差。

本研究以5种径级的PVC管模拟立木，第1组实验中测量距离为1～10 m，增长步长为1 m，共10种测量距离，每个距离每种径级测量100次。将PVC管呈圆弧状放置于激光雷达前，如图1所示。

图1 试验现场Fig.1 Experiment scene

图中A、B、C、D、E的管径分别为110、160、200、250、310 mm，考虑激光发射器位置后，激光扫描雷达前端到PVC管边沿位置距离为L-66 mm，其中L为每组的测量距离。应用Matlab软件对每个PVC管的点云数据进行提取与处理。

第2组实验中，测试目标仍然采用以上5种管径的PVC管，将PVC管随机放置于激光扫描雷达前方1～8 m范围内，测量70组，共350个样本，每个距离每种径级测量100次，对每个1 m间隔范围内的5种管径进行误差分析。

1.3 直径计算方法

应用几何法和圆拟合法对圆直径进行计算。几何法包含切线法、弧长法和双余弦法3种。研究表明，双余弦法计算稳定性远低于其他2种方法，故排除。圆拟合算法目前有多种，例如加权平均法、最小二乘法、Hough变换法、基于共形几何代数的拟合法等。本文采用最小二乘法。对各种计算方法进行角度补偿，一种为只移动首末点，进行边缘角度补偿，适用于所有算法；另一种为移动所有点，仅适用于圆拟合法。

1.3.1 切线法

切线法假设激光点云中的首末两点与激光中心连线相切于目标圆截面[21]，计算公式为

(1)

式中 Δθ——激光簇首末数据方位角差值ρmin——激光簇距离最小值d——圆直径

角度修正式为

(2)

式中dc——直径真实值

1.3.2 弧长法

弧长法以点云首末数据的平均值为半径作弧，将弧长作为目标直径，弧长所对应的圆心角为首末数据方位的夹角[21]。计算公式为

d=(n-1)Δβ(ρ1+ρn)/2

(3)

式中 Δβ——激光雷达角度分辨率ρ1、ρn——点云簇中首、末距离n——点云簇中点个数

补偿角计算式为

(4)

1.3.3 圆拟合法及角度补偿

最小二乘法是一种数据优化技术，通过最小化误差的平方和来寻找最优化的参数匹配。常用的最小二乘法很多，不同算法间的区别为寻找全局最优采用的方法不同，本文采用Taubin算法[22]对圆进行拟合。

边缘角度补偿与全域角度补偿规则如下：当θi<θm时，θi=θi+α；当θi>θm时，θi=θi-α。其中θi为第i个点的方位角，α为补偿角，θm为点云中距离最小点的方位角。由于无法算出补偿角度，因此建立角度补偿序列(α1,α2,…,αn)，尝试每个补偿角度值，将最接近直径真实值的角度作为最优补偿角，建立角度补偿模型。

综上所述，直径计算方案共7种，包括2种几何法(弧长法VA、切线法TD)、1种拟合法(Taubin拟合法TA)及4种与其对应的角度修正方法(角度补偿弧长法VAAM、角度补偿切线法TDAM、全域角度补偿Taubin法TAAM、边缘角度补偿Taubin法TAEM)。

2 结果与分析

2.1 角度补偿模型

几何法与拟合法的各管径补偿角随距离分布如图2所示。

4种角度补偿数学模型表示为指数函数模型，各种不同管径的角度补偿值随测量距离变化表现出很强的随机性，且离散程度较高，只有弧长法与Taubin边缘点补偿法的回归模型的拟合优度相对较好。不同管径的补偿角随测量距离的分布特征与王亚雄等[21]的角度补偿模型不一致，原因可能为本研究中使用5种管径进行建模，且测量距离相对较远，数据量更大；本文应用的角度分辨率为0.166 7°，高于王亚雄等[21]研究中采用的测量分辨率0.333°。虽然回归模型的拟合优度较低，但仍然可以对几何法与拟合法进行一定程度的修正。

2.2 测量距离对算法误差的影响

由于几何法与拟合法的原理不同，测量距离对算法性能会产生不同程度的影响。直径的3种直接计算方法与其相对应的补偿算法测量误差如图3所示。

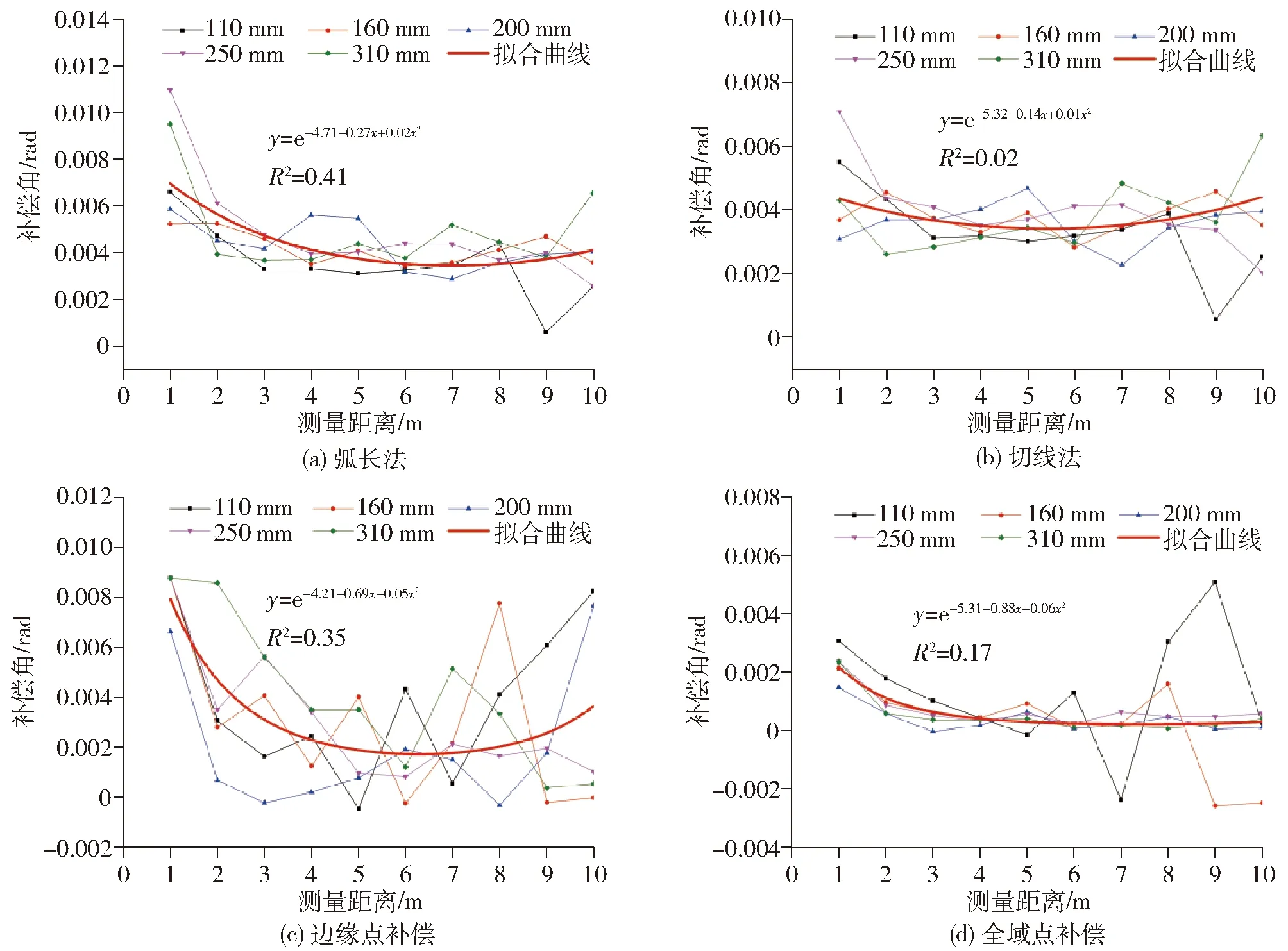
图2 不同直径的角度补偿拟合曲线Fig.2 Fitting curves of compensation angle of different diameters

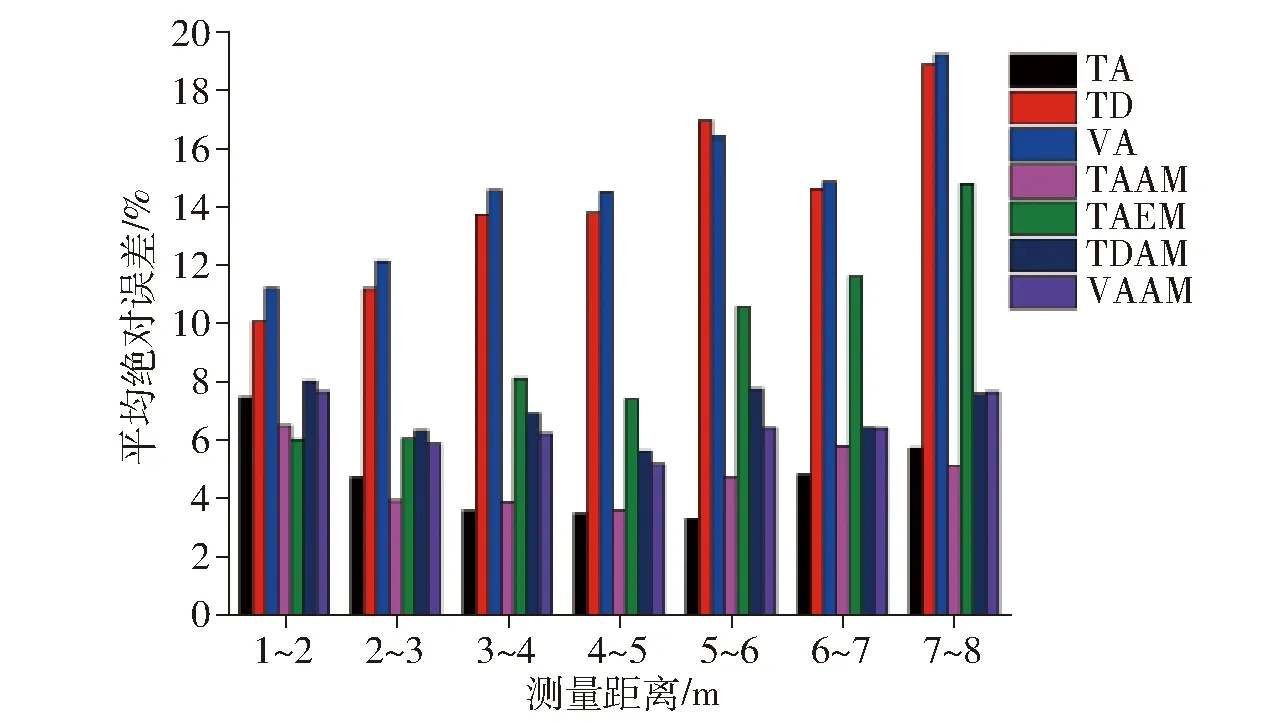
图3 平均绝对误差随测量距离的变化Fig.3 Variation of absolute error with measured distance

图3表明，两种几何法与Taubin边缘点补偿算法的误差最大，且误差随测量距离的增加而增大，优化的几何法随距离变化没有明显规律。测量距离为3～6 m时，Taubin算法精度最高。几何法的优化效果十分明显，测量距离为1～3 m时，两种几何法的平均绝对误差大于10%，而优化后算法和3种拟合法的计算误差相近，平均绝对误差在8%以下，其中拟合法的测量精度最高，TA、TAEM和TAAM法的平均绝对误差分别为6.27%、6.19%和5.38%，全域点补偿的Taubin算法精度最高。测量距离大于3 m时，边缘点补偿的Taubin算法精度逐渐减小，已不具有工程应用价值；Taubin算法与其全域点修正法的精度最高，平均绝对误差分别为4.35%和4.79%，测量误差随测量距离增加而略有增大；弧长法和切线法的优化算法测量精度次之，平均绝对误差分别为6.54%和7.00%，误差随测量距离增加没有明显变化。

2.3 被测目标直径对算法误差的影响

直径计算方法的精度与数据点云数量密切相关，点云数量会对不同的算法产生一定的影响。不考虑距离因素，5种管径的不同算法间的误差对比如图4所示。

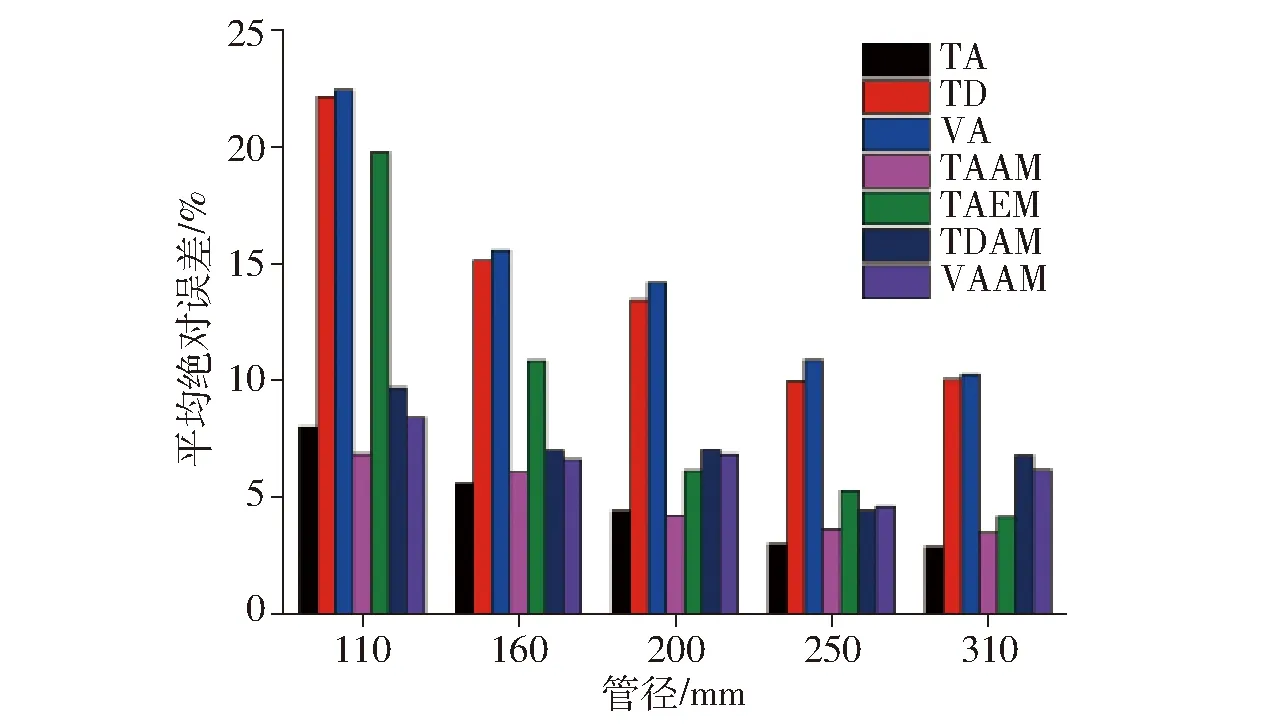
图4 平均绝对误差随管径的变化Fig.4 Variation of mean absolute error with PVC diameter

如图4所示，各种算法的误差随管径的增大而逐渐减小，被测物体截面对算法精度有较大影响。管径为110 mm时，Taubin算法的平均绝对误差为8.12%，其全域点补偿算法精度最高，平均绝对误差为6.96%，精度有一定提高。两种几何优化算法次之，平均绝对误差在8%～10%之间。管径大于等于160 mm时，Taubin算法精度最高，其中管径为250 mm和310 mm时，平均绝对误差分别为3.10%和2.99%，修正后的算法误差明显增加。各种管径下的几何法优化效果显著，管径为110 mm时，切线法测量精度由22.69%提高到9.80%，弧长法精度由22.69%提高到8.54%。可以看出，虽然几何法补偿后精度大幅度提高，但仍然小于Taubin算法精度。

2.4 算法误差综合分析

算法误差来源较多，如激光雷达固有系统误差，由于激光反射强度过低导致的测量误差等。对于圆弧形态截面的测量，测量距离误差将上升为圆弧形态误差，即测距误差与测量距离的比值、测距误差与被测物体的截面直径的比值也会成为描述圆弧形态准确程度的影响因素。5种管径随距离变化的7种算法误差对比见表1。

如表1所示，当管径小于等于200 mm，测量距离为1～2 m时，无论是Taubin算法还是几何法均具有较高的误差，其中Taubin法的平均绝对误差为10.59%，优化的弧长法与切线法的平均绝对误差分别为14.03%和13.47%；当管径大于200 mm时，Taubin算法与几何修正法的测量误差小于5%。本文使用的激光扫描雷达，1～10 m范围内时，测距误差为6 mm，当管径和测量距离较小时，测量误差占测量距离和管径的比重相对较高，降低了点云描述圆弧的精确程度。因此，对于低质量的点云数据，无论采用何种方法，测量都具有较大误差。

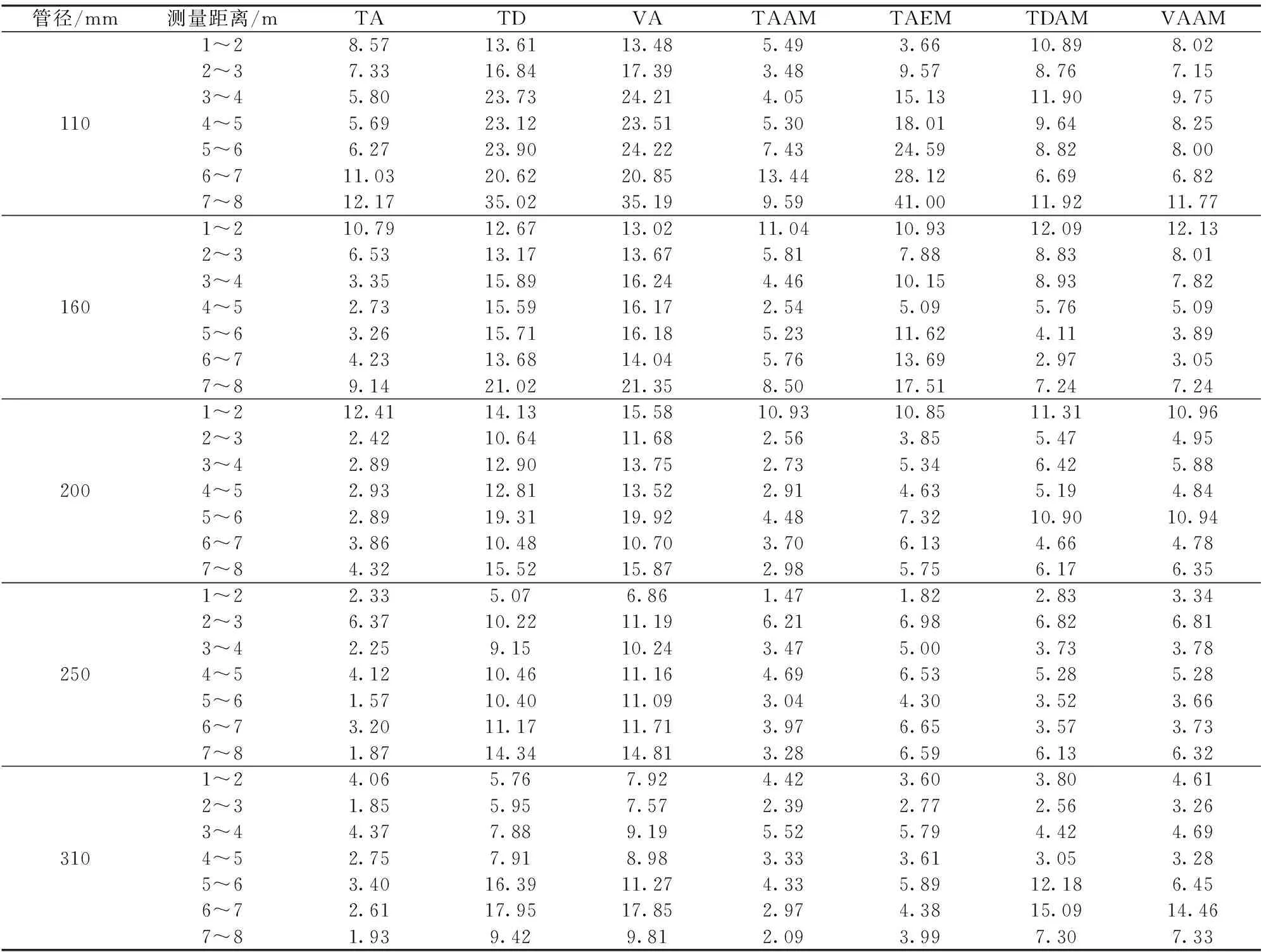
表1 不同算法误差对比Tab.1 Error comparison for different algorithms %

当测量距离大于2 m时，Taubin法的平均绝对误差降到6%以下。且测量稳定程度大大高于几何法。对于优化后的几何法，除管径为110 mm以外，其余大部分测量误差都小于8%。工程应用中，Taubin算法由于使用拟合法，考虑点云簇中的所有点，因此计算效率小于几何法。对于几何法虽然精度上略小于Taubin算法，但计算效率较高，在精度要求不高且注重测量效率时更为适用。当测量距离大于6 m时，Taubin算法的精度与稳定性略有降低，此时由于测量距离较远，测距误差增大，其占测量距离和目标直径的比重有所增加，导致算法精度降低。

综上所述，几何法由于仅使用1个或2个距离值与边缘方位角，低质量的数据所占比重相对较高，使得计算误差相对较大。Taubin算法使用目标截面上的所有点作为计算数据，由于误差较高的边缘点数量占比较低，容错能力大大增加，具有更高的计算精度与稳定性。对于Taubin法的点补偿算法，由于边缘点方位角误差具有随机性，很难建立一种合适的补偿模型，因此，Taubin算法的全域点补偿法与Taubin算法精度相近，而其边缘点补偿法的精度反而大大降低，不具有工程应用价值。

3 结束语

对比了目前3种普遍采用的立木胸径点云计算方法，和其对应的角度补偿改进算法，应用标准圆截面的PVC管作为测量目标，对各种算法的计算精度与适用范围进行分析。角度补偿后Taubin算法在7种方案中精度最高，计算精度随测量距离的变化不符合单调函数变化规律。计算精度首先随测量距离增加而逐渐增加，当超过一定测量距离后，精度逐渐降低，其中测量距离为3～6 m时精度最高，因此工程应用中，需要保持在合适的距离，以便于获得最高的测量精度。目标直径对计算精度有较高影响，几何法与拟合法的计算精度随测量目标的直径增大而逐渐提高，当管径小于200 mm时，Taubin全域点补偿算法精度最高。当管径大于等于200 mm时，Taubin法精度最高。对于所有算法，管径较小且测量距离小于2 m时，均会引起较大误差，优化的弧长法与切线法虽然精度大幅度提升，但测量误差仍然大于Taubin法。当测量距离大于2 m时，各种测量方案的精度大幅度提升，Taubin算法的平均绝对误差降到6%以下。实际工程中，建议测量小径级目标时，测量距离要适当增大。

1 HELLSTROM T, RINGDAHL O. Follow the past: a path tracking algorithm for autonomous forest vehicles[J]. International Journal of Vehicle Autonomous System, 2006, 4(2)： 216-224.

2 SPRIGGS R A, VANDERWEL M C, JONES T A, et al. A simple area-based model for predicting airborne LiDAR first returns from stem diameter distributions: an example study in an uneven-aged, mixed temperate forest[J]. Canadian Journal of Forest Research, 2015, 45(10): 1338-1350.

3 ZHENG Y L, LIU J H, ZHANG S, et al. Extraction of trees stem diameters at breast height by terrestrial laser sensor for selective cutting[J]. Sensors and Transducers Journal, 2014, 164(2): 65-70.

4 MATTI O, MIKKO M, KOSTI K, et al. Tree measurement and simultaneous localization and mapping system for forest harvesters[C]∥The 6th International Conference on Field and Service Robotics, 2008, 42: 369-378.

5 THOMAS H, PAR L, TOMAS N, et al. Autonomous forest vehicles: historic, envisioned, and state-of-the-art[J]. International Journal of Forest Engineering, 2009, 20(1): 31-38.

6 THOMAS H, OLA R. Real-time path planning using a simulator-in-the-loop[J]. International Journal of Vehicle Autonomous Systems, 2009, 7(1): 56-72.

7 HENNING J G, RADTKE P J. Detailed stem measurements of standing trees from ground-based scanning lidar[J]. Forest Science, 2006, 52(1): 67-80.

8 翟长远，赵春江，王秀，等. 树型喷洒靶标外形轮廓探测方法[J].农业工程学报，2010，26(12)：173-177. ZHAI Changyuan, ZHAO Chunjiang, WANG Xiu,et al. Probing method of tree spray target profile[J]. Transactions of the CSAE, 2010, 26(12): 173-177. (in Chinese)

9 王建利，李婷，王典，等. 基于光学三角形法与图像处理的立木胸径测量方法[J/OL].农业机械学报，2013，44(7)：241-245. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20130742&flag=1. DOI：10.6041/j.issn.1000-1298.2013.07.042. WANG Jianli, LI Ting, WANG Dian, et al. Measuring algorithm for tree’s diameterat breast heightbased on optical triangular method and image processing[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(7): 241-245. (in Chinese)

10 黄晓东，冯仲科. 基于数码相机的样木胸径获取方法[J/OL].农业机械学报，2015，46(9)：266-272. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20150939&flag=1. DOI:10.6041/j.issn.1000-1298.2015.09.039. HUANG Xiaodong, FENG Zhongke. Obtainment of sample tree’s DBH based on digital camera[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 266-272. (in Chinese)

11 JUTILA J, KANNAS K, VISALA A. Tree measurement in forest by 2D laser scanning[C]∥International Symposium on Computational Intelligence in Robotics and Automation, 2007:491-496.

12 BRUNNER A, GIZACHEW B. Rapid detection of stand density, tree positions, and tree diameter with a 2D terrestrial laser scanner[J]. European Journal of Forest Research, 2014, 133(5):819-831.

13 SIMONSE M, ASCHOFF T, SPIECKER H, et al. Automatic determination of forest inventory parameters using terrestrial laser scanning[C]∥Proceedings of the Scandlaser Scientific Workshop on Airborne Laser Scanning of Forests, 2003, 6:251-257.

14 SCHILLING A, SCHMIDT A, MAAS H G. Automatic Tree detection and diameter estimation in terrestrial laser scanner point clouds[C]∥Computer Vision Winter Workshop, 2011: 75-83.

15 ASCHOFF T, THIES M, SPIECKER H. Describing forest stands using terrestrial laser-scanning[J]. International Archives of Photogrammetry, 2004, 35(5): 237-241.

16 MASS H G, BIENERT A, SCHELLER S, et al. Automatic forest inventory parameter determination from terrestrial laser scanner data[J]. International Journal of Remote Sensing, 2008，29(5):1579-1593.

17 ANTONARAKIS A S. Evaluating forest biometrics obtained from ground lidar in complex riparian forests[J]. Remote Sensing Letters, 2011, 2(1): 61-70.

18 YAO T, YANG X, ZHAO F, et al. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar[J]. Remote Sensing of Environment, 2011, 115(11): 2965-2974.

19 JUPP D L, CULVENOR D S, LOVELL J L, et al. Estimating forest LAI profiles and structural parameters using a ground-based laser called Echidna[J]. Tree Physiology, 2009, 29(2): 171-181.

20 RINGDAHL O, HOHNLOSER P, THOMAS H, et al. Enhanced algorithms for estimating tree trunk diameter using 2D laser scanner[J]. Remote Sensing, 2013, 5(10): 4839-4856.

21 王亚雄，康峰，李文彬，等. 基于2D激光探测的立木胸径几何算法优化[J/OL]. 农业机械学报，2016，47(6): 290-296. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160638&flag=1. DOI：10.6041/j.issn.1000-1298.2016.06.038. WANG Yaxiong, KANG Feng, LI Wenbin, et al. Optimization of geometry algorithm for DBH of standing tree on 2D laser detection[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6): 290-296. (in Chinese)

22 TAUBIN G. Estimation of planar curves, surfaces, and nonplanar space curves defined by implicit equations with applications to edge and range image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(11): 1115-1138.

Performance Analysis of Calculation Method for DBH of Standing Tree Based on Two Dimensional Laser Scanning

SUN Hao LIU Jinhao HUANG Qingqing ZHAO Ke

(SchoolofTechnology,BeijingForestryUniversity,Beijing100083,China)

Study on tree DBH algorithm based on two-dimensional laser has engineering significance to forestry surveying. In order to solve the problem that the performance of algorithm can not be evaluated effectively when the trunk was taken as the measurement target. Five kinds of PVC tubes were scanned with laser scanning radar. Two kinds of geometric methods (tangent method and arc length method) and fitting method (Taubin), which are commonly used at present, corresponding four optimization algorithms were used to calculate diameter. The error and suitable range of the algorithm were analyzed and the performance of various algorithms was assessed. Results showed that Taubin algorithm had the highest precision, considering all samples the mean absolute error was 4.89%. It had the highest precision when measuring distance rang from 3 m to 6 m in which the mean absolute error was 3.62%. The errors of all calculation methods were relatively high when the pipe diameter was less than 200 mm and measuring distance was less than 2 m. The mean absolute error of Taubin method was 10.59%, the mean absolute error of optimized arc length method and tangent method were 14.03% and 13.47%, respectively. The accuracies of measured values of radius were greatly improved when measuring distance was further than 2 m. The mean absolute error of the Taubin algorithm was reduced below 6%. Experimental results showed that the Taubin algorithm had the highest accuracy and stability in all methods, which was valuable for engineering applications.

DBH of standing tree; two dimensional laser scanning; geometry algorithm; performance analysis

10.6041/j.issn.1000-1298.2017.08.021

2017-05-08

2017-06-12

林业公益性行业科研专项经费项目(201504508)和“十二五”国家科技支撑计划项目(2015BAD07B00)

孙浩(1989—)，男，博士生，主要从事森林工程装备及其自动化研究，E-mail： 251045257@qq.com

刘晋浩(1958—)，男，教授，博士生导师，主要从事林业装备自动化及智能化研究，E-mail： liujinhao@vip.163.com

S24； S758.1

A

1000-1298(2017)08-0186-06