直角坐标系下立体层析FRECHET导数求取修正问题探讨

周嘉欣,熊 凯,杨 锴

(同济大学海洋与地球科学学院,上海200092)

直角坐标系下立体层析FRECHET导数求取修正问题探讨

周嘉欣,熊 凯,杨 锴

(同济大学海洋与地球科学学院,上海200092)

直角坐标系下立体层析反演所需的FRECHET导数是地表观测到的扰动量对模型空间初始扰动量的一阶导数。当傍轴射线没有到达地表时,FRECHET导数的计算会产生误差,从而影响反演精度,必须对其进行修正。利用中心射线地表出射点坐标、傍轴射线最后一点坐标以及傍轴射线最后一点与其地表预期出射点坐标差之间存在的三角关系,换算出中心射线地表出射点与傍轴射线地表预期出射点的坐标差和初始位置扰动之间的线性关系,从而求取正确的FRECHET导数。上述换算与前人提出的多追踪一小段射线的计算公式等价,但是计算成本更低。数值算例证实了修正方法的正确性以及直角坐标系下立体层析实施这种修正的必要性。

立体层析反演;傍轴射线;FRECHET导数;直角坐标系

在工业界实施偏移速度建模的历史中,基于射线理论的层析反演扮演着非常重要的角色[1-4]。即便在全波形反演成为学术界和工业界研究热点的今天,层析反演依然不可或缺。学者们已经证明,在全波形反演的第一阶段,即反演低波数速度成分的阶段,全波形反演基本上等价于层析反演[5-6]。在诸多层析反演方法中,立体层析是一种极具特色的层析反演算法,它重新定义了数据空间和模型空间,炮检点坐标和对应的射线参数被纳入其中,实现了对速度结构、反射点位置和反射层局部形态的联合反演。目前,立体层析提供的高分辨率速度模型不仅能够满足偏移成像的需求,而且能够为全波形反演以及储层反演提供高质量的初始模型[7-13]。

传统立体层析方法是在射线中心坐标系下建立层析矩阵方程的。BILLETTE等[13]和LAMBARE[14]在射线中心坐标系下推导了二维立体层析所需的模型空间各分量扰动与数据空间各分量扰动之间的线性关系,成功实现了射线中心坐标系下的二维立体层析反演。在此基础上,CHALARD等[15]实现了射线中心坐标系下的三维立体层析,在三维射线中心坐标系下使用降阶汉密尔顿算子推导出三维立体层析所需的各个导数关系。YANG等[16]指出,三维射线扰动理论在射线中心坐标系下实现并非最佳选择,因为在射线中心坐标系下构造三维傍轴射线追踪所需的传播矩阵时,涉及到对垂直于中心射线的各个方向求关于速度二阶导数的计算,这个计算非常耗时。在三维直角坐标系下实现傍轴射线追踪则不存在上述问题。

尽管在直角坐标系下实施三维傍轴射线追踪对于降低计算成本有很大优势,但是有一个关键的环节——FRECHET导数矩阵的计算存在误差,需要对其进行修正。在直角坐标系下实施傍轴射线追踪时,除射线垂直出射地表外,一般情况下中心射线与傍轴射线不可能同时到达地表。当中心射线到达地表时,傍轴射线往往还没有到达。建立立体层析矩阵应该使用傍轴射线到达地表时其对应的传播矩阵中的各个元素,如果采用傍轴射线没有到达地表时的传播矩阵元素,那么地表接收到的数据空间的扰动量与地下模型空间的扰动量之间的线性关系将无法通过射线扰动理论正确得到。这意味着FRECHET导数矩阵的计算将产生误差,只有对这个误差实施修正才能正确实现直角坐标系下的立体层析。

NAG[17]提出多追踪一小段傍轴射线使得傍轴射线到达地表的思路,需要计算出对应于多追踪这一小段的积分步长,它涉及到地表面法向量与坐标差向量的点积以及除法运算。如果对每条射线都实施上述运算,则会增加不少计算量。通过分析我们发现,当中心射线到达地表但傍轴射线并没有到达地表时,中心射线地表出射点坐标、傍轴射线最后一点坐标以及傍轴射线最后一点与其地表预期出射点的坐标差之间存在一个近似的三角关系。利用这个三角关系,在傍轴射线没有到达地表的情况下依然可以换算出立体层析所需要的中心射线地表出射点坐标与傍轴射线地表预期出射点的坐标差和地下射线出射点初始位置之间的线性关系,从而求取正确的FRECHET导数。本文首先从理论上证明了上述三角关系换算公式与NAG[17]多追踪一小段射线的计算公式等价,然后通过数值算例证实了该换算公式的正确性。理论数据反演结果表明,该换算公式能使直角坐标系下立体层析反演的精度得到明显提高。

1 直角坐标系下立体层析线性关系

立体层析同时利用了走时信息和同相轴的局部斜率信息来估计背景速度模型,因此其数据空间和模型空间与传统走时层析方法明显不同。图1给出了二维立体层析数据空间各分量与模型空间各分量。地表能接收到的数据为d=(Sx,Rx,TSR,pSx,pRx),其中Sx,Rx为炮检点的横坐标;TSR为射线对双程旅行时;pSx,pRx为炮检点处射线参数水平分量。一个局部同相轴可以唯一地对应于一个炮点和一个接收点位置Sx和Rx,叠前道集内拾取的斜率pSx和pRx,以及双程走时TSR。“立体层析”这一提法来源于其数据空间引入的炮检点处射线参数水平分量pSx和pRx对反演产生的强约束[14]。模型空间为m=(x0,z0,θS,θR,v),其中x0,z0为地下反射点坐标;θS表示地下反射点向炮点一侧出射的射线与法线方向的夹角;θR表示地下反射点向检波点一侧出射的射线与法线方向的夹角;v表示介质速度。

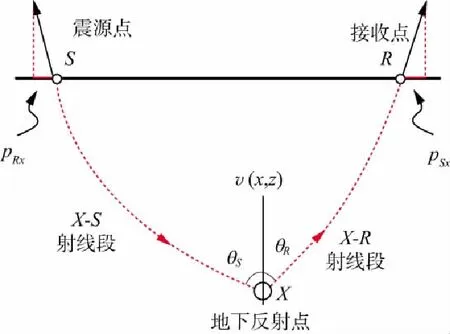
图1 二维立体层析数据空间各分量与模型空间各分量

立体层析将传统反射层析由炮点到反射点再到检波点的反射过程变为由地下反射点分别向炮点和检波点发出射线的两个透射过程。数据空间残差Δd和模型空间残差Δm之间的线性关系可以表示为:

(1)

(1)式中的系数矩阵F即为二维立体层析的FRECHET导数矩阵。其完整形式如下:

(2)

式中:σ为尺度量纲因子,用以解决数据量级差别过大的问题。注意地面炮点一侧观测到的坐标和射线参数与检波点一侧对应的地下反射点处张角和方位角无关。这一事实在检波点处同样存在,因此有

(3)

另由Fermat原理,在射线两端及背景速度固定不变时,走时不变且最小。因此模型空间地下散射角的一阶扰动对旅行时TSR不会造成影响,有

(4)

根据(3)～(4)式,可将FRECHET导数矩阵简化为:

(5)

注意(5)式中除了旅行时TSR关于模型空间的导数无需通过射线扰动理论计算外,其余各个分量关于模型空间的导数均需要通过射线扰动理论计算,具体推导过程见下文。

2 二维直角坐标系下的汉密尔顿传播算子及傍轴射线追踪系统

二维直角坐标系下汉密尔顿算子形式为:

(6)

为表达方便,我们不妨用x1表示x,x3表示z,p1表示px,p3表示pz,那么二维直角坐标系下的射线追踪方程组可表示为:

(7)

由汉密尔顿方法,可得其具体形式为:

(8a)

(8b)

方程(8)由4个一阶微分方程组成。当某条参考射线(中心射线)的初始射线场有一个微小的扰动量时,扰动的射线会在中心射线附近传播,该扰动射线称为傍轴射线。傍轴射线通过计算其相对中心射线的相空间扰动量得到。对汉密尔顿系统两端取全微分,可得到直角坐标系下的傍轴射线追踪系统:

(9)

将上述傍轴射线追踪系统写为如下矩阵形式:

(10)

其中,δη=(δx1,δx3,δp1,δp3)T,

S=

(10)式即为二维直角坐标系下的运动学傍轴射线追踪系统,表达了射线场的初始扰动[δ(x1)0,δ(x3)0,δ(p1)0,δ(p3)0]与射线轨迹上任意一点的射线场扰动(δx1,δx3,δp1,δp3)之间的线性关系。二维直角坐标系汉密尔顿形式下的速度扰动(δv)对汉密尔顿传播算子的线性影响可以表达为:

(11)

其中δH为汉密尔顿扰动算子:

(12)

(13)

对(11)式表示的汉密尔顿算子关于δζ=(δx1,δx3,δp1,δp3)T全微分,可得:

(14)

A矩阵表示背景场的傍轴系数矩阵;B矩阵表示速度扰动造成的傍轴系数矩阵,各元素可以通过对扰动的汉密尔顿传播算子关于射线参数和空间坐标参数的导数求得,具体表示为:

根据GILBERT等[18],可求得(14)式的传播矩阵形式解为:

(15)

射线传播矩阵Q-1(t1,t0)是傍轴射线追踪的一组基本解,即分别代入(1,0,0,0)、(0,1,0,0)、(0,0,1,0)、(0,0,0,1)这4组初始值计算的4组解构成的4×4矩阵:

因此(15)式可以写为如下显式形式:

(16)

其中,

用(16)式可以建立二维直角坐标系下立体层析所需数据空间分量中除旅行时TSR外所有分量对于模型分量的一阶线性扰动关系。为符合表达上的习惯,以下我们依然用x表示x1,z表示x3,px表示p1,pz表示p3,这时炮点坐标和炮点射线参数与模型空间各分量的线性关系可以表达如下:

(17)

其中,

(18)

3 直角坐标系下的FRECHET导数误差来源及修正思路

如第2节所述,(17)式提供了二维直角坐标系下立体层析所需的除旅行时对模型空间外的所有FRECHET导数的计算方法。其中传播矩阵Q中的元素必须是傍轴射线到达地表时的元素。但实际计算中存在的问题是当中心射线到达地表时射线追踪即刻停止,而这时傍轴射线往往还没有到达地表(如图2所示),使得Q矩阵元素对应的空间位置在x(t)处,而不是我们希望的x(t′)处。这个明显的误差意味着(5)式所示的FRECHET导数矩阵中的∂Sx/∂x0,∂Sx/∂z0,∂pSx/∂x0,∂pRx/∂z0,∂Rx/∂x0,∂Rz/∂z0,∂pRx/∂x0,∂pRx/∂z0将产生错误。尤其当出射到地表的中心射线出射角比较大时(即地下反射倾角较大时),这个错误将愈发严重。

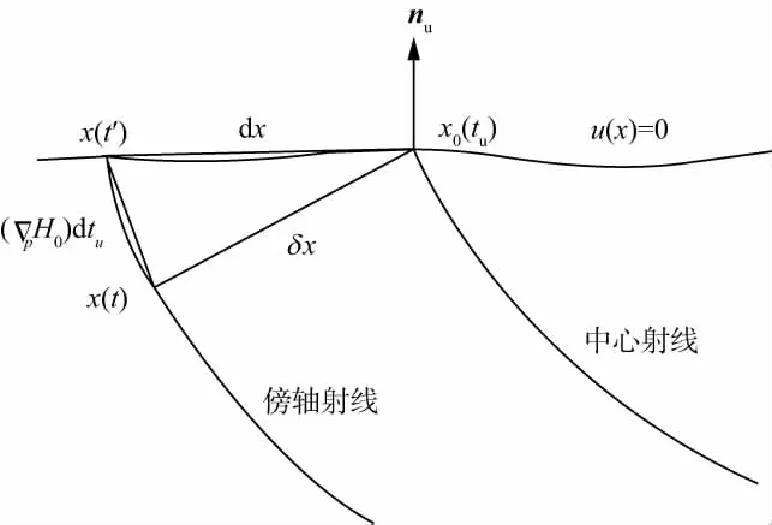
图2 直角坐标系下傍轴射线到达地表处扰动关系

针对上述问题,NAG[17]提出将中心射线再多追一小段,使得傍轴射线到达地表。但是如何计算多追这一段的积分步长dtu？这里不妨将x(t′)处的相空间表达为dy,x(t)处的相空间表达为δy,则

显然有:

(19)

这里y0代表中心射线追踪到x0时的相空间量。借助(6)式汉密尔顿形式,(19)式可进一步表示为:

(20)

(21)

由(21)式可知,只要对中心射线再追踪出dtu对应的一小段,就可以得到对应的傍轴射线到达地表的传播矩阵及出射坐标等一系列信息,再根据(17)式得到正确的FRECHET导数值。

上述过程即修正FRECHET导数计算误差的常规途径。本文根据中心射线地表出射点坐标、傍轴射线最后一点坐标以及傍轴射线最后一点与其地表预期出射点的坐标差之间存在的一个近似三角关系,直接对FRECHET导数公式进行修改,使得解决误差问题的方案更加直观简洁。

4 无需多追踪一步的修正算法

如果直接将(21)式和(17)式代入(20)式,可得:

(22)

对(22)式中x0,z0分别求导,得:

(23)

(23)式为最新的地表坐标以及射线参数p关于地下反射点坐标(x0,z0)的导数形式,相当于在没有多追踪一段的情形下,得到了正确的FRECHET导数公式。如果不做此修正,FRECHET导数直接用(17)式进行求取,结果为:

(24)

将(24)式与(23)式进行对比可以看出,没有考虑到达地表时的这一段dtu确实会带来误差。如果对(22)式中的px0,pz0分别求导,即可得到数据空间关于模型空间中散射角的导数公式,这里不再赘述其推导过程。这种修正的实质是,尽管求出了dtu,但未必要多追这一段,将其代入(20)式再对有关的模型空间分量求导也可以获得等价的结果。

在正演验证本文提出的修正方法前,这里给出本文方法与直接进行射线追踪的几何等价性证明。如图3所示,从O′点继续进行射线追踪至B点,此时对应的傍轴射线恰好达到地表O点处。

图3 中心射线与傍轴射线几何关系

容易看出x=OO′=AO′+OA,注意AB其实就是(17)式中的δz,显然有:

(25)

由地表O′点处的射线参数信息,可以求得射线出射到地表的出射角α,有:

而OA是傍轴扰动量在x方向的投影,也可以套用(17)式求得。应用上述各条件,有:

(26)

(26)式与(22)式完全一致,从另一个角度验证了本文提出的方法在几何上的正确性。

5 数值实验

5.1 傍轴射线追踪公式精度验证

如图4a所示,从地下坐标x=0,z=8000m处出射一条中心射线至地表。显然中心射线对应的傍轴射线并未到达地表,傍轴射线最后一点的位置与地表有较大的距离(图4b),若将这一点对应的扰动量当作地表接收到的扰动量,必然会影响反演的精度。

图4 中心射线及其傍轴射线(a)与射线到达地表时放大显示(b)

传统方法建议将中心射线再多追踪一段使得傍轴射线的最后一点也到达地表,以求取正确的扰动量。但根据(20)式所代表的三角关系,我们认为无须多追踪一小段射线,通过修正的FRECHET导数(即(23)式)就可以实现正确的反演。本节先通过一个简单的数值算例证明本文的修正公式能够预测出正确的地表观测扰动量。

如图4b所示,C点为中心射线到达地表时对应的傍轴射线最后一点,设E点为傍轴射线到达地表时的位置,将C点分别投影到x,z轴,得到以C点作为地表接收点扰动量与实际E点对应扰动量纵横坐标误差分别为CD,DE。在此数值算例中,DE=236m,CD=58m。

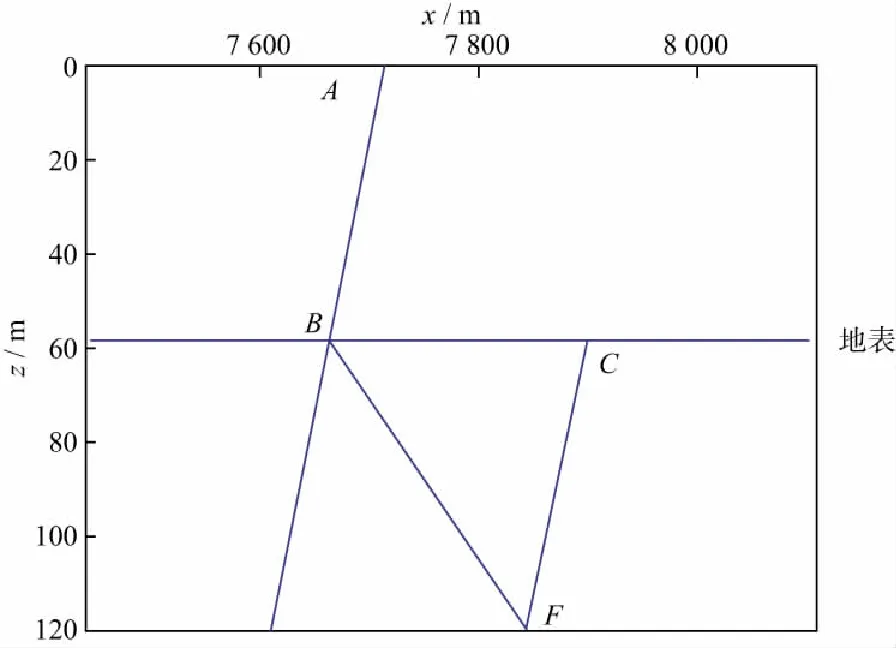
图5 对中心射线多追踪一段AB

5.2 利用修正FRECHET导数的反演精度测试

图6为采用三角剖分方式建立的常规垂直梯度多层穹隆模型。基于射线追踪正演方法获得模拟炮数据共计101炮,炮间距20m,每炮401道,道间距10m。图7a显示了某一炮对应的射线路径;图7b显示了反演所用的初始模型。

图6 多层穹隆模型

图8显示了直角坐标系下FRECHET导数未做修正时的最终反演结果,FRECHET导数利用(24)式计算得到。由图8可以明显看出,模型空间中“倾角条”(即图8中蓝色线)的反演在3～5反射层的构造翼部存在较大误差,最深部的地层产状也远未达到理想效果,迭代80次后最终的泛函残差达到e=3.4×102。

采取本文修正方法((23)式)对FRECHET导数进行修改之后,直角坐标系下的反演结果大为改进。如图9所示,对应于6个反射层的构造形态与正演模型相比非常接近,其泛函残差在10步之内即收敛到102数量级。迭代80次后最终泛函残差1.8×10,相比修正前的残差降低了一个数量级。可见本文修正方法对于直角坐标系下的立体层析而言不仅是正确的,而且是不可或缺的。

图7 基于射线追踪正演的理论数据及用于反演的初始模型a 真实速度模型及某一炮的射线路径; b 初始速度模型

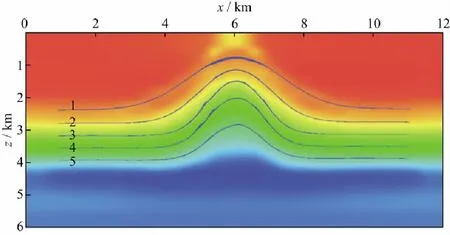
图8 应用修正前FRECHET导数的直角坐标系下第80次迭代反演结果

图9 应用本文修正方法后直角坐标系下第80次迭代反演结果

图10对比了修正FRECHET导数前后前20次迭代目标泛函的下降曲线,可以看出,修正后(蓝色虚线)第20次迭代时的目标误差泛函下降速度已明显减小,收敛速度加快。这从另一个角度说明了本文修正算法的正确性。

图10 修正FRECHET导数前后前20次迭代目标误差泛函下降速度对比

6 结束语

在直角坐标系下求取立体层析所需的FRECHET导数时,必须将傍轴射线的最后一点扰动修正至地表,否则会导致FRECHET导数求取产生误差,影响反演精度。不同于多追踪一小段中心射线以保证相应的傍轴射线到达地表的传统修正思路,本文根据中心射线地表出射点坐标、傍轴射线最后一点坐标以及傍轴射线最后一点与其地表预期出射点的坐标差之间存在的三角关系,通过一个简洁的换算获得了FRECHET导数修正公式,理论推导和数值实验证明了这个修正公式与前人提议的多追一小段射线的修正公式等价,同时也证明了这个修正是保证直角坐标系下立体层析反演精度不可或缺的环节。

[1] AL-YAHYA K.Velocity analysis by iterative profile migration[J].Geophysics,1989,54(6):718-729

[2] STORK C.Reflection tomography in the postmigrated domain[J].Geophysics,2012,77(5):680-692

[3] 邵荣峰,方伍宝,蔡杰雄,等.高斯束层析偏移速度建模方法及应用[J].石油物探,2016,55(1):91-99 SHAO R F,FANG W B,CAI J X,et al.A method of migration velocity analysis based on Gaussian beam tomography and its application[J].Geophysical Prospecting for Petroleum,2016,55(1):91-99

[4] 刘玉柱,杨积忠.有效利用初至信息的偏移距加权地震层析成像方法[J].石油物探,2014,53(1):99-115 LIU Y Z,YANG J Z.Offset-weighted seismic tomography aimed at using the first arrival efficiently[J].Geophysical Prospecting for Petroleum,2014,53(1):99-115

[5] SYMES W W.Migration velocity analysis and waveform inversion[J].Geophysical Prospecting,2008,56(6):765-790

[6] BIONDO B,ALMOMIN A.Simultaneous inversion of full data bandwidth by tomographic full-waveform inversion[J].Geophysics,2014,79(3):WA129-WA140

[7] VINCENT P,LAMBARE G,OPERTO S,et al.Building starting models for full waveform inversion from wide-aperture data by stereotomography[J].Geophysical Prospecting,2013,61(S1):109-137

[8] 倪瑶,杨锴,陈宝书.立体层析反演方法理论分析与应用测试[J].石油物探,2013,52(2):430-438 NI Y,YANG K,CHEN B S.Stereotomography inversion method theory and application testing[J].Geophysical Prospecting for Petroleum,2013,52(2):430-436

[9] REN L J,SUN X D,LI Z C.The stereotomography based on eigen-wave attributes[R].Beijing:International Geophysical Conference,2014

[10] 李振伟,杨锴,倪瑶,等.基于立体层析反演的偏移速度建模应用研究[J].石油物探,2014,53(4):444-452 LI Z W,YANG K,NI Y,et al.Migration velocity analysis with stereo-tomography[J].Geophysical Prospecting for Petroleum,2014,53 (4):444-452

[11] 王宇翔,杨锴,杨小椿,等.基于梯度平方结构张量算法的高密度二维立体层析反演[J].地球物理学报,2016,59(1):263-276 WANG Y X,YANG K,YANG X C,et al.A high-density stereo-tomography method based on the gradient square structure tensors algorithm[J].Chinese Journal of Geophysics,59(1):263-276

[12] BRILLATZ C,VIGEE L,COLEOU T,et al.Getting closer to the geology contrasts by starting stratigraphic inversion with velocity models from new tomographic methods[J].Expanded Abstracts of 84thAnnual Internat SEG Mtg,2014:4763-4767

[13] BILLETTE F,LAMBARE G.Velocity macro-model estimation from seismic reflection data by stereotomography[J].Geophysical Journal International,1998,135(2):671-690

[14] LAMBARE G.Stereotompgraphy[J].Geophysics,2008,73(5):25-34

[15] CHALARD E,PODVIN P,LAMBARE G.Estimation of velocity macro-models by 3D stereotomography[J].Expanded Abstracts of 70thAnnual Internat SEG Mtg,2000:2257-2260

[16] YANG K,XING F Y,LI Z W.3D stereotomography applied to the deep-sea data acquired in the South China Sea,part I:theoretical foundation[J].Expanded Abstracts of 86thAnnual Internat SEG Mtg,2016:4263-4267

[17] NAG S.PP/PS anisotropic stereotomography[J].Journal of Geophysics International,2010,181(1):427-452

[18] GILBERT F,BACKUS G E.Propagator matrices in elastic wave and vibration problems[J].Studia Geophysica et Geodaetica,1966,10(3):271-271

(编辑：戴春秋)

On the correction of the Frechet derivatives of stereotomography in Cartesian coordinate

ZHOU Jiaxin,XIONG Kai,YANG Kai

(SchoolofOceanandEarthScience,TongjiUniversity,Shanghai200092,China)

The Frechet derivative of stereotomography in the Cartesian coordinate system is a first-order derivative of disturbance quantity observed in surface to initial model space.If the endpoint of the paraxial ray has to be corrected to the surface,a significant error will be introduced into the Frechet derivative.The inversion accuracy will be reduced and should be modified.Differing from the conventional method to solve this problem by tracing the central ray a little longer,we use the triangular relationship among the coordinates of the emergence point for the central ray at the surface,the endpoint of the paraxial ray at the surface and the lateral difference between the endpoint of the paraxial ray and the expected emergence point at the surface,to convert a linear relationship between the endpoint coordinate difference of the central ray and paraxial ray in the surface and the initial perturbation of the ray start-point.Then the correct Frechet derivatives can be achieved based on this conversion.The method presented is exactly equivalent to the previous method with a lower computational cost.Numerical examples demonstrate the correctness and the necessity of the presented correction for stereotomography in the Cartesian coordinate system.

stereotomography,linear relationship,Frechet derivatives,Cartesian coordinate

2016-08-22;改回日期：2016-11-15。

周嘉欣(1992—),女,硕士在读,主要研究方向为立体层析反演。

杨锴(1972—),男,教授,博士生导师,主要研究方向为地震波的传播、成像与反演。

国家自然科学基金面上项目(41574098,41630964)资助。

P631

A

1000-1441(2017)04-0491-09

10.3969/j.issn.1000-1441.2017.04.004

This research is financially supported by the National Natural Science Foundation of China (Grant Nos.41274117,41574098).