基于微测井资料的双线性回归稳定Q估计

李伟娜,云美厚,2,党鹏飞,赵秋芳,2

(1.河南理工大学资源环境学院,河南焦作454000;2.中原经济区煤层(页岩)气河南省协同创新中心,河南焦作454000)

基于微测井资料的双线性回归稳定Q估计

李伟娜1,云美厚1,2,党鹏飞1,赵秋芳1,2

(1.河南理工大学资源环境学院,河南焦作454000;2.中原经济区煤层(页岩)气河南省协同创新中心,河南焦作454000)

鉴于微测井资料在近地表结构调查中的独特优势,其常用于估算近地表品质因子Q值,且以相邻道记录的谱比法应用居多。因受旅行时间拾取误差或速度估算误差等影响,Q估计结果波动剧烈、稳定性较差、估算精度较低。为此,借鉴微测井分层速度回归分析思想,提出了一种双线性回归品质因子Q估计算法。该方法利用谱比法原理,首先求取微测井各道记录相对于第一道的非相邻道谱比对数值,然后在速度分层约束的基础上采用两次线性回归求得不同层段品质因子Q值。模型试算结果表明,与常用相邻道谱比法相比,基于非相邻道的双线性回归Q估计方法明显降低了时间拾取误差和噪声干扰的影响,Q估计最大相对误差不超过25%,平均相对误差约为10%,提高了近地表Q估计的稳定性和估算精度。实测微测井数据试算结果表明,该方法可以获得与近地表速度分层相一致的较为稳定的、地质意义明确的近地表Q估计值,而且适用于不同微测井观测系统的测井数据。

微测井;线性回归;品质因子;谱比法;近地表

近地表吸收衰减补偿处理以及近地表品质因子Q值估算方法研究一直是地震勘探的研究热点之一。与深部地层介质的吸收衰减效应相比,近地表介质对地震波高频成分的吸收约占地层总吸收的80%以上[1-2]。因此,近地表衰减已成为制约地震资料分辨率的主要影响因素之一[3-4]。如何精确估算近地表吸收衰减,不仅是实现近地表衰减补偿处理的关键,同时也是提高地震资料分辨率的迫切需要。

目前,国内外关于近地表吸收衰减特性的研究主要集中在近地表衰减理论分析与实验测试[5-6]、衰减补偿处理研究[6-9]以及近地表品质因子Q值估算方法研究[10-15]等方面。就近地表衰减或品质因子Q估计而言,目前已有的方法主要包括层析成像法[10-11]、面波法[12-16]、大炮反射波与折射波法[17-20]和透射波法[4,21-26]。其中尤以透射波法(微测井或VSP观测)Q估计精度最好。JENG[21]利用单井微测井资料,基于谱比法探讨了随频率变化Q模型估算近地表Q值的可行性。石战结等[4]根据微测井记录频谱特性的变化分析了沙漠区低、降速带对地震波的衰减效应。杜增利等[22]为探究塔里木和准噶尔盆地近地表疏松沙体的衰减特性,利用微测井数据采用谱比法和上升时间法估算表层品质因子Q值,揭示了在100m深度范围内地表疏松沙体的品质因子变化范围为7～25。于承业等[23]利用双井微测井资料采用质心频移法估算近地表的Q值。云美厚等[24]以微测井速度解释成果为基础,借助Q～V经验公式进行Q值近似估算,用于对比分析川东北碳酸盐岩裸露区近地表不同岩性出露区段的衰减特性差异。张光德等[25]针对柴达木盆地三湖地区盐岩区的勘探实际,利用谱模拟谱比法由微测井数据提取近地表Q值。王宗俊[26]针对质心频移法的不足提出了基于谱模拟的质心频移Q估算方法,并利用VSP数据验证了方法的可行性。在上述方法中,不论是采用常规谱比法、谱模拟谱比法,还是采用质心频移法及其改进的谱模拟质心频移算法,主要是基于相邻道记录的频谱差异特性实现Q值估计,因此,Q估计精度受相邻道时间拾取误差、记录噪声、计算频段选取等因素的影响较大,估算结果均存在明显的Q值跳跃波动,稳定性较差。为此,在前人研究工作的基础上,本文提出了基于非相邻道的谱比法新构想,并试图通过速度分层约束和两次线性回归实现稳定Q估计。该方法有望降低时间拾取误差和噪声干扰的影响,进而提高近地表Q估计算法的稳定性和估算结果精度。

1 方法原理

单井微测井常用观测系统主要有井中激发-井口接收[4,27]和井口激发-井中接收[28]两种模式,如图1所示。一般来说,在钻井条件便利、激发条件较好的平原区大多采用第1种观测模式;在诸如山地等钻井条件困难、激发条件较差的探区,大多采用第2种观测模式。在某些特殊情况下,有时也会同时采用两种观测系统实施数据采集。为便于叙述,下面仅以井口激发-井中接收观测系统为例来阐述品质因子Q估计方法的基本原理。其对于井中激发-井口接收观测系统同样适用。

图1 微测井观测系统

1.1 相邻道谱比法Q估计方法

由图1可见,假设震源子波为a(t),任意深度hi检波器接收记录为ai(t),若仅考虑下行直达波,并假定在地震勘探频带范围内品质因子Q值无频散效应,则利用FUTTERMAN[29]吸收衰减模型,任意深度hi检波器接收记录ai(t)的振幅谱可表示为:

(1)

式中:Ai(f)为检波器接收记录振幅谱;A(f)为震源子波振幅谱;Ti为常数,表示与频率无关的衰减,包括球面扩散或透射损失等;Q为介质品质因子;V为介质速度;f为地震子波频率。

对于深度分别为hi和hi+1的任意相邻两道记录ai(t)和ai+1(t),相应振幅谱分别为Ai(f)和Ai+1(f),利用(1)式可以很容易写出谱比法Q估计表达式为:

(2)

令:

式中:Δh=hi+1-hi,为相邻道深度间隔。

(2)式可进一步改写为:

(3)

具体计算时,一般先利用(3)式通过y～f线性回归得到回归系数K,给定速度V,由(4)式即可确定Q值。

(4)

当速度无法确定时,上面各式可改写为相邻道旅行时差Δt的表达式,并通过拾取微测井相邻记录道时差来确定Q值,具体公式从略。

由(4)式可见,采用相邻道谱比法估算品质因子Q需要已知地层速度,当速度V取值精度较低时,Q估计精度受速度V的精度影响较大。若回避速度采用相邻道时差表达式来估算Q值,由于相邻道深度间隔较小,相应时差也非常小,这使得Q估计精度受旅行时间拾取精度的影响较大。换言之,采用相邻道谱比法由微测井数据估算地层品质因子对于速度取值或相邻道时差的拾取精度要求均较高。

1.2 非相邻道双线性回归Q估计方法

鉴于相邻道谱比法Q估计受速度取值或相邻道时差取值误差影响较大,为了提高算法稳定性,引入平均品质因子Qavi[30],将微测井任意深度hi的记录道ai(t)的振幅谱Ai(f)均与第1道的振幅谱A1(f)实施谱比法运算,有

(5)

式中:ti为第i道记录与第1道记录的旅行时间差;Qavi为深度为hi介质的平均品质因子。

同理,令:

则(5)式可改写为:

y=C-Kif

(6)

借鉴微测井速度解释分段拟合确定各层段速度的思想,利用速度分层实施约束,则对于同一层段各记录点的回归值Ki及相应时差ti,可以建立如下线性回归方程:

(7)

式中:Qavn为基于速度分层确定的第n(n=1,2,…)层的平均品质因子;C为截距。

(6)式和(7)式共同构成双线性回归Q估计的基本公式。具体应用中,首先从第2道开始,对于任意第i道记录,计算其与第1道的谱比对数y,利用(6)式进行y～f第一次线性回归,确定各道回归系数Ki。其次,对任意第i道相对于第1道的旅行时差ti,以速度分层实施约束,利用(7)式分段进行ti～Ki/π第2次线性回归,回归斜率即为待求近地表目的层段的平均品质因子Qavn,近似为低、降速带和高速层的层品质因子。正是由于分段回归思想的巧妙应用,避免了先求平均品质因子,再求层品质因子可能引起的误差累积。对于井中激发-井口接收观测系统,计算步骤完全一致。

1.3 振幅谱均衡处理

对于实测微测井资料,由于震源激发能量不一致(井中激发-井口接收)或检波器耦合不良(井口激发-井中接收)等因素的影响,常常会造成微测井记录各道振幅或能量不一致。因此有必要消除这种非地层吸收衰减效应造成的能量差异。振幅谱均衡处理的目的就在于此。

有两种振幅谱均衡处理方法:一是振幅谱归一化处理;二是振幅谱能量均衡处理。前者的具体做法是:首先分别求取各记录道振幅谱的最大值,然后,以振幅谱最大值的倒数作为权系数,分别对相应道不同频率振幅谱值实施加权处理。这样处理的结果是各道振幅谱峰值均趋于1。后者则是借鉴反射地震资料处理中的道间均衡处理思想,在给定频带范围内,首先计算每一道振幅谱总能量,然后,求取全部N道记录的平均能量,并以平均能量和各道总能量比值的均方根值作为权系数对各道振幅谱进行加权处理。最终使得各道振幅谱能量趋于平均能量值。

需要指出的是,振幅谱均衡处理在实现各道振幅谱能量或幅值趋于一致的同时,并未破坏原有振幅谱的形态,因而不会对Q估计结果造成影响。为了说明这一点,对于前述第i道与第1道记录的振幅谱Ai(f)和A1(f),假定均衡处理的加权系数分别为wi和w1,则加权处理后的振幅谱分别为wiAi(f)和w1A1(f)。利用谱比法原理求取能量均衡振幅谱的谱比对数可得:

(8)

令:

则(8)式可改写为:

y1=C1-Kif

(9)

对比(9)式与(6)式不难发现,两式斜率Ki未变,仅仅截距发生了变化。这说明实施振幅谱均衡处理可以在很大程度上削弱振幅差异的影响,而且利用振幅谱均衡处理结果实施双线性回归Q估计并不会造成Q估算结果失真。

2 算法精度评价

为了更好地说明双线性回归Q估计算法的稳定性和估算精度,将(7)式改写为:

(10)

显然,(10)式与(4)式形式上一致。其实际上与速度未知情形下由相邻道时间差估算Q值的计算式等价。对(10)式两端求微分,有:

(11)

由(11)式不难看出,Q估计绝对误差不仅与Ki值拟合误差有关,而且与旅行时间ti拾取误差有关。由于Ki值通常较小,所以Ki值拟合误差和旅行时间ti拾取误差将会使Q估计绝对误差成倍增大。该结论对于前述相邻道谱比法Q估计同样适用。

进一步将(11)式与(10)式相除,可得Q估计的相对误差表达式:

(12)

(12)式表明,Q估计的相对误差分别与Ki值和旅行时间相对误差成正比。换言之,Ki值拟合相对误差和旅行时间拾取相对误差越大,则Q估计相对误差也越大。

对于常用相邻道谱比法Q估计算法而言,由于道间旅行时差较小,对于相同的旅行时间拾取误差,意味着旅行时间相对误差较大,这必然使得Q估计的相对误差增大,从而降低Q估计精度。特别是,由于旅行时拾取误差使得相邻道旅行时间差ti趋于零时,将会使得算法极不稳定,难以实现Q估计。

非相邻道双线性回归Q估计算法摈弃了常用相邻道谱比法直接估算相应深度间隔Q值的做法,将相邻道旅行时间差计算扩展为非相邻道旅行时间差计算,增加了各计算道的深度间隔,在相同的时间拾取误差前提下,相对提高了非相邻道旅行时间差估算精度(即相对误差较小),因此在一定程度上降低了时间拾取误差对Q估计精度的影响。与此同时,新方法降低了出现零时差的风险,提高了Q估计算法的稳定性。此外,多点分段Q回归避免了单点计算受记录噪声、计算和拾取误差等影响,对提高Q估计的稳定性和精度同样极为有利。而且通过速度分层约束实施分段二次回归可以直接获得目的层的稳定Q估计,避免了先求平均品质因子,再求层品质因子可能引起的累积误差影响。

下面讨论Ki值拟合误差对Q估计的影响。对(6)式两端进行微分并整理可得:

(13)

(13)式表明,Ki值相对误差大小与振幅谱及频率相对误差成正比,与振幅谱对数差值大小成反比。通常,频率误差的大小主要取决于频率采样间隔的大小。频率采样间隔越小,可利用的有效振幅信息越丰富,对于Ki的准确确定越有利;反之,频率采样间隔增大,将会使得Ki值的拟合误差增大。与频率不同,当振幅谱相对误差一定时,振幅谱误差对Ki拟合精度的影响在很大程度上与振幅谱对数差值大小有关。显然,振幅谱对数差值越小,Ki拟合误差将越大。

综上所述,常用相邻道谱比法Q估计,由于道间距小,振幅谱对数差值很小,这样无疑会放大Q估计误差,进而影响Q估计精度。而采用非相邻道Q估计算法,增大了计算深度间隔,使得振幅谱对数差值加大,从而降低了振幅谱对数误差和时间拾取误差的影响,提高了Q估计算法的精度和稳定性。

3 可行性分析

为了验证非相邻道双线性回归方法的可行性,我们利用川东北镇巴探区实测微测井解释分层成果构建了相应的近地表地层模型,模型参数如表1所示。表中层速度基于微测井深度和旅行时间数据分段拟合确定;各层品质因子基于文献[24]中给出的Q～vp统计关系确定。

采用野外实际单井微测井观测系统参数,即,井口激发,激发井深h=0.5m,偏移距为1.0m。22个检波器井中接收,各检波器井下埋深分别为0.4,0.9,1.5,2.0,2.5,3.0,3.5,4.0,4.9,5.9,6.9,7.9,8.9,9.9,10.9,11.9,12.9,13.9,14.9,16.9,18.9,20.9m。假定地震子波为Ricker子波,主频为60Hz,制作含吸收衰减的合成记录,并拾取初至旅行时间,采用前述算法进行非相邻道Q估计。

表1 近地表地层模型参数

图2给出了在理想的无噪声且无时间拾取误差情形下各记录道谱比对数与频率的第一次线性回归部分关系曲线。图3为相应的道间时差ti与Ki/π的分段第二次线性回归关系曲线。由图3拾取线性回归曲线斜率,即为近地表各目的层Q值,分别为2.67,114.37和382.58。经与模型值(表1)对比分析,最大相对误差不超过3%。事实上,在这种理想情形下,采用相邻道谱比法同样可获得较为理想的Q估计,最大相对误差不超过3.5%。

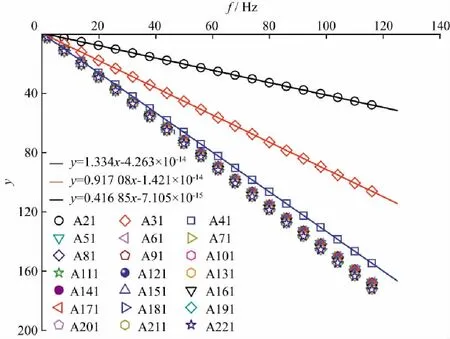
图2 谱比对数y与频率f的一次线性回归关系曲线

图3 道间时差ti与Ki/π的分段二次线性回归关系曲线

为了说明非相邻道双线性回归Q估计方法的稳定性,用实测微测井初至时间拾取值替换前述理想无时间拾取误差的旅行时间,重复前述第二次线性拟合过程,Q估计结果如图4a所示。为便于对比分析,图中同时给出了相邻道谱比法的Q估计结果(图4b)。

由图4可以看出,与常用相邻道谱比法Q估计结果相比,双线性回归法Q估计值更接近模型Q值,分别为3.14,110.04,357.86。Q估计值最大相对误差不超过25%,平均相对误差约为10%。而相邻道谱比法最大相对误差超过500%,平均相对误差约为92%。这充分说明非相邻道双线性回归Q估计算法能够显著降低初至时间拾取误差的影响,提高算法的稳定性和估算精度。

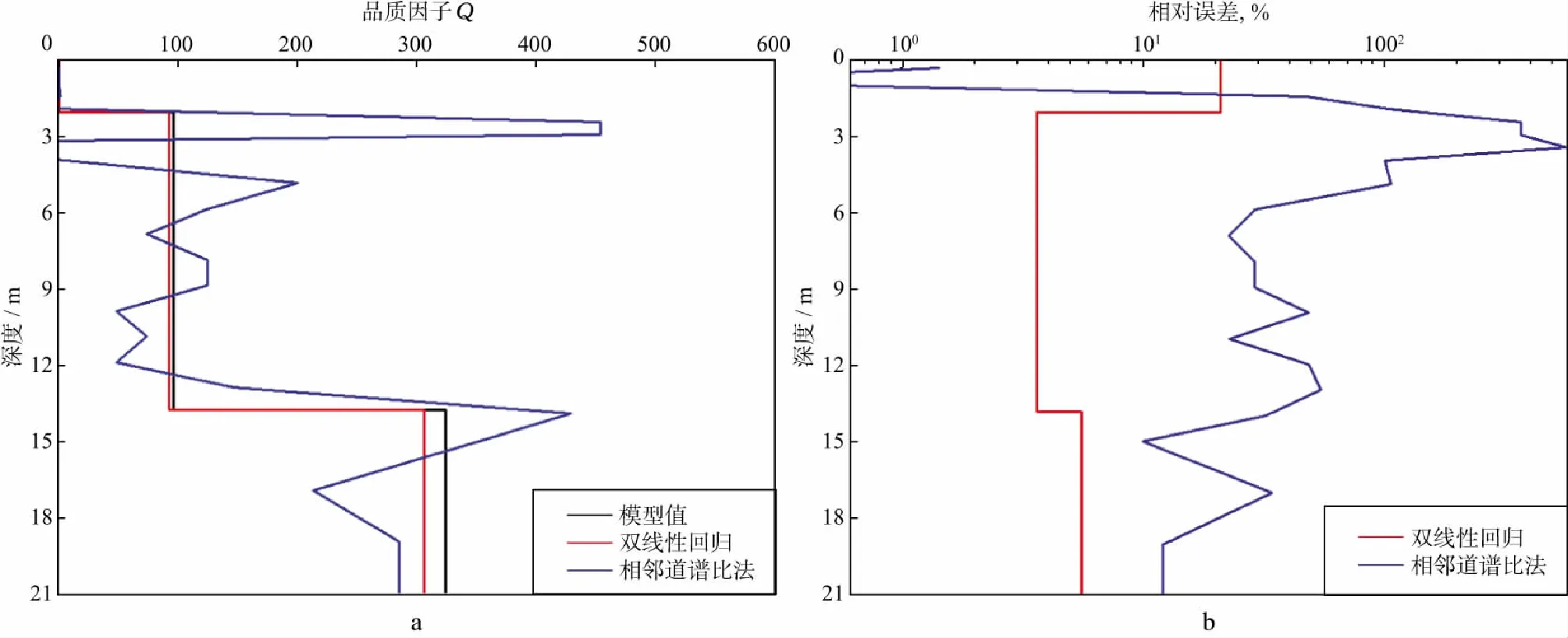
图4 非相邻道双线性回归(a)与相邻道谱比法(b)Q估计稳定性对比分析

4 应用效果分析

为了说明方法的实际应用效果,以川东北镇巴探区实测微测井数据进行应用试验。本区微测井同时进行了前述两种观测系统的数据采集。图5显示了某井井口激发-井中接收微测井原始记录剖面和相应振幅谱剖面。

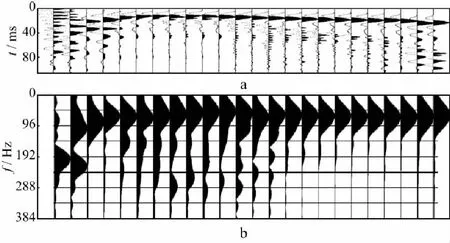
图5 井口激发-井中接收微测井记录(a)及其振幅谱(b)

鉴于实测微测井记录的复杂性,在实施品质因子Q估计计算过程中,一般需要经过滤波去噪、剔除异常道、振幅谱均衡处理和品质因子Q估计等主要步骤。具体处理流程见图6。

图6中实施滤波处理主要是为了消除高频噪声的影响,包括因检波器耦合不良(如井口激发-井中接收)引起的高频谐振等。对于那些无法利用的异常记录道(主要表现为时间域波形和频率域频谱特征双重异常)应予以剔除。实施振幅谱均衡处理的目的是为了消除因检波器耦合不良(井口激发-井中接收)或震源激发能量不一致(井中激发-井口接收)导致的记录振幅谱能量差异。由于谱比法算法的特殊性,实施振幅谱归一化均衡处理可以在很大程度上削弱振幅差异的影响,且不会造成品质因子Q估计结果的失真。与此同时,求取不同道之间旅行时差可以采用拾取记录波峰时间来实现,这样在一定程度上可以避免因初至起跳不明显而造成的时间拾取误差影响。当然旅行时差也可以采用道间互相关来确定,同样可以获得较高的拾取精度。再者,由于非相邻道谱比法基于多道统计回归来确定层段Q值,因而对道间旅行时差精度的要求比相邻道Q估计方法要小得多。

图6 非相邻道谱比对数双线性回归品质因子Q估计算法流程

图7是基于图5给出的实测单井微测井记录利用图6所示算法流程得到的近地表速度和品质因子Q估计结果(图7中v0,v1,v2,分别代表近地表低速层、降速层和高速层的速度;Q0,Q1,Q2分别代表近地表低速层、降速层和高速层的品质因子)。为便于对比分析,图中同时给出了相邻道谱比法的Q估计结果。此外,由于本井同时实施了井中激发-井口接收微测井,故图中一并展示了相应的Q估计结果。

图7 基于图5微测井数据获得的近地表速度(a)与Q值估计结果(b)

由图7b可见,与常用相邻道谱比法Q估计结果相比,基于非相邻道双线性回归Q估计结果更稳定,不存在估计值的巨大跳跃波动。而且因采用速度分层解释结果实施分段回归约束,估算Q值与近地表速度分层结果的对应关系更清晰,一致性更好,地质意义更明确,有利于进一步处理和应用。此外,对比分析井口激发-井中接收和井中激发-井口接收两种不同观测系统微测井数据的Q估计值,不难看出,除前者Q估计值略低于后者外,二者估算结果基本一致。这说明本文方法受微测井观测方式的影响较小,对不同微测井观测系统具有较好的适应性。

5 结论

1) 与目前常用的相邻道谱比法Q估计算法相比较,基于微测井非相邻道谱比对数双线性回归Q估计方法明显降低了时间拾取误差或速度估计误差等影响,Q值估计结果更稳定,平均相对误差为10%,最大相对误差不超过25%。

2) 实测微测井资料的精细处理结果表明,利用非相邻道谱比对数双线性回归Q估计方法可以获得与近地表速度分层相一致的较为稳定的Q估计值,且地质意义更明确,更有利于后续补偿处理和分析应用。

3) 当微测井记录波形稳定且频谱变化较为规律时,基于非相邻道谱比对数双线性回归Q估计方法适用于不同的微测井观测系统的数据。无论是井中激发-井口接收微测井记录还是井口激发-井中接收微测井记录均可获得较为稳定的Q值估算结果。

对于井中激发-井口接收观测系统,当不同激发点因岩性差异而导致激发子波频带存在明显差异时,如何来消除这种差异以提高Q估计的精度是今后需要进一步研究的内容。

[1] 王建民,陈树民,苏茂鑫,等.近地表高频补偿技术在三维地震勘探中的应用研究[J].地球物理学报,2007,50(6):1837-1843 WANG J M,CHEN S M,SU M X,et al.A study of the near surface high-frequency compensation technology in 3-D seismic exploration[J].Chinese Journal of Geophysics,2007,50(6):1837-1843

[2] RICE J A,CHRISTINE E K,HOUSTON L M.Shallow near-surface effects on seismic waves[J].Expanded Abstracts of 61stAnnual Internat SEG Mtg,1991:747-749

[3] ADRIANSYAH,MCMECHA G A.Effects of near-surface structure,scattering and Q on AVO measurements[J].Expanded Abstracts of 67thAnnual Internat SEG Mtg,1997:146-149

[4] 石战结,田钢.西部大沙漠区近地表地震波衰减及高频补偿技术研究[J].石油地球物理勘探,2007,42(4):392-395 SHI Z J,TIAN G.Technique of attenuation of near-surface seismic wave and high-frequency compensation in western large desert area[J].Oil Geophysical Prospecting,2007,42(4):392-395

[5] 孔令纲,傅朝奎.大地对地震信号的吸收衰减规律研究[J].油气田地面工程,2005,24(5):12-13 KONG L G,FU Z K.Study on the attenuation law of seismic signal causing by earth absorption[J].Oil-Gasfield Surface Engineering,2005,24(5):12-13

[6] 杨凯.沙漠地区低降速带地震波传播特征与衰减补偿方法研究[D].上海:同济大学,2005 YANG K.Study on seismic wave propagation characteristics and compensation method of attenuation in low velocity of desert area[D].Shanghai:Tongji University,2005

[7] 赵殿栋,郭建,王咸彬,等.沙漠区低降速带地震波的吸收补偿方法研究与应用[J].中国西部油气地质,2006,2(3):241-244 ZHAO D D,GUO J,WANG X B,et al.Study and application of absorption compensation method of seismic wave in low velocity-reducing zone of desert area[J].West China Petroleum Geosciences,2006,2(3):241-244

[8] 凌云,高军,吴琳.时频空间域球面发散与吸收补偿[J].石油地球物理勘探,2005,40(2):176-182 LING Y,GAO J,WU L.Compensation for spherical dispersion and absorption in time-frequency-space domain[J].Oil Geophysical Prospecting,2005,40(2):176-182

[9] WANG Y H.Seismic inverseQfiltering[M].Oxford:Blackwell Publishing,2008:59-79

[10] BRZOSTOWSKI M A,MCMECHAN G A.3-D tomographic imaging of near-surface seismic velocity and attenuation[J].Geophysics,1992,57(3):396-403

[11] CAVALCA M,MOORE I.Ray-based tomography forQestimation andQcompensation in complex media[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:3989-3993

[12] 刘学伟,邰圣宏,何樵登.用面波反演风化层Q值——补偿风化层吸收提高分辨率[J].石油物探,1996,35(2):89-95 LIU X W,TAI S H,HE Q D.Inversion of quality factorQfor weathered layer using surface waves compensating seismic wave absorption in weathered layer to increase resolution[J].Geophysical Prospecting for Petroleum,1996,35(2):89-95

[13] 胡家富,苏有锦.用面波估计浅土层的品质因子[J].地震学报,1999,21(4):433-438 HU J F,SU Y J.Estimation of the quality factor in shallow soil using surface waves[J].Acta Seismological Sinica,1999,21(4):433-438

[14] 裴江云,陈树民,刘振宽,等.近地表Q值求取及振幅补偿[J].地球物理学进展,2001,16(4):18-22 PEI J Y,CHEN S M,LIU Z K,et al.Near-surfaceQvalue extraction and amplitude compensation[J].Progress in Geophysics,2001,16(4):18-22

[15] XIA J H,MILLER R D,PARK C B,et al.DeterminingQof near-surface materials from Rayleigh waves[J].Journal of Applied Geophysics,2002,51(2/3/4):121-129

[16] XIA J H,XU Y X,MILLER R D,et al.Estimation of near-surface quality factors by constrained inversion of Rayleigh-wave attenuation coefficients[J].Journal of Applied Geophysics,2012,82:137-144

[17] YADARI N E,ERNST F,MULDER W.Improvement of near-surface attenuation estimation[J].Expanded Abstracts of 77thAnnual Internat SEG Mtg,2007:1242-1245

[18] YADARI N E,ERNST F,MULDER W.Near-surface attenuation estimation using wave-propagation modeling[J].Metrologia,2008,49(3):169-179

[19] 张繁昌,张汛汛,张立强,等.基于自适应子波分解的品质因子Q提取方法[J].石油物探,2016,55(1):41-48 ZHANG F C,ZHANG X X,ZHANG L Q,et al.Extraction method for quality factorQbased on adaptive wavelet decomposition[J].Geophysical Prospecting for Petroleum,2016,55(1):41-48

[20] 张显文,范廷恩,胡光义,等.基于自适应时窗的瞬时子波吸收分析技术[J].石油物探,2014,53(2):238-244 ZHANG X W,FAN T E,HU G Y,et al.Instantaneous wavelet absorption analysis technique based on adaptive time window[J].Geophysical Prospecting for Petroleum,2014,53(2):238-244

[21] JENG Y.An improved method of determining near-surfaceQ[J].Geophysics,1999,64(5):1608-1617

[22] 杜增利,施泽进,徐峰,等.近地表疏松介质吸收补偿的数学模拟研究[J].西南石油大学学报,2007,29(1):44-46 DU Z L,SHI Z J,XU F,et al.The mathematical modeling of absorption compensation in loose medium at surface[J].Journal of Sourthwest Petroleum University,2007,29(1):44-46

[23] 于承业,周志才.利用双井微测井资料估算近地表Q值[J].石油地球物理勘探,2011,46(1):89-92 YU C Y,ZHOU Z C.Estimation of near-surfaceQvalue based on the datasets of the uphole survey in double hole[J].Oil Geophysical Prospecting,2011,46(1):89-92

[24] 云美厚,曹文明,聂岩,等.碳酸盐岩裸露区近地表地震波衰减特性初探[J].石油物探,2012,51(5):425-430 YUN M H,CAO W M,NIE Y,et al.Preliminary study on the characteristics of seismic wave propagation in near surface layers of carbonate outcropped area[J].Geophysical Prospecting for Petroleum,2012,51(5):425-430

[25] 张光德,刘斌,张志林,等.柴达木盆地三湖地区盐岩区表层调查方法研究[J].石油物探,2013,52(2):195-200 ZHANG G D,LIU B,ZHANG Z L,et al.Surface investigation of salt beds in Sanhu Area,Qaidam Basin[J].Geophysical Prospecting for Petroleum,2013,52(2):195-200

[26] 王宗俊.基于谱模拟的质心法品质因子估算[J].石油物探,2015,54(4):267-273 WANG Z J.Quality factor estimation by centroid frequency shift of spectrum fitting[J].Geophysical Prospecting for Petroleum,2015,54(3):267-273

[27] 徐峰,尹成,李忠,等.井中激发地表接收的近地表结构调查方法[J].石油物探,2009,48(3):294-298 XU F,YIN C,LI Z,et al.Investigation method for near-surface structure with shot in hole and received at surface[J].Geophysical Prospecting for Petroleum,2009,48(3):294-298

[28] 张志锋,刘胜,杨继友,等.表层多波模型调查方法[J].石油物探,2012,51(3):257-263 ZHANG Z F,LIU S,YANG J Y,et al.Surface layer structure multi-wave investigation method[J].Geophysical Prospecting for Petroleum,2012,51(3):257-263

[29] FUTTERMAN W I.Dispersive body waves[J].Journal of Geophysical Research,1962,67(13):5279-5291

[30] 云美厚,聂岩,李运肖,等.地层品质因子的几种定义及相互关系[J].石油地球物理勘探,2013,48(5):816-823 YUN M H,NIE Y,LI Y X,et al.Definition and mutual relationship of several quality factors[J].Oil Geophysical Prospecting,2013,48(5):816-823

(编辑：陈 杰)

StabilityQestimation by dual linear regression based on uphole survey data

LI Weina1,YUN Meihou1,2,DANG Pengfei1,ZHAO Qiufang1,2

(1.CollegeofResources&Environment,HenanPolytechnicUniversity,Jiaozuo454000,China;2.CollaborativeInnovationCenterofCoalbedMethaneandShaleGasforCentralPlainsEconomicRegion,Jiaozuo454000,China)

At present,uphole survey data is always used to estimate the near-surface quality factorQby the adjacent trace spectral ratio method because of its unique advantages in the near-surface structure investigation.The estimatedQvalues generally show sharp jumps,poor stability and low accuracy due to the influence of travel time pickup error or velocity estimation error.Therefore,a new method for estimating quality factorQby dual linear regression is provided from a velocity regression analysis based on the uphole survey data.We first calculate the non-adjacent trace spectral ratio of the first trace of the uphole survey data using the theory of spectral ratio method;then we estimate the quality factorQfor different layers by dual linear regression under the constraint of layered results from a velocity regression analysis.Model tests show that the method called dual linear regression based on the non-adjacent trace spectral ratio method can greatly reduce the influence of travel time pickup error and noise interference compared to the conventional adjacent trace spectral ratio method and improve the stability and accuracy ofQvalue estimations.The maximum relative error of the estimationQis less than 25%,and the average relative error is about 10%.The estimation results based on real uphole survey data further show that the method can obtain more stable near-surfaceQvalues,which are consistent with near-surface velocity layering and have clear geological significance.This method has good adaptability for logging data different uphole survey systems.

uphole survey,linear regression,quality factor,spectral ratio method,near-surface

2016-11-14;改回日期：2017-04-01。

李伟娜(1989—),女,硕士在读,主要从事地震传播理论和吸收衰减反演方法研究。

河南理工大学博士基金项目(B2009-85)资助。

P631

A

1000-1441(2017)04-0483-08

10.3969/j.issn.1000-1441.2017.04.003

This research is financially supported by the Fundamental Research Funds for the Doctors at Henan Polytechnic University (Grant No.B2009-85).