一个几何引理与抛物型偏转的等效线性不动点*
2017-08-30周国全
周国全
(武汉大学物理科学与技术学院 湖北 武汉 430072)
一个几何引理与抛物型偏转的等效线性不动点*
周国全
(武汉大学物理科学与技术学院 湖北 武汉 430072)
电子在匀强电场中的电偏转与具有磁矩的原子在非均匀磁场中的运动路径的磁偏转实验——史特恩-盖拉赫(Stern-Gerlach)实验,是两个典型的抛物型偏转实验.本文论述抛物型偏转的等效不动点的存在性及其意义,并推导其统一的偏转公式.
电偏转 磁偏转 线性不动点 史特恩-盖拉赫实验 偏转公式
普通物理中的电偏转实验与量子、原子物理中的史特恩-盖拉赫(Stern-Gerlach)实验, 是物理学不同应用领域的两个性质迥异的实验[1~4].前者是实现示波器电子扫描的理论基础[1~2], 后者直接验证了原子(分子)的磁矩的空间量子化特性[3~7],从而也验证了原子(分子)角动量与其内部电子轨道取向的量子化[3~7]. 然而,撇开具体的物理背景不论, 匀强电场中电子束的偏转与非均匀磁场中原子路径的偏转却具有相似的几何规律. 它们都由场内的一段抛物线偏转外加一段切向的直线运动所构成. 本文经过对这两个实验进行具体的分析和类比描述, 尤其阐述了抛物型偏转的等效线性不动点的存在性, 归纳提炼出特有而共同的几何因子, 总结出统一的偏转公式.
1 一个几何引理
为方便展开有关抛物型偏转的线性不动点的讨论, 先证明如下数学命题以作后文引理.


(1)
或 2kx0x-y-y0=0
(1′)
(2)

(3)

图1 抛物线切线族的不动点
2 抛物型电偏转的等效不动点与偏转公式
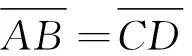
(4)
其中入射初速率v满足
(5)
由式(4)、(5)可得该电子的抛物线运动方程为
(6)
相应的参数k为
(7)

图2 电偏转的等效线性不动点

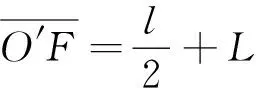
(8)
或
(9)
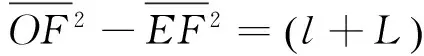
(10)
以上偏转公式(8)、(9)在忽略场的边缘效应的情况下严格成立, 不必强调“偏转板到荧光屏的距离远大于偏转板长度”而置该公式于“近似”的地位. 此外, 为了实现电偏转还必须满足出射约束条件

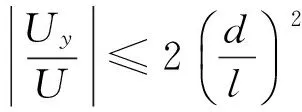
(11)
3 抛物型磁偏转的等效线性不动点——史特恩-盖拉赫实验
如图3所示,史特恩-盖拉赫实验是在非均匀横向磁场中发生原子路径的横向偏转, 它是抛物型偏转的又一典型实例, 历史上被用来证实原子轨道取向及角动量、磁矩的量子化规律.

图3 史特恩-盖拉赫实验的等效线性不动点
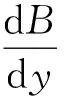
Fy=(μB)=μ
(12)
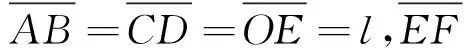
(13)
抛物线运动方程为
(14)
其抛物线参数k为
(15)
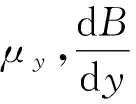
(16)
注意上式也具有空间几何因子
为保证原子在G点出射, G点的偏转距离DGy必须满足约束条件
即
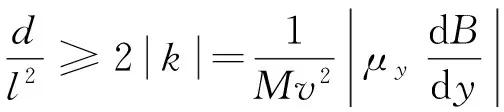
(17)
4 统一的偏转公式
综上所述, 无论是电子束在匀强电场的电偏转实验, 还是原子束在非均匀横向磁场中的史特恩-盖拉赫实验, 粒子在场域内做一段抛物线运动,在场域外做直线运动,其出射线的反向延长线必通过其初始入射方向的延长线在场域部分的中点, 就如同是从场域中点发出的射线一样, 我们称之为抛物型偏转的等效线性不动点.它的存在使问题的处理变得相当简便.另一方面, 由于两类抛物型偏转具有相同的空间几何因子,因此它们的偏转公式(9)、(16)具有相似而统一的形式
(18)

(19)
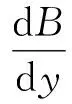
(1)忽略场的边缘效应;
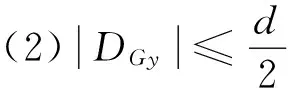
式(11)与式(17),亦即
(20)
1 林抒, 龚镇雄. 普通物理实验.北京:人民教育出版社,1981.328~332
2 周殿清.普通物理实验教程.武汉:武汉大学出版社,2005.98~104
3 褚圣麟.原子物理学.北京:高等教育出版社,1979.42~61
4 H·哈肯,H·C·沃尔夫,著.原子与量子物理学.刘歧元,译.北京:科学出版社,1993.241~243
5 郭奕玲.斯特恩-盖拉赫实验, 大学物理, 1984,3(10): 27~30
6 宁长春,汪亚平,胡海冰,等.斯特恩-盖拉赫实验历史概述.大学物理, 2016,35(3):43~49
7 吴榕生.斯特恩-盖拉赫实验中原子受力的分析.大学物理,1986(2):5~7
8 郭大钧.大学数学手册.济南:山东科学技术出版社,1985.70~73
Highlights:The existence and specific properties of the equivalent linear fixed points,for the parabolic deflection about the moving path of a point charge in a uniform electric field, and an atom with magnetic moment in a non-uniform magnetic field, were thrown light on, and a unified deflection formula was also deduced.
AGeometricLemmaandtheEquivalentLinearFixedPointofParabolicDeflection
ZhouGuoquan
(SchoolofPhysicsandTechnology,WuhanUniversity,Wuhan,Hubei430072)
parabola;electric deflection;magnetic deflection,fixed point;Stern-Gerlach experiment;deflection formula
*高等学校电动力学课程教学研究项目,项目编号:JZW-16-DD-15
周国全(1965- )男,博士,副教授,从事大学物理与理论物理教学工作, 非线性可积方程与场论研究.
2017-02-16)
