基于LabView的光纤电流互感器一体化测试系统设计

刘宪爽,肖文波,吴华明 ,肖永生,黄丽贞

(1.江西省光电检测技术工程实验室、南昌航空大学测试与光电工程学院，南昌 330063;2.南昌航空大学 信息工程学院，南昌 330063)

基于LabView的光纤电流互感器一体化测试系统设计

刘宪爽1,肖文波1,吴华明1,肖永生2,黄丽贞2

(1.江西省光电检测技术工程实验室、南昌航空大学测试与光电工程学院，南昌 330063;2.南昌航空大学 信息工程学院，南昌 330063)

光纤电流互感器日益成为电力系统中最重要的设备，在实用化研究中，光纤电流互感器的检测精度是重要的指标之一，而被测电流的谐波和光纤电流互感器内部的噪声往往影响其测量的准确性;因此对光纤电流互感器谐波的检测以及对其解调算法实用性的验证非常重要;为进一步的谐波治理提供依据及验证解调算法能否有效运用问题，在详细分析现有的谐波检测理论和两种解调算法原理的基础上，设计了一种基于虚拟仪器LabView的光纤电流互感器谐波检测及解调算法测试一体化系统，在快速检测电流各次谐波电平的同时解调出被测电流的信息并对比验证两种解调算法的可行性与优越性，验证结果表明第二种解调算法的精度明显优越于第一种解调算法，更能适用于光纤电流互感器的信号解调。

光纤电流互感器; 谐波检测; 解调算法验证; 一体化系统; 虚拟仪器

0 引言

光纤电流互感器(fiber-optical current transformer，FOCT)因其结构简单、绝缘性能好、无铁磁饱和、动态范围广等优点，正逐步取代传统电磁式电流互感器，成为电器设备行业设计的主流。光纤电流互感器在结构和材料满足最佳的条件下其性能的优劣程度主要取决于其解调算法的优越性与实用性。因FOCT的被测电流信号在50Hz及10次以下谐波的离散频率点，谐波会引起FOCT在测量暂态电流时发生比较大的畸变，且谐波含量的大小直接影响供电、用电系统设备的安全[1]。因此对FOCT被测电流信号谐波的检测具有非常重要的意义。目前，国内对光纤电流互感器的研究大多是对其光路结构和光学材料的改进，缺乏对解调算法的研究与验证[2]。到目前为止，据我们所知谐波检测与解调算法测试的一体化系统很少见诸报道。据此，本文基于LabView开发平台，设计了一套光纤电流互感器谐波检测与解调算法测试的一体化平台，在验证对比两种光纤电流互感器新型解调算法的可行性与优越性的同时对其被测电流的谐波进行检测，为进一步的谐波治理以及解调算法的实际应用提供依据。

1 FOCT解调算法与谐波检测原理

1.1 FOCT基本原理

图1为基于Sagnic反射式全光纤电流互感器原理图。其中，光电探测器接收到的信号经过信号调理之后输入到信号处理单元，经解调、数字控制之后加到相位调制器解调，使之产生与电流导致的Faraday相移大小相等、方向相反的反馈补偿相移，通过测量该反馈补偿相移的大小，就可以获取FOCT被测电流的信息[3]。

图1 基于Sagnic反射式全光纤电流互感器系统结构图

图1中光电探测器输出的信号I为：

I=KI0[1+cos(Φs)]

(1)

其中:I0是初始光强，Φs是相移。

当带有被测电流信息的光信号经过光电探测器转换成电信号时，由于信号远小于光电探测器内部噪声，故很容易淹没在噪声中，所以需要解调算法进行信号提取[4]。

1.2 解调算法原理

假设调制频率为fm，则由相位调制器引起的相位差为：

ΔΦm(t)=a*cos(2πfmt)

(2)

其中:a为调制深度。

那么式(1)可以写为:

I=KI0{1+cos[Φs+ΔΦm(t)]}

(3)

由被测电流引起的相干光的相位差为：

Φs=Asin(2πfct)

(4)

式中，fc为被测电流的频率。

将式(4)代入式(3)有：

I=KI0{1+cos[Asin(2πfct)+a*cos(2πfmt)]}

(5)

对上式进行分解，然后按照第一类Bessel函数展开，可以得到：

I=KI0{1+cosΦs[J0(a)-2J2(a)cos(4πfmt)+

2J4(a)cos(8πfmt)-…]-sinΦs[2J1(a)cos(2πfmt)-

2J3(a)cos(6πfmt)+…]}

(6)

式中，Jn(x)为n阶第一类Bessel函数。

上式可表示为调制信号多次谐波的叠加，若测量出基波信号的幅值V1，则根据：

V1=-2KI0J1(a)sinΦs

(7)

即可计算出Φs，而Φs反映的就是当前被测电流的值。进而从上式可得：

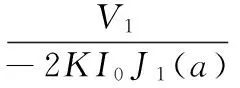
(8)

显然，上式结果与光强I0和调制深度a有关，而干涉光强和调制深度均随外界环境的变化而缓慢变化，导致测量的误差比较大。

以上算法，我们把它称之为第一种解调算法。

文献[5]提出的算法消除了干涉光强和调制深度对测量结果的影响。

对被测电流信号中的基波、二次谐波和四次谐波的进行处理，即：

V1=-2KI0J1(a)sinΦs

V2=-2KI0J2(a)cosΦs

V4=2KI0J4(a)cosΦs

(9)

对上式进行相除运算有：

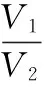
(10)

从而可得被测电流引起的相位差Φs：

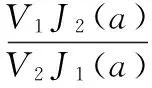
(11)

又因Φs=4VNI(V是韦德尔常数，N是光纤电流匝数，I是被测电流)，这样就可以得到被测电流I。

我们将这种算法称之为第二种解调算法。

恶性病变共有10例，主要分布在胸部与腹部，CT检查显示病灶区域密度不均匀，有点状钙化病灶存在，病变周围组织出现受压，增强扫描检查显示病灶区域有不均匀强化。MRI检查显示颈部为T1WI、T2WI高信号，增强扫描不存在强化。

1.3 谐波检测原理

LabView提供了很多FFT快速谐波检测的函数，但简单利用FFT进行谐波分析时存在频谱泄露和栅栏效应现象，检测的准确度不高[6]。针对FFT算法的不足，国内外学者提出了将矩形窗、Hanning窗、Blackman-Harris窗、Nuttall窗等运用到FFT谐波分析中，这些算法的共同处理方法是使窗函数旁瓣幅值尽可能小且衰减速度尽可能快，但是这些算法在提高谐波分析精度的同时也增加了算法的复杂度。另外，信号的动态分析效果也会受到窗函数固定性能的制约。本文的一体化测试系统设计了一组可调的窗函数，可以充分对比所加各种窗函数的谐波检测精度，根据信号的性质，灵活的选择窗函数。

2 一体化测试系统设计

根据以上原理，我们设计了基于LabView的一体化测试系统，该系统由3个模块组成，即仿真信号设置模块、谐波检测模块和解调测试模块。

2.1 仿真信号设置模块

该模块主要作用是模拟光纤电流互感器的输出信号，其中，谐波检测模块仿真的输出信号由被测电流基波及10次以下谐波和白噪声叠加而成，其中噪声可以设置为Uniform、Gaussian、Periodic和inverse f等类型。因FOCT输出数据中包含了探测器散粒噪声、光源相对强度噪声、电路噪声和环境噪声，这些噪声是时变的，相互耦合且没有准确的统计特性[7]。故简单的叠加白噪声信号不能严格的验证解调算法的有效性，本文根据FOCT实际工作的噪声特性编写了功率谱密度函数不平坦的有色噪声子程序，再叠加基波及10次以下谐波和白噪声，组成解调测试模块FOCT的仿真信号，从中解调出被测电流的幅值和相位信息。

2.2 谐波检测模块

该模块我们可以设置窗函数的类型，包括矩形窗、Hanning窗、Kaiser窗、高斯窗、Blackman窗、4阶B-Harris窗等。通过对比来分析每种窗函数下的谐波检测精度。图2为该模块对应的前面板。

图2 谐波检测模块前面板

该模块主要完成谐波失真分析，包括测定基波和所有谐波的幅值电平，返回基波频率以及总的谐波失真度(THD)。我们可以在该前面板中观察FFT变换后的频谱、检测的信号波形、检测的信号频谱以及谐波失真度和谐波含有率等信息。

(12)

式中，U1为基波电压有效值，U2，U3，…，Un为各次谐波分量的电压有效值。程序中还通过下式可求出了各次谐波电压含有率(HRUn):

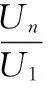
(13)

式中，U1为基波电压有效值，，Un为第n次谐波电压有效值。

2.3 解调测试模块

在图2的前面板中点击“解调测试”选项，就可以对“传感光纤匝数N”、“线圈匝数H”和“韦德尔常数V”等常用参数进行设定，通过对这几个参数的设定和调整，我们可以得出最佳的测试效果。

通过该模块我们验证对比上述两种解调算法的有效性和准确度。下面将对这两种解调算法的设计思路简要说明如下。

首先对仿真信号进行FFT变换，提取变换后的一、二、三、四谐波进行比值运算处理，然后将所有运算结果存储到Excel中。第一种解调算法通过设置常用参数的值和评估J2/J1的值，经过数学运算得到被测信号基波的幅值和相位；第二种解调算法利用程序调用存放在Excel表格上的数据进行处理，再根据预设的子数组(常数值、阈值)进行方程运算得出调制深度，然后再根据返回的调制深度和J2/J1的值进行贝塞尔函数展开，再作数学运算处理，这样就得到被测电流基波的幅值和相位。另外，存放在EXCEL中的数据也可用于测试数据的纪录和回放。

第二种解调算法程序数学运算过程如下：

Φs=4NVI

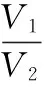
通过以上两式得到被测电流I：

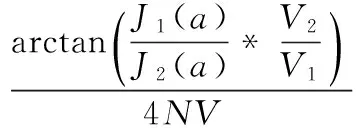
式中，N代表光纤匝数；V代表韦德尔常数；Φs为被测电流引起的相干光的相位差；V1和V2分别代表基波和二次谐波的幅值；J1(a)和J2(a)分别为第一阶贝塞尔函数和第二阶贝塞尔函数。

3 仿真结果分析

根据FOCT测量的电流信息，考虑到第10次谐波。本文设置的仿真信号如表1所示。

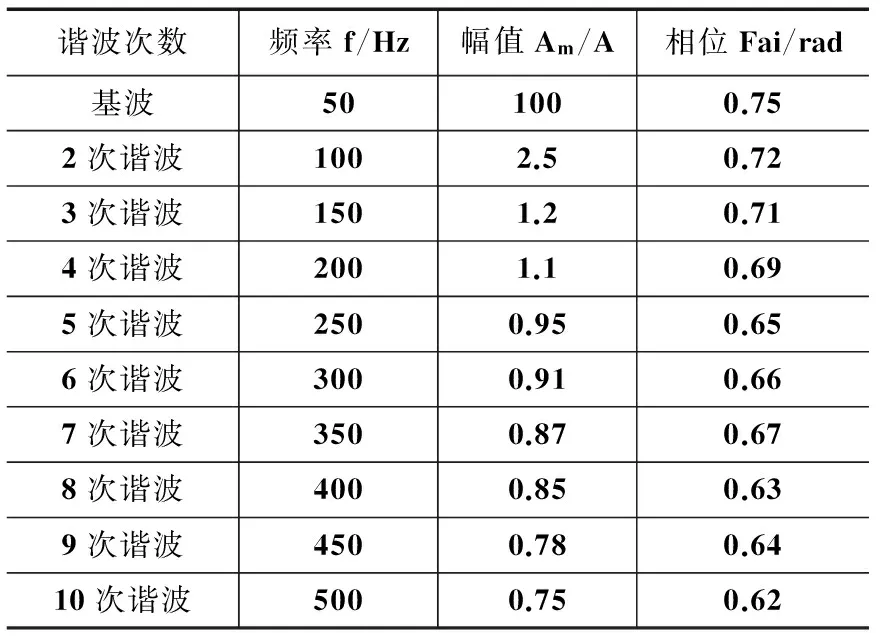
表1 仿真信号的基波和谐波成分

根据采样定理，通过前面板将采样频率设为1 000 Hz，采样点数为500点。

3.1 谐波检测结果分析

对于谐波检测模块，选择3种不同的窗函数(矩形窗、Hanning窗、Blackman窗和Kaiser窗)，得到各次谐波电平的测量结果如表2所示。

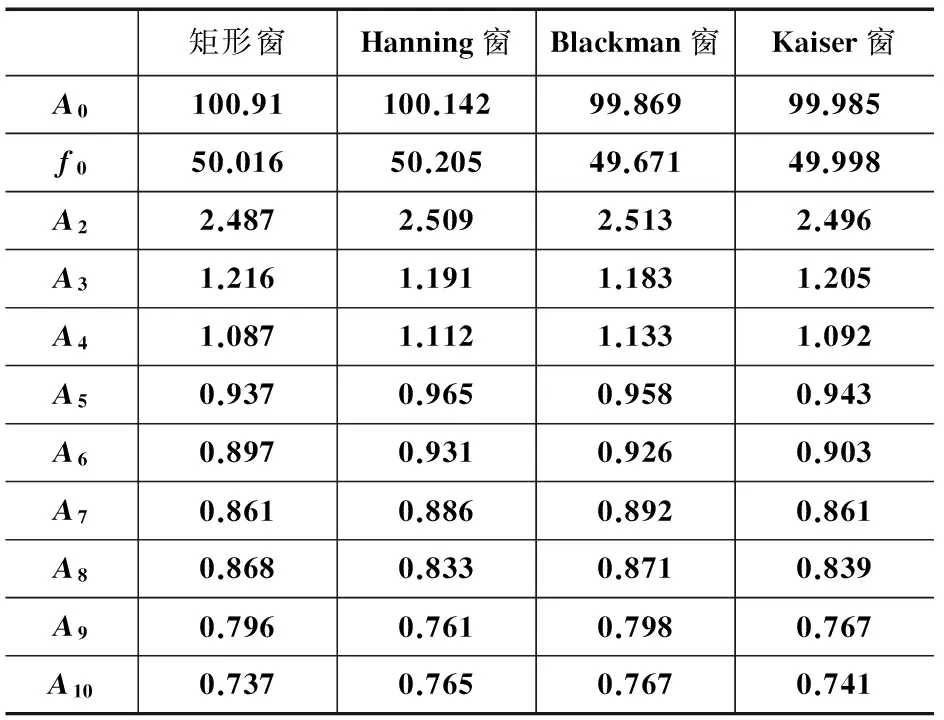
表2 不同窗函数下谐波检测结果对比

表2中，An(n=0,2,…,10)，代表各次谐波幅值，f0表示基波频率。由表2中的数据可知，基于Kaiser窗的FFT算法检测精度更高，这说明相比与矩形窗、Hanning窗和Blackman窗，Kaiser窗更能抑制频谱泄露。因此本文对仿真信号选择加Kaiser窗的FFT算法对光纤电流互感器进行谐波检测。

噪声存在时，信号谐波分量间泄露量会发生变化，影响信号谐波参数估计的准确性[8]。本文对在高斯白噪声和均匀白噪声两种噪声类型的影响下的谐波参数进行仿真实验。两种噪声影响下的基波幅值的相对误差分布曲线如图3所示。

图3 两种噪声类型影响下基波幅值相对误差

由图3可知，两种类型的白噪声影响下的基波幅值相对误差都随着噪声强度的增大而增大。我们由此得出的结论是噪声的强度对光纤电流互感器的谐波检测的参数影响很大，所以在谐波检测时必须要考虑到噪声的影响。

下面对本系统检测的各次谐波电平进行分析。将噪声设置为均匀白噪声，幅值为5.5。对各次谐波取10次计算结果进行分析，得到各次谐波电平相对误差如图4所示。

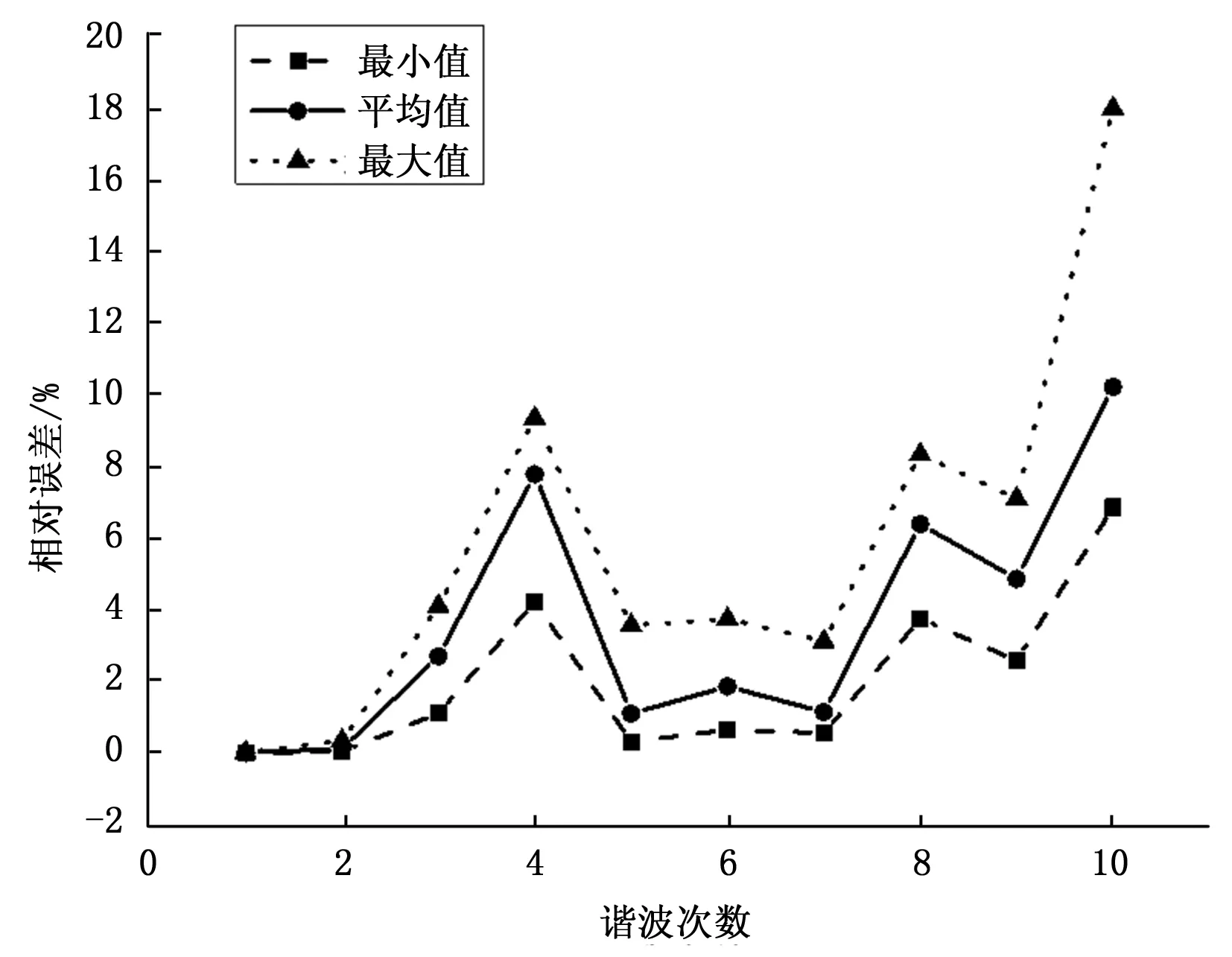
图4 各次谐波的相对误差

从图4中可以看出，各次谐波10次相对误差计算结果的最大值在20%以内，平均值在10%以内，表明本文设计的谐波检测算法在噪声的影响下能快速检测到各次谐波电平且准确度也能满足光纤电流互感器谐波检测的要求。

3.2 解调算法测试结果分析

通过多次试验，将传感光纤匝数N、线圈匝数H和韦德尔常数V分别设置为10、180和0.105时可达到最佳测试效果。第一种解调算法J2/J1的结果设定为0.02。取10次计算结果，解调出的基波电流幅值和相位角分别如表3和表4所示。

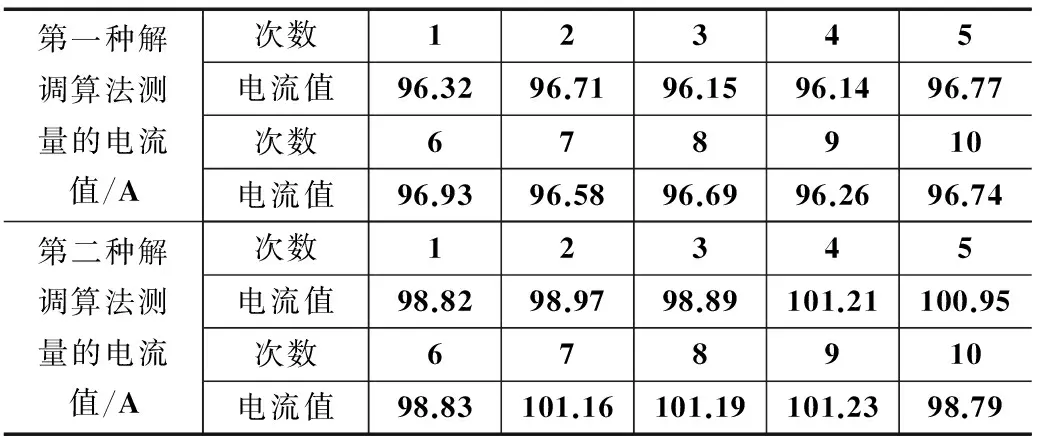
表3 两种解调算法解调出电流幅值10次结果

从表3中的数据可知，第一种解调算法测量的电流值的10次结果相对误差的平均值为3.47%；第二种解调算法测量的电流值的10次结果相对误差的平均值为1.14%。因此可以得出结论，第二种解调算法解调出的电流值的准确度要明显优于第一种解调算法。

表4 两种解调算法解调出电流相位角10次结果

从表4中的数据可知，第一种解调算法测量的相位角10次结果相对误差的平均值为7.74%；第二种解调算法测量的相位角10次结果相对误差的平均值为2.53%。所以，第二种解调算法解调出的相位角的准确度要明显优于第一种解调算法。

由此我们可以得出结论：第二种解调算法的性能要优于第一种解调算法。因为第二种解调算法消除了光强I0和调制深度a的影响，因此解调算法精度更高，这与理论推导相符。

4 结论

本文详细介绍了反射式全光纤电流互感器的基本原理、两种解调算法的原理和谐波检测方法。通过基于LabView的平台，设计了基于LabView的FOCT的谐波检测及验证两种解调算法有效性的一体化测试系统。通过对结果分析，我们可知，该系统能够在同一个电流情况下进行谐波检测以及对两种解调算法进行对比验证，并将有关数据自动存入Excel表格。通过本文设计的谐波检测方法，可以较快速较准确的获得FOCT被测电流信号各次谐波的幅值、基频、谐波失真度以及谐波含有率等信息，为进一步的谐波治理提供了理论依据。通过对两种解调算法的比较，能够验证第一种解调算法受干涉光强和调制深度影响较大，故其解调的电流幅值和相位角的相对误差比较大；而第二种解调算法可以有效消除干涉光强和调制深度对测量结果的影响，其准确度与可靠性明显提高。本文的测试系统为FOCT的测量精度提供了参考方案。

[1] 谢井华,龚仁喜,宁存岱.基于虚拟仪器的谐波检测及远程传输实现[J].电测与仪表,2010,47(531)：47-51.

[2] 欧阳康,洪小斌,伍 剑,等.全光纤电流互感器的新型调制解调方案研究[J].中国激光,2015,42(1)：0105004-1-6.

[3] 张 健,及洪泉,远振海,等.光学电流互感器及其应用评述[J].高电压技术,2007,33(5)：32-36.

[4] 黄建华,王 佳.光学电流互感器的关键技术[J]. 电力自动化设备,2009,29(12)：94-97.

[5] 裴焕斗,祖 静,陈 鸿.全光纤电流互感器研究[J].电子测量与仪器学报,2008,22(4)：34-38.

[6] 唐俊龙,陈连举,文勇军.基于虚拟仪器技术的电力谐波失真分析[J].电测与仪表,2010,47(531)：42-46.

[7] 王立辉,伍雪峰,孙 建,等.光纤电流互感器噪声特征及建模方法研究[J].电力系统保护与控制,2011,39(1)：62-66.

[8] 高云鹏,滕召胜,卿柏元.基于Kaiser窗双谱线插值FFT的谐波分析方法[J].仪器仪表学报,2010,31(2)：287-292.

Design of Integrated Testing System for Optical Fiber Current Transformer Based on LabView

Liu Xianshuang1, Xiao Wenbo1, Wu Huaming1，Xiao Yongsheng2, Huang Lizhen2

(1.Jiangxi Engineering Laboratory for Optoelectronics Testing Technology, School of Measuring and Optical Engineering, Nanchang Hangkong University, Nanchang 330063，China; 2.School of Information Engineering, Nanchang Hangkong University, Nanchang 330063，China)

Optical fiber current transformer has become one of the most important equipment in power system, in the practical research, the detection accuracy of optical fiber current transformer is one of the important indexes, and the accuracy of the measured noise and internal harmonic optical fiber current transformer current often affecting the measurement. So it is very important to detect the harmonic of the optical fiber current transformer and to verify the practicability of the demodulation algorithm. Based on the detailed analysis of the existing harmonic detection theory and two kinds of demodulation algorithm, we design a detection and demodulation algorithm of optical fiber current transformer harmonic test system based on LabView integration, in the rapid detection of harmonic current and harmonic distortion level at the same time the demodulated information and comparing the measured current to verify the feasibility and superiority of two demodulation algorithm, the verification results show that the second kinds of demodulation algorithm accuracy is superior to the first demodulation algorithm, more suitable for signal demodulation of fiber optic current transformer.

fiber-optical current transformer; LabView; demodulation algorithm; harmonic detection; integrated system

2016-12-29；

2017-02-06。

国家自然科学基金(11264031)；江西省青年科学基金重大项目(20143ACB21011)。

刘宪爽(1990-)，男，山东人，硕士研究生，主要从事光纤电流互感器的信号处理方向的研究。

吴华明(1975-)，男，江西人，博士，讲师，主要从事微纳光电器件设计及光纤传感及材料分析计算方向的研究。

1671-4598(2017)07-0039-04

10.16526/j.cnki.11-4762/tp.2017.07.010

TH7

A