基于梯度型最小二乘滤波的船摇隔离度测试研究
2017-08-30蔡浩
蔡 浩
(中国卫星海上测控部,江苏 江阴 214431)
基于梯度型最小二乘滤波的船摇隔离度测试研究
蔡 浩
(中国卫星海上测控部,江苏 江阴 214431)
针对传统船摇隔离度测试方法效率低、误差大、操作复杂、且不能有效解决扰动跳变的不足,对船摇隔离的基本原理进行了分析,建立了梯度型最小二乘滤波模型,提出了基于梯度型最小二乘滤波算法对测量数据进行滤波处理,利用VC++编程实现对船摇隔离度的自动化测试,并在船舶生摇的条件下进行船摇隔离度的测试分析;对比传统方法测试结果表明,该方法能有效滤除测量数据中的随机误差,较大程度地降低了扰动跳变的抖动量,提高了伺服系统船摇隔离度的测试精度。
梯度下降;最小二乘滤波;船摇隔离度;自动化测试
0 引言
船摇隔离度是衡量船载雷达伺服系统抵消船摇扰动、稳定天线波束指向能力的关键指标,为了满足系统设计需求,需在船舶生摇的动态条件下进行隔离度测试。当前船摇隔离度的计算主要包括人工挑点计算和自动化软件测试两种方法[1],人工计算方法[2]是通过记录查找角度和误差电压等数据,折算出与之相应的角度变化量或误差电压对应的角度残差,然后按照船摇隔离度公式计算得到各项隔离度,这种方式计算量大、时间长,且随操作者经验不同易产生相应的误差;自动化软件测试中常用的滤波算法主要是加权平均滤波法和最大似然参数估计法[3],已经难以满足总体对船摇处理的精度和实时性要求[4],对外来扰动引起测角数据及误差电压抖动跳变的滤波效果不明显,影响船摇隔离度的测试精度。梯度型最小二乘滤波算法是从实时测量数据中剔除信号中夹杂的误差噪声信号,它实际是对连续变化函数估计的一种最小二乘逼近。本文通过分析船摇隔离的基本原理,基于梯度型最小二乘滤波算法对测量数据进行滤波处理,利用VC++软件编程实现对船摇隔离度的自动测试,以达到减小随机误差、降低扰动跳变的抖动量,准确测试船摇隔离度的目的。
1 船摇隔离结构及原理
目前,船载雷达伺服系统主要利用伺服闭环稳定、速率陀螺反馈稳定[5]和前馈补偿稳定3种方法隔离船摇,实现天线稳定跟踪。船摇隔离结构方框图[6]如图1所示:
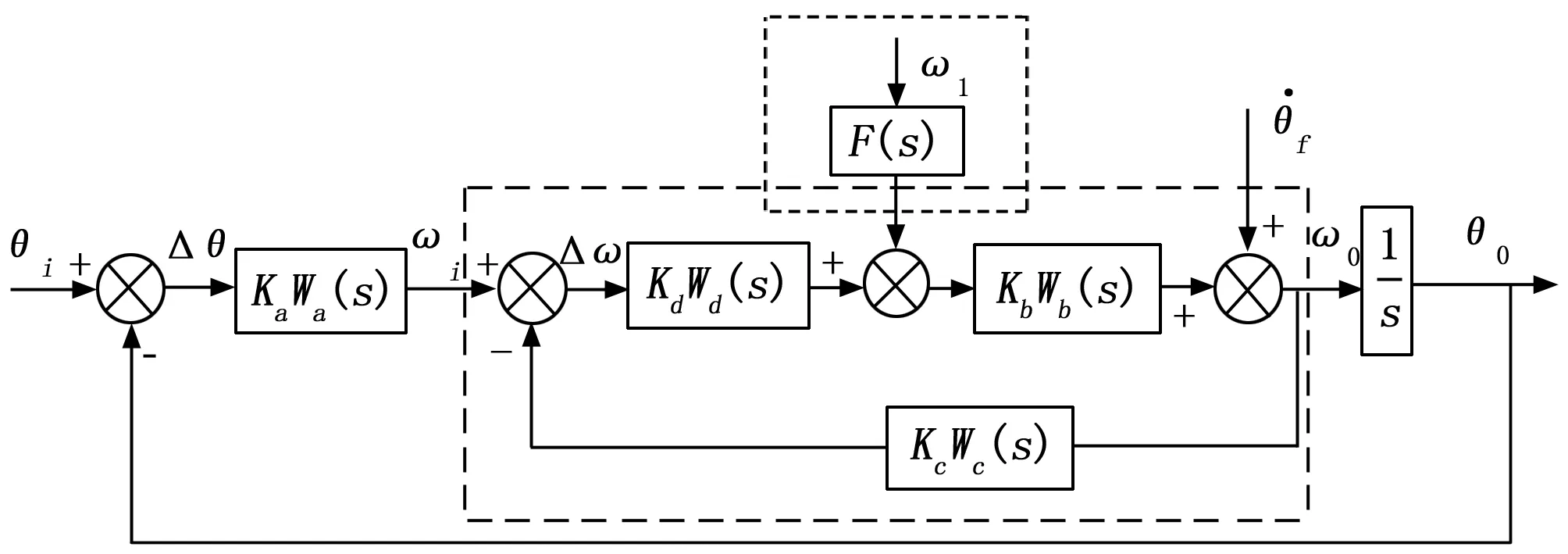
图1 船摇隔离结构图
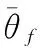
船摇隔离的基本原理主要由三部分组成:速率陀螺稳定环、自跟踪位置环和前馈补偿。上虚线框处,通过船摇速度前馈补偿,将敏感的船摇速度信号以相反的方向加入速度环路输入端,达到隔离船摇扰动的目的。下虚线框内,为速率陀螺稳定环[7],船摇产生的角速度被陀螺所敏感负反馈给回路,通过主回路使天线朝着与船摇扰动相反的方向运动,以陀螺信号反馈闭环稳定实现隔离船摇扰动。框图的最外环为自跟踪位置环,其角误差测量通过天线馈源和跟踪接收机共同实现,跟踪接收机鉴相器输出电压大小与电轴和目标间的相对偏角变化一致,自跟踪位置环路的作用是使输出量θ0随动输入量θi,并且克服船摇引起电轴偏离目标的扰动,实时控制天线向误差减小的方向运动实现天线自动跟踪目标,起到隔离船摇的作用。采用上述3种隔离船摇的方法可获得较高的船摇隔离度[8],如果在跟踪过程中突然接收机失锁,自跟踪环路开路,天线不会立即飞车,仍能指向目标保持记忆跟踪,但由于陀螺干扰力矩产生惯性空间漂移,不能长时间工作在这种方式跟踪目标。
2 梯度型最小二乘滤波模型
在实际应用中,误差电压和测角数据中均存在随机噪声及外来扰动可能产生的较大幅度的抖动[9],给船摇隔离度的计算带来较大影响。为了提高船摇隔离度的计算精度,实现计算机自动进行数据处理,需要实时滤除数据中的随机噪声分量和外来扰动引起的抖动,这里采用梯度型最小二乘滤波算法对误差电压进行滤波,然后由计算机自动选取峰峰值进行船摇隔离度的计算。最小二乘法[10]由法国数学家高斯提出,是一种具有大平坦幅度响应、应用广泛的估计方法。梯度型最小二乘滤波算法的基本思想是使测量数据和估计值之间差值的平方最小,在前一次估计结果的基础上,利用新引入的观测值根据算法对前次估计的结果进行修正,从而得出新的估计值,并与前次估计结果进行比较,若达到设置的差值上限则溢出,同时用前次估计结果替换新的估计值,这样,随着新的观测值的逐次引入,一次接一次的进行状态估计,直到达到满意的精度程度为止,梯度型最小二乘滤波算法的模型[11]如下:

基于最小二乘准则[12],设遗忘因子λ(0<λ≤1),方位、俯仰误差电压系数Kxt、Kyt要使滤波后误差的加权平方和分别达到最小,则:
(1)
(2)
以方位误差电压滤波计算为例,俯仰误差电压滤波可类推,用向量求模形式表示为:
(3)
其中:
(4)
(5)
(6)
Qxt对Kxt求梯度,
(7)
设滤波步长γt,根据梯度下降准则,函数沿着梯度相反的方向-▽t下降最快,最优步长由曲线性搜索算法确定,t+1时刻系数满足:
Kx(t+1)=Kxt-▽t·γt
(8)
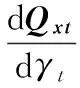
将Kx(t+1)代入Qxt替换其中的Kxt,求导化简得:
(9)
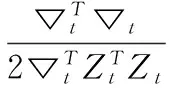
(10)
利用MATLAB的M语言可快速编程实现数字滤波,而VC++可自动调用MATLAB程序,方便了程序的设计。
部分MATLAB函数实现程序如下:
steepest m;
function [kender]=steepest(Qxt,a,e) %梯度下降法,Qxt为目标函数,a为初始点,e为终止误差,k表示迭代次数,ender表示最优点:
symsKxtγtm;
d=-[diff(Qxt,Kxt),diff(Qxt,γt)]; %分别求Kxt和γt的偏导数,即下降的方向
flag=1; %循环标志
k=0;
while(flag)
d_temp=subs(d,Kxt,a(1)); %将初始点代入,求本次下降Kxt梯度值
d_temp=subs(d_temp,γt, a(2)); %将初始点代入,求得本次下降γt梯度值
d_temp=double(d_temp);
nor=norm(d_temp); %范数
if(nor>=e)
a_temp= a+m*d_temp; %改变初始点a的值
Qxt_temp=subs(Qxt,Kxt,a_temp(1)); %将改变后的Kxt和γt代入目标函数
Qxt_temp=subs(Qxt_temp,γt,a_temp(2));
h=diff(Qxt_temp,m);
m_temp=solve(h); %求方程,得到本次m
a=a+m_temp*d_temp; %更新起始点
k=k+1;
else
flag=0;
end
end
ender=double(a); %终点
end
采用船摇隔离度测试的实测数据作为仿真数据,利用本文设计的梯度型最小二乘滤波算法对数据分别进行滤波处理,以跟踪位置回路(自跟踪+陀2+船馈)隔离度为例,处理前后的方位、俯仰误差电压波形图及局部放大图如图2~图4所示。

图2 滤波前后方位误差电压波形图

图3 滤波前后俯仰误差电压波形图


图4 滤波前后方位误差电压局部放大图
比较方位、俯仰误差电压滤波前后曲线可以看出,由于船摇扰动的影响,误差电压中叠加了高频噪声分量,采用梯度型最小二乘滤波后,误差电压的变化规律没有改变,滤波结果与滤波前数据的重合性较好,而噪声明显减小,抖动量在滤波之后得到了明显降低,有效减小了随机误差,提高了船摇隔离的测试精度,达到了预期效果。
滤波前后数据统计量比对结果如表1所示。

表1 误差电压原始数据与滤波输出统计量对比
由表1可以看出,通过滤波,数据的均值较接近,同时标准差有了明显减小,说明梯度型最小二乘滤波算法可以直接对误差电压数据进行处理,并且有效抑制了随机误差,减小了抖动量。多组数据滤波处理分析表明,该滤波算法对船摇隔离数据处理是适用的。
3 船摇隔离度自动测试软件的实现
基于梯度型最小二乘滤波模型的船摇隔离度自动测试软件采用面向对象的VC++编程实现对船摇隔离度的自动测试。根据船摇隔离度的定义及设备不同环路指标要求[13],主要设计了大地手控隔离度、自跟踪位置回路隔离度、陀螺回路隔离度、船摇前馈回路隔离度及总隔离度5类测试项目。每种隔离度测试项目在方位支路和俯仰支路上分别进行,如图5所示。

图5 船摇隔离度参数设置
在软件编程上采用分步处理的方法,包括船摇隔离度参数设置(参数设置界面如上图所示)、数据采样、梯度型最小二乘滤波和挑点计算输出四部分,根据船摇隔离度计算方法,程序中设置采集满足船舶生摇幅度的5个船摇周期内的相关数据,并统计每个船摇周期内误差电压及角度数据的极值点(一个周期内的波峰和波谷值)存贮在相应的变量中。按照隔离度计算公式即可实时计算出船摇隔离度并在软件界面显示,软件流程图如图6所示。
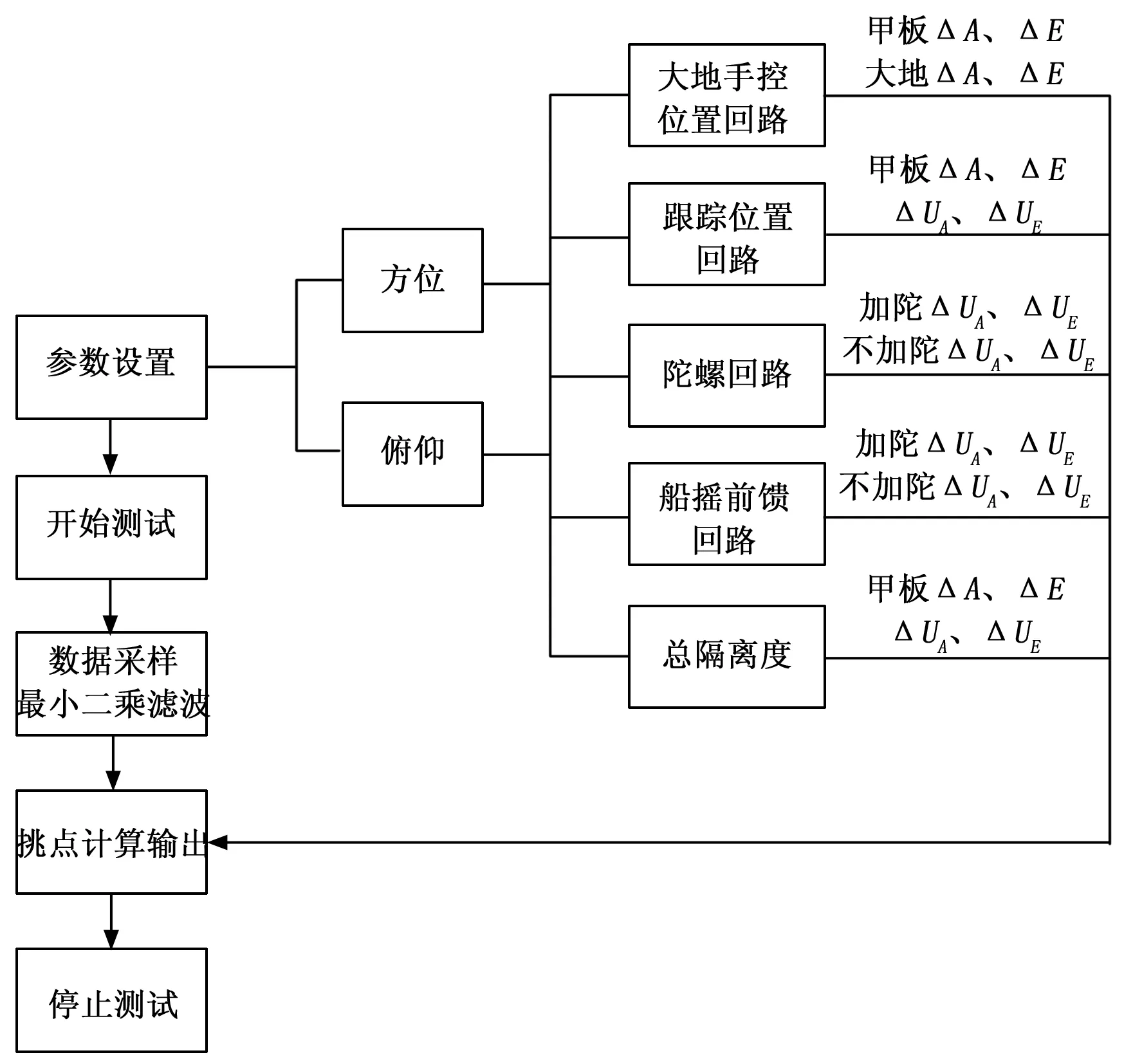
图6 船摇隔离度测试软件流程图
4 实验结果与分析
采用基于梯度型最小二乘滤波算法的船摇隔离度自动测试软件在船舶生摇的动态条件下进行船摇隔离度的计算,共进行了13组测试,并与人工挑点计算方法、加权滤波测试方法[14]作了对比,对比情况如附录所示。
扰动较小时以自跟踪状态(不加陀)的隔离度测试结果为例进行说明,如表2所示。
扰动较大时以跟踪位置回路(自跟踪+陀2+船馈)隔离度测试结果为例进行说明,如表3所示。

表2 自跟踪(不加陀)隔离度测试结果

表3 跟踪位置回路船摇隔离度测试结果
经比较分析,船摇扰动较小时(第1~7组数据),3种计算方法基本一致,最大偏差百分比在5%以内(偏差小于2 dB);船摇扰动较大时(第8~13组数据),加权滤波测试方法由于未能有效滤除扰动跳变量,引起隔离度计算结果明显偏大,偏差量大于9.5%(偏差大于4 dB),最大达到34%。而采用本文设计的基于梯度型最小二乘滤波算法的船摇隔离度自动测试方法与人工挑点计算结果仍一致(偏差量低于5%),验证了该方法的可靠性和有效性。研究表明,本文设计的测试方法能准确计算船摇隔离度,可替代人工挑点计算和现有软件测试方法。
5 结束语
本文分析了船摇隔离的基本原理,建立了梯度型最小二乘滤波模型,提出了对测量数据中的噪声分量进行滤波再通过VC++编程实现船摇隔离度的自动测试方法。借助船舶生摇的动态条件下利用基于梯度型最小二乘滤波算法的自动测试软件进行船摇隔离度计算,并与传统测试方法比对,验证了该处理方法的有效性,解决了传统测试方法效率低、误差大、操作复杂、且不能有效解决扰动跳变的不足,提高了伺服系统船摇隔离度的测试精度。由于实验技术条件的限制,该滤波算法仍存在滤波平滑度低的不足,在后续的船摇隔离度测试研究中,进一步开展针对性研究,为后续优化设计提供参考。采用梯度型最小二乘滤波算法的船摇隔离度自动测试软件快速完成船摇隔离度的测试,是一次大胆尝试与创新,更是对传统测试技术的有益革新。随着经验的不断积累以及相关难题的不断攻克,基于梯度型最小二乘滤波模型自动测试船摇隔离度的前景必将更加光明。
[1] 刘四方, 罗友明. 基于VC++的船摇隔离度自动化测试研究[J]. 控制系统,2008,24(2):36-53.
[2] 瞿元新, 周锦标, 谢 勇,等. 船载测控设备船摇隔离度自动化测试方法研究[J]. 飞行器测控学报, 2006, 25 (4): 62-65.
[3] 何 谦, 陶 敏, 丁求启,等. 卡尔曼滤波在船载雷达伺服速率陀螺中的应用[J]. 遥测遥控, 2012, 33 (1): 43-46.
[4] 李志坚, 周朝猛, 刘 咏,等. 隔离船摇补偿新方法[J]. 科学技术与工程, 2009, (19): 5736-5738.
[5] 何荣贤, 蒋 军. 大型船载卫通伺服随动系统船摇隔离度[J]. 陕西工学院学报,2005, 21 (2): 8-10.
[6] 鲁尽义. 速率陀螺应用方法研究[J]. 测控与通信, 114 (3): 1-10.
[7] 鲁新龙, 丁风海, 孙永江. 大型船载航天测控雷达船摇隔离度的分析[A]. 中国航空学会飞行力学学术交流会[C]. 2006.
[8] 陈小刚, 李志坚, 季 辉. 增加船载雷达位置环船摇隔离度方法研究[J]. 电子设计工程, 2015 (17): 105-107.
[9] 罗 浩, 赵厚奎, 杨津骁,等. 一种解决纯方位跟踪问题的新的最小二乘模型[J]. 火力与指挥控制, 2008, 33 (11): 137-143.
[10] 文如泉, 辛 锋, 肖永江. 最小二乘滤波算法在目标跟踪中的性能比较[J]. 萍乡高等专科学校学报, 2009, 26 (6): 20-23.
[11] 吴金美, 胡上成, 侯亚威,等. 基于最小二乘和最速梯度准则的船摇数据自适应滤波算法[J]. 海上测量与控制技术, 2016, 22 (1): 65-67.
[12] 罗 成, 陈利华. 最小二乘滤波算法在目标跟踪中的应用[J]. 湖北理工学院学报, 2010, 26 (3): 18-20.
[13] 马 林, 黄国雄, 凌贵军. 船载卫通天线跟踪陀螺零漂对捕获能力的影响分析[J]. 飞行器测控学报, 2010, 29 (6): 83-85.
[14] 刘桂英, 韩 莉, 邵联合. 可变加权因子的递推最小二乘辨识算法及应用[J]. 中国仪器仪表, 2006 (3): 59-61.
Research on Testing Method of Ship Shaking Isolation Based on Gradient Descent and Least-squares Filtering Algorithm
Cai Hao
(China Satellite Maritime Tracking & Control Department, Jiangyin 214431, China)
Traditional testing methods of ship shaking isolation need heavy workload, which has low efficiency and large error. Simultaneously the jitter caused by interference cannot be solved effectively. In order to solve these problems, the principle of ship shaking isolation is analyzed, and the model based on gradient descent and least-squares filtering algorithm is built, the filtering algorithm based on gradient descent and least squares is proposed to filter the measured data, the automated testing of ship shaking isolation is realized through VC++ programming, and the analysis of automated testing under the condition of ship shaking is carried out. Compared to the results tested by traditional methods, the simulation results show that the filtering algorithm which shortens testing time and improves the testing accuracy of ship shaking isolation could filter out random errors in the measurement data effectively, and the jitter caused by interference is significantly decreased.
gradient descent; least squares filtering; ship shaking isolation; automated testing
2016-12-10;
2017-02-06。
蔡 浩(1990-),男,山东泰安人,硕士研究生,主要从事航天测控(伺服控制)方向的研究。
1671-4598(2017)07-0021-04
10.16526/j.cnki.11-4762/tp.2017.07.005
TP3
A
