采用MFC压电作动器对复合材料悬臂板振动主动控制∗

李蒙 李凤明

（北京工业大学机电学院，北京 100124）

采用MFC压电作动器对复合材料悬臂板振动主动控制∗

李蒙 李凤明†

（北京工业大学机电学院，北京 100124）

针对复合材料层合悬臂板，在其上表面铺设压电纤维复合材料MFC作为作动器，同时在下表面对称铺设压电薄膜（PVDF）作为传感器，应用速度反馈控制方法研究其主动振动控制.运用Hamilton原理和假设模态法推导含多个MFC作动器的复合材料层合板的力电耦合结构运动方程，其中考虑了MFC作动器作为悬臂板附加质量及刚度的影响.基于模态控制力／力矩最大化的原则，将多对MFC作动器／PVDF传感器铺设在层合悬臂板前几个低阶模态应变最大的区域，通过算例得出结构受控前后的时域和频域响应以及各MFC作动器所需的控制电压曲线.讨论复合材料层合板纤维铺设角度不同情况下，作动器MFC铺设位置及压电纤维铺设方向的相应变化.

复合材料悬臂板， 压电纤维复合材料（MFC）， 纤维铺设角度， 模态控制

引言

随着航空航天飞行器、高速列车等运载装备速度的不断提高，以及纤维增强复合材料等轻质高强材料在机翼、机身与车身壁板等经常处于动载荷作用下的关键结构中的使用，工程结构振动及其控制问题日益突出，可能会由于振动产生疲劳甚至破坏.因而针对轻质复合材料层合板壳结构，研究其主动振动控制具有重要理论与实际应用价值.

在过去的二十多年里，国内外学者采用压电陶瓷PZT作为传感器和作动器，针对梁、板等结构的振动主动控制问题进行了广泛的研究，并且已相对较为成熟.然而，由于压电陶瓷PZT在实际应用中的局限性，比如容易出现脆性断裂以及很难粘贴在曲面结构上［1］，部分学者近些年已经逐渐采用具有优良韧性和驱动能力的压电纤维复合材料比如MFC等作为压电陶瓷PZT的潜在替代品来研究结构的振动主动控制问题.Heung Soo Kim［2］等将MFC作动器粘贴在圆柱壳的表面，通过理论与实验方法研究了其主动振动控制.Kovalovs A［3］等采用实验方法，将MFC作为作动器研究了悬臂梁和圆盘的振动主动控制.Giovanni Ferrari和 Marco Amabili［4］针对四边自由的泡沫夹芯板，采用分布式MFC作动器研究了其主动振动控制.范丽锋［5］基于MFC压电作动器，针对柔性梁研究了其主动振动控制问题.但总体上，相比于国外，国内学者采用MFC等压电纤维复合材料作为驱动器的振动主动控制研究还比较缺乏.

对于同样具有高可靠性并能够应用在曲面结构上的压电薄膜（PVDF），由于其压电常数远小于PZT和MFC，单片的PVDF不能提供足够的驱动力，因而 PVDF 通常被用作压电传感器［6，7］. 又由于PVDF的刚度系数远小于悬臂板和MFC［6］，本文建模过程中忽略了其作为传感器的附加质量及刚度的影响，但考虑了MFC作动器对主结构的刚度矩阵及质量矩阵的影响.

文中针对复合材料层合悬臂板，在文献［8-10］等的研究基础上，采用MFC作为作动器，PVDF作为传感器，应用Hamilton原理和假设模态法推导了含多个MFC作动器的复合材料层合板的力电耦合结构运动方程.然后基于模态控制力／力矩最大化的原则，对MFC作动器的位置进行了优化铺设，并得出了结构受控前后的时域和频域响应以及各作动器MFC上所需的控制电压.最后讨论了复合材料层合板纤维铺设角度不同情况下，MFC作动器铺设位置及压电纤维铺设方向的相应变化.

1 含MFC复合材料层合板的运动方程

1.1 MFC及其压电本构方程

压电纤维复合材料（MFC）是由美国航空航天局（NASA）的 Langley 研究中心研制［1］，由于其高应变驱动效率、定向驱动能力、高可靠性以及可粘贴于曲面结构等优良特性，MFC逐渐被广泛应用于结构形状及振动控制、压电能量采集和结构健康监测等领域［11］.MFC主要由压电纤维、电极、聚合物基体组成，包括MFC-d31和MFC-d33两种类型［11］.其中MFC-d31的极化方向沿厚度方向并垂直于压电纤维方向，而MFC-d33的极化方向沿压电纤维方向，其特殊的结构布局使得d33型的MFC能产生更大的驱动力［12］，本文所采用的MFC-d33结构简图及其电场分布如图 1［3］和图 2［13］所示.

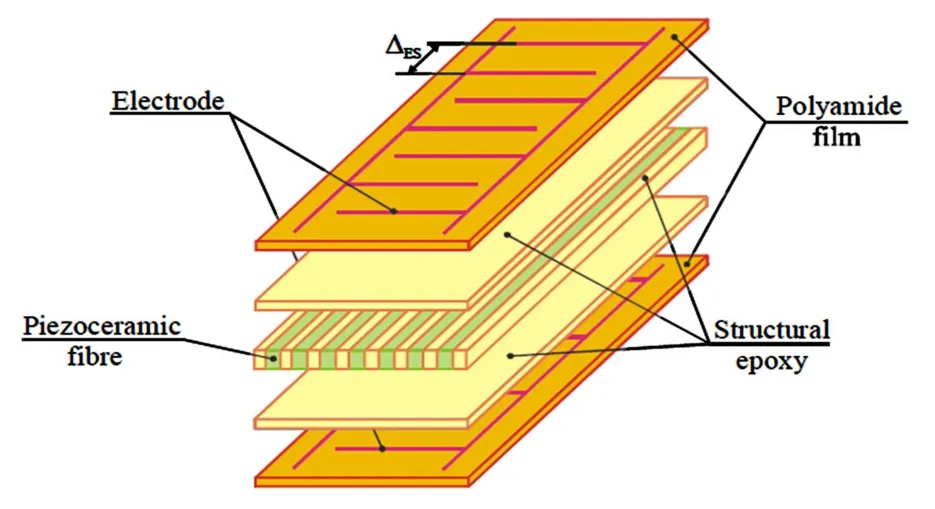
图1 MFC结构简图Fig.1 MFCconfiguration

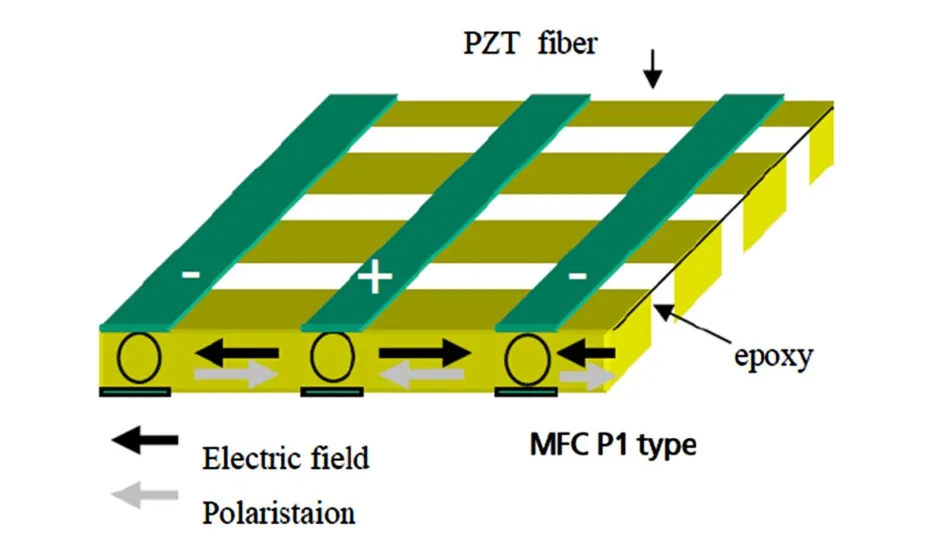
图2 MFC-d33电场分布Fig.2 Electrical field for MFC-d33

为简化MFC-d33较为复杂的电场分布，本文假设其电场在其电极之间是均匀分布的［14］，同时将MFC-d33看作是正交各向异性材料［12］，其压电方程为［12］:

式中{ σMFC}为MFC的应力向量，为MFC的正应力和切应力分量，为MFC的正应变和切应变分量，C11，C12，C22和 C66为 MFC 的刚度系数，E1（ ＝VMFC（t）／hE）和 D1分别为电场强度和电位移，VMFC（t）和hE分别为外加控制电压和电极之间的间距，e11，e12和∈11为压电应力常数和介电常数，［T］为与压电纤维角度有关的转换矩阵，具体请参见文献［12］．

同时，在文中作为压电传感器的PVDF，其压电效应类型及压电方程与传统的PZT类似，因而不再作详细介绍．

1.2 含MFC层合板力电耦合运动方程的建立

考虑图3所示含多对MFC的复合材料层合悬臂板结构，板的长、宽、厚度分别为a，b和h．设板的横向位移为w，以板的中面作为xOy平面，构建如图3所示的直角坐标系．

根据Kirchhoff薄板理论，悬臂板和MFC内任一点的面内和横向位移为:

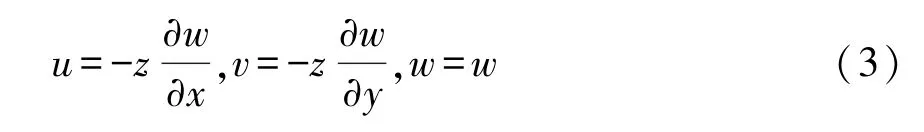
板和MFC的应变-位移关系如下:

式中｛ε｝代表板和 MFC 的应变向量，εx，εy，γxy代表板与MFC的正应变和切应变分量，［κ］为弯曲曲率向量．

图3 层合悬臂板结构Fig.3 Cantilevered laminated plate

板的本构方程为:

采用Hamilton原理和假设模态法建立结构的运动方程，Hamilton原理的具体表达式如下:

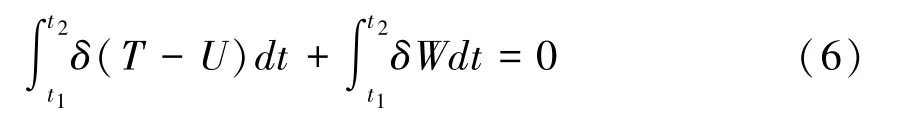
其中T，U和δW分别为含MFC悬臂板的总动能、总势能以及外力虚功．

结构的总动能T和总势能U表达式分别为:

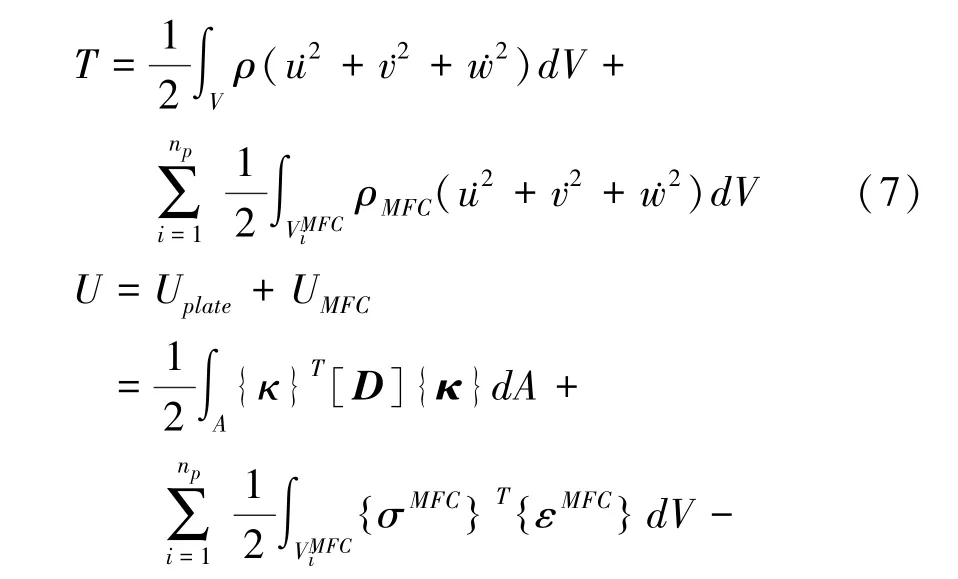
外力虚功δW表示为:

其中F（t）代表垂直于悬臂板的外激励，x0，y0是外激励作用点的横纵坐标．

应用假设模态法，将位移w表示为假设模态乘以广义坐标的形式:

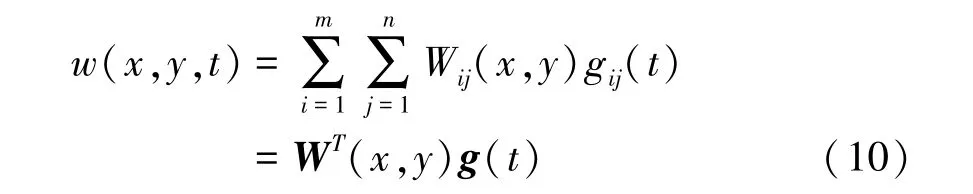
其中 g（t）为广义坐标；W（x，y）为满足结构几何边界条件的假设模态函数，m和n为模态阶数．g（t）和W（x，y）的具体表达式为:

由结构动力学可知，悬臂板模态函数Wmn（x，y）是沿x轴方向的悬臂梁型函数Xm（x）与沿y轴方向的自由梁型函数Yn（y）的乘积形式，即:

悬臂板模态函数中的Xm（x）和 Yn（y）稍复杂，具体形式请参见文献［8］．

将各式代入Hamilton原理表达式（6）以及假设模态法（10）～（12）的表达式，最终可以得到含MFC的复合材料层合悬臂板力电耦合运动方程:

式中M，K，MMFC和KMFC分别为层合板和MFC作动器的模态质量阵、模态刚度阵，为系统的力电耦合矩阵，它们均是关于模态函数Wmn（x，y）及其偏导数的表达式，VMFC为控制电压向量．

2 主动控制下的复合材料层合板运动方程

由第i个传感器PVDF变形产生的电荷量表示为:

其中Ai，Zi和分别为第i个PVDF的面积、中面纵坐标和电位移，e31，e32为PVDF的压电常数，，为PVDF的应变，其表达式与式（4）一致．

对上式应用假设模态法（10）～（12）的表达式可进一步得到:

式中∈33为PVDF的介电常数，hPVDF为PVDF的厚度．

将式（16）代入式（17）可得:

其中系数矩阵BiPVDF的表达式为:

由速度反馈控制算法得到作动器控制电压为:

式中Giv为第i对作动器／传感器的速度反馈增益．

将（18）和（20）代入（14）中，可得到主动控制下含有主动阻尼的复合材料悬臂板运动方程:

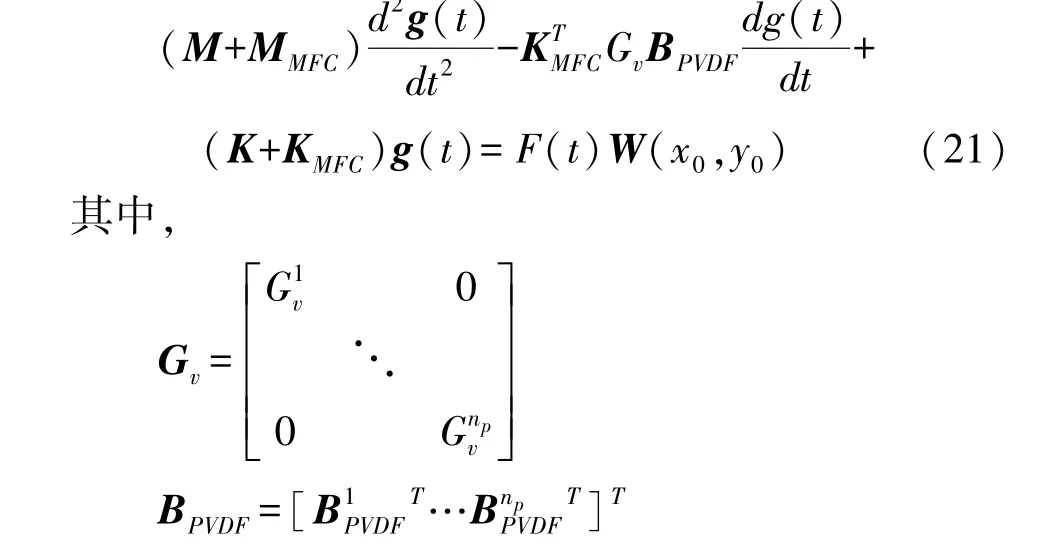
3 悬臂板振动主动控制分析

3.1 MFC作动器优化布置

为获得对受控结构的最大驱动力／力矩，压电作动器应当铺设在平均应变最大的区域，并且远离应变节线［15］.由结构动力学知识可知，振动产生的能量主要集中在低阶，因此算例中针对悬臂板的前三阶模态最大应变区域布置三对MFC作动器／PVDF传感器.最大应变区域可通过ANSYS模态分析得到，如图4所示.算例中的复合材料层合板长度为0.5m，宽度为0.25m，共10层对称铺设，铺设角为 [45°／-45°／45°／-45°／45°]s.

图4 悬臂板前三阶模态的应变分布Fig.4 Strain field of the first three modes

算例中，悬臂板的第一、二阶模态是弯曲模态，其对应 MFC作动器选取 d33型的 M8557-P1［16］（8557指的是85mm∗57mm），第三阶模态是扭转模态，对应 MFC作动器选取 d33型的 M8557-F1［16］（F1 指的是压电纤维铺设角度为 45°）. 得出的MFC作动器的位置铺设图如图5所示.

图5 MFC作动器铺设位置Fig.5 Location of MFC actuators

3.2 含MFC复合材料悬臂板的振动特性

以图5中MFC作动器铺设方案为例，计算含MFC的层合悬臂板固有频率.悬臂板及MFC作动器的材料常数如表1和2所示.

表1 复合材料悬臂板的材料常数Table 1 Materialparameters of the cantilevered plate

表2 MFC的材料及压电常数Table 2 Material andpiezoelectric parameters of MFC actuators

求解含MFC层合悬臂板运动方程（14）的特征方程，不考虑力电耦合项，可以获得含MFC压电作动器悬臂板的各阶固有频率，如表3所示.

表3 含MFC的复合材料悬臂板各阶固有频率Table 3 Natural frequencies of cantilevered laminated plate bonded with MFCs

同时计算了不考虑MFC影响的悬臂板各阶固有频率，其结果与有限元仿真结果良好吻合，从而可验证本文建模方法的正确性.同时，从表3可以看出，算例中压电作动器MFC质量及刚度的对悬臂板的固有特性的影响并不明显.

3.3 振动控制分析

应用速度反馈控制算法，对算例中层合悬臂板进行主动控制分析，其中MFC作动器／PVDF传感器的铺设位置仍如图5所示.

首先对悬臂板施加正弦激振力，通过求解方程（21）可得到受控前后结构在频域下的振动响应，如图6所示.

图6 受控前后悬臂板频域下振动响应Fig.6 Frequency responses of controlled and uncontrolled cantilevered plate

其中，三片MFC作动器单独作用下的控制效果如图7所示.可以看出，前三阶频率的振动响应在相应模态阶数MFC作动器的控制下，幅值显著减小.同时可看出第一、第三片MFC作动器也能降低第二阶频率下响应幅值.并且其他较高频率下的振动响应幅值也得到了抑制.

对于图7（a），由于第一片MFC作动器铺设在悬臂板固定端的中间位置，因此其对悬臂板弯曲模态即第一、二阶模态下的振动具有明显抑制效果，其对结构振动抑制的贡献最大，但同时可看出，第一片MFC作动器对于扭转模态即第三阶模态下的振动响应的控制效果并不明显.

图7（b）中，由于第二片MFC作动器铺设在远离悬臂板固定端的第二阶模态平均应变最大的区域，故可看出其对第二阶振动的抑制效果明显，而对于第一、三阶的影响相对较小.

由图7（c）可看出，第三阶模态即扭转模态对应的振动响应得到了显著控制，这是前两片MFC作动器所未能实现的.

图7 三片MFC作动器单独作用下的控制效果Fig.7 Controlperformance of single MFC actuator

总之，第一、二片MFC作动器对悬臂板弯曲振动的控制效果明显，而第三片MFC作动器对于悬臂板的扭转振动具有控制效果.

然后对悬臂板施加脉冲激励，可得到悬臂板受控前后结构在时域下的振动响应，如图8所示，其中包括第一、三片MFC作动器单独作用下的控制效果.

从图8中可看出，时域内与图7频域内振动控制结果相对应，三个MFC作动器同时作用时控制效果最为明显，同时可看出第一片MFC作动器对算例中悬臂板结构振动抑制的贡献最大.

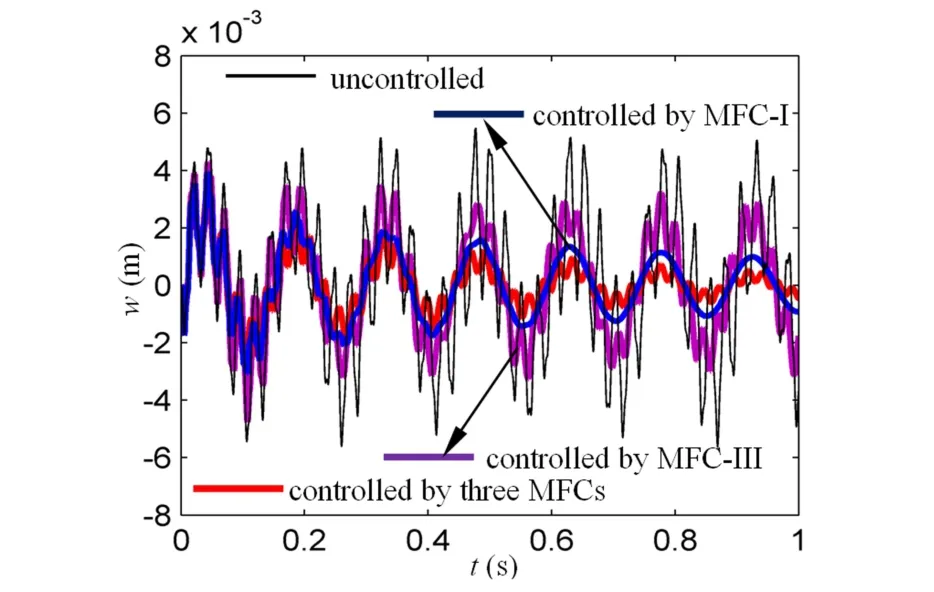
图8 悬臂板受控前后脉冲响应Fig.8 Time domain responses of controlled and uncontrolled cantilevered plate

同时，三片MFC作动器各自所需的控制电压如图9所示.可看出，其所需电压幅值均在MFC材料所允许范围之内.

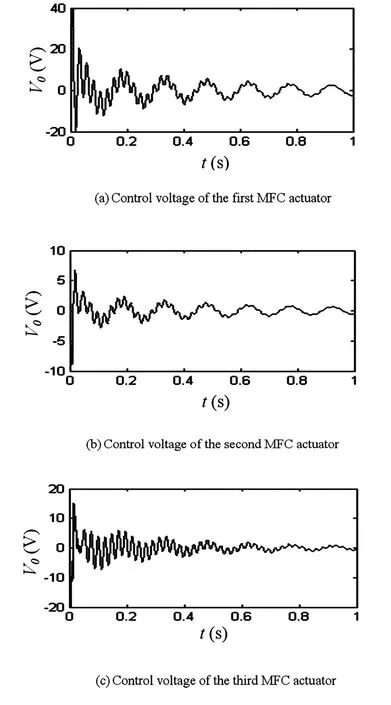
图9 三片MFC作动器所需控制电压Fig.9 Control voltages of the three MFC actuators

3.4 层合板纤维铺设角度的影响

考虑层合板纤维铺设角度的影响，针对不同纤维铺设角度的层合悬臂板，应用文中研究思路，即选取三片MFC作动器分别铺设在悬臂板前三阶的平均模态应变最大区域，分别得出其对应的MFC作动器的铺设位置，如图10所示.

图10 不同纤维铺设角度层合板的MFC作动器位置Fig.10 Placement of MFC actuators for cantilevered plate with different fiber orientation angle

图10中，压电纤维铺设角度为45°的MFC作动器仍然铺设在悬臂板扭转应变最大区域，从图中看出，不同纤维铺设角度对应的作动器铺设位置变动较大，而通过文中方法可有效获得其铺设位置.

4 结论

应用压电纤维复合材料MFC作为作动器，采用理论和数值分析方法，研究了不同铺设角度层合悬臂板的主动振动控制问题，得出了结构受控制前后的时域和频域响应，以及MFC作动器所需要的控制电压.

数值结果表明，采用压电复合材料MFC能有效地降低层合悬臂板结构的振动响应幅度，并且MFC作动器所需控制电压在工程允许范围之内.同时文中针对不同纤维铺设角度的层合悬臂板，首次给出了MFC作动器的具体铺设位置及方案，希望对实际工程中的层合板结构振动控制问题提供有价值的指导.

1 Williams R B，Grimsley B W，Inman D J，et al.Manufacturing and mechanics-based characterization of macro fiber composite actuators，In:ASME 2002 International Mechanical Engineering Congress And Exposition，2002:79～89

2 Kim H S，Sohn J W，Choi S B.Vibration control of a cylindrical shell structure using macro fiber composite actuators.Mechanics Based Design of Structures and Machines， 2011，39:491～506

3 Kovalovs A， Barkanov E， Gluhihs S.Active control of structures using macro-fiber composite （MFC）.Journal of Physics:Conference Series， 2007，93（1）

4 Ferrari G，Amabili M.Active vibration control of a sandwich plate by non-collocated positive position feedback.Journal of Sound and Vibration，2015，342:44～56

5 范丽锋.基于压电作动器MFC的柔性梁振动主动控制［硕士学位论文］.大连:大连理工大学，2014（Fan L F.Active vibration control of a flexible beam with piezoelectric MFC actuator［Master Thesis］.Dalian:Dalian University of Technology， 2014 （in Chinese） ）

6 Zhang Y H，Zhang X N，Xie S L.Adaptive vibration control of a cylindrical shell with laminated PVDF actuator.Acta Mechanica， 2010，210（1）:85～98

7 孟仁俊.PVDF压电薄膜传感器的研制［硕士学位论文］.上海:东华大学，2008（Meng R J.Fabrication of PVDF piezoelectric thin film sensor［Master Thesis］.Shanghai:Donghua University， 2008 （in Chinese））

8 Qiu Z C，Zhang X M，Wu H X，et al.Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate.Journal of Sound and Vibration， 2007，301:521～543

9 邱志成，吴宏鑫.基于特征模型的压电悬臂板振动控制.机械工程学报，2008，44（10）:187～195 （Qiu Z C，Wu H X.Vibration control for flexible smart cantilever plate based on characteristic model.Chinese Journal of Mechanical Engineering， 2008，44（10）:187～ 195 （in Chinese））

10 Eduardo P， Jun S O F， Eduardo A P， et al.Optimal placement of piezoelectric macrofiber composite patches on composite plates for vibration suppression.Latin American Journal of Solids and Structures， 2015，12:925～947

11 Lin X J， Zhou K C， Zhang X Y， et al.Development，modeling and application of piezoelectric fiber composites.Transactions of Nonferrous Metals Society of China， 2013，23（1）:98～107

12 Zhang S Q，Li Y X，Rüdiger S.Modeling and simulation of macro-fiber composite layered smart structures.Composite Structures， 2015，126:89～100

13 Andreas J S，Thomas D，Bent B，et al.Overview on Macro Fiber Composite Applications，Smart Structures and Materials:Active Materials:Behavior and Mechanics，2006，6170:61701k-8

14 Williams R B.Nonlinear mechanical and actuation characterization of piezoceramic fiber composites.Virginia Polytechnic Institute and State University，2004

15 Sharma V G M，Thakur N.Optimization criteria for optimal placement of piezoelectric sensors and actuators on a smart structure:A Technical Review.Journal of Intelligent Material Systems and Structures， 2010，21（12）:1227～1246

16 Smart Material Corp， ＜www.smart-material.com＞

ACTIVE VIBRATION CONTROL OF A CATILEVERED LAMINATED PLATE USING MFC ACTUATORS∗

Li Meng Li Fengming†
（College of Mechanical Engineering， Beijing University of Technology， Beijing 100124， China）

The active vibration control of a cantilevered laminated plate is investigated in this paper by using velocity feedback control method，where multiple macro fiber composite（MFC） and PVDF patches are bonded on the top and bottom surfaces of the plate to act as the actuators and sensors， respectively.By using Hamilton’s principle and the assumed mode method，the dynamical model of the structural systems is developed with considering the effects of mass and stiffness of MFC actuators.In order to obtain the maximum control forces or moments，the MFC actuators and PVDF sensors are placed in the regions with high average strain of host structure.Frequency and time domain responses of the cantilevered plate are obtained.And the required control voltages of MFC actuators are also calculated.Moreover，The placements of MFC actuators are presented for cantilevered laminated plate with different fiber orientation angle.

cantilevered laminated plate， MFC actuator， fiber orientation angle， modal control

4 March 2016，revised 11 April 2016.

10.6052／1672-6553-2017-003

2016-03-04收到第1稿，2016-04-11收到修改稿.

∗国家自然科学基金（11572007，11172084）

†通讯作者 E-mail:fmli＠bjut.edu.cn

∗The project supported by the National Natural Science Foundation of China（11572007，11172084）

† Corresponding author E-mail:fmli＠ bjut.edu.cn.