基于灰色理论模型对焦家金矿带新城矿区矿井涌水量预测研究
2017-08-28李天宇李维康
李天宇,李维康,王 敏
(山东科技大学地球科学与工程学院,山东 青岛 266590)
基于灰色理论模型对焦家金矿带新城矿区矿井涌水量预测研究
李天宇,李维康,王 敏
(山东科技大学地球科学与工程学院,山东 青岛 266590)
近年来,随着铁矿石和金矿石的开采,矿井涌水量预测越来越受到重视,而灰色理论,神经网络等新兴预测方法也越来越受欢迎。本文在大井法、比拟法的基础上,利用灰色理论建立GM(1,1)模型,对焦家金矿带新城矿区矿井涌水量进行了预测。对矿区2016年1~6月涌水量进行了计算和分析,矿井涌水量较稳定且较大,均在12 000 m3·min-1以上,稍有升高趋势,6月可达12 685.8 m3·min-1。最后将模型预测值与实际值比较,结果显示,精度达到96.481 67%,证明所建立模型较为可靠。为矿山进一步的建设和开采提供了技术资料。
新城矿区;涌水量预测;灰色理论;GM(1,1)模型
矿坑涌水历年来是矿山生产安全中的重大隐患,它妨碍施工进度、降低顶板稳固性、造成人员伤亡、财产损失等水害事故。因此预测涌水量大小显得尤为重要。矿井涌水量预测方法很多,如解析法,数值法,比拟法,回归/相关分析法,模糊数学模型,灰色系统理论,BP神经网络等等。解析法较简单但理想化,仅适用于水文地质相对简单的矿区;数值法必须借助计算机来进行,可解决复杂问题;比拟法简单但粗糙,要有基本条件相似的长期水量观测资料的老水井;回归分析法有效地避开了难以确定水文地质参数和机理的问题,但回归方程相关因子确定难度较大[1]。
以灰色理论为基础建立的模型所需资料较少,原理比较简单,计算方便,易于检验,预测精度较高,自从我国著名学者邓聚龙教授[2]20世纪70年代创立此理论以来,该理论已经在经济、气象、军事等众多领域得到了广泛应用。国内外很多学者对其进行了研究,灰色理论作为一门新兴理论,其应用领域和范围在不断丰富和发展。在矿井涌水量预测方面,邢爱国、胡厚田[3]在桑树坪矿1990—1997 年实测涌水量资料的基础上,应用灰色理论对该矿1998—2001 年的涌水量进行预测,解决了由于奥灰水水文地质条件不清,使11 煤迟迟不能开采的问题。肖有才、张秀成[4][5]等应用灰色理论分别对深埋型和浅埋型矿井的涌水量进行了预测;王苗[6]以灰色理论为基础,结合顶板涌水的各个影响因素对矿井顶板涌水量做出预测;钱家忠[7]、褚程程[8]也分别将其应用于矿井涌水量的预测,取得了较好的效果;李建林[9]建立GM(1,2)模型对王行庄煤矿矿井涌水量进行了预测;陈建宏[10]等人也以灰色理论为基础对某些矿区涌水量进行了预测。除了涌水量预测方面,冯民权[11]、彭涛[12]、武开福[13]等分别在水质、岩土和腾发量的研究中,通过构建等时距时间序列数据,关联度分析验证等取得了比较准确的预测结果;谷松[14]、王秀萍[15]、孙惠香[16]等对矿井瓦斯涌出量、边坡变形及地下结构爆炸冲击波峰值进行了预测,预测结果精度高,可用于指导工程实践。
由此看出,灰色系统理论应用较为成熟,而此方法目前还未被应用到焦家金矿带新城矿区的矿井涌水量预测中。前人用大井法和比拟法对焦家金矿带新城矿区涌水量进行了预测,大井法为理想化的模型,比拟法需有较全面的材料,而影响矿井涌水量的因素较多,其中很多具有不确定性,这两种方法适用范围均较局限,且预测的结果误差较大。本文根据多年涌水量数据,以灰色理论为核心,建立了GM(1,1)模型,并对其进行了检验,计算精度,然后对本矿区2016年6个月份涌水量进行了计算及分析,为矿山进一步的建设和开采提供了技术资料。
1 灰色理论模型公式的建立
设x(0)为原始数据系列,定义x(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)),则其累加序列(AGO序列)x(1)=(x(1)(1),x(1)(2),x(1)(3),…,x(1)(n)),AGO的计算方程式为:
x(0)(k)+x(1)(k-1)=x(1)(k)
(1)
灰模型GM(1,1)的定义型为:
x(0)(k)+az(1)(k)=b
(2)
式中:a为发展系数,反应系统的发展趋势;b为灰作用量,反映数据的变化关系;z(1)(k)序列称为白化背景值序列。
设z(1)=(z(1)(2),z(1)(3),z(1)(4),…,z(1)(n))
z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)
(3)
构造向量(a,b)称为GM(1,1)的一级参数包,C、D、E、F称为GM(1,1)的二级参数包。令:
(4)
(5)
(6)
(7)
将k=2,3,…,n分别代入式(2)中,将方程组转化为矩阵方程,再利用最小二乘法,可以得出:
(8)
(9)
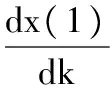
(10)
再利用累减运算对生成的数值进行还原:
(11)
灰色预测检验的方法一般有残差检验,关联度检验和后验差检验三种方法。本文用残差检验的方法进行检验,它是一种逐点检验的方法,通过各点的相对残差值,可以计算出预测模型的精度P。
设x1为实际值,x2为预测值,y为残差值,则残差:
y=x1-x2
(12)
相对残差:
(13)
平均残差:

(14)
精度:
P=1-e(0)(avg)
(15)

表1 2014-2015年新城矿区矿井涌水量实测值、累加序列及白化背景值序列
2 新城矿区基于灰色理论的涌水量计算
2.1 新城矿区矿井充水来源
焦家金矿带新城矿区位于莱州东北35 km处,属莱州市金城镇管辖,面积3.9 km2,区内地势平坦,地形起伏很小,属沿海平原。根据勘查报告可知,在隔水带未遭破坏的情况下,下部承压裂隙水是坑道充水的唯一直接来源,只有当隔水带破坏之后,上部无压裂隙水和第四系洪积-坡积层孔隙水才有可能进入坑道。渤海边处于影响半径之外,且未发现北西向导水构造,故对矿坑充水没有影响。本区年降水量不大但集中,且浅部裂隙发育,渗透条件较好,因此降水是影响坑道涌水量大小的重要因素。做好矿区的涌水量预测工作,对矿山正确设计及经济地开发资源十分重要。
2.2 涌水量计算模型
根据已知的2014-2015年新城矿区矿井实测涌水量,由公式(1)和(3)可得矿区2014-2015年涌水量的累加序列及白化背景值序列,见表1。依次代入式(4)(5)(6)(7)可得二级参数值:
C=3 028 303,D=251 572.9 ,E=34 132 584 754,F=5.200 15E+11。分别代入式(8)、(9)中,得:
a=-0.008 32,b=9 842.497
根据灰色理论模型可求得微分方程GM(1,1)的定义型:
x(0)(k)-0.008 32z(1)(k)=9 842.497
(16)
相应的白化响应式为:
(17)
对各点值进行预测,所得结果见表2。

表2 x(1)(k)的预测值及其精度检验
涌水量预测方法较多,前人对此地区进行过水文地质勘查,运用大井法计算所得精度约为80.23%,误差较大,比拟法误差也较大。由表2计算结果可知,以灰色理论为基础建立的GM(1,1)模型精度达96.481 67%,精度较高,可见此方法明显优于大井法和比拟法,适用于本矿区矿井的涌水量预测。
2.3 涌水量计算结果分析
将k=25,26,27,28,29,30分别代入白化响应式,对新城矿区2016年1月-6月涌水量进行计算,结果见表3。
由计算结果可知,新城矿区2016年1-6月矿井涌水量较稳定且较大,均在12 000 m3·min-1以上,稍有升高趋势,6月可达12 685.8m3·min-1,由降水量数据来看,莱州市2014年全年降水量为460.1 mm,2015年全年降水量为528.8 mm,2016年1月-6月月降水量较大且明显大于2014年和2015年相应月份的降水量,6月降水量达123.3 mm,1月降水量最小,为4.9 mm,除3月外,1月-6月降水量持续升高,因此推测2016年1月-6月的涌水量较大可能是由降水引起的,应引起重视,及时采取防水治水的措施,避免在金矿开采过程中大量水涌入危及矿山安全,引起人员伤亡。

表3 2016年1月-6月新城矿区矿井涌水量预测 m3·min-1
3 结语
焦家金矿带新城矿区是我国重要的金矿开采区,因此其矿井涌水量预测十分受重视。前人对此地区进行过水文地质勘查,运用大井法、比拟法计算误差较大。本文利用灰色理论建立了GM(1,1)模型,用已知数据进行了精度的检验,精度高达96.481 67%,证明方法合理,且这种方法计算方便,易于检验,明显优于大井法和比拟法。通过代入所得公式计算出了新城矿区2016年1月-6月涌水量,经分析,推测其涌水量较大可能是由这段时间该区的降水引起的,应引起重视,及时采取措施,避免矿区发生危险事故。
[1]左文喆,王斌海,程紫华,等. 矿井涌水量预测方法综述. IM&P 化工矿物与加工.2016.(9):71-74.
[2]邓聚龙. 灰色理论基础[M]. 武汉:华中科技大学出版社.1992.
[3]邢爱国,胡厚田. 灰色系统理论在矿井涌水量预测研究中的应用[J]. 中国矿业.1999.8(6):75-77.
[4]肖有才,张秀成,王宏艳. 灰色理论在预测深埋型矿井涌水量中的应用[J]. 辽宁工程技术大学学报.2004.23(2):175-177.
[5]肖有才,张秀成,顾志明. 浅埋型矿井涌水量预测预报的灰色模型[J]. 中国安全科学学报.2004.14(5):18-20.
[6]王苗. 基于灰色理论的矿井顶板涌水量预测模型的建立与应用[D]. 青岛:山东科技大学.2008.
[7]钱家忠,朱学愚,吴剑锋,等. 矿井涌水量的灰色马尔科夫预报模型[J]. 煤炭学报.2000.25(1):71-75.
[8]褚程程,杨滨滨. 灰色理论在矿井涌水量预测中的应用[J]. 煤田地质与勘探.2012.40(2):55-58.
[9]李建林,李志强,郑继东,等. 矿井涌水量灰色GM( 1,2) 预测模型[J]. 河南理工大学学报( 自然科学版).2016.35( 3) : 368-372.
[10]陈建宏,施飞,郑海力,等. 基于灰色神经网络的矿井涌水量预测. 矿业研究与开发.2011.31(2):73-75.
[11]冯民权,邢肖鹏,薛鹏松. BP 网络马尔可夫模型的水质预测研究—基于灰色关联分析[J]. 自然灾害学报.2011.20(5):169-175.
[12]彭涛,杨岸英,梁杏,等. BP 神经网络-灰色系统联合模型预测软基沉降量[J]. 岩土力学.2005.26(11):1810-1814.
[13]武开福. 基于灰色关联度与BP 神经网络模型的日参考作物腾发量预测[J]. 水土保持研究.2011.18(2):237-240.
[14]谷松,崔洪庆,冯文丽. 基于灰色理论的小波神经网络对瓦斯涌出量的预测[J]. 煤炭学报.2007.32(9):964-966.
[15]王秀萍,吴清海,赵宝锋. 灰色模型联合小波变换进行变形预测的研究[J]. 工程勘察.2006(12):66-68.
[16]孙惠香,许金余,范珉. 地下结构中爆炸冲击波峰值压力衰减规律灰色小波预测[J]. 煤炭学报.2011.36(增刊2):406-410.
[17]桂祥友,郁钟铭,孟絮屹. 贵州煤矿瓦斯涌出量灰色预测的应用[J]. 采矿与安全工程学报.2007.24(4):450-452.
[18]张耀峰. 动态灰色理论模型在路基沉降预测中的应用[J]. 公路.2010.4(4):45-47.
[19]雷学文,白世伟,孟庆山. 灰色预测在软土地基沉降分析中的应用[J]. 岩土力学.2000.21(2):145-147.
[20]彭苏萍,孟召平. 矿井工程地质理论与实践[M]. 北京:地质出版社.2002.
[21]刘思峰. 灰色系统理论的产生与发展[J]. 南京航空航天大学学报.2004.36(2):267-272.
[22]李孜军. 1992—2001 年我国灰色系统理论应用研究进展[J]. 系统工程.2003.21(5):8-12.
[23]亓协全, 李爽,董妍. 辽宁省北票市台吉营子矿区金矿水文地质条件及矿坑涌水量预测. 化工矿产地质.2016.38(1):53-59.
[24]刘娟,杨国勇,孟茜. 新驿煤矿矿井涌水量预测. 山东煤炭科技.2008.(1):74-76.
[25]温文富,曹丽文. 比拟法和解析法在某矿井涌水量预测中的分析比较.中国煤炭.2011.37(7):38-40.
[26]朱愿福,王长申,李彦周,等. 改进的灰色系统理论预测矿井涌水量. 煤田地质与勘探.2014.42(4):44-50.
[27]肖云,田昌贵,李元松. 基于GM(1,1)模型的铜绿山矿井水害预测与防治. 安全与环境工程.2013.20(1):115-119.
[28]KAYACAN E,ULATAS B,KAYNAK O. Grey system theory-based models in time series prediction[J]. Expert Systemswith Applications,2010.37(2):1784-1789.
[29]Wang Qingyin ,Wu Heqing. The concept of grey number and its property. In : Proceedings of NAFIPS’98.USA ,1998.45-49.
Predicted Study on Mine Water Inflow in Xincheng Mining Area of Jiaojia Gold Mine Based on Gray Theory Model
LI Tian-yu, LI Wei-kang, WANG Min
(School of Earth Science and Engineering, Shandong University of Science and Technology, Shandong Qingdao,266590)
In recent years, with the exploitation of iron ore and gold ore, the prediction of mine water inflow has been paid more and more attention, and gray prediction theory, neural network and other emerging forecast methods are getting more and more popular. Based on the large well method and the comparison method, the GM (1,1) model is established by using the gray theory, and the water inflow of the Xincheng mining area in the Jiaojia gold belt is predicted. The water inflow from January to June, 2016 of the mining area is calculated and analyzed. The mine water inflow is stable and large, all of which are above 12000, and the trend is slightly higher, which is reaching to 12685.8 in June. Finally, the model predicted values are compared with the actual values, it shows that the accuracy is 96.481 67%, which proves that the model is reliable. This study provides technical information for the further construction and mining of the mine.
Xincheng Mining Area; prediction of mine water inflow; Gray Theory; the GM (1,1) model
2017-05-05
校研究生教育创新计划项目(KDYC150006);山东省地质勘查优选项目:“胶西北金矿集中区矿坑充水机理及矿坑水综合利用研究”(鲁勘字(2015)25号)
李天宇(1995-),女,山东济南人,主攻方向:水文与水资源。
P641.4+1
A
1004-1184(2017)04-0009-04
