含水率对混凝土弹性简支梁受力特性影响分析
2017-08-28朱俊阁李宗利
朱俊阁,李宗利
(西北农林科技大学水利与建筑工程学院,陕西杨凌712100)
含水率对混凝土弹性简支梁受力特性影响分析
朱俊阁,李宗利
(西北农林科技大学水利与建筑工程学院,陕西杨凌712100)
含水率对混凝土力学性能有较大的影响,目前对混凝土含水率的研究主要集中在对混凝土材料的物理试验上,对混凝土构件的理论研究鲜有报道。假定混凝土梁中含水率沿截面高度的变化规律,得到均布荷载作用下梁中应力及挠度的显示表达式,并结合算例给出不同含水率分布情况下混凝土简支梁典型断面应力及挠度分布规律,探讨含水率变化对梁受力特性的影响规律,为服役在水位变幅工况下的混凝土结构的安全度评价提供理论依据。
含水率分布;应力;挠度;理论分析
在水环境中工作的混凝土结构,如大坝、海岸及近海岸的结构物、渡槽、桥墩以及服役在浪溅区和水位变动区的海工建筑物,受到水位变幅的影响,导致结构物中含水率呈现周期性变化,如结构物会从饱和状态经过自然干燥达到干燥状态,又可由干燥状态经过毛细吸水、水分扩散和压力渗透逐渐达到饱和,期间结构物中含水率分布不均匀,横截面会形成含水率分布梯度。由于混凝土的力学性能受其含水率影响,导致混凝土构件变形性能的变化,从而影响其变形和安全度的合理评价。
关于含水率对混凝土材料性能的研究,已经取得了较多的成果,且这些成果基本上已经成为共识[1-7]。在混凝土材料及试验条件都相同的情况下,混凝土的静力强度随着混凝土含水率的增加而降低,但弹性模量却在提高。Cadoni等[1],Liu等[5],Yaman、Hearn等[6-7]都通过试验研究得到相同的结论。但他们的研究基本是对混凝土材料开展的试验研究,关于水对于混凝土构件的研究则较少。杨骁等[8]建立了饱和多孔弹性Timoshenko梁大挠度弯曲变形的非线性数学模型;李丽,杨骁[9]研究了微观不可压饱和多孔弹性梁大挠度拟静态响应的一维非线性数学模型,给出了梁弯曲时挠度及弯矩随时间的响应曲线。这些研究都是建立在饱和梁基础之上,即梁为均质的,而当梁内水分布不均时,混凝土弹性模量受水分的影响,其均质性受到破坏,此时再按均质梁理论研究梁的受力特性是否合理是本文要探讨的问题。
本文基于Liu等[5]的研究成果,认为混凝土含水率与其弹性模量存在明确的函数关系,以实际工作中水平放置的梁为例,假设含水率沿梁的截面高度变化,将不同含水率分布条件下的混凝土简支梁看作功能梯度梁,在弹性力学[10]基础上应用应力函数半逆解法推求在均布荷载作用下梁中应力挠度显示表达式[11-15],间接得到应力及挠度与含水率之间的函数关系,分析不同含水率分布对混凝土简支梁性能的影响规律。
1 实例分析
矩形截面混凝土简支梁受均布荷载q的作用,跨度为2l,高度为h,荷载分布如图1所示。

图1 模型尺寸
由于泊松比受含水率变化的影响不大[16],所以本文取一恒定值为μ。由文献[17]可知混凝土含水率范围一般在0~5%,为此假定混凝土简支梁中含水率分布函数为
ω=5×(0.5+z/h)n
(1)
式中,z为坐标纵轴,mm;ω为含水率,%;h为简支梁高,mm;n为表示梁中不同含水率分布规律的参数,当n=0时,表示混凝土梁处于饱和状态,此时梁的含水率为5%;当n=1,2,3时表示梁中含水率沿高度的分布规律,n越大梁中含水率分布越不均匀。
文献[5]研究表明,混凝土弹性模量受含水率的变化而变化,定义了C30混凝土弹性模量与含水率之间的关系式为
E=1 982.3ω+25 802
(2)
式中,E为弹性模量,MPa;ω为混凝土的含水率,%,当ω=0时,梁处于干燥状态;当ω=5时,梁处于饱和状态。
将式(1)代入式(2)可得
E(z)=9 911.5×(0.5+z/h)n+25 802
(3)
利用应力函数半逆解法[15],可设应力函数

(4)
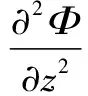
(5)
将式(5)代入平面应力状态本构方程中有
(6)
其对任意x均成立,故而可得
(7)
解方程(7)第一式可得
(8)
解方程(7)第二式可得

(9)
将以上结果代入几何方程中可得
(10)


(11)
要使式(11)成立,方程左右两边都为常数a。此时可得
(12)
式中,a,u0,w0为常数。
综上所述给出应力、应变与位移的解析显示表达式
(13)
(14)
式中,C1、C2、C3、C4、C5、C6、u0、w0均为常数,常数用边界条件确定。
通过对式(3)中n赋予不同的值,利用公式(13)、(14)可得到不同含水率分布下该弹性简支梁典型断面的应力和挠度的分布规律,通过对比分析,得到不同含水率分布对梁力学特性的影响规律。
2 结果分析
本文分别令n=1,2,3,表达梁中不同含水率分布,如图2所示。在此含水率分布情况下,针对图1所示算例,取q=1 000 kPa,l=1 m,b=150 mm,h=120 mm,μ=0.2,可得混凝土简支梁典型断面的应力和挠度的分布规律,结果如图3~5所示。

图2 梁含水率分布规律

图3 跨中截面应力分布规律

图4 支座截面剪应力分布规律

图5 梁挠度分布规律
从图3a看以看出,当梁处于干燥和饱和状态时,梁为不同含水率的均质梁,梁应力为直线分布,符合一般均质梁的应力分布规律;当含水率遵循幂率分布时(即n=1,2,3),其应力为曲线分布,且随着n的增大,梁中含水率分布越不均匀,中性轴分别往下偏离了0.028、0.025、0.03 mm。最大拉应力和最大压应力分别出现在截面的底部和顶部,且n=1,2,3时最大拉应力比梁处于干燥或饱和状态时分别增大了10.87%、14.32%和16.69%,而最大压应力却分别减小了10.87%、7.58%和6.43%。试验结果表明[1,[3],混凝土的抗拉强度随含水率的增大而减小,但在该情况下其最大拉应力却随着含水率的分布不均而增大,若以梁均质状态下的最大水平拉应力作为梁是否破坏的判断依据对其进行安全度评价显然是不合理的。
从图3b可以看出,含水率分布基本上不影响其竖向应力分布。
从图4可以看出,当梁处于干燥或饱和状态时,τxz关于几何中面对称;而当n=1,2,3时,τxz不再关于几何中面对称,最大剪应力的位置往下部偏移,且当n=1时,最大剪应力增大了0.2%,当n=2,3时,最大剪应力分别减小了0.84%和1.1%。
从图5可以看出,梁处于干燥状态时挠度最大,与之相比,随着n的增大,最大挠度分别减小了27.8%、15.4%、12.5%和11.1%,此时若以梁在干燥状态下的最大挠度对其进行安全度评价是过于保守的。
3 结 语
(1)混凝土的弹性模量因含水率不同而变化,其均质性受到破坏,仍按均质梁进行应力、挠度计算明显不合理。
(2)当梁中含水率沿截面高度变化时,对截面水平正应力影响较大,其最大拉应力比梁处于干燥或饱和状态时大,但对竖向应力和剪应力则影响较小。此时若以梁在均质状态下的最大水平拉应力作为梁是否破坏的判断依据,则高估其承载力。
(3)对于不同含水率的梁,因弹性模量随含水率的增大而变大,则梁的刚度提高,其挠度减小,按均质梁理论计算其挠度则过于保守,应根据梁服役的工况合理选择其挠度计算方法。
[1]CADONI E, LABIBES K, ALBEITINI C, et al. Strain-rate effect on the tensile behavior of concrete at different relative humidity levels[J]. Materials and Structures, 2001, 34(1): 21- 26.
[2]闫东明, 林皋. 不同初始静态荷载下混凝土动态抗压特性试验研究[J]. 水利学报, 2006, 37(3): 360- 364.
[3]王海龙, 李庆斌. 不同加载速率下饱和混凝土的劈拉试验研究及强度变化机理[J]. 工程力学, 2007, 24(2): 105- 109.
[4]张国辉, 李宗利, 聂抗议, 等. 不同含水率混凝土断裂韧度试验研究[J]. 水力发电学报, 2016, 35(2):1- 8.
[5]LIU B D, LÜ W J, LI L, et al. Effect of moisture content on static compressive elasticity modulus of concrete[J]. Construction and Building Materials, 2014, 69: 133- 142.
[6]YAMAN I O, HEAM N, AKTAN H M. Active and non-active porosity in concrete, part I: Experimental evidence[J]. Materials and Structures, 2002, 35(3): 102- 109.
[7]YAMAN I O, HEAM N, AKTAN H M. Active and non-active porosity in concrete, part II: Evaluation of existing models[J]. Materials and Structures, 2002, 35(3): 110- 116.[8]杨骁, 吕新华. 饱和多孔弹性Timoshenko梁的大挠度分析[J]. 固体力学学报, 2012, 33(1): 103- 110.
[9]李丽, 杨骁. 简支饱和多孔弹性梁的非线性弯曲[J]. 力学季刊, 2007, 28(1): 86- 91.
[10]徐芝纶. 弹性力学简明教程[M]. 第3版. 北京: 高等教育出版社, 2002.
[11]SANKAR B V. An elasticity solution for functionally graded beams[J]. Composites Science and Technology, 2001(61): 689- 696.
[12]仲政, 于涛. 功能梯度悬臂梁弯曲问题的解析解[J]. 同济大学学报: 自然科学版, 2006, 27(1): 443- 447.
[13]于涛, 仲政. 均布荷载作用下功能梯度悬臂梁弯曲问题的解析解[J]. 固体力学学报, 2006, 27(1): 15- 20.
[14]黄德进, 丁皓江, 陈伟球. 任意荷载作用下各向异性功能梯度梁的解析解和半解析解[J]. 中国科学G辑: 物理学 力学 天文学, 2009, 39(6): 830- 842.
[15]李东华, 朱锡, 梅志远, 等. 均布荷载作用下功能梯度简支梁弯曲的解析解[J]. 力学与实践, 2012, 34(1): 39- 47.
[16]CHI Shyangho, CHUNG Yenling. Mechanical behavior of functionally graded material plates under transverse load-part I: Analysis[J]. International Journal of Solids and Structures, 2006(43): 3657- 3674.
[17]刘保东, 李鹏飞, 李林, 等. 混凝土含水率对强度影响的试验[J]. 北京交通大学学报, 2011, 35(1): 9- 12.
(责任编辑焦雪梅)
EffectofMoistureContentonElasticConcreteSimplySupportedBeam
ZHU Junge, LI Zongli
(College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, Shaanxi, China)
The mechanical properties of concrete are significantly affected by moisture content. At present, the researches on moisture content of concrete mostly focuses on physical test of concrete materials, but the theoretical analysis on concrete structures is rarely reported. After assuming the distribution law of moisture content along the height of cross section in simply supported beam, the explicit analytical expressions of stress and deflection of concrete beam subjected to uniform pressure can be obtained, and the stress and deflection of typical cross section under different moisture content distribution can be got for a case. The influences of different moisture content distribution on the mechanical properties of concrete beam are discussed, which provides a theoretical basis for the safety evaluation of concrete structures serving under water level fluctuation condition.
distribution of moisture content; stress; deflection; theoretical analysis
2017- 01- 05
国家自然科学基金面上项目(51379178);中央高校基本科研业务费专项资助项目(ZD2012015)
朱俊阁(1989—),男,河南郑州人,硕士研究生,研究方向水工结构设计;李宗利(通讯作者).
TU313.1
:A
:0559- 9342(2017)06- 0043- 04
