平台单星复合制导方法研究
2017-08-28常晓华
张 婕, 王 智, 常晓华, 洪 蓓
(北京宇航系统工程研究所,北京 100076)
平台单星复合制导方法研究
张 婕, 王 智, 常晓华, 洪 蓓
(北京宇航系统工程研究所,北京 100076)
为了提高武器命中精度,开展了平台单星复合制导方法研究。通过建立星敏感器观测量、平台失调角与落点偏差之间的联系,构建星光修正模型;同时利用数值寻优方法确定最佳星方位。仿真证实,平台单星制导方法能够有效降低制导工具误差,是提高导弹命中精度的有效手段。
制导; 最佳星; 命中精度
0 引言
星光制导是在纯惯性制导的基础上辅以星光修正,利用恒星在空间的方位基准来校准平台坐标系与发射惯性系之间的误差角。因此凡是引起惯性基准方位漂移(能够测量到的)的误差,都可以通过星光制导进行修正[1]。
星光制导是一种全自主式制导方式,战时无需依赖任何外界保障,具有不被干扰的优点,同时对提高纯惯性制导武器的命中精度大有益处,因而各国导弹武器加强了对星光制导的使用[2]。苏联SS-N-8是最早采用星光制导的潜地远程弹道导弹,SS-N-18、SS-N-20也应用了星光制导。美国考虑到导弹空间尺寸较小,对单星方案进行了大量的研究,三叉戟I、三叉戟II都是采用测单星方案,而且精度很高[3]。我国从20世纪80年代起开展这项技术的研究,并取得一定的成果。早期由于工业水平的制约,限制了星敏感器在平台上的安装,提出将星敏感器捷联安装在平台基座上的方案,由于平台框架角传感器的测量精度低,导致制导精度不高。随着工业水平的提高,星敏感器安装在平台台体上得以实现。
本文针对星光+平台的单星复合制导方案,对星光制导模型进行推导,寻求最佳星方位确定方法,并通过仿真检验星光修正的效果,以期为提高导弹命中精度提供有效的技术手段。
1 星光制导原理
1.1 概述
由于平台的体积有限制不可能安装两个星敏感器,同时平台是惯性的基准不允许飞行中作任意旋转,因此安装在平台上的星敏感器只能测量一颗星,称单星方案[4]。测量一颗星只能得到两个参数,而要确定绕平台3个轴的3个角度变化是有困难的,但最后修正的落点偏差只有两个参数,因此在选择合适的恒星作导航星后也能达到目的(见图1)。

图1 星敏感器示意图Fig.1 Schematic figure of star sensor
1.2 修正原理
1.2.1 角度定义
星体在发射惯性系内的方位如图2所示,分别用高低角e和方位角σ表示方位角,极性符合右手定则[5]。考虑光路传递与平台结构安装的关系,将星敏感器以一定的角度安装在平台上,分别用φ0、ψ0表示安装角,极性符合右手定则,示意图见图3。
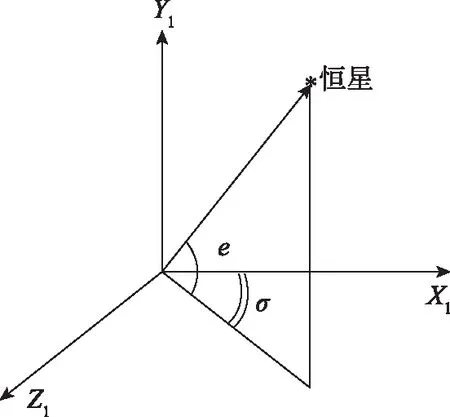
图2 星体在发射惯性系内的投影示意图Fig.2 Schematic figure of the projection of the star in the launch inertial frame
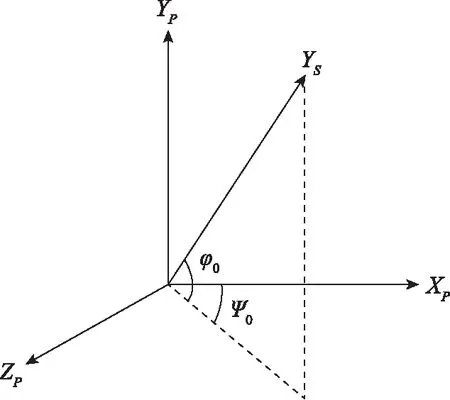
图3 星敏感器安装角度φ0、ψ0示意图Fig.3 Schematic figure of star sensor installation angle φ0、ψ0
失调角为平台坐标系3个坐标轴相对理论平台惯性坐标系的转动角度,定义沿平台三轴的失调角为αx、αy、αz。
1.2.2 修正模型
根据图2,星体在发射惯性坐标系内可以表示为:
S=cosσ·cose·i+sine·j-sinσ·cose·k
(1)
根据坐标系转化关系可以得到式(2):
(2)
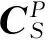
星体向量在星敏感器坐标系内的表达式为:
S=ΔφS·iS+jS+ΔψS·kS
(3)
其中ΔφS、ΔψS是星敏感器测量量。
将两式进行联立,可以得到2个测量量与3个失调角之间的关系式。
(4)
其中,
记式(4):
CC1·α=V3
(5)
其中α是平台失调角。
(6)
其中ul,s、uh,s为最佳估计系数:
(7)
据各惯性器件的误差模型,可以得到平台失调角的表达式:
(8)
其中,K为误差系数,C2是平台失调角对误差系数的偏导数矩阵。
考虑平台各误差,则工具误差引起的视加速度误差为:
(9)

(10)
(11)
定义矩阵:
(12)
(13)
(14)
记:
(15)
其中,PL是落点纵向偏差对关机点速度、位置偏导数矩阵,PH是落点横向偏差对关机点速度、位置偏导数矩阵。
则工具误差引起的落点偏差为:
(16)
根据式(6)和式(16),星光修正后的落点偏差为:
(17)
1.2.3 最佳估计系数
从上面的推导可以看出,利用落点偏差表达式可以计算得到导弹落点偏差CEP[6]。利用落点偏差CEP对最佳估计系数求导,并令导数为0即可计算最佳系数表达式uls、uhs。
(18)
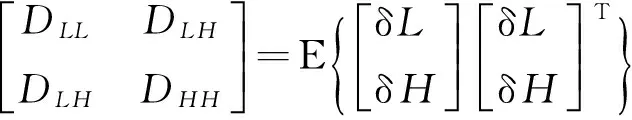
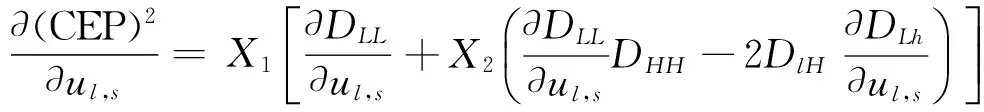
(19)
(20)
其中,
2 最佳星方位确定
单星方案修正后的精度与所选导航星的方位e、σ有关,选不同方位的星作导航星,对落点的修正效果不同,因此要寻找最佳或接近于最佳星的方位。寻找最佳星方位有两种方法:一种是求极值,另一种是数值寻优。
2.1 求极值方法确定最佳星方位
为计算出最佳星的方位,令:
(21)
求出最佳星的方位(e*,σ*)。但是这种方法要解超越方程组,不利于工程实现。
2.2 数值寻优确定最佳星方位
为了研究星光修正效果随星体方位的变化规律,令高低角、方位角在e∈(0°~180°),σ∈(0°~360°)范围内变化,循环计算星光修正后的工具误差造成的落点CEP,其中最小CEP对应的星光方位为最佳星方位。
3 星光修正效果仿真分析
基于10000km大射程弹道,采用数值寻优方法进行最佳星方位寻优,计算结果见图4。

图4 不同星体方位对落点精度的影响Fig.4 The influence of different star azimuth on the accuracy of the drop point
通过数据分析e=25°,σ=0°的方位是最佳星方位。用e=25°平面截图4,得到图5。用σ=0°平面截图4,得到图6。从图5、图6可知星光修正后的精度,随e或σ的变化呈周期性规律。
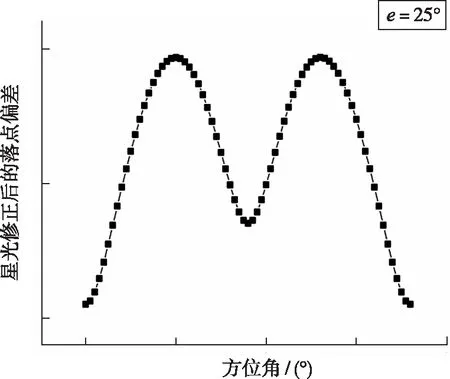
图5 e=25°截图Fig.5 The correction residual errors of drop point vary with azimuth angle when e=25°
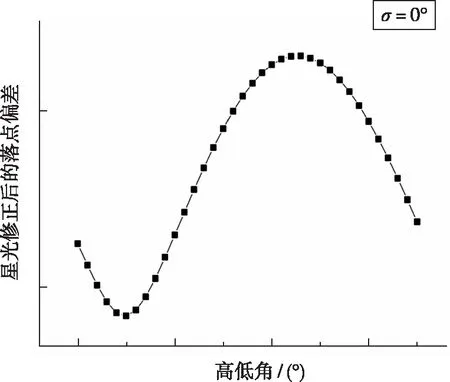
图6 σ=0°截图Fig.6 The correction residual errors of drop point vary with altitude angle when σ=0°
仿真计算表明,平台星光复合制导对平台误差系数中引起基准变化的项具有显著的修正效果,修正后平台误差系数引起的落点偏差降低了60%~70%,导弹系统命中总精度提高65%以上。
[1] 王永刚,刘新学.地地导弹制导原理与方法[M].西安:第二炮兵工程学院出版社,2002.
[2] 房建成,宁晓琳.航天器自主导航原理与方法[M].北京:国防工业出版社,2006.
[3] 张宗美.星光惯性制导系统[J].导弹与航天运载技术,1985(2):13-27.
[4] 肖称贵.单星-星光制导方案[J].航天控制,1997,15(1):11-16.
[5] 张谦.星光-惯性复合制导系统[J].导弹与航天运载技术,1993(3):37-42.
[6] Rounds S F. Stellar-inertial guidance capability for advanced ICBM[R]. AIAA 1983-2297,1983.
[7] 周海.星光/惯性组合制导系统设计[J].战术导弹控制技术,2006(3):37-40.
[8] 杨波,柴艳,秦永元. 基于惯性/星敏感器的高精度定姿方法研究[J].航空兵器,2007(3):15-19.
[9] 肖称贵.捷联星光制导方案与误差研究[J].导弹与航天运载技术,1997(4):1-8.
[10] 叶兵.星光/惯性复合制导最佳星快速确定方法与精度分析[D].长沙:国防科学技术大学,2008.
[11] 金振山,申功勋.适合于机动弹道导弹的星光-惯性组合制导系统研究[D].航空学报,2005,26(2):168-172.
[12] Fan Z.Current state of the development of star light inertial guidance technology and performance analysis[R].ADA310487,1996,5.
Research on Inertial/Celestial Integrated Guidance System of Single Star
ZHANG Jie, WANG Zhi, CHANG Xiao-hua, Hong Bei
(Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)
In order to improve hit accuracy, inertial/celestial integrated guidance system of single star is researched. Through the establishment of the connection between the star sensor observables, platform disorders angle and impact point deviation, the celestial navigation correction model is built. Through numerical method on the orientation of the optimal single star is determined. Mathematical simulating results show that celestial navigation of single star can reduce guidance instrument error.It is an effective means to improve the hit accuracy.
Guidance; Optimal star; Hit accuracy
2017-02-27;
2017-04-25
张婕(1972-),女,硕士,研究员,主要从事制导与精度分析方面研究。E-mail:zcnn0314@qq.com
V412.2
A
2096-4080(2017)02-0007-05
