几类冠图的Zagreb指数

王狄建，肖香凤，汤自凯

(湖南师范大学 数学与计算机科学学院，湖南 长沙，410081)

几类冠图的Zagreb指数

王狄建，肖香凤，汤自凯

(湖南师范大学 数学与计算机科学学院，湖南 长沙，410081)

设G=(V,E)是一个简单连通图，V和E分别为G的顶点集和边集。图的Zagreb指数是化学图论中一种重要的拓扑指数，在化学中有着许多的应用。本文采用分析结构的方法，对剖分双冠图、Q图双冠图、R图双冠图、T图双冠图的Zagreb指数进行了研究，给出了四类双冠图Zagreb指数计算公式。

冠图；Zagreb指数；图的运算；计算公式

本文所考虑的图是简单图(无环无多重边)。G表示顶点集为V(G)，边集为E(G)的图。dG(v)为图G中顶点v的度数，即与v相关联的边的数目。Zagreb指数是Gutman和Trinajstic在上个世纪七十年代(见文献[10,11])提出，是化学图论中的重要拓扑指数之一，在化学中有重要的应用。关于图G的第一类Zagreb指数M1(G)和第二类Zagreb指数M2(G)分别定义如下[2]：

M1(G)=∑u∈V(G)dG(u)2，

M2(G)=∑uv∈E(G)dG(u)dG(v)

第一类Zagreb指数M1(G)也可变形为

M1(G)=∑uv∈E(G)(dG(u)+dG(v))

在文献[8,13,15,19]中，Guntman等介绍了Zagreb指数的历史背景、发展历程、计算技巧和数学性质，关于Zagreb指数的研究结果主要见文献[1,4,9,12,14,18,19]。图G的线图L(G)=(V′,E′)，L(G)的顶点集V′一一对应与G的边集，L(G)中两个顶点邻接当且仅当两点对应的边在G中有公共端点。本文中，我们主要采用分析结构的方法，给出了剖分双冠图、Q图双冠图、R图双冠图、T图双冠图四类双冠图Zagreb指数计算公式。下面先介绍相关图的一些基本运算概念。

定义1[7]设G1和G2为顶点数为n1，n2，边数为m1，m2的简单图。冠图G1∘G2是由图G1、G2合成的图，其中使图G1的每一顶点分别与图G2的一个拷贝的所有顶点相连。(如图1所示)。

图1 冠图G1∘G2Fig.1 Corona graph G1∘G2

定义2[5,6]对于连通图G，定义四种相关的图如下：

图2 S(P3),R(P3),Q(P3),T(P3)Fig.2 S(P3),R(P3),Q(P3),T(P3)

(a)对图G的每一条边e，插入一个新点，即用长为2的路来代替边e得到的图，称为G的剖分图，记为S(G)。

(b)给定一个图G，对G的每一条边增加一个新点，新点与对应边的两个端点连线，所得的图记为R(G)。

(c)在G的每一条边插入一个新点，用一条长为2的路代替G中的边，“老”点互补邻接，两个新点在Q(G)中邻接当且仅当“新”点对应G中的边是邻接的，所得的图记为Q(G)。

(d)图G的全图，记为T(G)，它的顶点集是G的点集和边集的并集。T(G)中两点邻接当且仅当它们在G中相应的元素是邻接或关联。

其中，图S(G)和T(G)分别称为的剖分图和整图,更多运算的细节见文献[16]。为了方便运算，我们定义

F(G)∈{S(G),R(G),Q(G),T(G)}。

若图G是P3,则S(P3),R(P3),Q(P3),T(P3),如图2所示。

定义3[3]设G、G1和G2分别为顶点数为n,n1,n2,边数为q,q1,q2的连通图，四类双冠图：GF∘{G1,G2}是由图F(G),G1,G2合成的，其中使图F(G)的每一个旧的顶点分别与图G1的一个拷贝的所有顶点相连，使图F(G)的每一个新的顶点分别与图G2的一个拷贝的所有顶点相连。

图3 剖分双冠图Q图双冠图R图双冠图T图双冠图Fig.3 Subdivision double corona,Q-graph double corona,R-graph double corona and total double corona

1 第一类Zagreb指数和第二类Zagreb指数

首先，我们先研究图G(F)∘{G1,G2}的第一类Zagreb指数的计算公式。

表1 G(F)∘{G1,G2}的各类顶点的度

定理1 设G、G1和G2分别为顶点数为n,n1,n2,边数为q,q1,q2的连通图，则

(1)M1(G(S)∘{G1,G2})=

(2)M1(G(R)∘{G1,G2})=

(3)M1(G(Q)∘{G1,G2})=

A+M1(L(G))+(5+2n2)M1(G)+

(4)M1(G(T)∘{G1,G2})=

A+M1(L(G))+(8+2n2)M1(G)+

其中

A=nM1(G1)+qM1(G2)+n(4q1+n1)+q(4q2+n2)。

证明：令d(v)=dG(F)∘{G1,G2}(v)。

M1(G(F)°{G1,G2})=

∑v∈V(G(F)°{G1,G2})d(v)2=

(1)

(1)当i=1时，则v∈V1。由表1可知，

∑v∈V1(dG1(v)+1)2=∑v∈V1dG1(v)2+∑v∈V12dG1(v)+∑v∈V11=

M1(G1)+4q1+n1。

(2)当i=2时，则v∈V2。计算与(1)类似，则有：

得到

A=nM1(G1)+qM1(G2)+n(4q1+n1)+q(4q2+n2)。

(3)当i=3时，则v∈V3。

若F(G)∈{S(G),Q(G)}，由表1，有

d(v)=dG(v)+n1，则有：

∑v∈V3(dG(v)+n1)2=

∑v∈V3dG(v)2+∑v∈V32n1dG(v)+

若F(G)∈{R(G),T(G)}，由表1，有

d(v)=2dG(v)+n1，则有：

∑v∈V3(2dG(v)+n1)2=

(4)当i=4时，则v∈V4。

若F(G)∈{S(G),R(G)}，由表1，有

d(v)=2+n2，则有

若F(G)∈{Q(G),T(G)}，由表1，有

M1(L(G))+q(2+n2)2+

M1(L(G))+q(2+n2)2+

2(2+n2)(M1(G)-2q)。

(1)M1(G(S)∘{G1,G2})=

(2)M1(G(R)∘{G1,G2})=

(3)M1(G(Q)∘{G1,G2})=

A+M1(L(G))+(5+2n2)M1(G)+4qn1+

(4)M1(G(T)∘{G1,G2})=

A+M1(L(G))+(8+2n2)M1(G)+

接下来我们考虑图G(F)∘{G1,G2}的第二类Zagreb指数的计算公式。

首先根据图的结构，我们可以把图G(F)∘{G1,G2}的边分成七个子集

Ei(i=1,2,3,4,5,6,7)：

E1={e=uv,e∈E(G1)},

E2={e=uv,e∈E(G2)},

E3={e=uv,u∈V3,v∈V1},

E4={e=uv,u∈V4,v∈V2},

E5={e=uv,u∈V3,v∈V4},

E6={e=uv,u∈V3,v∈V3},

E7={e=uv,u∈V4,v∈V4}。

Ei(i=1,2,3,4,5,6,7)的数目由表2给出，其中

引理2 设图G是顶点数为n,边数为q的连通图，则

(1)M2(S(G))=2M1(G)；

(2)M2(R(G))=4M1(G)+4M2(G)；

(3)M2(Q(G))=M2(L(G))+

4M1(L(G))+10M1(G)-12q；

表2 图G(F)∘{G1,G2}的边子集的边的数目

(4)M2(T(G))=4M2(G)+M2(L(G))+4M1(L(G))+10M1(G)-12q。

证明根据S(G),R(G),Q(G),T(G)四类图中边的类型和各顶点的度，有：

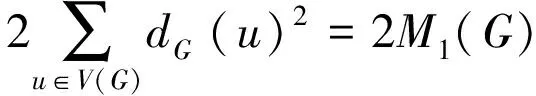
4M1(G)+4M2(G)；

4M2(G)+M2(L(G))+4M1(L(G))+

10M1(G)-12q；

M2(L(G))+4M1(L(G))+10M1(G)-12q。

定理3 设G、G1和G2分别为顶点数为n,n1,n2,边数为q,q1,q2的连通图，且图G(F)∘{G1,G2}的边的所有类型是Ei(i=1,2,3,4,5,6,7)，则

(1)M2(G(S)∘{G1,G2})=B+(2+n2)M1(G)+(2q+nn1)(2q1+n1)+q(2+n2)(2q2+n2)+2qn1(2+n2)；

(2)M2(G(R)∘{G1,G2})=

B+(2n2+2n1+4)M1(G)+

4M2(G)+(4q+nn1)(2q1+n1)+

(3)M2(G(Q)∘{G1,G2})=

B+M2(L(G))+(2q2+n1+4n2+

(2q+nn1)(2q1+n1)+q(2n2q2+

2n1(1+n2)-4n2-12)；

(4)M2(G(T)∘{G1,G2})=

10)M1(G)+(n2+4)M1(L(G))+

其中

B=nM1(G1)+nM2(G1)+qM1(G2)+

qM2(G2)+nq1+qq2。

证明记G′=G(F)∘{G1,G2}，

令d(v)=dG′(v)。为了方便计算，我们将G′的边集分成七个边子集Ei(i=1,2,…,7)，因此有

M2(G′)=∑e=uv∈E(G′)d(u)d(v)=

(2)

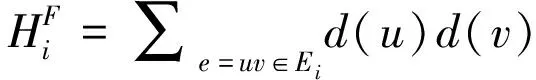
(1)当i=1时，则边e=uv∈E1。可得

∑e=uv∈E1(dG1(u)+1)(dG1(v)+1)=

∑e=uv∈E1dG1(u)dG1(v)+

∑e=uv∈E1(dG1(u)+dG1(v))+

∑e=uv∈E11=M1(G1)+M2(G1)+q1；

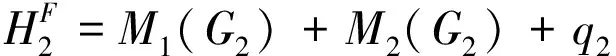
得到B=nM1(G1)+nM2(G1)+qM1(G2)+qM2(G2)+nq1+qq2；

(3)当i=3时，则边e=uv∈E3。由表1 和表2，可知

(4)当i=4时，则边e=uv∈E4。由表1 和表2，可知

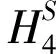
(5)当i=5时，则边e=uv∈E5。由表1 和表2，可知

(6)当i=6时，则边e=uv∈E6。由表1 和表2，可知

(7)当i=7时，则边e=uv∈E7。由表1 和表2，可知

∑e=uv∈E7(dL(G)(u)+2)(dL(G)(v)+2)+

(1)M2(G(S)∘{G1,G2})=

B+(2+n2)M1(G)+(2q+nn1)(2q1+n1)+

q(2+n2)(2q2+n2)+2qn1(2+n2)；

(2)M2(G(R)∘{G1,G2})=

B+(2n2+2n1+4)M1(G)+4M2(G)+

(4q+nn1)(2q1+n1)+q(2+n2)(2n1+

(3)M2(G(Q)∘{G1,G2})=

B+M2(L(G))+(2q2+n1+4n2+

(2q+nn1)(2q1+n1)+q(2n2q2+

2n1(1+n2)-4n2-12)；

(4)M2(G(T)∘{G1,G2})=

10)M1(G)+(n2+4)M1(L(G))+

M2(L(G))+(4q+nn1)(2q1+n1)+

其中B=nM1(G1)+nM2(G1)+qM1(G2)+

qM2(G2)+nq1+qq2。

[1]ASHRAFI AR,HAMZEH A,HOSSEIN.ZADEH S.Computing Zagreb,Hyper-Wiener and Degree-Distance indices of four new sums of graphs[J].Carpathian Journal of Mathematics,2011,27(2):153-164.

[2]BALABAN A T,MOTOC I,BONCHEV D,et al.Topological indices for structure-activity Correlations[M].Berlin：Springer,1983.

[3]BARIK S,SAHOO G.On the Laplacian spectra of some variants of corona[J].Linear Algebra & Its Applications,2016,512:32-47.

[4]KINKAR C,GUTMAN I.Some properties of the second Zagreb index[J].Match Communications in Mathematical & in Computer Chemistry,2004,52(52):103-112.

[5]DENG H,SARALA D,AYYASWAMY S K,et al.The Zagreb indices of four operations on graphs[J].Applied Mathematics & Computation,2016,275:422-431.

[6]ELIASI M,TAERI B.Four new sums of graphs and their Wiener indices[J].Discrete Applied Mathematics,2009,157(4):794-803.

[7]FRUCHT R,HARARY F.On the corona of two graphs[J].Aequationes mathematicae,1970,4(1-2):264-264.

[8]GUTMAN I,DAS K C.The first Zagreb index 30 years after[J].Match Communications in Mathematical & in Computer Chemistry,2004,50(50):83-92.

[9]GUTMAN I,GOUBKO M V.Trees with fixed number of pendent vertices with minimal first Zagreb Index[J].Bull.Int.Math.Virt.Inst.2013,3:161-164.

[10]GUTMAN I,RUIC B,TRINAJSTIC N,et al.Graph theory and molecular orbitals.XII.Acyclic polyenes[J].Journal of Chemical Physics,1975,62(9):3399-3405.

[11]GUTMAN I,TRINAJSTIC N.Graph theory and molecular orbitals.Total φ-electron energy of alternant hydrocarbons[J].Chemical Physics Letters,1972,17(4):535-538.

[12]GOUBKOM,RETIT.Minimizing degree-based topological indices for trees with given number of pendent vertices[J].MATCH Commun.Math.Comput.Chem,2014,71:33-46.

[13]KHALIFEH M H,YOUSEFI-AZARI H,ASHRAFI A R.The first and second Zagreb indices of some graph operations[J].DiscreteApplied Mathematics,2009,157(4):804-811.

[14]LIN H.On Segments,Vertices of Degree Two and the First Zagreb Index of Trees[J].Match Communications in Mathematical & in Computer Chemistry,2014,72(3):825-834.

[15]NIKOLICS,KOVACEVIC G,.MILICEVIC A,et al.The Zagreb Indices 30 Years After[J].CroaticaChemica Acta,2003,76(2):113-124.

[16]SAVAGE G J,TOIDA S.Spectra of graphs:theory and application[J].Journal of the Franklin Institute,1981,311(6):403.

[17]VELUSAMY AK,IYER R R.Zagreb Indices of the Total Graphs of Graphs[J].Journal of Applied Sciences Research,2016,3:59-64.

[18]YARAHMADI Z,ASHRAFI A R.The Szeged,vertex PI,first and second Zagreb indices of corona product of graphs[J].Filomat,2012,3(3):467-472.

[19]ZHOU B,GUTMAN I.Further properties of Zagreb indices[J].Match Communications in Mathematical & in Computer Chemistry,2005,54(1):233-239.

On Zagreb indices of some variants of corona

WANG Dijian，XIAO Xiangfeng，TANG Zikai

(College of Mathematics and Computer Science，Hunan Normal University，Changsha 410081，China)

Let G=(V,E)be a simple graph with vertex set V and edge set E.The Zagreb indices are one of the important chemical topological indices,which have a lot of applications in chemistry.In this paper,we give the computational formulas of the Zagreb indices for subdivision double corona,Q-graph double corona,R-graph double corona and total double corona by analyzing graph structures.

corona；Zagreb indices；operation on graphs；computational formulas

1672-7010(2017)04-0011-08

2017-03-18

湖南师范大学优秀青年基金资助项目(ET13101)

王狄建(1993-)，男，浙江绍兴人，硕士，主要从事图论及其应用研究;E-mail:827674326@qq.com

汤自凯(1973-)，男，湖南宁乡人，副教授，博士，主要从事图论及其应用研究;E-mail:zikaitang@163.com

O157.5

A